H-循环矩阵线性系统求解及其求逆的多项式快速算法
何承源,张坤鹏*,马江明
(西华大学 理学院,成都 610039)
1 引言及预备知识
由于循环矩阵在信号处理、数字图像处理、编码理论、自回归分析等领域的广泛应用,因此关于循环矩阵线性系统的求解问题十分重要[1-4],但其求解过程需要计算大量的三角函数,存在误差且影响效率。利用循环矩阵与多项式的关系,本文引进多项式快速算法,以克服文献[1-4]中算法的缺陷。本文针对H-循环矩阵[5]给出多项式快速算法,它仅利用H-循环矩阵的第一行元素进行计算,因此在理论上是精确的。该算法有一个显著特点,求解时不需要预先知道H-循环矩阵是非奇异还是奇异。
定义1[5]如果矩阵A具有如下形状

则称A为 H-循环矩阵,简记为 A=Hcirc(a0,a1,…,an-1)。
定义2 设A∈Cn×n,如果B∈Cn×n满足1)ABA=A;2)BAB=B,则称B为A的自反g逆,简记为A{1,2}。
引理1[5]A为H-循环矩阵的充要条件是A=f(π)。这里f(x)=a0+a1x+… +an-1xn-1为H-循环矩阵A的表示多项式(下同)。
引理 2[5]n 阶矩阵 π =Hcirc(0,1,0,…,0)称为基本H-循环矩阵。知易πn=I-π,g(x)=xn+x-1为π的特征多项式(下同)。
引理3[5]n阶H-循环矩阵A非奇异的充要条件是(f(x),g(x))=1。
引理4 g(x)=xn+x-1的根是n个单根。
引理5[6]若多项式矩阵经初等行变换化为,则(f(x),g(x))=d(x)且满足f(x)u(x)+g(x)v(x)=d(x)。
2 主要结论
定理1 若n阶非奇异H-循环矩阵A=Hcirc(a0,a1,…,an-1),b=(b0,b1,…,bn-1)T,则存在唯一的 n 阶 H-循环矩阵 C=Hcirc(c0,c1,…,cn-1)使得AX=b的唯一解X是C的第1列,即X=Hcirc(c0,cn-1,…,c2,c1)T。
证明 因为矩阵A=Hcirc(a0,a1,…,an-1)非奇异,所以由引理3,有(f(x),g(x))=1。由 b=(b0,b1,…,bn-1)T构造 B=Hcirc(b0,bn-1,bn-2,…,b1),则B的表示多项式为,从而由引理5对多项式矩阵只进行一系列行初等变换一定能化为,于是
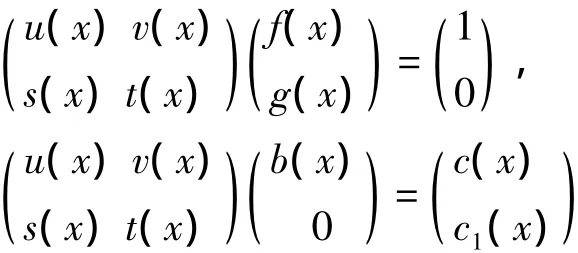
即 f(x)u(x)+g(x)v(x)=1,u(x)b(x)=c(x),在上式中,令 x=π,则 f(π)=A,g(π)=0,B=b(π),于是:

因此由(1)知u(π)是A的唯一逆矩阵A-1。从而由矩阵相乘的意义和H-循环矩阵的特点知H-循环矩阵 C=Hcirc(c0,c1,…,cn-1)=c(π)=A-1B 的第1 列是(c0,cn-1,…,c2,c1)T=A-1b。因为 AA-1b=b,所以 X=A-1b=(c0,cn-1,…,c2,c1)T是 AX=b 的解。
又因为H-循环矩阵A-1和B均是唯一的,所以A-1B 也是唯一的,于是 X=A-1b=(c0,cn-1,…,c2,c1)T也是唯一的。
推论2 若n阶非奇异H-循环矩阵A=Hcirc(a0,a1,…,an-1),则 A 的逆矩阵 A-1=u(π)=Hcirc(c0,c1,…,cn-1)。
定理3 若n阶奇异H-循环矩阵A=Hcirc(a0,a1,…,an-1),b=(b0,b1,…,bn-1)T,线性方程组 AX=b有解,则存在唯一的 H-循环矩阵 C=Hcirc(c0,c1,…,cn-1)的第1 列 X1=(c0,cn-1,…,c2,c1)T是 AX=b的唯一特解和 M=Hcirc(m0,m1,…,mn-1)使得 X2=X1+(In-M)Z是AX=b的通解。这里Z是任意的n维列向量。
证明 因为 A=Hcirc(a0,a1,…,an-1)是奇异的,所以由引理3的逆否命题和引理5,对多项式矩阵只进行一系列行初等变换一定能化为这里d(x)是f(x)和g(x)不等于1的最大公因式。
若设 f(x)=d(x)f1(x),g(x)=d(x)g1(x),则(f1(x),g1(x))=1。
因为由引理4知g(x)=xn+x-1的根是n个单根,所以(d(x)g1(x))=1,(f(x),g1(x))=(d(x)f1(x)),g1(x))=1,(f(x)d(x),g1(x))=1。
由 b=(b0,b1,…,bn-1)T构造 H-循环矩阵 B=Hcirc(b0,bn-1,bn-2,…,b1),则 B 的表示多项式为,从而由引理5对多项式矩阵

在(3)式两端乘以f(x),得

在式(4—6)中,令x=π,则f(π)=A,g(π)=0,B=b(π),于是

同理,在式(3)两端同乘以d(x)u(x)且令x=π,得

由式(9—10)知 H-循环矩阵 R=d(π)u(π)是A 的自反 g 逆。令 C=c(π)=RB=Hcirc(c0,c1,…,cn-1),M=m(π)=RA=Hcirc(m0,m1,…,mn-1)。对RB=C,根据矩阵相乘的意义和H-循环矩阵B的特点知 H-循环矩阵 C 的第 1 列是(c0,cn-1,…,c2,c1)T=Rb。
因为AX=b有解,所以ARb=b,这说明列向量Rb是AX=b的一个解。
因为 A[Rb+(In-M)Z]=ARb+A(In-N)Z=b,所以X2=X1+(In-M)Z是AX=b的通解,其中Z为任意的n维列向量,X1=Tb。
因为A,R均是H-循环矩阵,所以AR=RA。同时也易知Rb是唯一的。
推论4 若n阶奇异H-循环矩阵A=Hcirc(a0,a1,…,an-1),则H-循环矩阵A的自反广义逆矩阵是H-循环矩阵 A{1,2}=d(π)u(π)。
3 算法及数值算例
由定理1和2很容易得到H-循环矩阵A的求逆矩阵和线性系统AX=b求解的多项式快速算法,其步骤如下:
1)由H-循环矩阵A和AX=b得到多项式f(x),g(x),b(x)。
3)如果d(x)=1,则H-循环矩阵A非奇异和线性系统AX=b有唯一解。对多项式u(x)和c(x),令x=π,则H-循环矩阵A的逆矩阵A-1=u(π)和C=c(π)=Hcirc(c0,c1,…,cn-1)的第 1 列(c0,cn-1,…,c2,c1)T是 AX=b的唯一解。
4)如果d(x)≠1,那么用d(x)去除g(x)得商式g1(x),对多项式矩阵

5)对于多项式 p(x),令 x=π,则 P=p(π)=AA{1,2}B。于是若H-循环矩阵P的第1列就是n维列向量b,则H-循环矩阵线性系统AX=b有解,否则无解。因此,对于多项式c(x),m(x),若令x=π,则H-循环矩阵 C=c(π)=A{1,2}B,M=m(π)=A{1,2}A。故H-循环矩阵C的第1列就是AX=b的唯一特解,设为X1,则X2=X1+(In-M)Z是AX=b的通解,其中Z为任意n维列向量。同时,H-循环矩阵A的广义逆矩阵是 H-循环矩阵 A{1,2}=d(π)u(π)。
例 1 设 A=Hcirc(1,1,1,1),试求:1)解线性方程组 AX=b,这里 b=(1,2,3,4)T;2)A=Hcirc(1,1,1,1)的逆矩阵。
解 因为 H-循环矩阵 A=Hcirc(1,1,1,1),所以f(x)=1+x+x2+x3,g(x)=x4+x-1。
因为 b=(1,2,3,4)T,所以 b(x)=1+4x+3x2+2x3。因此对下列多项式矩阵作一系列行初等变换化为:

则c(x)=x3+4x4+3x5+2x6,u(x)=x3因为 π4=I-π,所以 c(π)=Hcirc(4,-1,-1,-1),u(π)=Hcirc(0,0,0,1),故 X=A-1b=(4,-1,-1,-1),A-1=Hcirc(0,0,0,1)。


构造多项式矩阵并进行行初等变换:

C,k2∈C)。同时,H-循环矩阵的广义逆矩阵是H-循环矩阵
[1]GOHBERG I,KAILATH T,KOLTRACHT I,et al.Linear complexity parallel algorithms for linear systems of equations with recursive structure[J].Linear Algebra & Its Applications,1987(3):271 –315.
[2]FRANK D H.A new algorithm for solving Toeplitz systems of equations[J].Linear Algebra & Its Applications,1987(88-89):123–138.
[3]LIZER E.On the stability of transform-based circular deconvolution[J].Siam Journal on Numerical Analysis,1992,29(5):1482-1492.
[4]CHEN M K.On the Solution of Circulant Linear Systems[J].Siam Journal on Numerical Analysis,1987,24(3):668-683.
[5]HE C Y,WANG X Y.The discriminance for a special class of circulantmatrices and their diagonalization[J]. Applied Mathematics& Computation,2014,238(7):7–12.
[6]张晓红,蔡秉衡.高等代数专题研究选编[M].西安:西安科学技术出版社,1992.

