土质边坡稳定影响因素的敏感性分析

钟学梅，付成华*，何 欢，赵 川

(西华大学 能源与动力工程学院，成都 610039)

边坡稳定性是岩土工程领域里一个重要的研究课题［1］。随着计算机技术的发展，边坡稳定性分析方法已经从定性分析法(经验类比法、工程地质法、结构分析法)发展到现在的定量分析方法(极限平衡法、数值计算方法)。但由于边坡稳定性受地形、地貌、地质构造、边坡坡度、地下水、坡顶作用荷载、降雨入渗、软弱夹层等因素的影响，其中有些因素又具有随机性、可变性等特点，使得边坡的稳定性具有不确定性［2-5］，所以在采用极限平衡法和数值计算方法对边坡进行定量分析的基础上，还应用不确定分析法(敏感性分析、可靠性分析、灰色系统预测法、人工智能等)对不同的影响因素进行分析，从而更准确地分析边坡的稳定性，预防滑坡等问题。

目前许多学者对边坡稳定性的影响因素进行敏感性分析［4］。倪恒等［5］认为敏感性分析的一般方法具有局限性，于是采用正交设计方法，对地震力加速度、内摩擦角、粘聚力、岩体密度和水位变化进行敏感性分析，利用SARMA法计算稳定性系数，并利用方差分析法对试验结果进行处理，从而得出水位变化为最敏感因素;曹军义等［6］以非饱和土含水率为影响因素计算了不同含水率下边坡的安全系数，从而确定了含水率是影响边坡稳定的一个重要参数;吕晓光等［7］采用正交试验法分析土的不饱和重度、渗透系数、弹性模量、泊松比、粘聚力和内摩擦角对边坡稳定性的影响，运用极差分析法处理试验结果，从而得出内摩擦角对边坡稳定的影响性最大。本文在此基础上，考虑边坡土容重、粘聚力、内摩擦角、地下水位以及坡比等5个影响因素，分别采用单因素分析法和正交试验法进行敏感性分析，利用极限平衡法中的Morgenstern-price法计算不同因素条件下的边坡稳定安全系数，并以此作为试验指标，利用极差分析法［7］分析其变化规律，根据安全系数的变化幅度，确定各因素影响程度、敏感性大小。同时，通过对比单因素分析法和正交试验法的分析，进一步探讨2种分析方法的优缺点。

1 单因素法进行敏感性分析

单因素分析法是一种比较简单的、用于分析影响因素敏感性大小的方法［4］。边坡稳定性影响因素的敏感性分析常将稳定安全系数K作为试验指标，K与影响因素Xi之间的函数关系可表示为:K=f(X1，X2，…，Xn)。

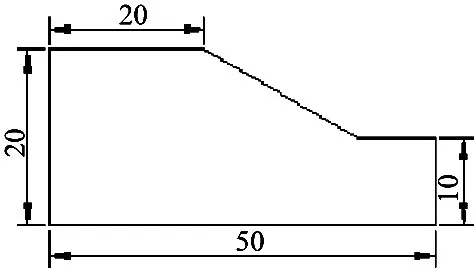
图1 均质边坡剖面

以图1所示的均质土质边坡为例，单因素敏感性的分析步骤为:

1)选定基准值坡高10 m，坡顶距左边界20 m，坡脚距右边界10 m，坡比为1∶2，粘聚力14 kPa，土容重18 kN·m-3，内摩擦角 20°，不考虑地下水，计算出K。

2)分别改变土容重、粘聚力、内摩擦角、地下水位及坡比，利用geo-slope软件，采用极限平衡法中的Morgenstern-price法［1］计算不同因素条件下的K。

3)分别计算出K的相对变化率和各因素的相对变化率，其比值即为各因素的敏感度，其中:为K的相对变化率;为各因素的相对变化率。

单因素敏感性分析结果如表1—6所示。

表1 重度敏感性分析

由表1可知:随着土容重的增加，K呈减小趋势。

表2 粘聚力敏感性分析

由表2可知:粘聚力越大，K越大。

表3 内摩擦角敏感性分析

由表3可知:K随着内摩擦角的增大而增大。

表4 地下水敏感性分析

由表4可知:地下水位越低越有利于边坡稳定。

表5 坡比敏感性分析

由表5可知:随着坡比的增大，K越来越大，越有利于边坡的稳定。

综合计算出这5个因素的敏感度如表6所示，可见:边坡坡比的敏感度最大，其次是土体的内摩擦角、粘聚力、土容重，最不敏感的因素是地下水位。

表6 敏感度计算结果

2 多因素正交试验法进行敏感性分析

表7 因素水平表

2)根据正交试验原则和特点，选择合适的正交

多因素分析法考虑了各因素变化之间的相关性，能反应出各因素同时变化对边坡稳定性的影响。这里采用多因素分析法中的正交试验设计方法［7］来考虑多因素同时变化的相关性。

以图1所示的均质边坡为例，具体步骤为:

1)考虑土容重、粘聚力、内摩擦角、地下水位、坡比5个因素对边坡稳定性的影响，采用5因素3水平进行正交试验，因素水平如表7所示。表Lm(ar)，其中:L为正交表符号;m为试验次数;a为因素的水平数;r为正交表列数。这里有5因素3水平，故选用L18(35)，确定正交试验方案。

3)利用geo-slope软件，采用极限平衡法中的Morgenstern-price法计算不同试验方案下的边坡稳定安全系数。

4)以稳定安全系数作为考察指标，对试验结果进行极差分析［7］，确定这些影响因素的敏感度。

正交试验方案及稳定安全系数计算结果如表8所示。

表8 正交试验方案及计算结果

由正交试验设计方案计算得到的边坡最大安全系数为2.386，对应方案3:土容重取最小值，粘聚力和内摩擦角取最大值，地下水位取最低水位，坡比取最大值，即边坡坡度越缓、土体的粘聚力和内摩擦角越大、地下水位越低、土容重越小，越有利于边坡的稳定。

根据表8的计算结果，求出各个因素相同水平下的平均值，用最大值减去最小值得到极差，极差分析结果如表9所示。由极差分析结果可知，边坡稳定的这5个影响因素中敏感性由强到弱分别为坡比、内摩擦角、粘聚力、土容重和地下水位。

表9 极差分析表

3 结语

采用极限平衡法对土容重、粘聚力、内摩擦角、地下水位以及边坡的坡比进行了单因素和多因素敏感性分析表明:单因素分析法单独考虑各个影响因素的变化，没有考虑因素间的相关性，试验结果具有局限性，不过单因素分析法能直观地反映单一因素对边坡稳定性的影响。正交试验法考虑了多因素间的相关性，试验结果更加准确，采用多因素正交试验法进行敏感性分析更合理。同时由敏感性分析确定出了影响边坡稳定性的主要因素和次要因素，即坡比的敏感性最强为主要影响因素，其次分别为土体的物理力学参数:内摩擦角、粘聚力、土容重，敏感性最小的是地下水位，这对土质边坡稳定和灾害防治有一定的参考价值。通常实际工程边坡的稳定性还受降雨、地震等因素的影响。影响因素越多，且这些因素之间相互影响、相互作用，实际情况将越复杂，因此，进一步深入研究边坡稳定影响因素的敏感性对实际工程边坡治理和灾害防治具有重要意义。

［1］陈祖煜.土质边坡稳定分析:原理·方法·程序［M］.北京:中国水利水电出版社，2005.

［2］曾亚武，田伟明.边坡稳定性分析的有限元法与极限平衡法的结合［J］.岩石力学与工程学报.2005，24(S2):5355-5359.

［3］郑颖人，陈祖煜，王恭先，等.边坡与滑坡工程治理［M］.北京:人民交通出版社，2007.

［4］何本贵，高谦，刘芳.公路路堑边坡稳定性影响因素正交分析与数值模拟［J］.岩土工程学报，2005，27(6):716-719.

［5］倪恒，刘佑荣，龙治国.正交设计在滑坡敏感性分析中的应用［J］.岩石力学与工程学报，2002，21(7):989-992.

［6］曹军义，展辰辉，王改山.土质高边坡稳定因素的敏感性分析［J］.岩石力学与工程学报，2005，24(S2):5350-5354.

［7］吕晓光，崔可锐，李丹，等.基于Plaxis的土质边坡稳定性影响因素分析［J］.安徽建筑工业学院学报，2010，18(3):67-71.