垂直均布荷载矩形基础地基任意点附加应力系数公式推导

石中平

（西安中交公路岩土工程有限责任公司，西安710075）

1 集中荷载附加应力公式

1885年，法国学者J.Boussinesq用弹性理论导出了半空间弹性体表面作用竖向集中力p时，在弹性体内任意点引起的全部6应力（σx，σy，σz，τxy，τyz，τxz）及全部3位移（ux，uy，uz）。在6个应力分量中有3个法向应力分量、3个剪应力分量。其中，对建筑工程地基沉降计算直接关联的是竖向法向应力分量σz（即附加应力）［1］，其公式如下

式中：x、y、z为计算点的坐标。

该式是推导地基附加应力系数公式的基础。

2 均布荷载矩形基础地基任意点附加应力系数公式

需要说明的是，由于推导过程繁琐、排版困难，本文仅给出一些必要的提示性步骤。

设坐标原点取在矩形基础任意角点处，矩形基础长度和宽度分别为l、b，并作用均布荷载p。在矩形基础中任意点（ξ，ζ）取一微面积dA＝dξ×dζ，此微面积上的作用力为dp＝pdA＝pdξ×dζ，并视其为集中力。在矩形基础以外任取一点（x，y），代入（1）式得微荷载dp＝pdξ×dζ作用下地基任意点（x，y）的微附加应力为

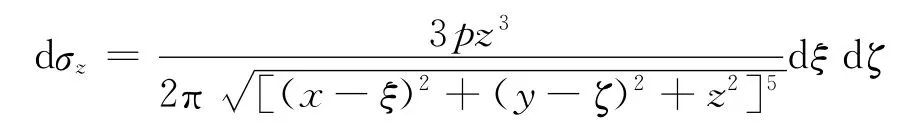
整个矩形基础均布荷载在该任意点（x，y）的附加应力即为对上式微附加应力的重积分

令X＝x－ξ、Y＝y－ζ，则dX＝－dξ、dY＝－dζ。代入上式得

此式与矩形基础均布荷载角点下地基附加应力公式相似，只是积分区间不同而已。

令＝X2＋z2，则上式变为

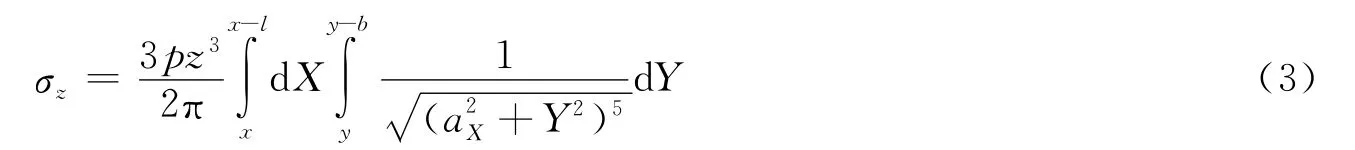
令Y＝aXtant，则dY＝aXsec2tdt，代人（3）式并整理得

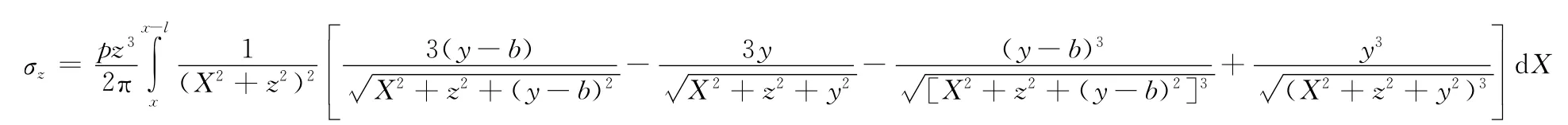
令X＝ztant，则dX＝zsec2tdt，代入上式整理后得

令η＝sint，则dη＝costdt，cos2t＝1－η2，代入上式整理后得

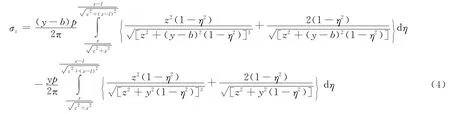
（4）式积分项可分解成如下4个积分

效仿上述过程，（4-1）式积分第2项变为

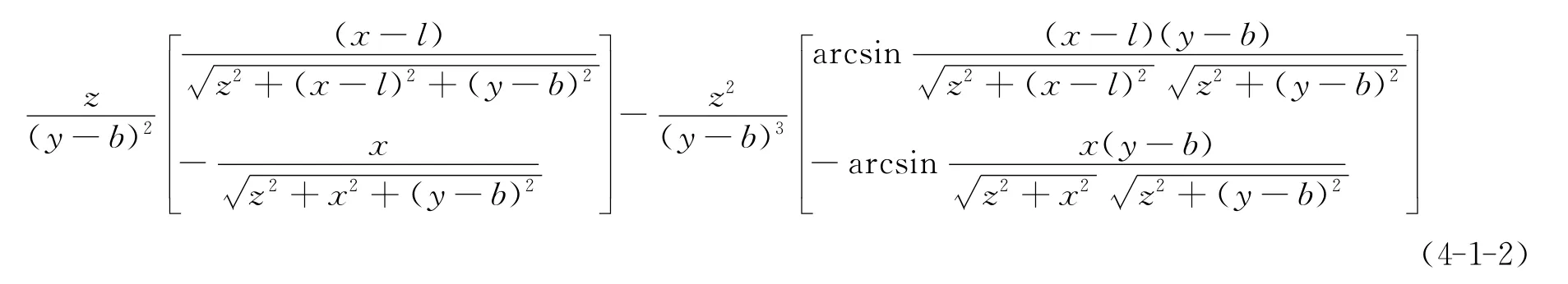
将（4-1-1）、（4-1-2）代入（4-1）式并简化整理后得

效仿上述过程，（4-2）式中积分第1项变为

（4-2）式中积分第2项变为

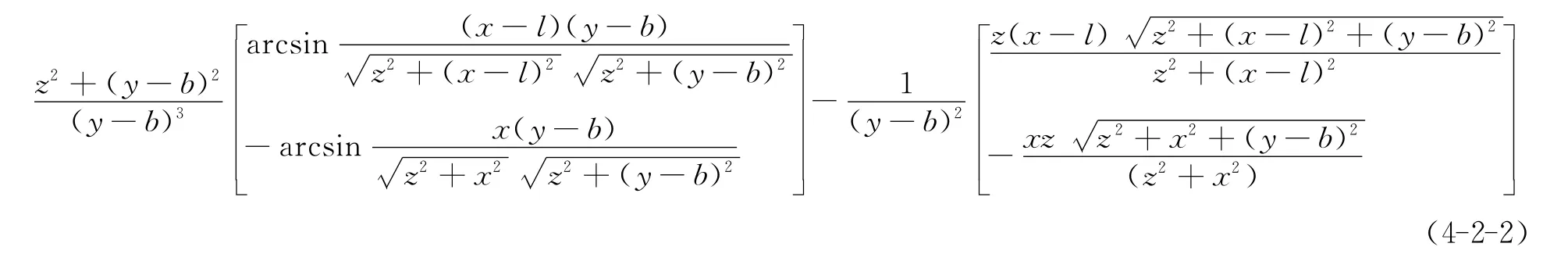
将（4-2-1）、（4-2-2）代入（4-2）式并简化整理得

效仿上述过程，（4-3）式中第2项积分变为

将（4-3-1）、（4-3-2）代入（4-3）式并化简整理得

效仿上述过程，（4-4）式中第1项积分变为

（4-4）式中第2项积分变为

将（4-4-1）、（4-4-2）代入（4-4）式并化简整理得

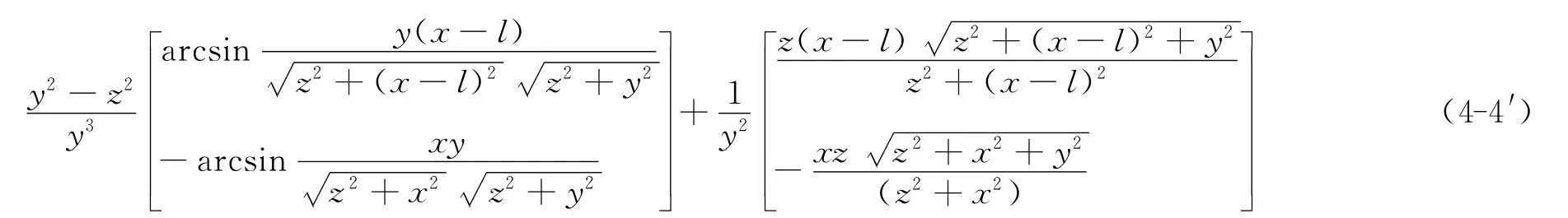
将（4-1′）、（4-2′）、（4-3′）、（4-4′）代入（4）式整理后即得矩形基础均布荷载下地基任意点附加应力公式

上述推导过程中，（2）式是先对y后对x的积分顺序。当然也可以采用先对x后对y的积分顺序，即如下积分形式

以下步骤与上述完全相同，不再列出，只要将上述公式中的（x－l）、（y－b）及x、y依次变为（yb）、（x－l）及y、x即可，公式如下

令

或

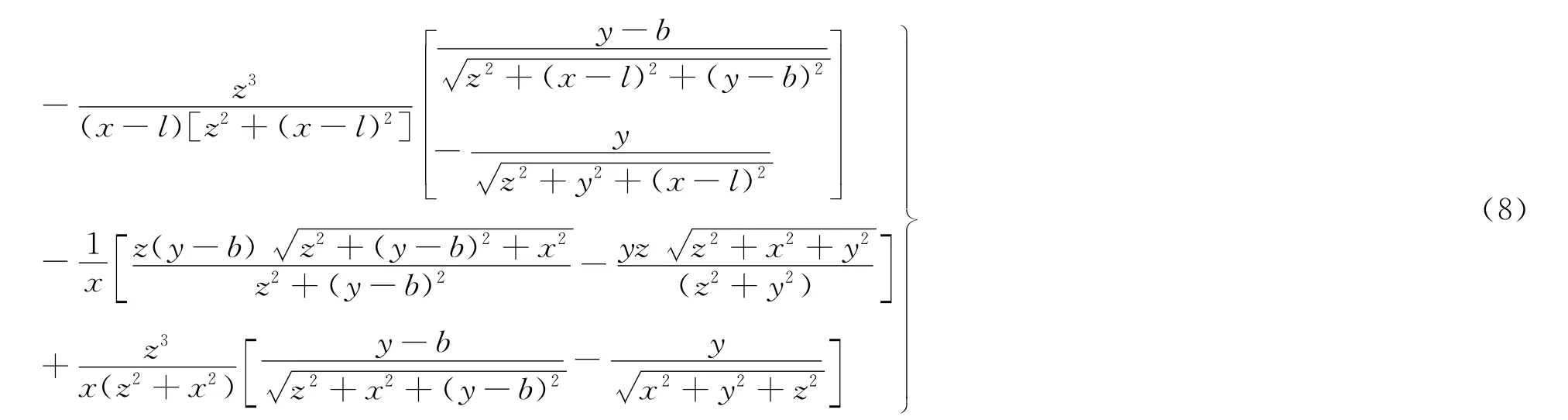
（7）、（8）式均为垂直荷载作用下矩形基础地基任意点附加应力系数公式。不难发现，2个式子中反正弦三角函数形式是完全一样的。将2个式子等号两侧对应项两两相加并整理后得到以下第3种垂直荷载作用下矩形基础地基任意点附加应力系数的公式

（7）、（8）、（9）式均为垂直荷载作用下矩形基础地基任意点附加应力系数计算公式，而（9）式是（7）、（8）式的综合，更具一般性。为了与有关书籍或规范中以反正切三角函数表示的附加应力系数计算公式对比，以（9）式为例将其转换为反正切三角函数形式。

由三角关系得

将（9-1）—（9-4）式带入（9）式即得以反正切三角函数表示的附加应力系数计算公式

3 公式验证

以下仅以（10）式为例，分别推求了一些特殊点，如角点、中点、长边中点及基础以外2l×2b区域角点4种具体情况下的计算公式，并对角点公式进行了对比。

3.1 特殊点下附加应力系数计算公式

3.1.1 角点

当x＝0、y＝0，x＝l、y＝0，x＝0、y＝b，x＝l、y＝b时，计算点位于4个角点正下方。分别将上述4种组合代入（10）式可得下列4个公式。需要注意的是，在将含有0的（x，y）代入（10）式时会出现分母为0的分式，此时，只要这些分式不参与计算，即作为0处理即可。至于为何会出现分母为0的分式，这是由于在积分推导过程中这些分式分母均以代数形式给出，并一直沿袭到最后的结果。

可见，上述4个式子具有完全相同的形式，说明4个角点的附加应力系数是一致的，进一步说明所推导公式是正确的。对上述4个式子进一步整理得

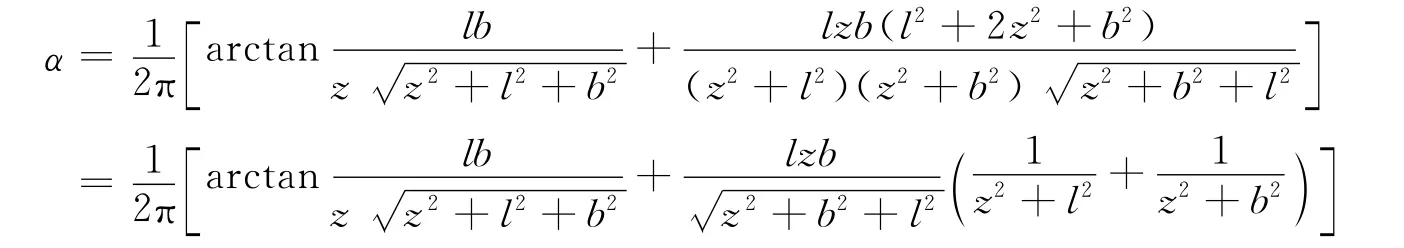
该式为以（l，b，z）表示的矩形基础均荷载角点附加应力系数计算公式。若令m＝l/b，n＝z/b，代入并整理即得（11）式以（m，n，z）表示的矩形基础均布荷载角点附加应力系数公式。该式与陈希哲［1］、龚文惠［2］中的公式完全一致。至于陈晋中［3］的公式，只要将其进行变换，就可得到与（11）式完全一致的形式，在此不再赘述。

3.1.2 中心点

当x＝0.5l、y＝0.5b时，计算点即位于矩形基础中点正下方。代入（10）式整理后得

该式为以（l，b，z）表示的矩形基础均荷载中点附加应力系数计算公式。显然，该式是某个矩形基础角点附加应力系数的4倍，该矩形基础就是将原矩形长宽各缩小至原大小的1/2所得的4个相同的小矩形。若令m＝l/b，n＝z/b，代入并整理后即为以（m，n，z）表示的矩形基础均布荷载中点附加应力系数计算公式。

3.1.3 边中点——以长边中点为例

当x＝0、0＜y＜b，x＝l、0＜y＜b，y＝0、0＜x＜l，y＝b、0＜x＜l时，计算点即位于矩形基础4个边点正下方。因过程一致，下面仅以长边中点为例进行验证，即将x＝0.5l、y＝0代入（10）式整理后得

此式为以（l，b，z）表示的矩形基础均荷载长边中点附加应力系数计算公式。显然，该式是某个矩形基础附加应力系数的2倍，该矩形基础就是原矩形宽度保持不变而长边缩小至原长度的1/2所得的2个相同小矩形。若令m＝l/b，n＝z/b，代入并整理后即为以（m，n，z）表示的矩形基础均布荷载长边中点附加应力系数计算公式。

3.1.4 基础范围以外任意点——以2l×2b区域角点为例

当x＞l、x＜0、y＞b、y＜0时，计算点即位于矩形基础外侧任意点正下方。下面仅以位于2l×2b区域角点为例进行验证。在此，即将x＝2l、y＝2b代入（10）式整理后得

仔细分析不难发现，上式4个方括号项其实就是2l×2b、l×b、2l×b、l×2b这4个矩形角点的附加应力系数公式，说明基础外任意点附加应力系数是上述4个矩形基础附加应力系数之代数和，即只要根据矩形均布荷载角点附加应力系数公式分别计算出2l×2b、l×2b、2l×b、l×b这4个矩形角点的附加应力系数后，再按照即可求得2l×2b区域角点下的附加应力系数。

上式为以（l，b，z）表示的均荷载作用下矩形基础外任意点附加应力系数计算公式。若令m＝l/b，n＝z/b，代入并整理后即为以（m，n，z）表示的均布荷载作用下矩形基础以外任意点附加应力系数计算公式。

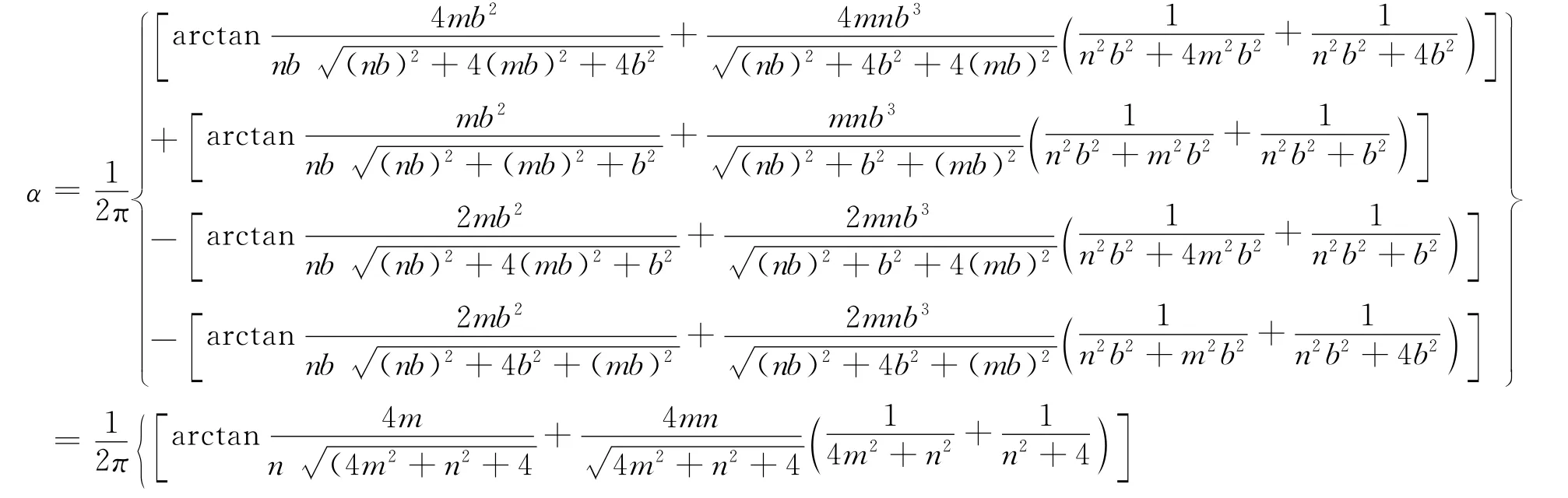
3.2 计算结果对照

为便于表述，本文将采用公式进行计算称为“公式法”。图1为《土力学地基基础》［1］例题3-1、《土力学》［2］例题4.2及《土力学与地基基础》［3］例题3-3的同一示例，要求荷载面积2m×1m、角点A、长边中点E、中心点O及荷载面以外F、G点下z＝1m处的附加应力系数。角点法的计算结果见表1。图2为《土力学》［2］例题4.3，3个基底大小和所受荷载完全相同的相邻矩形基础，基础净距为2m，要求基础甲中心O点深度2m处的地基附加应力。角点法的计算结果见表2。

从表1、表2明显看出，除完全一致的计算结果外，差别较大的0.082 2与0.081 4及0.747 7与0.746 4也仅仅相差0.000 8及0.001 3。前者由2.5×1.0 矩形引起（z＝1）：角点法数值0.201 6，公式法数值0.202 4，后者由2.5×2.0矩形引起（z＝2）：角点法数值0.186 6，公式法数值0.186 9，均由线性内插引起。

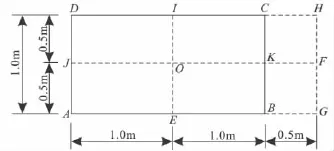
图1 角点法示意图（单个基础）Fig.1 The sketch map of the corner point method（a single foundation）

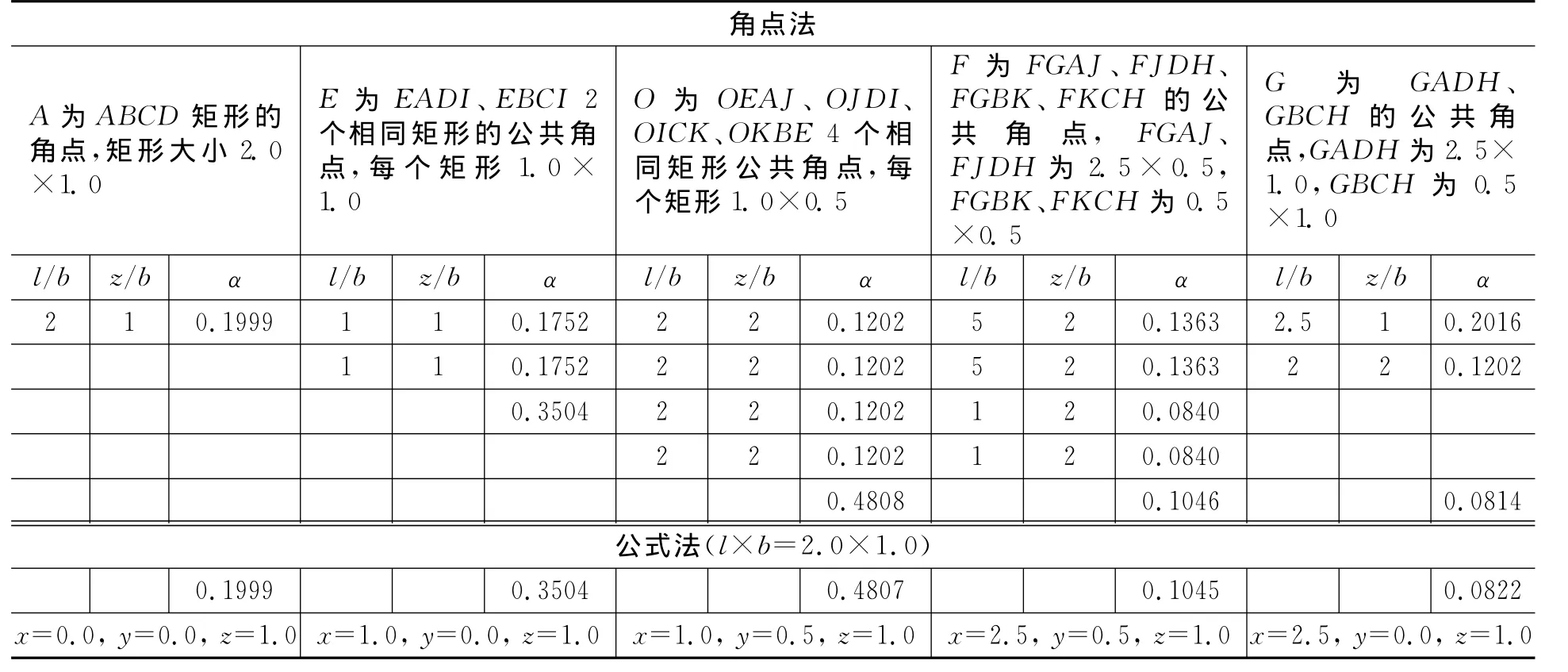
表1 角点法、公式法计算表（单个基础）Table 1 The calculated results by the corner point method and the formula method（a single foundation）

图2 角点法示意图（多个基础）Fig.2 The sketch map of the corner point method（multiple foundation）

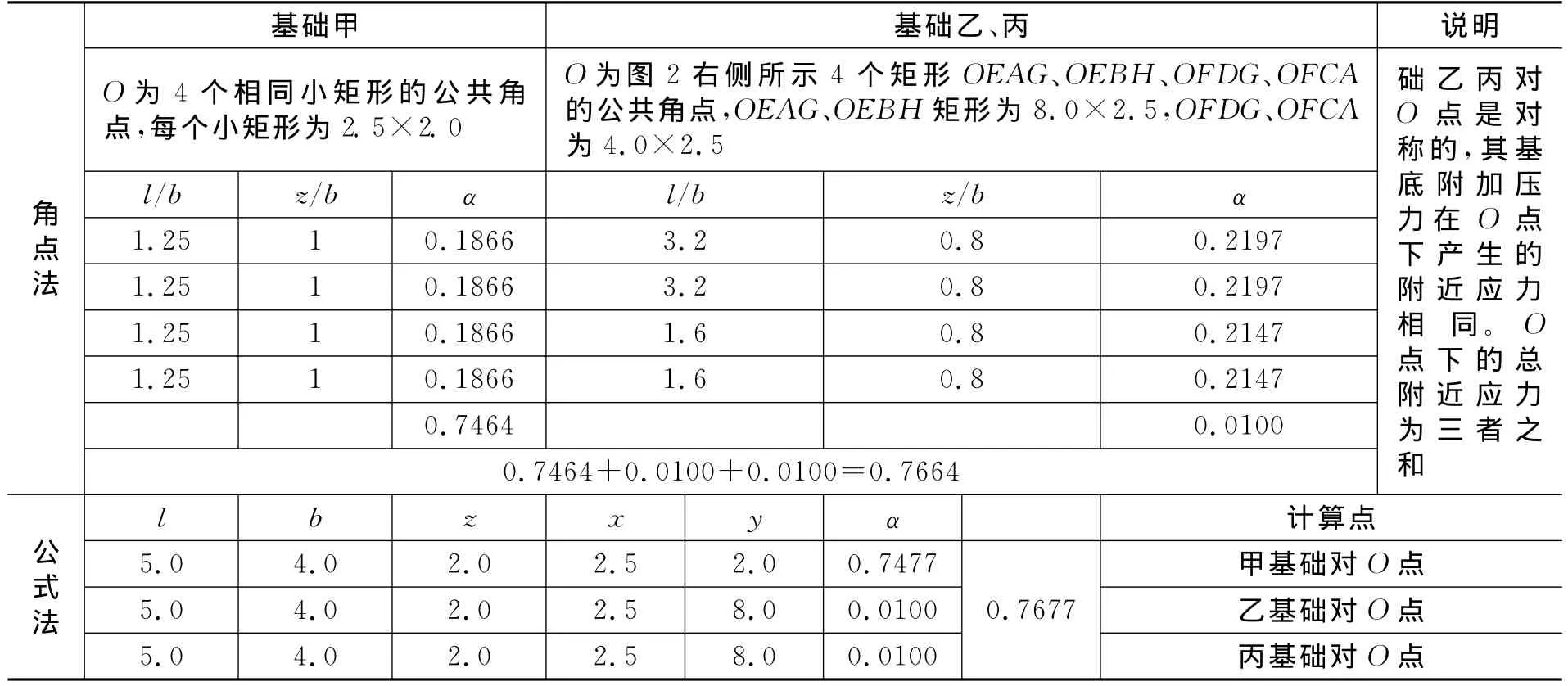
表2 角点法、公式法计算表（多个基础）Table 2 The calculated results by the corner point method and the formula method（multiple foundation）

表3为公式法与《土力学地基基础》表3-4角点法计算结果［4］对照表。明显看出，差别不超过±0.3‰。

4 结论

a.本文利用积分导出了垂直均布荷载作用下矩形基础地基中任意点附加应力系数的计算公式，虽然表达式复杂，不易记忆，但可借助Excel编制相应的计算程序，使得计算过程异常便利。

b.公式（10）更具一般性，据此导出了一些特殊点，如角点、中心点、边中点及2l×2b区域角点下具体的计算公式，并通过与有关文献所列角点下的计算公式对比，证明推导的公式是正确的。

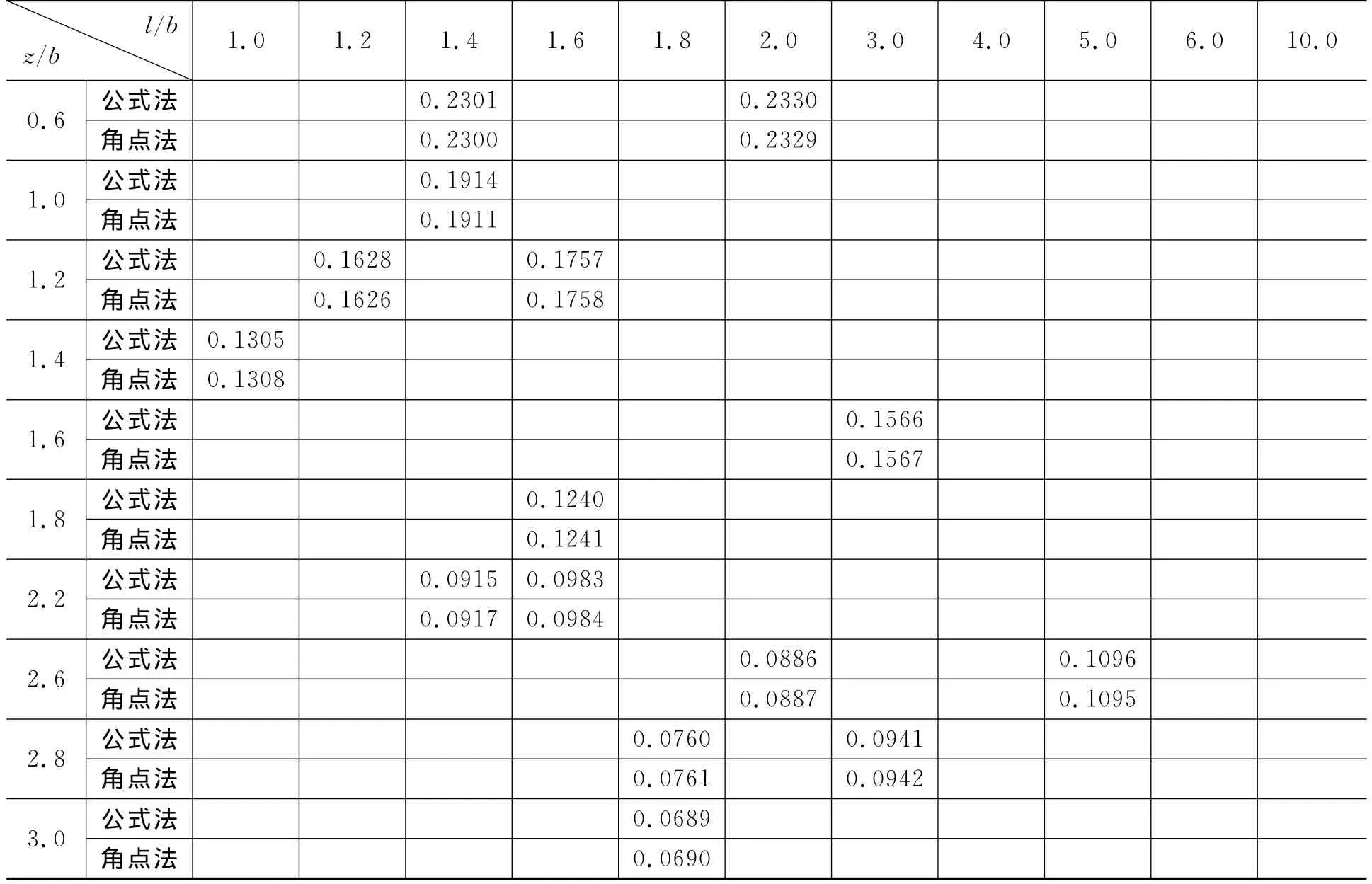
表3 公式法、角点法计算结果对照表Table 3 The comparison of the calculated results by the corner point method and the formula method

续表3

c.文中给出的对比算例中，有些结果完全一致，有些仅有很小的偏差。而偏差出现的原因可能是由于角点法计算过程中内插取值不同。

d.公式法达到了“速算”程度，只要给出矩形的长（l）、宽（b），就可计算任意点（x，y，z）的附加应力系数，极大地方便了工程技术人员在实际工作中的运用，也避免了查表内插因人而异产生的差异及角点法计算过程中因对不同矩形需进行l/b、z/b计算可能出现混乱而导致的错误。

e.需要说明的是，由公式（10）验证或推导文中所示的几种特殊的附加应力系数时，出现了分母为0的分式，这是由于在积分推导过程中这些分式分母均以代数形式给出，并一直沿袭到最后的结果。在实际计算过程中，只要将这些项不参与计算，即作为0处理即可。

f.公式法计算需要5个参数，即基础长（l）、宽（b）及计算点坐标（x，y，z）。需要注意的是坐标轴x和y的取向要与基础长、宽保持一致，不一定长边就是x轴、短边就是y轴。

g.该公式不能直接计算z＝0处的附加应力系数。若需要计算，可在Excel表中直接设置z＝0时，附加应力系数为0.25即可。

［1］陈希哲.土力学地基基础（第四版）［M］.北京：清华大学出版社，2004.Chen X Z.Soil Mechanics and Foundation（the fourth edition）［M］.Beijing：Tsinghua University Press，2004.（In Chinese）

［2］龚文惠.土力学［M］.武汉：华中科技大学出版社，2007.Gong W H.Soil Mechanics［M］.Wuhan：Huazhong University of Science and Technology Press，2007.（In Chinese）

［3］陈晋中.土力学与地基基础［M］.北京：机械工业出版社，2008.Chen J Z.Soil Mechanics and Foundation［M］.Beijing：China Machine Press，2008.（In Chinese）

［4］陈希哲.土力学地基基础（第二版）［M］.北京：清华大学出版社，1989.Chen X Z.Soil Mechanics and Foundation（the second edition）［M］.Beijing：Tsinghua University Press，1989.（In Chinese）