哈林图的零阶广义Randic指标的若干极值问题

刘顺琴

（厦门大学嘉庚学院 信息与计算科学系，福建 漳州 363105）

哈林图的零阶广义Randic指标的若干极值问题

刘顺琴

（厦门大学嘉庚学院 信息与计算科学系，福建 漳州 363105）

当α＞0（α＜0）时，确定了n阶哈林图中具有最小（最大）零阶广义Randic指标的图类；当α=-1及--时，给出了有t片树叶的树图对应的哈林图中具有最大和最小零阶广义Randic指标的图类。

哈林图；树叶；最小；零阶广义Randic指标

1 零阶广义Randic指标

著名的化学家Randic在1975年研究分子结构时引入了图的一个重要的拓扑不变量χ，其中χ定义为图G=（V，E）中所有顶点对的度数的乘积开方再求倒数之和，即

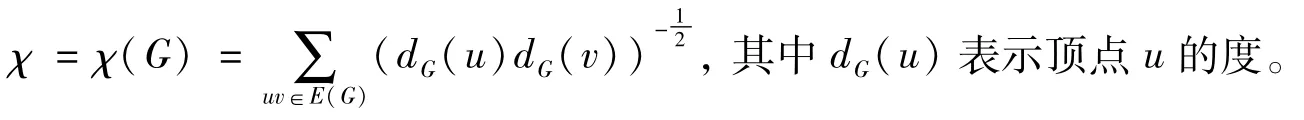
Randic同时指出该分支指标与烷烃类物质的很多物理性质和化学性质都显示出了巨大的关联性，如临界温度、生成焓、表面积以及水溶解度等等，称χ为分支指标后面，直接将该指标成为图的Randic指标。

Randic已经被多数的化学家们接受，该指标能够非常好地描述分子的结构特性和结构活性之间的关联性，甚至是一个广受化学家们喜爱的拓扑不变量，B.Bollobas联合P.Erdos在1998年将Randic指标中的推广到任意一个非零实数α，提出了广义的Randic指标，即

L.B.Kier和L.H.Hall于1977年在文献【1】当中定义了零阶Randic指标如下：

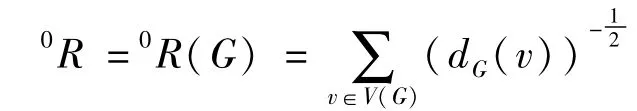
后来，X.Li和J.Zheng在文献【2】中提出了图的零阶广义Randic指标0Rα，就是将零阶Randic指标当

2 哈林图

定义：哈林图是这样得到的，对于没有2度定点的n（n≥4）阶树的平面嵌入，将其树叶按顺序连成一个圈，这样得到的平面图称之为哈林图。

例如，如下的轮图L（n）和星形图S（n）：

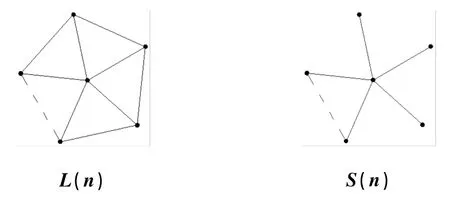
可以看出，n阶轮图L（n）是通过n阶星形图S（n）（树）得到的哈林图。

从同构的意义上看，其具有唯一性，但是这一点并不具备普遍性，例如：如下两棵树T1和T2，显然T1同构于T2，但它们所对应的哈林图H1并不同构于H2。

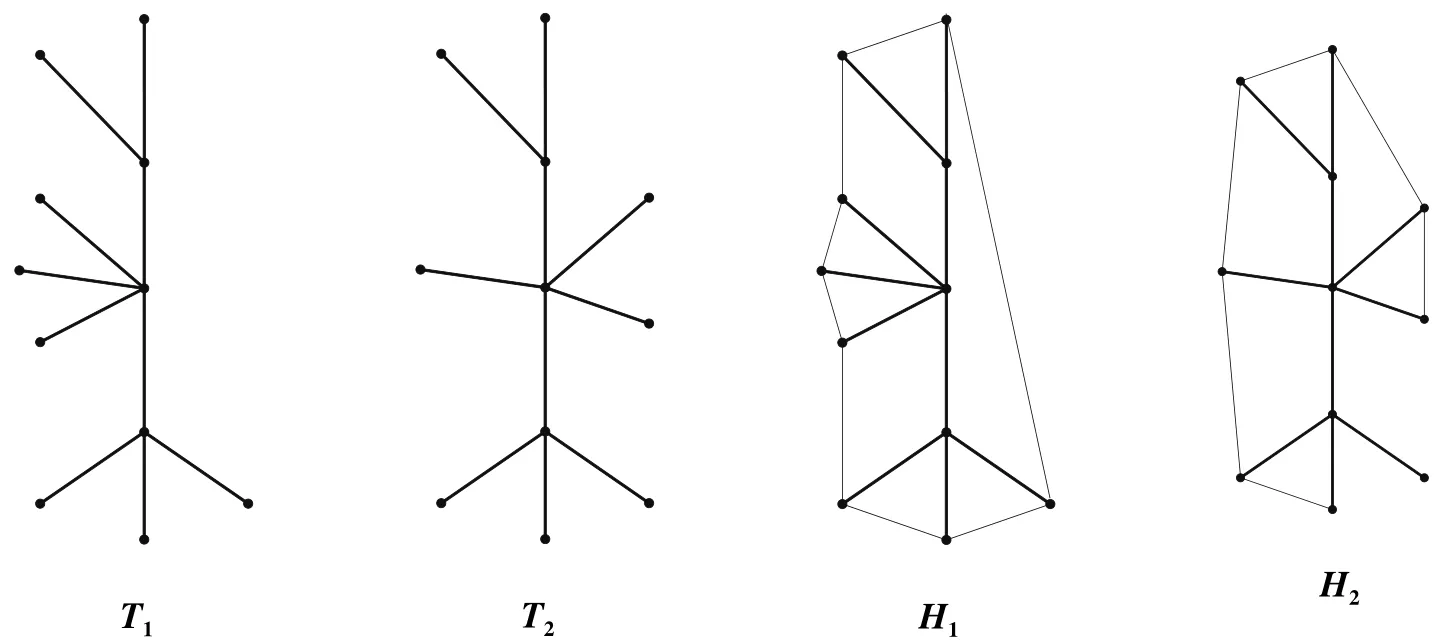
为了讨论方便，我们先定义如下几个哈林图的图类：

设λ（n）是所有哈林图的集合；

设Γ是如下n阶的哈林图的图类；

当n=2k时，Γ表示所有的三正则的哈林图的集合；

当n=2k+1时，Γ表示由一个顶点度数为4，其余顶点度数均为3的哈林图的集合。

设Γ（t）表示具有t片树叶的树图所对应的哈林图的集合，并且在该集合中定义下面两个子图类：

Γm（t）表示至少有t个顶点（对应树图当中的t片树叶）的度数为3，其余顶点度数要么为要么为但最后度数总和要等于2n+2t-2的哈林图的集合。

ΓM（t）表示由一个顶点的度数为2t+1-n，其余顶点度数为3的哈林图的集合。

3 哈林图零阶广义Randic指标的极值问题

定理1：设H是λ（n）中的一个哈林图，则有：

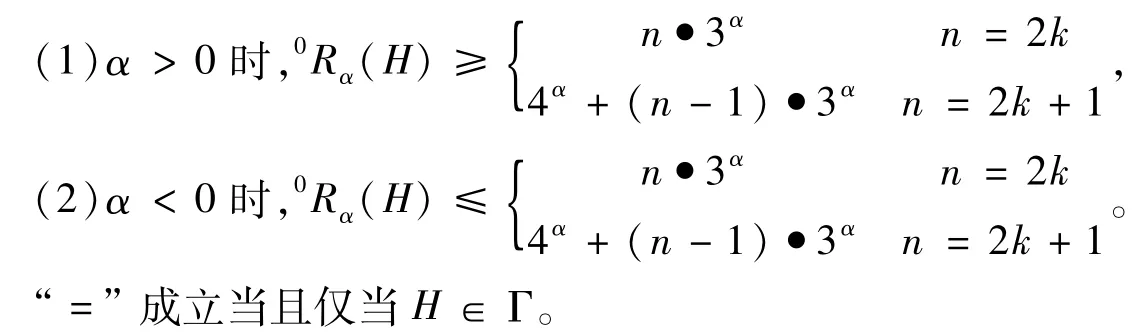
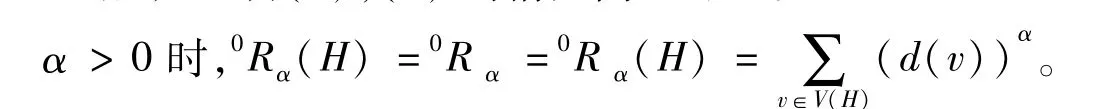
取等号当且仅当H是一个三正则图，要求n为偶数，所以n=2k时，H是一个三正则的哈林图；当n=2k +1时，不存在n阶三正则图，自然没有三正则的哈林图，至少有一个顶点的度≥4，则0Rα（H）≥4α+（n-1）·3α，取等号当且仅当有一个顶点度数为4，其余顶点度数为3，即有0Rα（H）≥由Γ的定义，可知，等号成立当且仅当H∈Γ，

我们用D（H）=（d1，d2，…dn）表示哈林图H的度序列，这里di表示第i个顶点的度，设di≥dj≥4，设哈林图H′是用顶点对（di+1，dj-1）代替图H的顶点对（di，dj）而得到的，

引理1：对于上面描述的H和H′，有

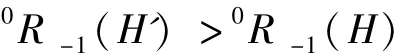
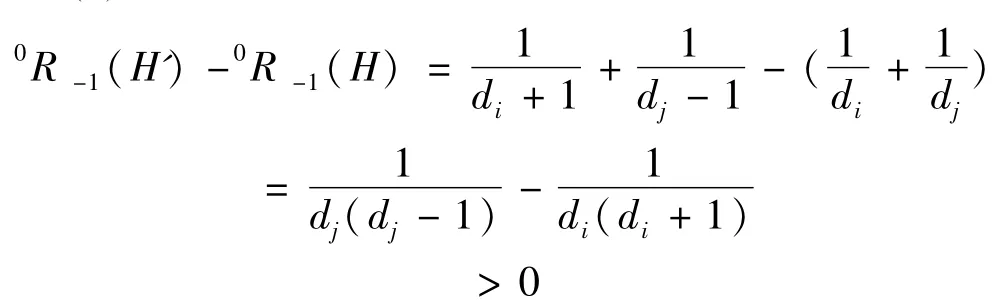
因此，引理1得证。

同样用D（H）=（d1，d2，…dn）表示哈林图H的度序列，若有di-dj≥2，哈林图H″是用顶点对（di-1， dj+1）代替H中的顶点对而得到的。

根据引理1，我们有下面的推论：

推论：对于上面描述的H和H″，有

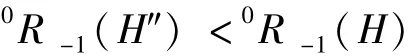
定理2：

对任意H∈Γ（t），H1∈Γm（t），H2∈ΓM（t），有

证明：由引理1，对于具有t片树叶的树图，其对应的哈林图H的边数是n-1+t且3度顶点的个数至少是t（即原来的树图中的t片树叶所对应的顶点数），为方便讨论，在H中，我们还是把这t个顶点称为‘树叶'。

对任意H∈Γ（t），若H∉ΓM（t），则有满足di≥dj≥4的顶点对按照引理1，我们对度序列进行调整，则将调整为（di+1，dj-1），调整之后的度序列所得到的哈林图H′满足0R-1（H′）＞0R-1（H），若H′的度序列（d1′，d2′，…dn′）中仍然有di′≥dj′≥4，则继续调整为（di′+1，dj′-1），……，调整到不能再调整为止，这个时候得到的哈林图H2的度序列（d1′′，d2′′，…dn′′）当中，最多只有一个顶点v的度大于3，其余顶点的度均为3（否则可以继续调整），按照握手定理，此时d（v）自然为（2n+2t-2-3（n-1））= 2t+1-n，按照ΓM（t）的定义，有H2∈ΓM（t）。

对任意H∈Γ（t），若H∉Γm（t），即除了有t个‘树叶'的度数为3之外，有其余顶点的度数满足di-dj≥2，则将调整为（di-1，dj+1），则按照引理1的推论，我们知道，得到的哈林图H″满足0R-1（H″）＜0R-1（H），若仍然有H″∉Γm（t），则继续将度序列进行调整，调整到不能再调整为止，得到的图记为H1，则H1中除了t片树叶的度数为3以外，其余顶点的度最多只差1，按照握手定理，则H1其余顶点的度数要么为⌊且总度数要等于2n+2t-2，按照Γm（t）的定义，有H1∈Γm（t）。

从证明过程可以看出，0R-1（H1）=0R-1（H）当且仅当H∈Γm（t），0R-1（H）=0R-1（H2）当且仅当H∈ΓM（t）。

定理证明完毕。

引理2：对于上面描述的H和H′，有

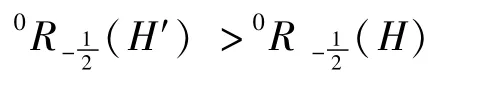
证明：

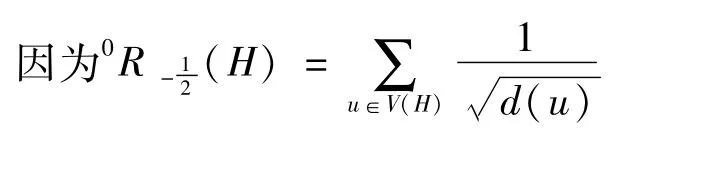
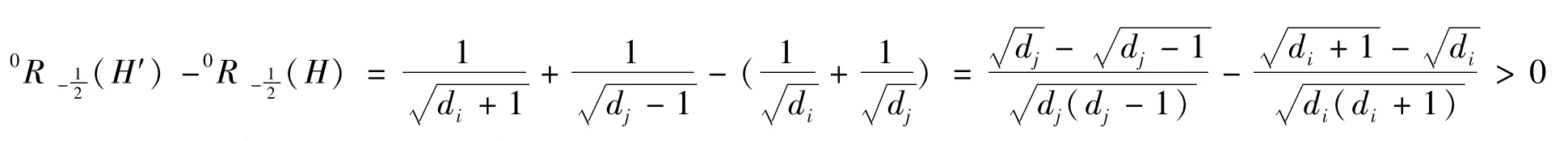
推论：对于上面描述的H和H″，有

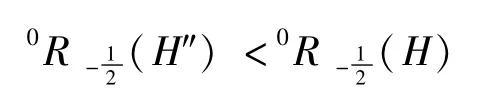
证明：道理同引理1的推论，省略。

定理3：

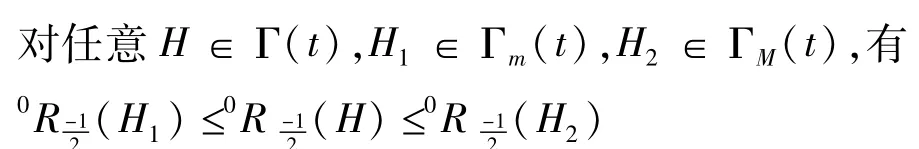
其中0

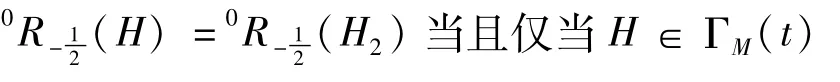
证明：根据引理2及其推论，证明过程与定理2完全相同，省略。

［1］ L B Kier，L H Hall，The nature of structure-activity relationshiPs and their relation tomolecular connectivity［J］.EuroP.J.Med.Chem，1997（12）：307-312.

［2］ X Li，JZheng，A unified aPProach to the extremal trees for different indices［J］.Math ComPut Chem，2005（6）：137-142.

［3］ 陈锦松，郭晓峰.关于Randic指数及图的直径［J］.厦门大学学报（自然科学版），2009（4）：467-469.

［4］ 林启法，钱建国.给定最大匹配数的树的零阶广义Randic指标［J］.纯粹数学与应用数学，2010（2）：153-157.

［5］ 郝晓辉，李宝凤.关于图的似拉普拉斯谱半径［J］.数学的实践和认识，2008（4）：158-160.

［6］ 叶圣奎，陈胜.图的LaPlace谱半径的几类上界［J］数学学报，2008（2）：235-240.

［7］ 冯长君，陈艳，堵锡华.改进的连接性指数用于链烷烃热力学性质与沸点研究［J］.吉林大学学报（自然科学版），2000（3）：80-84.

［8］ 张惠玲，曲安京.共轭单圈图的广义Randic指标［J］.计算机与应用化学，2013（6）：648-650.

［9］ 王波，冶成福.单圈图σ指标的次小值［J］.东北师范大学学报（自然科学版），2009（2）：18-24.

［10］ 陈娅红.完美匹配单圈图的维纳指数［J］.上海交通大学学报，2010（6）：844-848.

［11］ 朱建明，许涛，何新英.二部图上完美匹配的正交匹配分解［J］.运筹与管理，2008（4）：51-55.

［12］ 王世英，方坤夫.一些图的完美匹配多面体的维数［J］.郑州大学学报（自然科学版），2000（2）：1-3.

责任编辑：程艳艳

Some Extremum Problem s of Halin GraPhsWith Zero-order General Randic Index

LIU Shunqin
（DePartment of Information and ComPuter Science，Tan Kah Kee College of Xiamen University，Zhangzhou 363105，China）

We characterize the graPhs that have the smallest（largest）zero-order general Randic index in Halin graPhs with n-order whenα＞0（α＜0）；Also，we give the Halin graPhswith the smallest（largest）zero-order general Randic index corresPonding to the tree graPh with t Pieces of leaves whenα=-1 or-

Halin graPhs；tree graPh；the smallest；zero-order general Randic index

O157.5

A

1009-3907（2015）06-0053-04

2015-03-16

福建省科技厅自然科学基金项目（JB13269）

刘顺琴（1981-），女，福建泉州人，讲师，硕士，主要从事应用数学方面研究。