基于广义费用函数的高铁票价双层规划模型研究

韦凌翔，陈红，蒋金亮，王韩麒，邵海鹏

(1.长安大学 公路学院，陕西西安710064;2.武汉市交通科学研究所，湖北武汉430015)

根据国务院2004年提出的《中长期铁路网规划》，到2020年，我国将建成1.2万 km的高速铁路，届时将形成“四纵四横”的铁路快速客运通道以及环渤海地区、长江三角洲地区、珠江三角洲地区的3个城际快速客运系统，覆盖区域内主要城镇。客运通道内高速铁路的大规模建设，不仅可以缓解我国长期存在的铁路运能与运量之间的矛盾，大规模提升铁路技术装备水平，同时可以满足人民群众日益增长的多元化出行需求［1］。而高速铁路的运营效果往往直接通过票价收入体现出来。高速铁路的票价过高，超过旅客的平均承受能力，就会造成高铁旅客运量向别的交通方式上转移，从而造成高铁旅客运量不足，难以取得理想的客运收入和社会效益;高速铁路票价过低，铁路部门不仅难以取得合理的经济效益，甚至无力偿还高铁建设投资，造成巨大的债务负担，而且过低的高铁票价会将大量客运量转移到高铁上来，可能引起高铁能力紧缺。因此制定合理的高铁票价对均衡各种运输方式的比例、满足旅客出行需求、保证高铁运营单位正常运作、提升高铁整体服务水平等方面具有重要意义［2－3］。在高速铁路建设如火如荼的背景下，高铁旅客票价的制定及优化问题也受到了国内外专家学者的关注。魏安清［4］应用经济学中的有效性原理，来对运输票价制定的相关问题进行分析，并运用运输票价制定的效率准则，制定出未来年成渝通道中高速铁路的最优票价;卞长志等［5］建立各交通方式的运营利润模型，并以运营票价为竞争策略变量，建立城际铁路和公路长途巴士运输的完全信息静态博弈模型;四兵锋等［6］利用灵敏度方法分析了票价与不同运输方式的客流量的影响关系;Gerard等［7］根据改进的经济需求模型对英国的铁路票价进行经济评价，并从一些票价集合中选出最优票价。然而有关高铁票价优化的研究不深，目前我国仍然没有一套完整的理论和计算方法来计算高速铁路旅客票价。京津城际、沪杭城际铁路运营后，线路上采用的均为试运价模式。此外，我国既有线旅客票价制定方法一般是以定性分析为主或定性分析与统计数据分析相结合的刚性定价法，采用这种方法制定高速铁路客票价格，运输企业对市场变化反应迟缓，无法针对旅客需求实施及时有效的调整，在市场竞争中处于被动地位，并将逐渐失去竞争力。因此，正确把握客运量与票价之间的调整关系，对高速铁路票价进行合理的优化，以使其发挥最大的社会、经济效益是迫切需要解决的难题。基于以上分析，本文拟从出行者选择出行工具影响因素出发，建立考虑安全性、快捷性、经济性、舒适度、方便性等五大服务特征因素的广义费用函数;从而构建考虑旅客和高铁运营单位这2个矛盾体双重利益的双层规划模型，其上层规划描述高铁运营单位在政府规定的范围内制定最佳票价策略以实现企业自身的目标，下层规划则描述旅客在城际间各种运输方式竞争合作条件下广义出行费用最小的目标;进而采用内罚函数算法拟设计基于径路流量的Frank－Wolfe算法的求解步骤;最后，以京沪高路实例验证所提出的模型与算法的合理性。

1 广义费用函数构建

广义出行费用函数描述了旅客在出行过程中付出的代价，它的广义定义为对出行有影响的各种因素的综合效用。从出行者的角度分析，不同运输方式客流分配结果取决于出行者对运输方式进行选择的结果［8］。在运输通道内供旅客选择的出行方式不是单一的，旅客可根据各种运输方式的服务特性并结合自身的经济条件和出行目的进行选择。根据效用理论，出行者在特定条件下，会选择其认为效用值最小的交通方式出行［9］。因此，本文构建考虑不同服务特征的高铁的运输通道广义费用函数。

1.1 不同服务特征的广义费用函数分析

目前，国内外有关分担率模型的研究大多考虑安全性、快捷性、经济性、舒适度、方便性等五大服务特征因素［10］。基于对上述五大服务特征因素的考虑制定了适合本文的广义费用函数，并通过对基础数据来进行参数的拟合，从而建立对应的广义费用函数。

1.1.1 安全性(Si1)

旅客选择运输方式时，首先考虑的是安全性。安全性主要根据安全可信度来衡量。当伤亡事故率为0时，安全可信度为l;当伤亡事故率超过一定限度，安全可信度为0，视为不安全。具体计算公式如下:

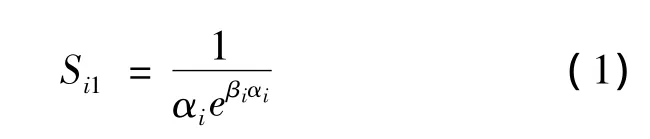
式中:αi是第i中运输方式的伤亡事故率，αi和βi为待定系数。

1.1.2 经济性(Si2)

旅客接受运输服务的前提是支付相应的运费，因此票价的高低是影响旅客运输方式选择的重要因素。正常情况下，运费应包括旅行过程中门到门的所有费用，但是由于各方案与主要交通工具衔接所需费用在总费用中的比重很小，故宜以旅客在主要交通工具上所支付的票价来衡量经济性这个指标。各种运输方式的票价等于运价率与旅行距离的乘积。具体计算公式如下:式中:Ri为第i种运输方式的运价率;Li为第i种运输方式的旅行距离;λi为第i种运输方式可能出现的折扣率。

1.1.3 快速性(Si3)

交通运输的运行时间包括运输工具的运行时间和衔接时间，因此可以用这2项时间之和作为快速性的衡量指标。具体计算公式如下:

式中:V(T)AB指从A到B的旅客时间价值;vi为第i种运输方式的旅行速度;li为居民从居住小区到车站的市内交通距离;v’为市内交通距离。

旅客时间价值采用生产法进行计算。生产法时间价值的一般定义为:旅客在旅行中消耗的时间，若用于从事生产活动所能创造的价值［11］。其计算公式如下:

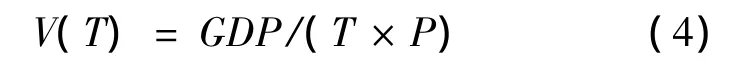
式中:GDP指地区国民生产总值;T为平均劳动时间;P为区域人口。

1.1.4 方便性(Si4)

运输方式的方便性也是旅客交通方式选择行为的重要影响因素，方便性越好，旅客越倾向于该运输方式。以上下车时间、候车时间作为方便性的衡量指标。其计算公式如下:

1.1.5 舒适性(Si5)

舒适性是现代旅客运输追求的重要服务特性之一。舒适性以旅客恢复疲劳所需时间来标度。恢复疲劳所需时间越长，其舒适性越差，反之则舒适性好。旅客在旅途中的疲劳程度与其旅行时间是成正比关系的。对于健康的旅客，无论乘坐何种交通工具，旅行多长时间，从人的生理角度来看，基本恢复疲劳的时间不会无限增长。在此，本文给定一个恢复疲劳的极限时间H。可以认为，恢复疲劳所需时间与旅行时间t和乘车环境相关，用恢复疲劳所需时间计算公式以及疲劳恢复时间的价值转化值(Si5)表示为:

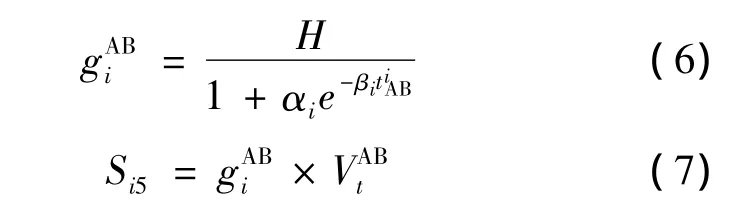
1.2 广义费用函数定义

在以上构建的五大不同服务特征的广义费用函数中，安全性因素相对其他4个因素而言具有独立性，且安全性因素无法进行价值转化。因此，将其他4个因素放在一起进行权重组合然后再与安全性因素相乘，以此来定义第i中运输方式的广义费用权重值Vi，具体形式如下:

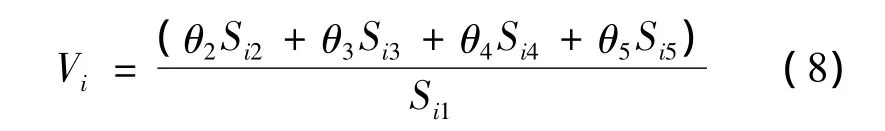
式中:θ2，θ3，θ4和 θ5分别为对应因素的服务特性权重;式中其他符号含义同上。

服务特性权重参数θi的确定对客流分配计算结果起决定性的作用，其值的确定需要在大量调查数据的基础上采用数学方法进行标定。孙朝苑［13］对服务特性参数进行了一定程度的研究，因此借用文献［13］的研究结论确定服务参数值。

根据文献［13－14］，广义费用函数f常用的形式有幂函数和对数函数形式，在本研究中采用前者，具体形式如下:

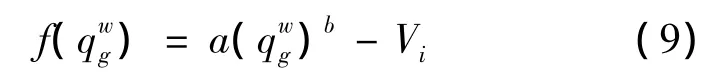
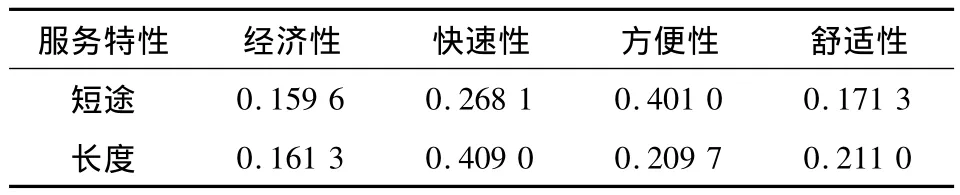
表1 服务参数值表Table 1 Parameter value table of service

式中，a，b为待定参数，可通过交通调查和统计分析的方法获得。

2 双层规划模型与求解算法设计

2.1 模型介绍

高速铁路票价的制定问题可以看作是一个Leader－Follower问题，其中决策部门即高铁客运企业是指导者(Leader)，旅客的出行行为为跟随者(Follower)。铁路运输部门可以通过票价和服务质量等方面的改变来改变铁路客运的广义出行费用，从而影响旅客在出行时对出行方式的选择，而不能控制其的选择行为［15］。旅客通过对现有的出行方式进行对比分析，从而根据自己的需求来选择合适的出行方式。这种关系和双层规划模型的定义基本一致，上层规划描述高铁运营企业在政府规定的范围内制定最佳票价策略以实现企业自身的目标，下层规划则描述了城际间各种运输方式竞争合作条件下，客流在不同运输方式间的分担率模型，其分配原则即为使旅客出行者广义出行费用最小。双层规划的一般形式如下:

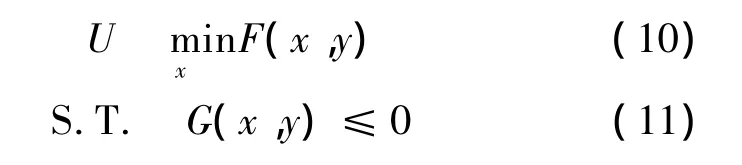
其中y=y(x)由下述规划求得:

双层规划模型是由上层模型U和下层模型L组成。上层决策者通过设置x的值影响下层决策者，从而限制了下层决策者的可行约束集，上层决策者通过下层决策者的目标函数与下层决策者相互作用。同时，值得注意的是，下层决策变量y是上层决策变量的函数，即y=y(x)，这个函数即为反映函数［15－16］。上层规划的目标函数为客运企业或交通管理部门的期望目标，比如客运企业的经济效益最大化或者社会效益最大化等。在本文中上层规划的决策变量是高铁票价，下层规划的决策变量为不同客运方式的客流量，反映函数则表示高铁客流量与高铁票价的关系。

2.2 模型建立

2.2.1 上层规划

从高铁运营单位的角度来看，其目的在于市场盈利最大化，也就是高铁客票收入减去高铁客运可变成本的值的最大值，即上层规划的目标函数。同时，政府部门对高铁票价具有一定的指导作用，在国家旅客运输政策没有较大变动的情况下，高铁票必须限定在上限和下限之间，其中上限为政府规定的最高限价，下限为高铁人均客运成本。综合考虑后，建立上层规划模型如下:

2.2.2 下层规划

下层规划是一个交通流分配模型，采用Beckmann交通平衡分配模型进行流量分配。在不考虑换乘的前提下，OD对之间的不同出行方式的出行路径是相对确定的，都是沿着固定的线路运行，因此，可以将这些交通方式之间的流量分配等效成路段流量分配模型来进行交通方式间划分。

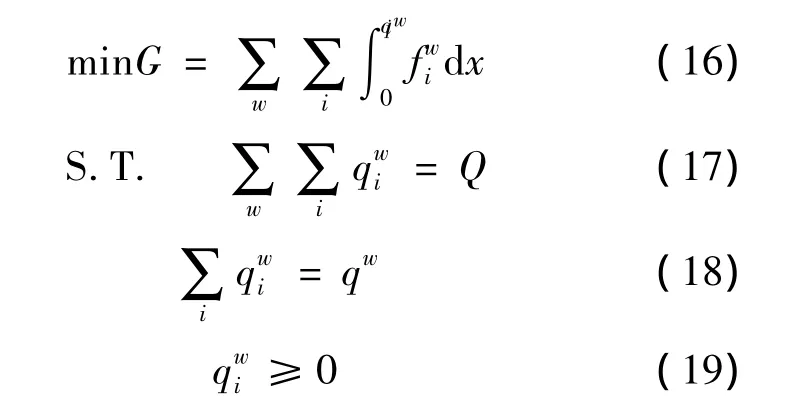
式中:式(16)为目标函数，表示旅客出行者广义费用值最小;式(17)和(18)为总流量平衡和单一OD对流量平衡约束;式(19)为非负性约束。w表示OD对;表示第w个OD对间第i种交通方式上的客流量;表示第w个OD对间第i种交通方式的费用函数;Q表示目标区域总客流量;qw表示第w个OD对之间的客流量。

2.3 求解算法设计

求解双层规划问题的关键在于找到反映函数y(x)的具体形式，即客流量与票价的函数关系。为此本文首先从下层规划模型入手，采用Frank－Wolfe算法得到高铁客流量的函数表达式，带到上层规划模型中，利用数学优化软件Lingo进行求解，然后将Lingo得到的最优解带到下层规划中，得到高铁客流量新的函数表达式，依次类推，直至最后Lingo得到的最优解收敛于某一个值为止，此时算法结束。从上文的分析容易看出，该模型的求解难点在于下层规划的求解过程。因此，论文对下层规划的Beckmann交通平衡分配模型进行算法介绍。求解网络均衡配流模型最常用的算法是基于径路流量的Frank－Wolfe算法，但是由于上文中下层规划模型中增加了能力约束，模型就不能直接应用该算法来求解。因此，论文采用内罚函数算法对下层规划模型进行求解。所谓内罚函数就是通过罚函数将能力约束转换为目标函数的一个惩罚项，将其转换为一个没有能力约束条件的配流模型，然后用Frank－Wolfe算法对模型进行求解。

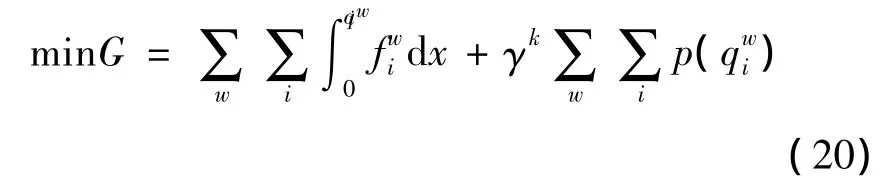
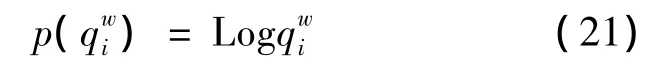
目标函数等价于如下等式

求解下层规划算法的具体步骤如下:

Step1:初始化。设置初始化惩罚参数γ，并且设置循环次数j=0;

Step2:用Frank－Wolfe算法求解在惩罚参数γ条件下的模型，具体步骤如下:

4)确定迭代步长:用二分法求满足下式的λ:

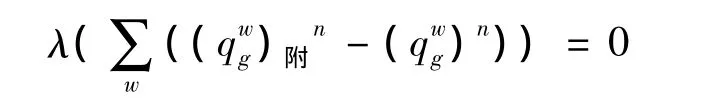
6)收敛性检验:如果满足

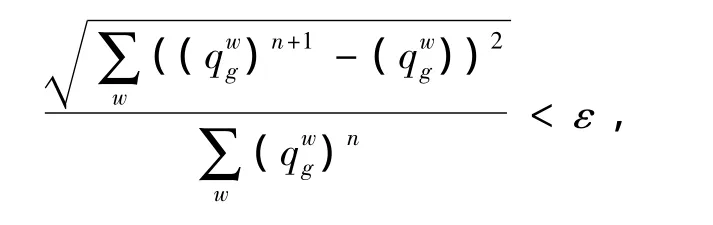
Step3:更新惩罚参数γ=δγ(δ为γ的衰减因子，为0～1之间的数)，j=j+1;

Step4:收敛判断。如果惩罚参数趋于0，则算法停止，否则，转到第2步。

双层规划算法具体操作步骤如下:

第1步:设高铁票价率的初始值为ci;

第2步:将ci带入下层规划模型中，求出对应高铁客流量qi;

第3步:利用灵敏度分析方法求得反应函数的近似形式qi(ci);

第4步:将反应函数带入上层规划目标函数中求得新票价率{c(i+1)};

第5步:收敛判断，如果|c(i+1)－ c(i)|＜=δ，算法结束;否则令 c(i)=c(i+1)，转到第2步。

3 实例验证

京沪高铁于2011—06通车，从北京南站出发终止于上海虹桥站，总长度1 318 km。京沪高铁建成通车后呈现出普通铁路、航空、公路以及高铁为客源而相互竞争的局面，因此制定合理的高铁票价以增强高铁的竞争优势至关重要。本文以京沪高铁实例验证该模型的有效性。

根据基础数据及1.1节中的分析计算出各运输方式的服务因素值。其中高铁速度取300 km/h，高速公路的长途巴士取100 km/h，普通铁路客运列车取120 km/h，航空根据飞行时间为准，两城市的平均时间价值取45.71元/h。服务特征参数的具体取值如表2所示。

按照1.2节中表1的取值，计算得到旅客单次单程出行中各运输方式的广义费用函数值如图1所示，图中符号下标数字1表示高铁、2表示航空、3表示高速公路、4表示既有铁路，λi为各种运输方式可能出现的折扣，普通铁路不考虑打折情况。其中，λ1=0.8，λ2=0.6，λ3=0.9。

由图1可知，本文选用的网络中只存在1个OD对(北京—上海)，高铁运营成本取z1=0.32元/人km，票价率的上限和下限分别为cmax=1.50元 /人km，cmin=0.10元 /人km。每日客运总量为23.2万人次(2013年统计数据)。借助Lingo软件，按照本文设计的模型求解算法，求解出高铁最优票价为c=0.65元 /人km，票价为:c*1 318=857元。将本模型计算的票价结果与2014年9月中国铁路服务中心公布的上海至北京的高铁票价对比(如图2)。由图2可知，该模型计算出的位于一等座与二等座票价之间，但是略低于中国铁路服务中心公布的平均票价。因此，可以得出以下结论:该模型计算的票价具有现实可借鉴性，可为高铁票价的制定提供较为科学的依据。

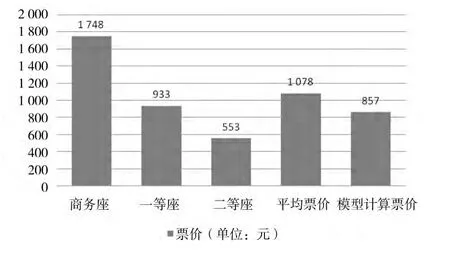
图2 高铁票价对比图Fig.2 Comparison chart of high － speed rail fare

4 结论

1)从出行者选择出行工具影响因素出发，基于对安全性、快捷性、经济性、舒适度、方便性等五大服务特征因素的考虑制定了适合本文的广义费用函数，并通过对基础数据来进行参数的拟合，从而建立能较好表征不同服务特征的广义费用函数。

2)构建了关于制定高铁票价双层规划模型，通过找到合理的票价策略从而达到决策部门的目标，即考虑到保证乘客自身所选择的出行方式的广义出行费用最小化与铁路客运企业达到客运经济效益最大化的目标。

3)设计了采用内罚函数算法对下层规划模型进行求解的思路，即通过罚函数将能力约束转换为目标函数的一个惩罚项，将其转换为一个没有能力约束条件的配流模型，然后用Frank－Wolfe算法对模型进行求解。

4)以京沪高铁实例验证所提出的模型与算法的合理性，通过该模型制定的高铁票价具有现实可借鉴性，可为高铁票价的制定提供较为科学的依据。京沪高铁共有24个高铁站，总共产生276个OD对，本文仅以北京—上海之间的单一OD对为代表进行了验证，基于多个OD对的实例验证有待深入研究。

［1］王凤学.中国高速铁路对区域经济发展影响研究［D］.长春:吉林大学，2012.

WANG Fengxue.Study on the influence of China highspeed railway on regional economic development［D］.Changchun:Jilin University，2012.

［2］Vickrey W S.A proposal for revising New York＇s subway fare structure［J］.Journal of the Operations Research Society of America，1955，3(1):38－68.

［3］曹灿明，陈建军.高速铁路客运服务质量，旅客满意度与忠诚度分析［J］.铁道学报，2012，34(1):1－6.

CAO Canming，CHEN Jianjun.Analysis on service quali-ty，passenger satisfaction and passenger loyalty relationship of high － speed railways［J］.Journal of the China Railway Society，2012，34(1):1－6.

［4］魏安清.运输通道客运专线最优票价制定研究［J］.黑龙江交通科技，2008，30(12):179 －180.

WEI Anqing.Transportation corridor passenger line optimal fare formulate research［J］.Communications Science and Technology Heilongjiang，2008，30(12):179 －180.

［5］卞长志，陆化普，尉欣欣.城际铁路和公路长途客运的定价博弈［J］.交通运输系统工程与信息，2009，10(1):184－189.

BIAN Changzhi，LU Huapu，YU Xinxin.Price game between intercity railway and bus［J］.Transportation Systems Engineering and Information，2009，10(1):184－189.

［6］四兵锋，高自友.铁路旅客票价与客流量之间的灵敏度分析［J］.铁道学报，1999，21(4):13－16.

SI Bingfeng，GAO Ziyou.Sensitivity analysis for the relationship between railway passenger fare and passenger flow volume［J］.Journal of the China Railway Society，1999，21(4):13－16.

［7］Gerard Whelan，Richard Batley，Jeremy Shires，et al.Optimal fares regulation for Britain’s railways［J］.Transportation Research，2008，44:807－819.

［8］陈绍宽，刘爽，何宇强，等.城市间旅客运输需求预测模型研究［J］.交通运输工程与信息学报，2009，7(1):38－43.

CHEN Shaokuan，LIU Shuang，HE Yuqiang，et al.Passenger transport demand prediction between cities［J］.Transportation SystemsEngineering and Information，2009，7(1):38 －43.

［9］杨文国，高自友.考虑环境因素的广义用户平衡和广义系统最优配流模型［J］.中国公路学报，2003，16(4):72－76.

YANG Wenguo，GAO Ziyou.Generalized user equilibrium assignment model and generalized system optimization assignment model under environment［J］.China Journal of Highway and Transport，2003，16(4):72 －76.

［10］Fishburn P C.Utility theory for decision making［R］.Research Analysis Corp Mcleanva，1970.

［11］He Y，Mao B，Chen T，et al.The mode share model of the high－speed passenger railway line and its application［J］.Journal of the China Railway Society，2006(3):003.

［12］Wee H M，Law S T.Replenishment and pricing policy for deteriorating items taking into account the time－value of money［J］.International Journal of Production E-conomics，2001，71(1):213 －220.

［13］孙朝苑.客运专线对沿线城市铁路客运量分流问题的研究［J］.铁道经济研究，2004(3):44－46.

SUN Chaoyuan.Research on passenger dedicated line of shunt problems of railway passenger traffic along the city［J］.Railway Economics Research，2004(3):44－46.

［14］Keviczky L，Kumar K S P.Multivariable self－ tuning regulator with generalized cost function［J］.International Journal of Control，1981，33(5):913 －921.

［15］四兵锋，高自友.市场竞争条件下的客运价格优化策略模型及算法［J］.交通运输系统工程与信息，2007，7(1):73－78.

SI Bingfeng，GAO Ziyou.Optimal model for passenger transport pricing in market competition［J］.Transportation Systems Engineering and Information，2007，7(1):73－78.

［16］何宇强，毛保华，陈团生，等.高速客运专线客流分担率模型及其应用研究［J］.铁道学报，2006，28(3):18－21.

HE Yuqiang，MAO Baohua，CHEN Tuansheng，et al.The mode share model of the high－speed passenger railway line and its application［J］.Journal of the China Railway Society，2006，28(3):18 －21.