孔隙水作用下的二级边坡挡土墙被动土压力上限研究

张亮，罗杰

(湖南省交通科学研究院，湖南长沙410015)

边坡工程广泛存在于各类公路及铁路工程中，其稳定性和支护方法的研究一直是岩土工程工作者的研究重点［1－3］。在孔隙水作用下，边坡的稳定性较差，往往需要借助挡土墙对边坡工程进行加固。除孔隙水等外因外，边坡稳定性还与土体的内摩擦角和黏聚力等因素有关［4－5］。目前为止，岩土工程界对边坡稳定性的研究已经有了较多成果，但是对考虑孔隙水压力及地震力作用下的挡土墙土压力方面的研究仍然较少。为研究孔隙水压力及地震力等不利因素对边坡挡土墙被动土压力和边坡稳定的影响，本文建立考虑挡土墙作用的二级边坡的对数螺旋线破坏模式，基于极限分析方法上限定理，充分考虑土体重度、竖向和横向地震力以及孔隙水压力等外力和边坡破坏面上和挡土墙与墙后土体黏结力等产生的内能耗散［6－9］，采用 Bishop［10］提出的孔隙水压力计算方法对挡土墙的被动土压力和被动土压力系数的上限解进行计算分析，并运用数值计算软件对各参数对被动土压力系数的影响进行分析［11－13］。

1 极限分析上限法

极限分析方法是目前岩土工程界采用较为广泛的隧道和边坡等岩土工程的稳定性分析方法，本文应用极限分析方法上限定理对二级边坡的挡土墙被动土压力及其系数的上限解进行求解，下面简要介绍极限分析方法上限定理［14－15］。

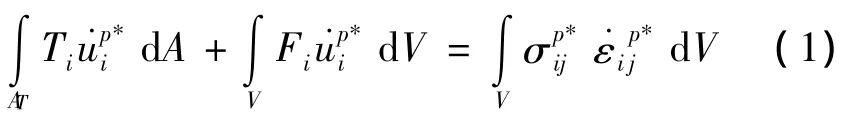
根据上限定理的基本思想，采用上限定理求解的荷载和承载力比实际情况下的荷载和承载力要大，这是由于上限定理假定岩土体处在极限状态时位移和速度已经在破坏面上发生，但是，如果位移和速度已经产生，则以为该岩土体已经发生破坏。

上限定理的正确性通过反证法不难证明，假设上限定理求得的极限荷载和承载力小于实际破坏时的荷载和承载力，此时必存在一个静力平衡的应力场，使破坏体内的所有点的屈服函数满足，将其代入到虚功方程:

将式(2)与式(1)相减得:

2 破坏机制

考虑挡土墙和锚杆支护作用的二级边坡破坏模式如图1所示，整个破坏面以点O为中心发生角速度为Ω的转动破坏，破坏面通过边坡坡趾B，边坡第1阶坡脚为β1，第2阶坡脚为β2，AB面为边坡的破坏面即速度间断面，其上任意点的线速度与该点切线之间的夹角为边坡土体的内摩擦角φ，边坡其他各要素尺寸如图1所示。

在图1所示的破坏模式中包含的外力分别为:土体重力，横向和竖向地震荷载，孔隙水压力;内力分别为:挡土墙平衡土压力的抗力和滑动面上的黏聚力。鉴于此，根据极限分析上限定理，本文需要计算的外力功率有:土体重力功率，横向地震荷载功率、竖向地震荷载功率以及孔隙水压力功率;需要计算的内能耗散功率有:速度间断面上的内能耗散功率，挡土墙被动土压力功率和挡土墙和墙后土体之间的黏结力所做的功率。

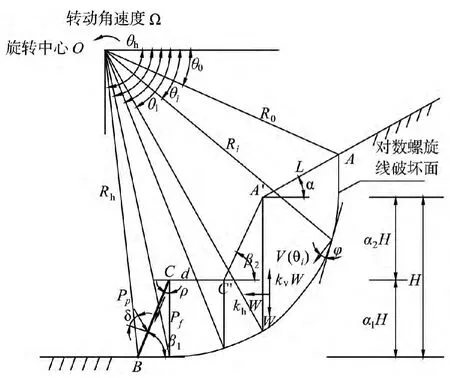
图1 考虑挡土墙和锚杆作用的边坡破坏机制Fig.1 Failure mechanism for reinforced slope

3 计算过程

本文建立的对数螺旋线形式的边坡破坏面表达式如下:

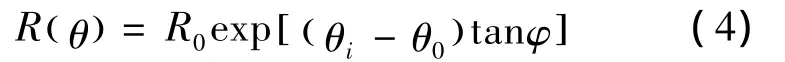
根据图1中几何关系，可知:

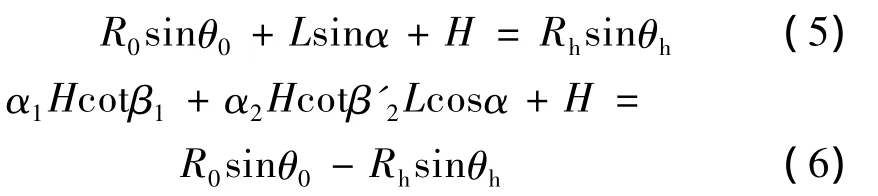
由式(2)～(3)可得:

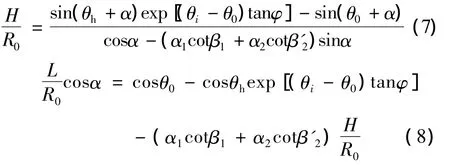
3.1 外部土体自重做功功率

3.1.1 土体重力和地震力荷载功率

边坡土体重力功率时采用叠加法进行计算，即分别计算出 OAB，OAA’，OA’C’，OCC’和 OCB 的重力功率，然后进行叠加计算出边坡ABCC’A’A的重力功率，具体过程如下。

1)曲边三角形OAB的外力功率

OAB的土重做功为:

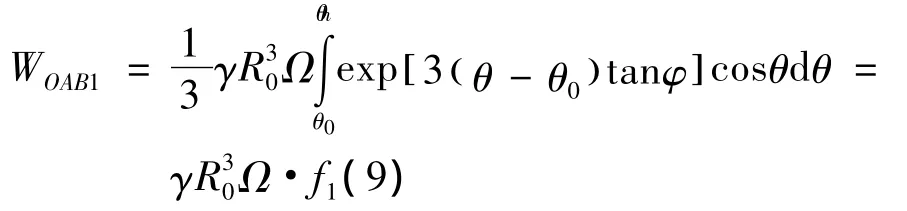
则其竖向和横向地震力荷载功率分别为:

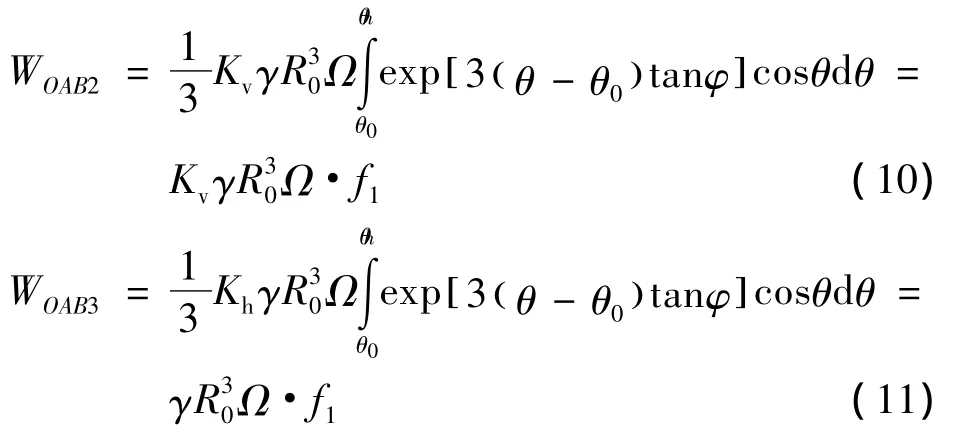
由上，曲边三角形OAB的外力功率为:

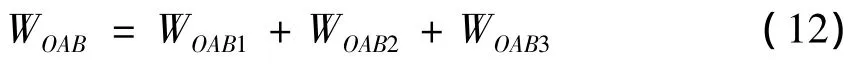
2)三角形OAA’的外力功率

三角形 OAA’的土体重度为 SOAA′=，且三角形OAA’的重心距离旋转中心的距离为，三角形OAA’的重力功率表达式为:

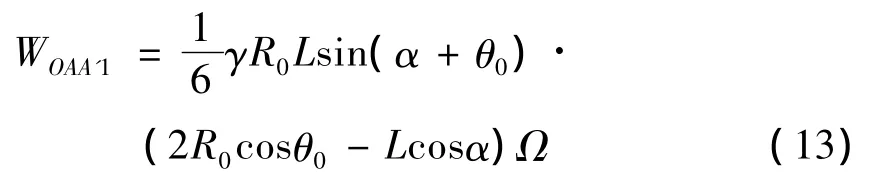
则其竖向和横向地震力荷载功率为:

由上，曲边三角形OAA’的外力功率为:

3)三角形OA’C’的外力功率

三角形OA’C’的面积表达式为:

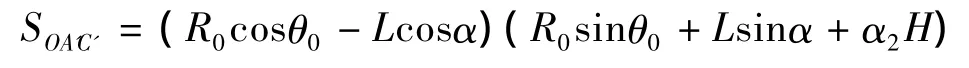
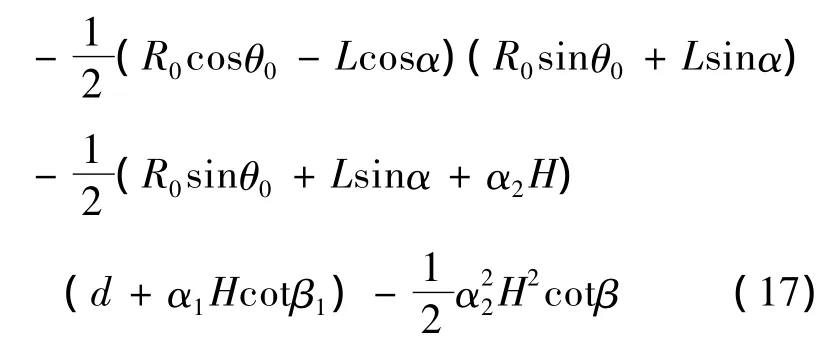
三角形OA’C’的3个顶点O，A’和C’距离破坏机构旋转中心O的铅垂线水平距离的平均值为，则三角形OA’C’的重力和竖向地震力荷载作用下的外功率为:

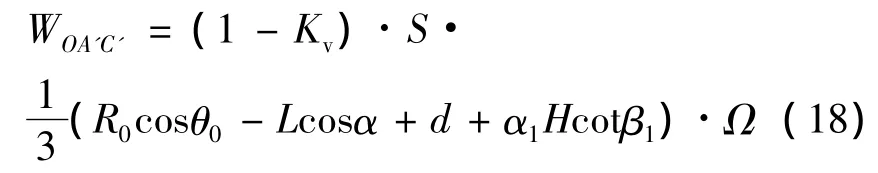
同样地，三角形OA’C’的3个顶点O，A’和C’距离破坏机构旋转中心O水平线的垂直距离的平均值为，则其横向地震力荷载的外力功率为:

由上，曲边三角形OA’C’的外力功率为:

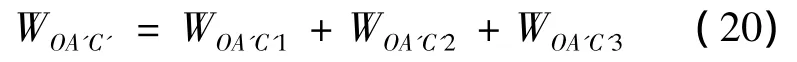
4)三角形OCC’的外力功率

三角形OCC’的面积表达式为:

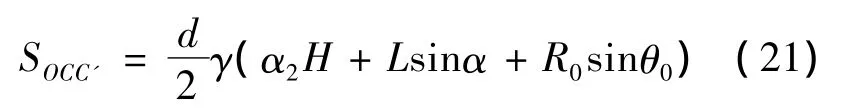
三角形OCC’的3个顶点O，C和C’距离破坏机构旋转中心O的铅垂线水平距离的平均值为，则三角形OCC’的重力和竖向地震力荷载作用下的外功率为:

同样地，三角形OCC’的3个顶点O，C和C’距离破坏机构旋转中心O的水平线的垂直距离的平均值为R0sinθ0+Lsinα +α2H，则三角形OCC’的横向地震力荷载的外功率为:

由上，曲边三角形OCC’的外力功率为:

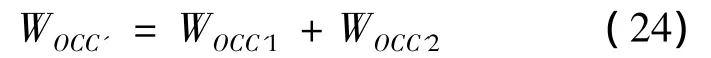
5)三角形OCB的外力功率

三角形OCB的面积表达式为:

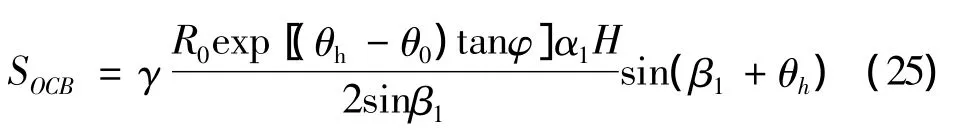
三角形OCB的3个顶点O，C和B距离破坏机构旋转中心O的铅垂线的水平距离的平均值为，则三角形OCB在重力和竖向地震力荷载作用下的外力功率为:

同样地，三角形OCB的3个顶点O，C和C’距离破坏机构旋转中心O的水平线的垂直距离的平均值为，则三角形OCB的横向地震力荷载的外功率为:

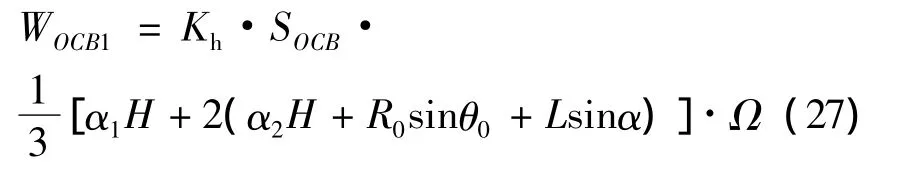
由上，曲边三角形OCC’的外力功率为:

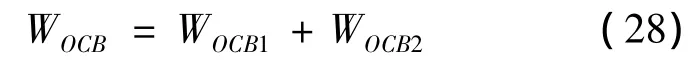
则二级边坡在重力和地震力荷载作用下产生的功率为:

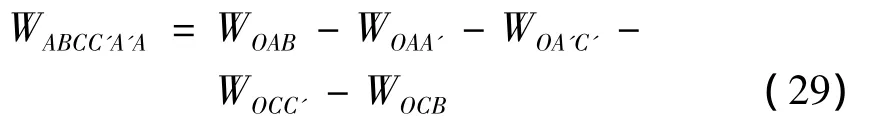
3.1.2 孔隙水压力功率

计算中采用孔隙水压力系数ru的方法将孔隙水的影响引入到边坡稳定性分析中，即孔隙水所做的外功率表达式为:

其中

z1，z2，z3和 z4的表达式如下:

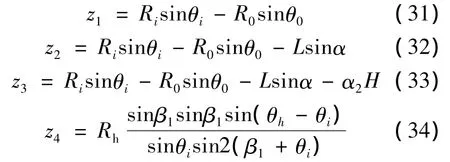
θ1，θ2和 θ3可由下式确定:

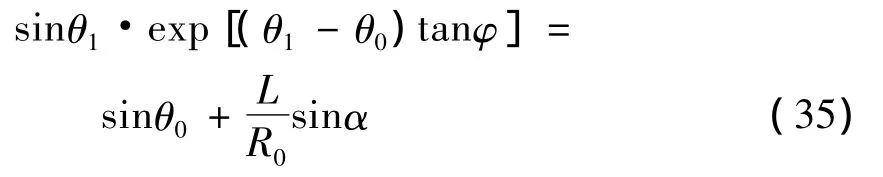
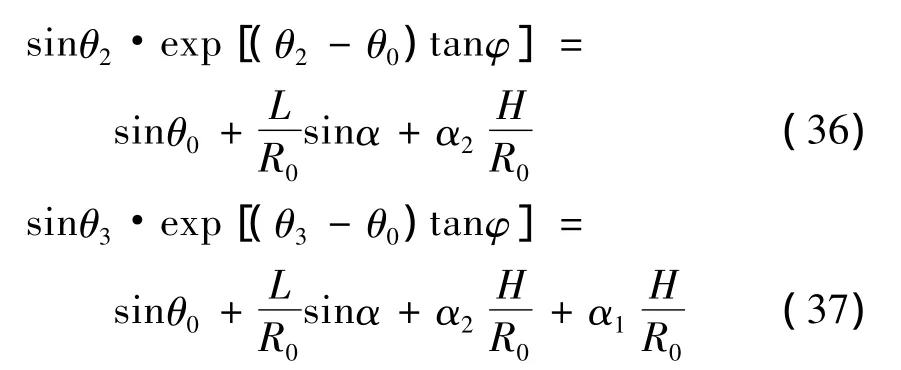
由上可以得出二级边坡的外力功率表达式:

3.2 内能耗散功率

内能耗散功率包括速度间断面AB上的耗散功率、挡土墙和墙后土体之间的黏结力的耗散功率和挡土墙被动土压力耗散功率。

3.2.1 速度间断面上的内能耗散功率

边坡速度间断面上的内能耗散功率为:

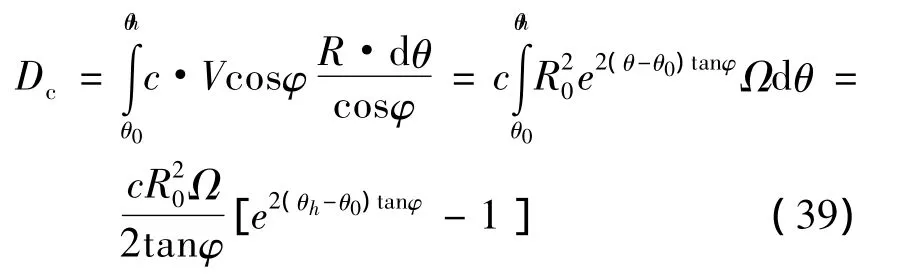
3.2.2 被动土压力功率

一般假定被动土压力合力作用于挡土墙1/3墙体高度处，如图1所示。该点距离过转动中心O点的垂线的水平距离为，距离过O点的水平线的垂直距离为，为便于计算，将被动土压力Pp分解为水平向分力Ppx=Pasin(β1+ δ)和竖直向分力 Ppy=－ Pacos(β1+δ)，则被动土压力所做功率为:

3.2.3 挡土墙与墙后土体黏附力功率被动土压力功率

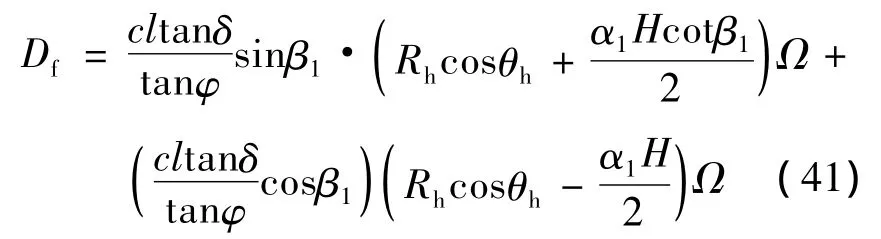
由上各式可得考虑挡土墙被动土压力作用的二级边坡内能耗散功率的表达式为:

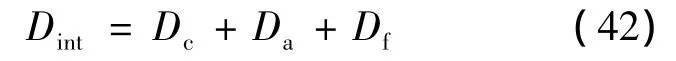
3.3 挡土墙被动土压力上限解

根据极限分析方法上限定理，令二级边坡的外力功率与内能耗散功率相等即Wout=Dint可得出被动土压力的上限解，即:

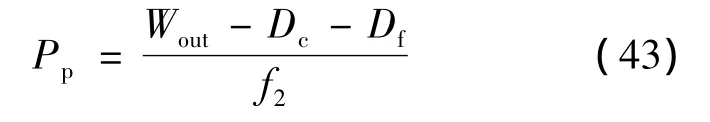
根据上公式可以求出地震被动土压力系数为:

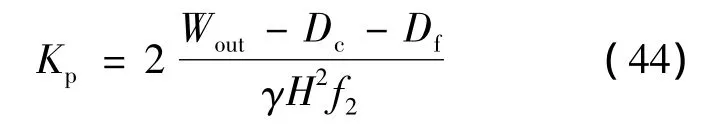
4 计算结果分析

选取适当参数并采用数值计算软件对不同参数下的地震被动土压力系数进行求解计算，分析比较不同的参数对地震被动土压力系数的影响并验证本文计算结果的正确性。图中:Kh为横向地震力系数;Kp为被动土压力系数;c为黏聚力;φ为内摩擦角;rn为孔隙水压力系数。根据图2可以看出，该二级边坡的被动土压力系数Kp随着横向地震力系数Kh，边坡倾角ρ以及孔隙水压力系数ru的增加而增加，随着内摩擦角φ和黏聚力c的增加而减小。在图2(a)中，当ρ=－15°且横向地震力系数Kh=0时，被动土压力系数达到最小值0.236，当 ρ=15°且横向地震力系数 Kh=0.4g 时，被动土压力系数达到最大值0.594;在图2(b)中，当c=20 kPa且横向地震力系数Kh=0时，被动土压力系数达到最小值0.11，当c=0且横向地震力系数Kh=0.4g时，被动土压力系数达到最大值0.931;在图2(c)中，当φ=40°且横向地震力系数Kh=0时，被动土压力系数达到最小值0.232，当φ=20°且横向地震力系数Kh=0.4g时，被动土压力系数达到最大值1.074;在图2(d)中，当ru=0.1且横向地震力系数Kh=0时，被动土压力系数达到最小值0.405，当 ru=0.5 且横向地震力系数 Kh=0.4g 时，被动土压力系数达到最大值0.936。

图2 被动土压力系数随边坡各参数的变化规律Fig.2 Changing rules of passive earth pressure coefficient with parameters of slope

5 结论

1)计算了考虑孔隙水作用的采用挡土墙加固的二级边坡的重力功率、竖向和横向地震力功率及孔隙水做功功率等外力功率和破坏面上的内能耗散、挡土墙与墙后土体黏结力产生的功率及被动土压力功率等内能耗散功率，并根据各功率计算出被动土压力及其系数的上限解的表达式。

2)根据计算出的表达式，选取适当的参数分析不同的参数对被动土压力系数的影响规律:当ρ及横向地震力系数均为最小时，被动土压力系数达到最小值，当ρ且横向地震力系数Kh均为最大时，被动土压力系数达到最大值，当c为最大且横向地震力系数为最小时，被动土压力系数达到最大值，当c为最小且横向地震力系数为最大时，被动土压力系数达到最大值，即二级边坡的被动土压力系数随着横向地震力荷载系数Kh，ρ角和孔隙水压力系数的增加而增加，随着内摩擦角φ和黏聚力c值的增大而减小。

［1］Yang Xiaoli.Seismic bearing capacity of a strip footing on rock slopes［J］.Canadian Geotechnical Journal，2009，46(8):943－954.

［2］王路路，潘秋景，杨小礼.纯黏土坡三维动态上限分析［J］.铁道科学与工程学报，2013，10(2):87 －89.

WANG Lulu，PAN Qiujing，YANG Xiaoli.Three－dimensional upper bound limit analysis for cohesive soil slopes［J］.Journal of Railway Science and Engineering，2013，10(2):87－89.

［3］王路路，潘秋景，杨小礼.三级台阶边坡稳定性分析的上限解研究［J］.铁道科学与工程学报，2013，10(3):43－46.

WANG Lulu，PAN Qiujing，YANG Xiaoli.Upper bound solution for stability analysis of tri－ beaches slope［J］.Journal of Railway Science and Engineering，2013，10(3):43－46.

［4］Nishiyama Taku，Ito Takao.Simplified － three－dimensional slope stability analysis［C］//14th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering，2011.

［5］Khalo K R，Zare N M.The assessment of rock slope instability along the Khosh－Yeylagh Main Road(Iran)using a systems approach［J］.Environmental Earth Sciences，2012，67(3):665 －682.

［6］严若明，周光裕，唐金，等.浅埋隧道塌方机理上限分析［J］.铁道科学与工程学报，2014，11(5):96－99.

YAN Ruoming，ZHOU Guangyu，TANG Jin，et al.Upper bound limit analysis of collapse mechanisms of the shallow tunnel［J］.Journal of Railway Science and Engineering，2014，11(5):96 －99.

［7］许敬叔，潘秋景.盾构隧道开挖面支护力上限分析［J］.铁道科学与工程学报，2014，11(4):80－84.

XU Jingshu，PAN Qiujing.Upper bound analysis of supporting pressure for shield tunnel faces［J］.Journal of Railway Science and Engineering，2014，11(4):80 －84.

［8］杨小礼.岩石极限分析非线性理论及其应用［J］.中南大学学报(自然科学版)，2009，40(1):225－229.

YANG Xiaoli.Limit analysis with nonlinear failure criterion in rock masses and its applications［J］.Journal of Central South University(Science and Technology)，2009，40(1):225－229.

［9］Gharouni N M.The role of instrumentation and monitoring system on the stability of a slope［C］//Harmonising Rock Engineering and the Environment of 12th ISRM International Congress on Rock Mechanics，2012:979 －984.

［10］Bishop A W.The use of pore－pressure coefficients in practice［J］.Geotechnique，1954，4(4):148 －152.

［11］Cecconi，M，Pane V，Napoli P，et al.Deep roots planting for surface slope protection［J］.Electronic Journal of Geotechnical Engineering，2012，17:2809 －2820.

［12］Figueiredo F C，Borges L A，Da Costa L M，et al.Limit analysis for porous materials applied for slope stability analysis［C］//Computational Plasticity XII:Fundamentals and Applications of the 12th International Conference on Computational Plasticity，2013:1319 －1330.

［13］TANG Gaopeng，ZHAO Lianheng，GAO Liansheng，et al.Stability charts for undrained clay slopes in overload conditions based on upper bound limit analysis［J］.E-lectronic Journal of Geotechnical Engineering，2014，19:1531－1537.

［14］YANG Xiaoli，ZHANG Jiahua，JIN Qiyun，et al.Analytical solution to rock pressure acting on three shallow tunnels subjected to unsymmetrical loads［J］.Journal of Central South University，2013，20(2):528 －535.

［15］YANG Xiaoli，YANG Zihan，LI Yongxin，et al.Upper bound solution for supporting pressure acting on shallow tunnel based on modified tangential technique［J］.Journal of Central South University，2013，20(12):3676 －3682.