斜交薄壁连续钢箱梁桥设计与受力特性研究

康崇杰，戴公连，2，粟淼，刘文硕，2

(1.中南大学土木工程学院，湖南 长沙410075;2.中南大学高速铁路建造技术国家工程实验室，湖南长沙410075)

钢箱梁因结构轻巧、易于制造、便于施工，且能较好地适应线路的宽度与高度变化，是中小跨径桥梁最常用的结构形式。该类桥梁一般具有宽度大和梁高小的特点［1－2］。当箱梁与跨越河谷、线路斜交时需要采用斜梁桥结构。目前关于薄壁斜交连续钢箱梁的设计与计算尚有很多不明确的地方。突出表现在以下方面:横隔板布置形式、支承处横隔板传力途径以及斜交钢箱梁锐角区和钝角区的应力分布特征。本文阐述江苏省丹阳路齐梁路某(30+2×35)m跨线斜交钢箱梁的设计特点与设计细节，并对斜交钢箱梁的计算方法进行探讨与分析。

1 斜交钢箱梁设计

江苏省丹阳市，跨越沪宁铁路(30+35+35)m三跨钢箱梁桥为双幅布置，单幅道路总宽为20.9 m，采用顶推法施工以减少对下跨铁路线的影响。横向布置为单向三车道+非机动车道。本桥道路中线与沪宁铁路中线斜交，各墩斜交角度分别为 113°，114°，115°，116°，如图1 所示。

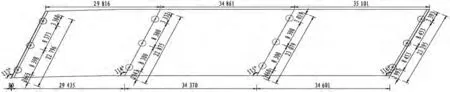
图1 全桥桥跨布置图Fig.1 Bridge span arrangment

1.1 斜交钢箱梁设计特点

1.1.1 横隔板设计

钢箱梁作为一种薄壁箱形结构在偏心荷载作用下，会出现纵向弯曲、扭转、畸变和横向挠曲4种变形［5－7］，实际工程中箱梁要设置横隔板，横隔板的设置也影响箱梁的受力形态［8］。而斜交钢箱梁与普通钢箱梁不同，在设计上最主要的区别是横梁的设置方式，对于普通正交钢箱梁结构一般将横梁与主梁配置成直角。此时横梁与支承线平行，而对于斜交结构，当横梁与主梁配置成直角时横梁与支撑线斜交，简支箱梁可以采用正交或者斜交，而连续梁采用正交布置时，中间墩支承隔板如何布置又是一大问题。一般的斜交钢箱梁横梁配置方案有图2所示3种:正交布置，斜交布置和扇形布置。

图2 横隔板布置图Fig.2 Diaphragm arrangment

斜交钢箱梁桥与正交钢箱梁桥相比，荷载分配表现出明显的空间受力特点，不同的横隔板布置方式必然导致钢箱梁的受力不同。对结构上或经济上究竟哪一种比较好，在日本道路钢桥设计规范第79条中的解释为:板梁原则上与主梁要配置成直角，倘若将板梁配置斜向，对细部结构带来不利，制作也困难，所以即使在斜桥时，也要尽可能将横隔板与主梁配置成直角［9］。同时指出在同样的荷载作用下正交格子梁桥挠度比斜交格子梁桥挠度小，荷重分配正格子比斜格子好;文献［5］指出正交横梁的传力效率好于斜交横梁。除此之外若采用隔板斜交布置，由于钢箱梁道路纵坡和横坡的设置，隔板高度变化各异导致设计制作困难，综上所述最终决定采用正交布置的方案。横板板之间的间距根据经验取为3 m左右。

1.1.2 支承处隔板设计

除在箱梁全桥应布置横隔板之外，在靠近支承处隔板应适当加密，支点横隔板还将承受支座处的局部荷载，起到分散支座反力的作用，一般有如图3所示几种处理方式。

图3 支承处隔板布置Fig.3 Diaphragm arrangment at bearing area

一般横梁隔板厚度均取为14 mm，而在支承处斜向布置横梁均取为30 mm厚。上图所示方案a在支承线上方配置单片横梁，能够起到局部加固作用，结构通过横梁将力传给支座，但是此种布置方式会使斜梁与正交布置隔板相交围成小格子，同时会导致焊缝数量明显增多，斜向横隔板与支座处加劲肋冲突而不宜采用。方案b能够避免方案a的缺点，在保证格子空间最够大的同时尽量减少焊缝且能够避开支座顶端局部加劲肋，是一种值得探讨的科学布置方式。方案c在支承线处配置了2片斜向隔板，能够明显改善横梁受力，但是2块隔板的布置方式会形成一个封闭空间可能导致焊接空间过小，为本桥最终采用的布置方式，在设计时应注意合理布置局部加劲隔板尽量保证足够的工作空间。

1.2 钢箱梁设计细节

1.2.1 箱梁线形控制设计

转坡点桩号K1+370，左侧纵坡为2.2%，右侧纵坡为－2.48%，先跟据转坡点高程计算出各桩号切线标高H0，再据道路勘测相关公式，计算修正值为:

相减得到道路中心线高程设计值

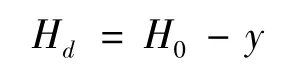
量取内侧边缘目标点距道路中心线的垂直距离x(x为绝对值)，按横坡1.5%计算该点高程为H=Hd－ix。量取横隔板长度d及隔板与道路中心线法线的夹角θ，得到换算横坡i′=icosθ，则外侧边缘点标高为He=H－di′，据此可以求出任意一点箱梁设计标高。

1.2.2 箱梁截面控制设计

箱梁采用单箱多室截面，腹板间距需结合正交异性钢桥面板的跨径以及主梁纵向弯曲时的翼缘有效宽度来确定，顶板采用闭口加劲肋时，正交异性钢桥面板的跨径可达到4～6 m，根据日本《道路桥示方书》对主梁有效宽度的规定，连续梁当单侧翼缘宽度大于跨径的1/20时，翼缘全跨度有效，最终确定采用单箱四室截面，左右侧悬臂长度均取值大于1.75 m，每个箱室宽度大于3.5 m，使翼缘全宽有效。本桥梁高取为2 m左右，考虑到取2%的横坡以及线路纵坡因素，最后取值为箱梁最内侧腹板高度为2 456 mm，最外侧腹板高度为2 203 mm，中间腹板高度通过直线插值求得。

1.2.3 箱梁纵肋设计

钢箱梁的顶底板宽度较大，设置纵横加劲肋是防止顶底板在弯曲压应力或者制作、运输、安装架设中在不可预料的压应力作用下局部失稳的最有效方法［10］。纵肋采用闭口截面肋较之开口截面肋抗扭具有更大的刚度和屈曲稳定性。考虑到顶板局部承受汽车轮压，底板承受较大支座反力且连续梁在中间支承处底板受到较大反弯矩，从提高钢桥面板的刚度出发，采用8mm厚的梯形闭口肋，在靠近腹板处和设置排水孔侧翼缘辅之以开口截面I字肋，开口肋板厚约为 10 ～25 mm［11－12］，本桥取为18 mm。并保证顶板U肋间距不大于600 mm，底板U肋间距不大于800 mm，I字肋间距不大于400 mm。

1.2.4 箱梁板厚设计

为防止顶底板刚度过小导致桥面铺装过早破坏，以及承受车轮局部荷载，底板最小厚度一般不小于12～14 mm，底板厚度不小于10 ～12 mm［9］，为保证安全，本桥全桥取顶板厚度为16 mm，底板厚度为14 mm，由于在中间墩支承处产生反弯矩产生压应力且需要承受支座局部应力，在支座两侧范围16 m内底板加厚为25 mm设计。最终确定本桥跨中标准断面如图4所示。

图4 跨中标准断面Fig.4 Standard section

2 模型分析

2.1 模型建立

常采用的计算分析方法包括单梁法、梁格法与板单元法，选用哪种计算方法对此类钢箱梁进行计算分析较为科学、安全是值得研究的问题。目前，单梁法仍广泛应用与混凝土桥梁及钢结构桥梁的设计计算中，该方法的特点是能够直接计算截面的内力和变形。梁格法是一种空间计算的近似方法，其核心思想是利用等效的纵、横梁格代替桥梁上部结构，将分散在板、梁每一区段的弯曲刚度和扭曲刚度集中于最邻近的等效梁格内，能够模拟桥梁的横向受力状态。板单元法是利用板单元来模拟箱梁结构的上翼板、下翼板、腹板、横隔板纵向加劲肋等，可以分析任何复杂形状的结构［3－4］。本桥分别采用上述3种方法对桥梁受力特性进行分析。

2.1.1 单梁法模型

桥梁纵向长度大于横向宽度，荷载使桥梁上部沿纵向产生弯曲和扭转而横向不改变形状时，桥梁上部结构可以作为一根梁考虑。采用Midas Civil 2010建立单梁模型，如图5所示，全桥共划分为102个单元和103个节点。单梁法只能建立直梁模型，且无法考虑箱梁横向受力状态，如图5(b)所示纵向加劲肋根据箱梁实际纵肋布置情况进行准确模拟，横向隔板以及局部缀板等结构的重量通过改变材料自重系数进行调整。

图5 钢箱梁单梁计算模型Fig.5 Single－beam model

2.1.2 梁格法模型

斜交钢箱梁为单箱四室截面，计算中将箱梁沿横桥向离散为5根纵梁，分别编号为a，b，c，d和e，全桥共划分为232个节点，369个单元(如图6所示)。本桥实际为整体箱梁，根据实际位置及厚度模拟横向隔板和纵肋布置情况，确保全桥较好的横向联系。利用Midas2010建立梁格模型，如图7所示。利用梁格可以模拟斜梁构造，与箱梁实际空间结构尽量保持一致。根据支座实际布置情况，固定支座约束纵桥向、横桥向、竖桥向3个方向位移，单项活动支座约束横桥向(或纵桥向)、竖桥向位移，双向活动支座只约束竖桥向位移，分析支座反力的空间分配，考虑箱梁的横向受力情况。箱梁截面特性应进行等效计算，其中横向剪切刚度对横向受力产生较大影响，其等效计算公式为:

其中:As为构件等效剪切面积(包括横隔板面积);d′，d″，dw和 h分别表示顶底板宽度、腹板宽度以及腹板厚度。

图6 钢箱梁梁格划分示意图Fig.6 Schematic diagram of grillage

图7 钢箱梁梁格法计算模型Fig.7 Grillage model

2.1.3 板单元模型

采用通用有限元软件ANSYS建立全桥板单元模型，模型中结构横隔板和加劲肋等的尺寸和位置完全与施工图纸一致，钢桥各面板采用8节点shell91非线性壳单元模拟，加劲肋采用空间梁单元beam44模拟。全桥共划分为59 292个单元和129 744个节点，全桥有限元模型如图8所示，板单元能够模拟箱梁的实际空间结构，纵向加劲肋与横隔板均能够根据实际情况进行模拟。

2.2 结构分析计算

2.2.1 支座反力

采用单梁法计算时只能得出每个墩顶支座反力之和，而无法分别得出每个支座的反力。然而由于箱梁存在横坡而且该桥整体为斜梁结构，同一墩顶的3个支座反力必然会产生较大差异，在极端的情况下甚至出现某一支座脱空，产生负反力的情况，而采用梁格法和板单元计算可以精确地模拟出支座的实际位置得出每一个支座的反力。3种计算方法各支座反力对比见表1，表中梁格法与板单元同一墩顶支座从内向外分别编号为1，2，3。从表1可以看出，恒载活载作用下单梁法、梁格法和板单元法支座反力计算结果较为接近，均在计算误差范围之内，而其中梁格法计算支座反力＞单梁法支座反力＞板单元法支座反力。梁格法趋于安全。且在17号墩与18号墩墩顶，梁格法与板单元法支座反力均为支座2＞支座1＞支座3，支座反力具有相同的分配趋势，但是板单元法计算反力分配更加平均而梁格法计算反力分配差别较大，这是由因为采用梁格法计算时，为保证重心位置与整体模型一致划分单元时可能造成支座偏心受压而导致单个支座反力偏大或偏小。这种现象在16号墩与19号墩时这种现象更为明显，板单元计算结果更加精确。

表1 支座反力对比Table 1 Comparison of supporting force

图8 钢箱梁板单元计算模型Fig.8 Plate model

2.2.2 结构变形分析

进行变形分析时，单梁法能够计算得出全桥纵向挠度分布，梁格法计算模型计算得出模型每一根纵梁和横梁挠度分布，而板单元计算模型计算得出全桥任意位置的挠度分布。最大活载效应下3个模型挠度分布如图9所示。

其中3种计算模型在最大活载作用下的挠度计算结果如图10所示。

图9 最大活载下箱梁挠度Fig.9 Deformation under traffic load

计算结果表明，板单元计算挠度大于梁格法计算挠度，梁格法计算挠度大单梁法计算挠度。这是由于板单元计算精度大于梁格模型，而梁格模型单元划分精于单梁模型且用单梁法分析时由于单元划分受限制无法考虑桥梁局部受力较大时产生的挠度。如图9所示3种计算模型最大挠度均产生于最右跨跨中，如图9(b)梁格模型最大挠度产生与最外侧纵梁，中间纵梁最大挠度最小。如图9(c)板单元模型计算最大挠度同样产生与最外侧位置。单梁法挠度计算结果单梁法最小，而板单元法计算最大，梁格法计算结果介于上述两者之间。

图10 3种计算模型挠度对比Fig.10 Deformation comparison of three models

2.3.3 全桥纵向应力分析

单梁模型以及梁格法计算模型均为梁单元计算模型，在用Midas2010进行应力计算时只能够计算得出梁单元梁顶和梁底的应力大小。用ansys建立板单元模型计算时能够得到每一个板单元板顶、板底以及中性面任意位置应力大小及分布状态。在最大包络荷载作用下各模型纵向正应力计算结果如图11所示。

如图11所示单梁模型，梁格模型以及板单元模型纵向最大应力均产生于18号墩支座处，且3种模型应力分布曲线具有相似的趋势。最大应力值分别为单梁54.9 MPa＜板单元模型100.0 MPa＜梁格模型107.8 MPa。由此可见，采用单梁模型计算斜交钢箱梁过于粗糙，纵向应力偏小趋于不安全，而采用梁格法与板单元计算时纵向应力结果较为接近且梁格法计算稍偏大。

2.3.4 横隔板横向应力分析

采用单梁法建立箱梁的有限元模型不能考虑荷载的横向分布，而梁格法和板单元法均可以考虑荷载横向效应，故本节只对梁格法与板单元法进行分析对比。其中箱梁端横为单隔板结构，而中横梁为双横隔板结构。

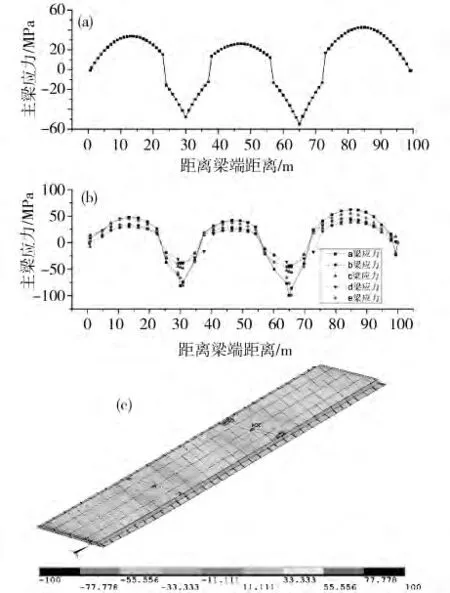
图11 最大包络荷载作用下全桥应力分布Fig.11 Longitudinal stress distribution

图12 隔板应力Fig.12 Side－diagram stress distribution

如图12所示，采用梁格模型计算16和19号墩顶斜横隔板最大正应力分别为118.2 MPa和143.0 MPa。采用板单元模型计算16和19号墩顶斜横隔板最大正应力分别为102 MPa和150 MPa。Ansys计算结果稍大于梁格法模型，由图12(c)和12(d)可以看出隔板总体应力状态较低，且基本小于40 MPa，而在支座位置附近隔板应力明显增大，这是由于支座局部承压较大所致。由此可知总体计算梁格法偏于安全，但是板单元计算更趋于细致能够考虑在局部较小区域的应力集中现象。上述现象同时表明，支承处横隔板传力途径为箱梁作用先通过腹板传递到横梁，横梁再把梁内分散的力集中传递给支座，再由支座传递给下部结构。

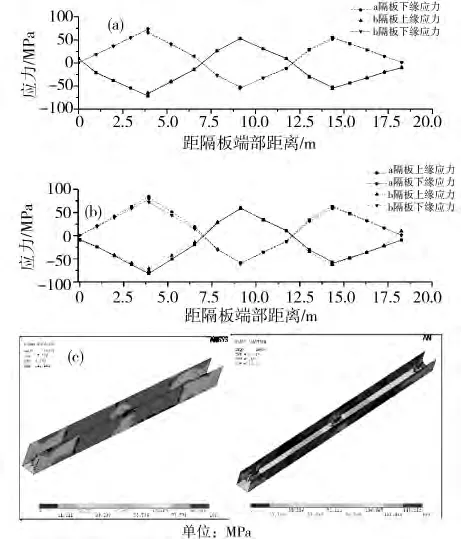
图13 中横隔板应力Fig.13 Mid － diagram stress distribution

如图13所示，梁格法与板单元计算应力分布结果具有相似的分布规律，在腹板与隔板相接处达到最值。梁格法计算得出17号和18号墩顶横隔板最大应力分别为72.9 MPa，84 MPa，而板单元法最大应力分别为88.9 MPa和142.22 MPa。与16号和19号墩顶隔板应力结果类似，隔板总体应力梁格法计算结果偏大趋于安全，但是在支座局部承压区域内的计算结果板单元计算结果更大趋于安全。

2.3.5 斜交钢箱梁锐角区和钝角区的应力分布特征

斜交钢箱梁在恒载和恒载+活载包络的作用下其4个角点(如图14所示)的应力值如表2所示。

图14 角点示意图Fig.14 Angular point diagram

表2 钢箱梁锐角、钝角区等效应力Table 2 Stress in different angular zones MPa

如表2所示，在恒载和恒载+活载包络作用下1.56≤J2/J1≤2.88，1.51≤J4/J3≤3.64，即同种工况下钝角区应力大于锐角区应力，这是钝角区域支座反力大于锐角区支座反力导致的。

3 轮压荷载局部分析

考虑在车辆荷载作用下，35 m跨中截面桥面板和跨中截面内侧翼缘板的局部受力情况。计算模型采用全桥壳单元模型，车辆轴重P=140 kN，轮压 q=P/(2×800×400)=0.22 MPa。纵向加载有效宽度为0.8 m，横向加载宽度为0.4 m，横向加载位置如图15所示。

图15 轮载加载Fig.15 Wheel load icon

在轮压荷载作用下，桥面板的纵向正应力和局部变形见图16～17。如图16～17所示，在轮压局部荷载作用下最大挠度为1.604 mm，最大应力为29.03 MPa均在允许范围之内，结构安全可靠。

图16 桥面板变形Fig.16 Deformation of deck

图17 桥面板纵向正应力σxFig.17 Stress of deck

4 结论

1)提出了斜交钢箱梁横隔板的正交布置方式。

2)单梁法各项纵向计算偏于不安全，且无法进行横向分析计算，无法得出反力、应力等的沿横桥向计算结果。梁格法与板单元均能够进行横向计算分析，2种方法计算结论较为相近，且总体上梁格法计算结果更偏安全。对于较宽的箱梁以及斜梁应采用梁格法或板单元法进行计算，以便得到支座以及应力等沿横桥向分布，为支座布置以横向设计提供理论依据。

3)板单元模型计算更为细致精确，能够对模型进行局部受力分析，最为接近真实状态，但由于计算复杂，设计中较少采用。对于局部承压较大的钢箱梁应采用板单元法进行局部分析，可以确定局部承压构件的安全性。

4)同种工况下斜交钢箱梁钝角区应力大于锐角区应力。

5)轮压局部荷载作用下，本桥桥面板变形、应力均远小于规范限制，结构安全可靠。

［1］吴冲.现代钢桥［M］.北京:人民交通出版社，2011.

WU Chong.Modern steel bridge［M］.Beijing:China Communications Press，2011.

［2］徐君兰，孙淑红.钢桥［M］.北京:人民交通出版社，2011.

XU Junlan，SUN Shuhong.Steel bridge［M］.Beijing:China Communications Press，2011.

［3］李慧华.扁平薄壁钢箱梁计算方法研究［D］.西安:长安大学，2010.

LI Huihua.Study on the calculation method of thin －walled steel box girder［D］.Xi’an:Chang’an University，2010.

［4］兰枢灵.薄壁钢箱梁计算方法研究［D］.西安:长安大学，2011.

LAN Shuling.Study on the calculation method of thinwalled steel box girder［D］.Xi’an:Chang’an University，2011.

［5］项海帆.高等桥梁结构理论［M］.北京:人民交通出版社，2013.

XIANG Haifan.Advanced theory of bridge structure［M］.Beijing:China Communications Press，2013.

［6］何旭辉，封周权，陈政清，等.基于混合有限元法的钢箱拱相关稳定分析［J］.铁道科学与工程学报，2007，4(6):7－11.

HE Xuhui，FENG Zhouquan，CHEN Zhengqing，et al.Interactive stability analysis of steel box arch ba sed on mixed finite element method［J］.Journal of Railway Science and Engineering，2007，4(6):7 －11.

［7］周凌宇，贺桂超.考虑界面滑移的多自由度钢－混组合箱梁空间有限梁段法［J］.铁道科学与工程学报，2012，9(4):1－7.

ZHOU Lingyu，HE Guichao.Finite segment method for steel－concrete composite box beam with multi－degreeof－ freedom considering slip［J］.Journal of Railway Science and Engineering，2012，9(4):1 －7.

［8］李海锋，罗永峰.横隔板对薄壁钢箱梁纵向正应力的影响［J］.建筑结构学报，2010(S1):39－44.

LI Haifeng，LUO Yongfeng.Influences of diaphragms of thin－walled box steel beams on longitudinal mormal stress［J］.Journal of Building Structures，2010(S1):39－44.

［9］高岛春生.斜梁桥［M］.北京:中国建筑工业出版社，1978:31－35.

Takashima Chunsheng.Skew bridge［M］.Beijing:China Building Industry Press，1978:31 －35.

［10］Chai H Y，Byung H C，Elizabeth M F.Stiffness requirement for longitudinally stiffened box － girder flanges［J］.Journal of Structure Engineering，2001，127(6):705 －711.

［11］李立峰.正交异性钢箱梁局部稳定分析理论及模型试验研究［D］.长沙:湖南大学，2005:28－31.

LI Lifeng.The analytical theory and model test research on local stability of orthotropic;steel box girder［D］.Changsha:Hunan University，2005:28 －31.

［12］李立峰，邵旭东.扁平钢箱梁闭口U形加劲板屈曲特性理论分析［J］.公路交通科技，2008，25(3):88－92.

LI Lifeng，SHAO Xudong.Theoretical analysis plate stability property of U－rib stiffened flat steel box girder［J］.Journal of Highway and Transportation Research and Development，2008，25(3):88 －92.