基于Contourlet变换的遥感图像融合方法研究

李文静，温文鹏，王清和

(1．江西省煤炭工业科学研究所，南昌 330029;2．苏州科环环保科技有限公司，苏州 215301)

0 引言

随着遥感技术的快速发展，人类不断获得对地观测的海量数据。由于传感器设计的局限性，遥感图像的空间分辨率与光谱分辨率是一种逆相关关系［1］。由于应用目的不同，单一传感器获得的图像往往不能满足某些具体的要求，图像融合技术作为克服单一数据局限性的重要方法日益引起了人们的重视［2－3］。

20世纪80年代，文献［4－6］中将IHS变换应用于多源数据处理和图像增强，但IHS方法扭曲了原始的光谱特性［7－8］。20世纪90年代，小波变换(wavelet trensform，WT)多尺度分析代替了传统的塔式算法［9－14］。Zhou 等［9］在文献中列举了应用 WT进行多源图像融合的常用方法。为改进融合效果，研究人员对WT的融合规则进行了广泛研究［10－14］。宋杨等［10］提出了一种自适应的基于局部小波系数特征的遥感图像融合方法，该方法有效地减轻了图像的光谱失真，提高了融合图像与源图像的相关性。Kim［11］等提出了改进的加性多孔小波融合方法，针对边界问题提高了空间细节信息，使量化指标得到了较大提高。蔡娜［12］提出了一种基于区域相似度的小波系数融合方法，将区域相似度的思想应用于图像融合规则中，避免了只考虑一个特征量作为融合结果判决标准的缺点。实验证明，上述方法突出了地物的结构性，有效地增强了图像的整体感;但多数研究采用的融合规则并未从根本上改善融合信息的特征，融合算法显露出存在信息丢失的严重缺陷。2000年Do等［15］提出了轮廓波变换(Contourlet transform，CT)，亦称“金字塔型方向滤波器组”［16－18］。由于Contourlet基的支撑区间(不同分辨率条件下的不同尺寸的长条形结构)具有随尺度变换的特性，对细小的有方向的轮廓和线段具有独特的表达优势，因此该变换在图像融合中能够有效地提取细节信息［19］。Mahyari等［20］提出了一种基于 CT 的光谱分辨率和空间分辨率最大化的图像融合方法，使用表征不同频率域光谱的光谱直方图以及四阶精度相关系数作为融合规则，但融合过程中的阈值设置问题影响着融合效果。Cunha等［21－23］提出的改进非采样CT方法不同于经典的CT方法需进行上、下采样器的采样处理，而是先将图像经过滤波器进行上采样，然后针对该上采样获取的信号进行分解和重构，从而使得滤波后图像信息不会由于使用上、下采样器而导致错位，可以更好地提取图像的细节纹理信息，但未从融合规则上作出改善。Kong等［24］提出了基于非下采样CT(nonsub sampled CT，NSCT)与IHS变换的可见光与红外灰阶图像的融合技术，综合了传统的IHS变换及CT的优势。由于NSCT具有平移不变性，在保持图像细节方面效果显著;然而相对于传统CT方法，NSCT具有较高的信息冗余。

本文以“从全色图像中提取当前多光谱图像不具备的空间细节信息、在多尺度小波分析框架下将其融入多光谱图像”为研究目标，基于多尺度WT［25］及CT，进行图像的分解和重建;结合传统的IHS变换方法，提出了一种基于CT变换的遥感图像融合方法，有效地达到了将全色图像的空间细节信息融入多光谱图像的目的;并采用信息熵、标准差、相关系数和光谱畸变度等指标对融合结果进行评价。实验结果表明，与传统方法相比，该方法在保持多光谱图像光谱信息的同时，有效地提高了图像的空间分辨率。

1 CT变换基本原理

WT的多尺度分析为图像的空间尺度分析提供了统一的框架，其多尺度分析特性使得融合结果保留了较为丰富的高频细节信息。但对于二维图像或更高维的图像数据，WT的稀疏表示能力比较有限［15－16］。二维可分离小波基函数的支撑区间是一个正方形(图1(a))，最终表现为以“正方形点”来逼近线的过程，且各向同性，能准确地表示二维或者高维信号在竖直、水平或对角线方向的直线奇异性。

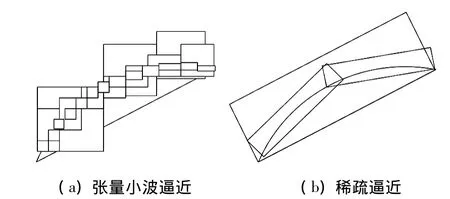
图1 奇异曲线的不同逼近方式Fig．1 Different approximation ways to singular curves

然而，遥感图像中多数地物具有平滑的边缘，使得其奇异点往往不是独立分布的，而是聚集成具有某些几何特征的奇异曲线。在这种情况下，WT的各向同性的基函数不能有效地利用数据本身特有的几何特征捕捉图像中沿边缘方向的曲线奇异。而CT是近年来推广的一种多尺度几何分析方法，具有各向异性特征，较好地解决了WT不能有效表示的边缘和轮廓等高维奇异问题，在一定程度上改进了基于WT融合算法中边缘和纹理信息的保留状况。

CT变换也称为金字塔形方向滤波器组(pyramidal directional filter bank，PDFB)，是一种多分辨率的、局域的、带方向的图像表示方法。它的Contourlet基的支撑空间具有随尺度改变而长宽变化的“长条形结构”(图1(b))，因此能够更好地表现边缘特征，更适合于进行多尺度边缘的增强处理［23］。

CT变换的实现主要包括2个分解步骤:①拉普拉斯金字塔(Laplacian pyramid，LP)分解;②方向滤波器组(directional filter bank，DFB)滤波。其合成变换过程正好相反(基本过程见图2)。

图2 CT示意图Fig．2 Sketch map of CT

其中，拉普拉斯金字塔分解通过对原始图像进行一系列的下采样(即二次采样(subsampling))、高斯平滑及相邻层次之间的图像减运算得到图像的拉普拉斯金字塔，从而实现图像的多尺度分析;再利用方向滤波器组对图像的拉普拉斯金字塔各带通子带进行方向分解，从而有效地捕获各带通子带的方向信息。

2 基于CT和IHS变换的融合方法

研究全色图像与多光谱图像的融合是为了在保持原始多光谱图像光谱信息的同时，有效地融入全色图像丰富的空间细节信息，从而获得空间分辨率和光谱信息保持俱佳的“双高图像”。

2．1 IHS变换与光谱质量

亮度－色度－饱和度(intensity－hue－saturation，IHS)彩色空间变换是一种经典的将高分辨率图像结构信息融入到低分辨多光谱图像中的融合技术。图像从RGB到IHS彩色空间的转换的同时，在一定程度上实现了包含图像结构信息(I)与光谱信息(H和S)的分离，从而使后续算法中通过只对亮度分量(I)进行处理获得丰富结构信息的同时，减少对光谱信息的改变，有效保证图像的光谱质量。

2．2 CT变换与空间质量

CT的多尺度分析和多方向分析分开进行的“长条形结构”，相对于第一代WT的多尺度“正方形”各向同性而言，具有更稀疏的空间细节表达能力，可以提取更丰富的空间信息。CT是WT的一种新扩展，在任意尺度上能分解成2的任意次方个方向子带，具有多方向性(图2)，能更好地恢复图像的空间纹理信息。

2．3 CT 融合规则

在传统的WT得到的不同尺度分量信息中，低频分量集中了较多的光谱信息，高频分量则为细节纹理信息。WT融合的基本原则是低频分量尽可能地保留多光谱图像的光谱特征，高频部分则增加空间细节信息。然而CT因其多尺度和方向分析的分开独立进行，因此相对于第一代WT具有更稀疏的空间细节表达能力;而在光谱质量的保持上，能够获得与第一代WT很接近的融合效果。但传统的基于CT融合方法的研究大多采用的是不同频率信息之间的替换，并未从根本上改善融合规则。为此，本文结合IHS变换、针对CT处理得到的不同尺度分量采用“低频自适应、高频基于区域相似度”的融合规则，进行基于局部小波系数的遥感图像融合算法研究。

2．3．1 低频分量的自适应融合

如前所述，为了尽可能地保留原始多光谱图像的光谱信息，低频分量融合应尽可能更多地采用多光谱图像的光谱特征，同时将全色图像的纹理特征融入到多光谱图像中。其具体的融合方法如下:

1)提取fmul－I和fpan的低频分量所共有的特征，即

2)提取全色图像低频部分所特有的特征，即

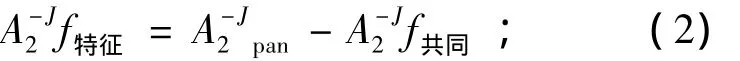
3)生成融合图像 I分量低频部分A－J2fnew－i，即

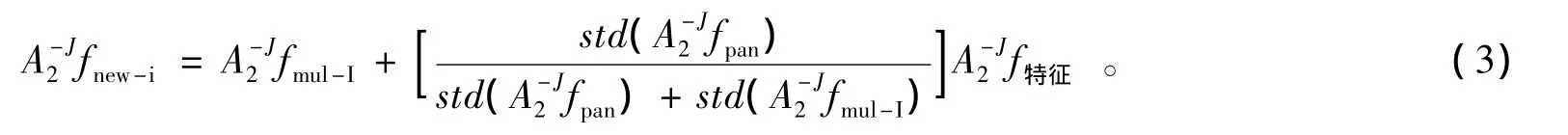
2．3．2 高频分量的融合

高频分量要尽量融入原始全色图像的空间细节信息，而细节信息在图像中更多地体现为纹理或图斑的结构等。一般图像具有很强的结构性，像素之间也存在很强的相关性，而这些相关性蕴含着图像结构的重要信息。在人眼对图像信息提取过程中，结构信息是识别地物的重要特征，因此图像结构是度量图像感知信息质量的最好近似［23］。Wang［26］等于2002年首次提出了结构信息的概念。本文将“结构性”思想引入遥感图像高频细节信息提取融合规则中，把“结构相似度”作为一个测度，设定一个阈值，然后分别针对不同的相似度进行不同的处理。此外，方差也作为信息密度的量度应用于本算法。数理统计中对方差描述的是数据的分散程度，方差越大，说明数据的越分散;而在图像数据中，方差越大表明图像的像素变化越大，表现为图像的细节、边缘特征越明显。本文在高频融合规则中，采用了阈值控制结构相似度准则，实现了有选择地对多光谱图像和全色图像的高频分量进行区域方差最大取值或加权平均融合。

2．3．3 结构相似度

2景图像X和Y之间结构相似度(structural similarity，SSIM)定义为

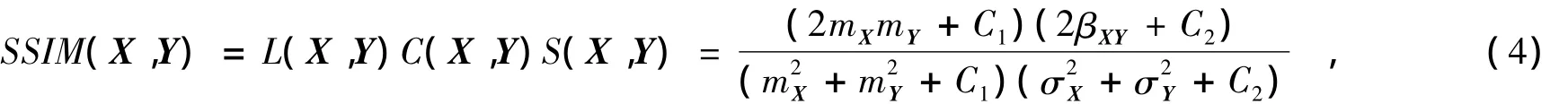
其中

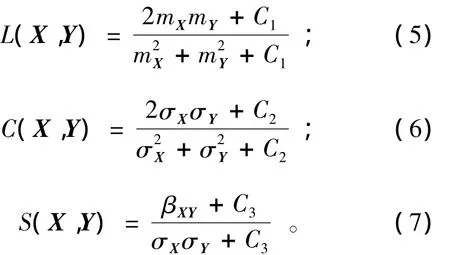
式(4—7)中:mX和mY分别为图像X和Y的均值;和分别为图像X和Y的方差;βXY为图像X和Y的协方差;L(X，Y)为图像X和Y的亮度比较;C(X，Y)为图像X和Y的对比度比较;S(X，Y)为图像X和Y的结构比较;C1，C2和C3为常量(为避免式中分母为0而导致算法不稳定)。

SSIM是度量2景图像结构相似度的一个指标，它反映了2景图像的相关性，并且其值在［－1，1］之间:取值为1时，表示2景图像的模式完全一致;取值为－1时，表示2景图像的模式完全相反。

本文首先定义一个阈值ρ，用于确定高频系数融合的方式;然后对多光谱图像和全色图像的高频部分做窗口运算，计算其对应的区域相似度，并记录相似度的值;接着对不同的情况进行不同的处理:当相似度小于ρ时，采用方差最大原则进行融合;否则，采用“加权平均”方式进行融合，即

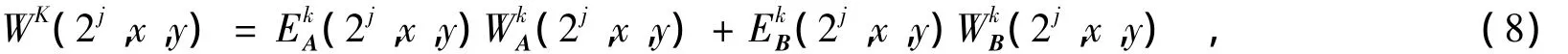
其中

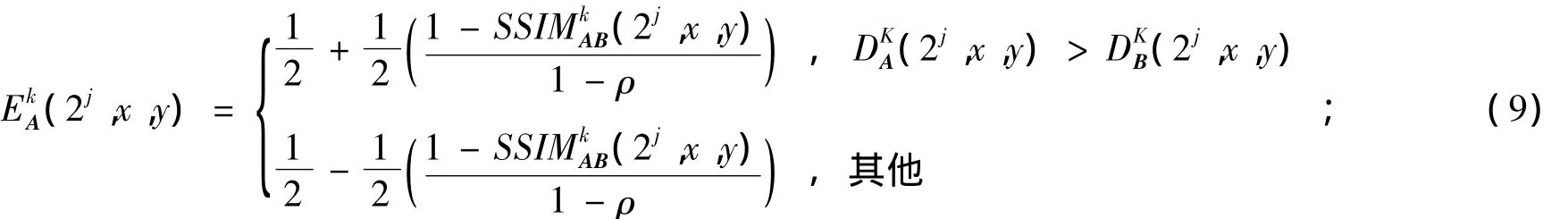
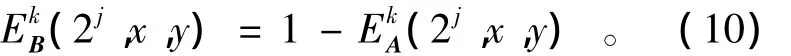
式(8—10)中:ρ为设定的阈值(实验中取ρ=0．5);WK(2j，x，y)为融合结果图像的高频细节分量,(2j，x，y)和(2j，x，y)分别为图像 A 和图像 B的高频细节分量;(2j，x，y)和(2j，x，y)分别为图像A和图像B的权重值;(2j，x，y)和(2j，x，y)分别为图像A和图像B某一窗口中的方差。

当2景源图像的对应区域结构相似度小于一定阈值时，说明2景图像差别较大、相关性较小，则采用“方差最大”融合，可以保留2景图像中的主要细节信息;否则，说明2景图像比较相似，采用“加权平均”融合。

2．4 本文的改进算法

结合传统图像融合方法，利用CT在空间细节提取上的优势，有针对性地改进不同分量间的融合规则是本文提出算法的主要改进。通过IHS分量替换算法得到包含图像丰富空间特征的亮度分量，然后分别对该亮度分量与全色图像进行CT变换得到对应的低频分量及高频分量。在融合规则的选择中，本文采用“低频自适应、高频区域相似度阈值控制”融合规则。实验结果表明，该方法与传统方法相比，在整体效果上较优。具体步骤如下:

1)对原始全色图像和多光谱图像进行高精度几何配准，配准精度要求在1个像素以内;并对多光谱图像进行重采样，使之与全色图像大小相同;

2)对多光谱图像进行从RGB空间到IHS空间的转换，得到代表亮度的分量I和其余的色度(H)分量和饱和度分量(S);

3)分别对多光谱图像的亮度分量和全色图像进行CT变换，从而得到相应的不同分辨率、不同方向上的CT变换低频分量系数和高频分量系数;

4)对获得的低频分量系数采用前文提到的低频自适应的融合规则进行融合，得到新的低频分量;而对高频分量则根据分解层次进行有选择地融合:对于普通高频部分(除最高频次高频部分——本文称之为“最精细高频部分”外)，当多光谱图像亮度分量的系数绝对值大于全色图像时，融合系数取二者系数的代数和，否则直接取全色图像的系数值;而对于最精细高频部分，则直接取全色图像的最精细部分系数值;

5)对融合得到的低频分量和对应的高频分量进行Contourlet逆变换，得到新的亮度分量;

6)将得到的亮度分量与步骤2)中的色度分量和饱和度分量进行IHS逆变换，得到最终的融合结果图像。

3 实验结果与分析

本文采用ENVI软件中自带的英国伦敦地区图像——SPOT全色图像(图3(a))和 Landsat卫星TM多光谱图像(图3(b))进行融合实验，其中SPOT全色图像空间分辨率为10 m，TM多光谱图像空间分辨率为28m;实验用图像大小均取256像元×256像元。实验过程中，对比WT采用的小波基为dbN系列(如db 13)，小波分解层数为3。

采用5种典型的图像融合方法进行了实验对比与分析:①IHS变换融合［5］;②基于IHS的WT融合［9］;③传统的基于IHS与CT高频分量替换的融合;④非下采样CT(NSCT)融合［24］，其中低频子带采用自适应策略，高频子带利用偏差系数及信息熵融合判别策略;⑤本文改进的CT(I－CT)融合。5种融合方法的图像融合结果见图3(c)—(g)，图中红框部分为目标区域(即目视对比的关键区域)。

图3 系列融合结果Fig．3 Fusion results of different algorithm s

为了对比评价不同融合方法的融合效果，本文不仅从目视效果进行直观比较，并对融合结果进行了定量指标评价分析，主要包括光谱保持特性及对图像信息量的对比评价。其中，对光谱保持质量的评价指标采用相关系数(CC)、光谱畸变度(SDD)和灰度均值(M);对图像信息量则通过信息熵(IE)和标准差(SD)来衡量。

通过对实验结果的目视比较可以看出，相对于TM图像(图3(b))，除 IHS变换融合结果(图3(c))出现了明显的光谱扭曲之外，基于WT(图3(d))及CT(图3(e))变换的融合算法均实现了在“保持光谱信息的同时，有效改进空间分辨率”的目标，即在光谱畸变不大的情况下，空间细节信息明显较原TM图像(图3(b))丰富。WT融合算法获得的融合结果(图3(d))光谱畸变度较低，但是图像比较模糊，空间分辨率改变不明显;而CT方法相对于传统的第一代WT，由于采用了不同的奇异曲线逼近方式，在空间信息的提取方面，捕获了图像中存在的丰富的、更多的方向信息，从而在空间细节的保持上优势明显(图3(e)(f)(g))。但是，由于CT分裂层数多、方向滤波器密集程度高，使得获取的结构细节信息较冗余，在目视效果上出现所谓的“虚景”情况(图3(f)最为明显)。

尽管传统的CT及NSCT融合方法在纹理细节信息的保持上表现出明显的优势，但是，CT变换融合图像(图3(e))中的“虚景”表现出明显的吉布斯效应(Gibbs effect);而NSCT变换融合图像(图3(f))虽然在空间细节的提取上较好地发挥了“平移不变性”的优势，该算法设计中高频分量基于偏差系数及信息熵的融合规则在保持局部空间细节上效果显著，但无法更多地顾及空间结构信息。用本文提出的方法得到的融合图像(图3(g))在减小光谱退化的基础上，有效地顾及了图像中地物的空间分布及结构信息。

表1列出5种方法融合图像质量的评价指标。

表1 不同方法融合图像质量的评价指标Tab．1 Evaluation indexes of quality for images fused by using different methods

从表1可以看出，在图像信息量方面，基于IHS变换融合方法的融合图像的信息熵最大(7．86)，I－CT的次之(7．70)，而 WT，CT及 NSCT的较小。这说明融合方法相同、但融合规则不同会导致有较大差异的融合效果。从图3(f)的细节信息以及表1中NSCT的标准差及信息熵指标中可以看出，基于SSIM的融合规则更有助于提高融合图像的高频细节信息。同样，在信息熵指标中，本文的改进方法仅略低于IHS变换融合方法，能获得较大的信息量。

在光谱信息的保留方面，对照TM多光谱图像RGB波段的均值和光谱相关系数及畸变度进行分析。WT方法融合图像的均值与TM图像的最接近，IHS方法融合图像的均值与TM图像均值的差距最大，反映出IHS方法的光谱退化是最明显的。同时，相关系数和光谱畸变度指标进一步表明，WT融合算法与I－CT算法能更好地保证融合图像的光谱质量。但相对于 TM图像，I－CT算法的融合图像(图3(g))存在微弱的光谱扭曲;究其原因，可能是在CT过程中，对多光谱图像的拉普拉斯变换使得最终参与高频融合的光谱信息比WT的增多，而低频分量中的光谱信息保留相应减少，最终导致基于CT融合方法出现微弱的光谱畸变。

4 结论

1)本文利用标准的IHS变换，结合传统多尺度小波变换(WT)方法，对比研究了具有多分辨率、多方向、更具稀疏表达能力的第二代轮廓波变换(CT)在多源遥感图像融合中的应用。具体研究了基于IHS的改进CT算法，结合传统IHS变换，将经IHS空间变换获得的亮度分量与原全色图像均进行CT，发展了一种基于“低频分量自适应、高频基于区域相似度的阈值控制”的融合规则，分别对CT得到的高低频分量进行融合操作，最后再经过一系列逆变换得到最终的融合结果图像。

2)从实验结果的目视效果上来看，基于CT的融合方法与基于WT的融合方法在结构细节信息和光谱信息的表现能力上相当。与此同时，为了能对融合图像质量进行定量的分析，本文还采用了均值、标准差、信息熵、相关系数以及光谱畸变度等评价指标。这几个指标是对光谱信息畸变的度量，而标准差和信息熵则反映了图像信息量的大小。通常情况下，融合图像的空间分辨率和光谱分辨率很难同时达到最佳的效果，由于CT在空间细节信息保持上的优势以及针对光谱保持设计的低频自适应融合规则的使用，本文提出的融合方法在定量指标综合显示中较优。

3)由于CT分裂层数以及其方向滤波器的密集程度，空间细节信息在保持上较为冗余，融合结果图像的吉布斯效应显著。因此，未来的工作将集中于寻找消减第二代WT中吉布斯效应的策略，实现对空间结构信息更加有效的表达。

［1］ Gonzalez－Audicana M，Saleta J L，Catalan O G，et al．Fusion of multi spectral and panchromatic images using improved IHS and PCA mergers based on wavelet decomposition［J］．IEEE Transactions on Geoscience and Remote Sensing，2004，42(6):1291－1299．

［2］ 褚进海，彭 鹏，李 郑，等．矿山遥感监测中QuickBird数据融合方法研究［J］．国土资源遥感，2009，21(3):107－109．doi:10．6046/gtzyyg．2009．03．21．Chu JH，Peng P，Li Z，et al．The fusion method for Quick Bird data inmine remote sensing monitoring［J］．Remote Sensing for Land and Resources，2009，21(3):107－109．doi:10．6046/gtzyyg．2009．03．21．

［3］ 于海洋，甘甫平，邱振戈．CBERS－02B星数据融合方法评价［J］．国土资源遥感，2009，21(1):64－68．doi:10．6046/gtzyyg．2009．01．14．Yu H Y，Gan F P，Qiu Z G．Data fusion evaluation of CBERS－02B［J］．Remote Sensing for Land and Resources，2009，21(1):64－68．doi:10．6046/gtzyyg．2009．01．14．

［4］ Welch R，Ehlers M．Merging multire solution Spot HRV and Landsat TM data［J］．Photogrammetric Engineering and Remote Sensing，1987，53(3):301－303．

［5］ Carper J T M，Lilles and T M，Kiefer PW．The use of intensity hue－saturation transformations for merging Spot panchromatic and multi spectral image data［J］．Photogrammetric Engineering and Remote Sensing，1990，56:459－467．

［6］ Ehlers M．Multi sensor image fusion techniques in remote sensing［J］．ISPRS Journal of Photogrammetry and Remote Sensing，1991，46(1):19－30．

［7］ Shettigara V K．A generalized component substitution technique for spatial enhancement of multispectral images using a higher resolution data set［J］．Photogrammetric Engineering and Remote Sensing，1992，58(5):561－567．

［8］ Garguet－Duport B，Girel J，Chasseny JM，et al．The use of multire solution analysis and wavelets transform for merging SPOT panchromatic and multi spectral image data［J］．Photogrammetric Engineering and Remote Sensing，1996，62(9):1057－1066．

［9］ Zhou J，Civco D L，Silander J A．A wavelet transform method to merge Landsat TM and SPOT panchromatic data［J］．International Journal of Remote Sensing，1998，19(4):743－757．

［10］ 宋 杨，万幼川．一种自适应的基于局部小波系数特征的遥感图像融合方法［J］．遥感信息，2007(1):3－6．Song Y，Wan Y C．Remote sensing image fusion method based on adaptive local wavelet coefficients［J］．Remote Sensing Information，2007(1):3－6．

［11］ Kim Y，Lee C，Han D，et al．Improved additive－wavelet image fusion［J］．IEEE Geoscience and Remote Sensing Letters，2010，8(2):263－267．

［12］ 蔡 娜．基于小波变换的遥感图像融合方法研究［D］．福州:福建师范大学，2008．Cai N．Study of Fusion Method for Remote Sensing Image Based on the Wavelet Transform［D］．Fuzhou:Fujian Normal University，2008．

［13］ 范文婷，傅 平．一种基于小波变换的遥感图像融合方法［J］．国土资源遥感，2008，20(3):24－26．doi:10．6046/gtzyyg．2008．03．06．Fan W T，Fu P．A remote sensing image fusion method based on wavelet transform［J］．Remote Sensing for Land and Resources，2008，20(3):24－26．doi:10．6046/gtzyyg．2008．03．06．

［14］ 于 浩，孙卫东，常 玲，等．基于双树复小波的CBERS－02B星遥感影像融合及评价［J］．国土资源遥感，2009，21(1):55－59．doi:10．6046/gtzyyg．2009．01．12．Yu H，Sun W D，Chang L，et al．Remote sensing image fusion and evaluation of CBERS－02B based on dual tree complex wavelet transformation［J］．Remote Sensing for Land and Resources，2009，21(1):55－59．doi:10．6046/gtzyyg．2009．01．12．

［15］ Do M N，Vetterli M．The Contourlet transform:An efficient directional multire solution image representation［J］．IEEE Transactions on Image Processing，2005，14(12):2091－2106．

［16］ Do M N，Vetterli M．Framing pyramids［J］．IEEE Transactions on signal Processing，2003，51(9):2329－2342．

［17］ 王相海，魏婷婷，周志光．Contourlet方向区域相关性的遥感图像融合［J］．遥感学报，2010，14(5):905－916．Wang X H，Wei T T，Zhou Z G．Remote sensing image fusion method based on the contourlet coefficients’correlativity of directional region［J］．Journal of Remote Sensing，2010，14(5):905－916．

［18］ 吴一全，陈 飒．Contourlet变换和Tsallis熵的多源遥感图像匹配［J］．遥感学报，2010，14(5):893－904．Wu Y Q，Chen S．Multi－source remote sensing image matching based on Contourlet transform and Tsallis entropy［J］．Journal of Remote Sensing，2010，14(5):893－904．

［19］ 朱 康，贺新光．基于形态学和Contourlet系数区域特征的遥感图像融合方法［J］．计算机科学，2013，40(4):301－305．Zhu K，He X G．Remote sensing images fusion method based on morphology and regional feature of Contourlet coefficients［J］．Computer Science，2013，40(4):301－305．

［20］ Mahyari A G，Yazdi M．Panchromatic and multi spectral image fusion based on maximization of both spectral and spatial similarities［J］．IEEE Transactions on Geoscience and Remote Sensing，2011，49(6):1976－1985．

［21］ Cunha A L，Zhou JP，Do M N．Nonsub sampled Contourilet transform:Filter design and applications in denoising［C］//Proceeding of International Conference on Image Processing．Genova:IEEE，2005:749－752．

［22］ Zhou JP，Cunha A L，Do M N．Nonsub sampled Contourlet transform:Construction and application in enhancement［C］//Proceeding of IEEE International Conference on Image Processing．Genova:IEEE，2005:469－472．

［23］ Cunha A L，Zhou J P，Do M N．The Nonsub sampled Contourlet transform:Theory，design，and applications［J］．IEEE Transaction on Image Processing，2006，15(10):3089－3101．

［24］ Kong W，Lei Y，Ni X．Fusion technique for grey－scale visible light and infrared images based on non－sub sampled Contourlet transform and intensity－hue－saturation transform［J］．IET Signal Processing，2011，5(1):75－80．

［25］ Mallat SG．A theory for multire solution signal decomposition:The wavelet representation［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(7):674－693．

［26］ Wang Z，Bovik A C，Sheikh H R，et al．Image quality assessment:from error visibility to structural similarity［J］．IEEE Transactions on Image Processing，2004，13(4):600－612．