低压配电系统选择性保护短路电流峰值早期预测的算法研究
陈志英,陈丽安,缪希仁,赵 晶
(1.厦门理工学院电气工程与自动化学院,福建厦门 361024;2.福州大学电气工程与自动化学院,福建福州 350116)
0 引言
短路故障是低压配电系统常见故障之一,给供电系统及用户带来极大的危害.智能电网最主要目标就是要保证供电的可靠性与连续性.文[1-2]提出对低压配电系统而言,实现这一目标的重要手段是采用选择性保护,利用前后级断路器三段式保护的合理配合可实现局部选择性保护,对断路器结构改造如引入限流辅助回路、双断点后,可实现全局选择性保护.由于断路器采用三段式保护,实现系统短路保护需要一定时间,常常是几个周波,未能实现短路故障早期判断,使前级和正常支路设备也遭受一定时间的短路电流冲击,且由于选择性保护是依靠前一级断路器的短延时来实现,当配电系统层次较多时,难以实现系统的全局选择性保护功能,限制配电系统层次的扩大.文[3-4]提出采用先进传感及数据采集技术对低压配电系统电参数实时在线检测,利用现代数学手段对短路故障实现早期诊断,使故障处于萌芽状态时便判断出来并触发保护装置动作,从而减轻短路电流对电力系统及电气设备的威胁与破坏.本文结合文[1-2]观点,在文[3-4]实现短路故障早期诊断的基础上,提出一种低压配电系统选择性保护短路电流峰值早期预测计算方法.在诊断出系统短路后,该方法基于已采集的少量短路电流数据,采用最小二乘法进行曲线拟合,可预测出短路电流峰值,再根据峰值大小决定断路器是否动作,从而实现低压配电系统短路故障的早期全局选择性保护.
1 短路电流峰值早期预测算法
1.1 算法原理
低压配电短路故障可等效为一阶感性电路,如图1所示,U(t)为线路电源,I为线路电流,R为线路电阻,L为线路电感,LOAD为线路感性负载.
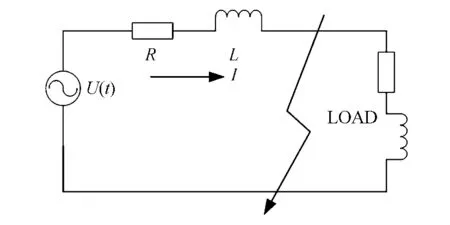
图1 低压短路故障等效电路Fig.1 Equivalent circuit of low - voltage shortcircuit fault
线路短路后,其电源侧电路参数变化性质用一阶微分方程表示为:
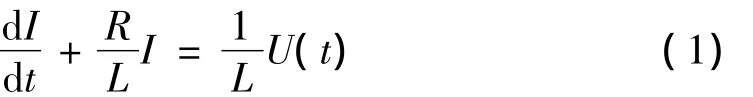
其中:U(t)=Umsin(ωt+φ),Um为电源电压幅值,ω为角频率,φ为短路发生时电源电压初相角.
借鉴灰色理论求解微分方程方法,将式(1)写为灰色理论白化方程[5]:

其中:x(1)为短路电流值(连续);a为线路时间常数倒数,a、b都为待求微分方程常系数,由R、L、Um确定.再将白化方程离散为:
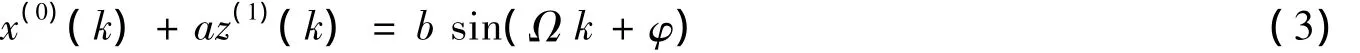
其中:Ω=2π/N称为数字角频率,N是一个周期内总的采样点数;k是采样点序号(k≥0);x(0)(k)称为已知采样点x(1)(k)的一阶累减AGO序列;z(1)(k)称为已知采样点x(1)(k)的MEAN紧邻均值生成序列.x(0)(k)、z(1)(k)计算表达式如下[5]:

由微分方程离散式(3),若已知k点短路电流数据x(1)(k)及短路发生时电压初相角φ,就可依据最小二乘法求出系数a、b,进而求出微分方程离散解.即短路电流预测序列表达式,从而求出短路电流峰值.下面推导a、b及短路电流预测序列表达式.
考虑一般性,从短路时刻(第0个点)起t0时刻(第N0点)开始取k点电流样本[6],则从第N0点开始的连续k点短路电流类原始数据序列为:

根据公式(3)~(5),得:
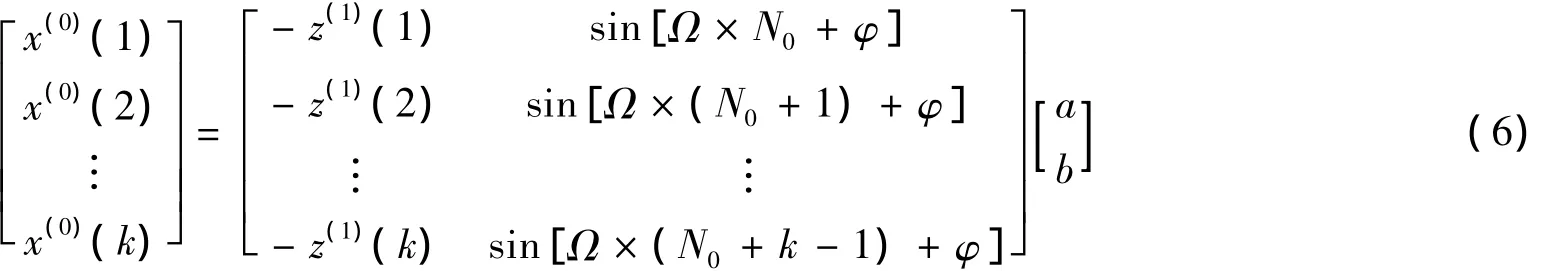
令

根据最小二乘法,得:

求出a、b后,由微分方程(2)及初始条件t0=N0Ts(Ts为电流采样周期)时x(1)=x(1)(1),得到微分方程连续解.将连续解离散化,求得短路时刻(t=0)之后电流信号x(1)的预测序列^x(1)(k)表达式为:
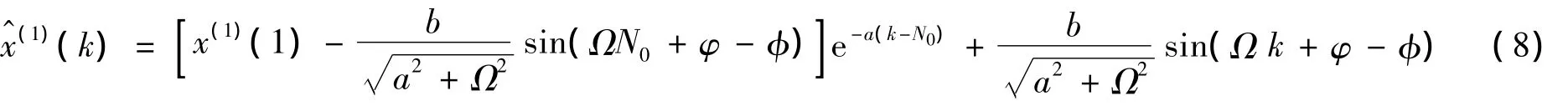
1.2 电压初相角与电流检测
由1.1分析可知,要实现短路电流峰值早期预测,必须在线路发生短路故障基础上已知少量短路电流数据及发生短路时电源电压初相角.因此,系统实时在线采样线路电流和电压过零点,利用光耦合器件检测到电压U(t)过零点后,开启定时器计时并同时开启A/D转换器采样电流I(t),采样频率50 kHz,每t0时间采集一组电流数据(一组40个数据,则t0=0.8 ms),并对数据进行形态小波变换计算诊断线路发生短路与否,若诊断结果为否定,则继续下一组电流采样与计算,直到诊断结果为肯定或下一个过零点重新开始.如图2所示,短路故障发生在td时刻,短路电流为Id(t),系统在电压过零点零时刻开始采样电流,经计算前n组数据(nt0前采样)短路故障诊断结果均为否定,当采样到nt0~(n+1)t0时间内电流数据,经计算短路故障诊断结果为肯定后,结束电流采样,关闭定时器.由于利用形态小波计算不仅能准确诊断出线路是否发生短路故障,且能准确诊断出发生故障处样本点序号[7],再结合定时器计时时间,就能推算出发生短路故障时间点为td,电源电压初相角为φ=ωtd.
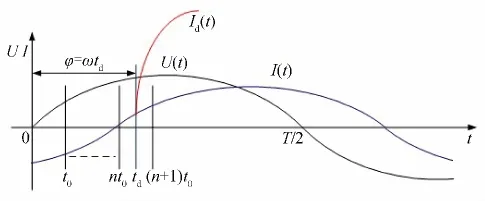
图2 电流与电压初相角信号采集示意图Fig.2 Sampling of current and initial phase of voltage
1.3 峰值预测
通过对线路电流实时监测,获得短路电流数学表达式后,峰值预测计算主要有两种方法:①求极值法,即将电流I(t)对时间t求导,找到极值对应时间点后代入电流表达式算出峰值,该方法用时短,实时性很高;②根据电流表达式按步进依次算出电流值,比较后求出最大值,该方法比较简单,但计算的数据量较多,耗时较长,比方法①逊色.本文重点介绍方法①.
由于短路发生时刻(t=0)电流比稳态时短路电流幅值小得多,因此,短路电流x(1)(t)可近似为:


通常线路呈感性,等效电感L比等效电阻R大的多,因此线路时间常数倒数a很小,上式第二项约等于0,因此可推得:cos(ωt+φ-φ)=0,即ωt+φ-φ =+nπ(n=0,1,2,3,…)时,短路电流有极值.将ω =,t=kT代入,求得电流极值点序号k:s

考虑到短路电流的暂态分量呈指数衰减,短路电流最大值将出现在第一个或第二个极值点,因此取n=0或n=1,得到短路电流峰值点序号:
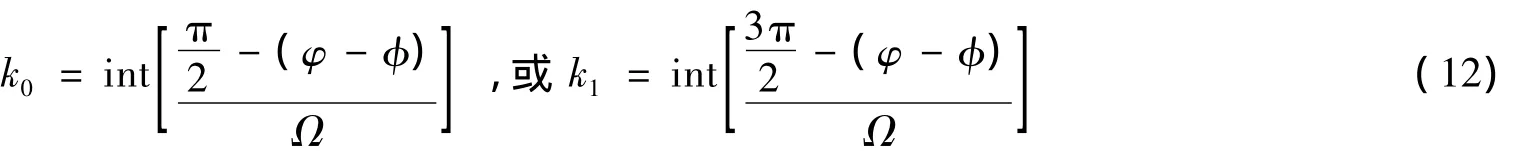
再将k0、k1代入短路电流预测表达式(8),值更大的电流为短路电流峰值.
2 短路电流峰值早期预测软件实现
短路电流峰值预测目的是通过少量已采集的电流数据推测出未来短路电流曲线的走势,从而得到短路电流的峰值.根据节1.1算法原理,取5个原始短路电流值x(1)(k)就能确定系数a、b,进而得到微分方程解,预测出短路电流峰值.确定系数a、b本质上也是曲线拟合的过程,为获得最佳拟合效果,本文采用下面方法实现短路电流峰值预测,方法原理如图3所示.
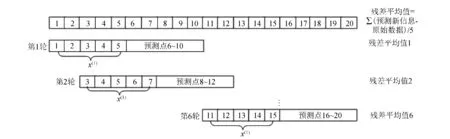
图3 软件实现方法原理示意图Fig.3 Diagram of software realization principle
原始短路电流数据的采样频率为50 kHz,每一组共40个原始数据(800μs内采集到的),间隔取点,获得20个原始短路电流计算数据.对已知20个电流数据分多轮次取5点作为x(1)(k),轮步进为2,利用最小二乘法计算出微分方程系数a、b,预测下5个点电流值,与原始值相减,得到残差(误差)平均值.若残差平均值小于给定残差平均值(预测精度高于预测要求),就认定该轮次的模型参数精度达到要求,曲线拟合很贴近真实曲线,无需进行下轮次计算;若残差平均值大于给定残差平均值,继续下一轮次取点并计算a、b.如此,最多计算6个轮次,倘若6轮次的残差平均值均大于给定残差平均值,则选取残差平均值最小轮次a、b作为最终系数.
C语言编程中,origin_x(1)(k)表示原始采集短路电流数据;def表示残差;avr表示残差平均值;n表示轮次;j表示步进值;i,k表示序号.程序设计流程如图4所示.取5点原始电流数据计算预测值与残差平均值,若残差平均值小于等于给定值,则认定为满足预测精度要求,确定预测模型,计算出短路电流峰值;若残差平均值大于给定值,则继续取点进入下一轮计算.

图4 短路电流峰值预测程序流程图Fig.4 Program flowchart of peak value prediction of short-circuit fault current
3 短路电流峰值预测结果
利用Matlab Simulink[8-11]对低压配电系统短路建模仿真获得短路电流数据,将电压初相角每间隔15°的短路电流数据输入到短路电流峰值预测程序中计算,得到短路电流预测峰值,再将预测峰值减去实际峰值得到误差值与相对误差.表1是预测短路电流峰值结果.可以看出,预测相对误差最小可达0.286%,最大只有3.625%,相对误差平均值为1.874%,预测精度很高,证明短路电流峰值预测的有效性.

表1 短路电流峰值早期预测结果Tab.1 Prediction result of short-circuit current peak value
因短路电流峰值预测算法包含乘加、三角和指数运算,所以选取TI公司32位浮点DSP芯片TMS320F28335对算法运行速度进行测试,该芯片时钟频率高达150 MHz,指令时钟周期为6.67 ns.测试结果如表2所示,各种电压初相角下算法运行时间均在1 ms之内,最大达0.788 ms,最小只需0.114 ms,可见算法执行速度快,实时性高,容易在硬件系统上实现.

表2 预测算法运行时间Tab.2 Run time of prediction algorithm
4 短路电流峰值实现全局选择性保护
如图5所示,QF1、QF2分别为低压配电系统前后级断路器安装位置,传统断路器是利用QF1三段式保护中的短延时实现选择性.但是QF1与QF2工作一段时间后,整定值可能出现漂移,导致QF1与QF2的特性配合不够准确,或是短路电流过大使得QF1由短延时阶段直接过渡到短路阶段,在支路3短路发生时QF1将越级跳闸,选择性保护失败.与利用断路器的特性实现选择性不同,本文利用监测电力线路实际短路电流实现早期全局选择性保护.QF1、QF2采用智能断路器,均实时检测线路电流,当支路3发生短路时,下级断路器QF2早期诊断出短路故障后动作,上级断路器QF1也诊断出短路故障,但因短路电流预测峰值未达到开断电流Icw则不动作,从而保证支路1、2正常供电,实现线路全局选择性保护.智能断路器还可将短路电流峰值发送到监控主机,由主机选择断路器动作.由于这种选择性取决于线路短路电流本身,因此它比传统的选择性保护更加准确可靠.

图5 前后级断路器安装位置Fig.5 Installed position of breakers
5 结语
在实现低压配电系统短路故障早期诊断基础上,结合最小二乘曲线拟合法,提出一种短路电流峰值预测计算方法.利用少量已采集电流数据与短路时电压初相角可准确预测出线路短路电流的发展趋势及峰值,大量仿真数据结果证明预测曲线非常贴近于真实的短路故障电流曲线,具有预测精度高,数据处理量少,运算量小,程序运行速度快等优势,有利于在硬件系统上的实时实现.短路故障早期诊断可以大幅度减轻短路对线路及设备的危害,利用峰值预测实现低压配电系统前后级断路器早期全局选择性保护后,进一步保证了线路供电的安全性与连续性.因此,本文提出的理论方法与实现方法具有一定的理论意义与实用价值,使智能断路器在早期短路故障检测的基础上实现早期全局选择性保护成为可能.
[1]陈德桂.智能电网与低压电器智能化的发展[J].低压电器,2010(5):1-6.
[2]陈德桂.选择型低压断路器的发展动态[J].电气技术,2009(6):16-18.
[3]陈丽安,张培铭.基于形态小波的低压系统短路故障早期检测[J].中国电机工程学报,2005(10):24-28.
[4]陈丽安,张培铭,缪希仁.基于小波变换的低压系统短路故障的早期预测[J].电工技术学报,2003(2):91-94.
[5]邓聚龙.灰预测与灰决策[M].武汉:华中科技大学出版社,2002.
[6]张大海,江世芳,史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践,2002(8):140-142.
[7]陈丽安,张培铭.形态小波在低压系统短路故障早期检测中的DSP实现[J].电工电能新技术,2005(1):31-34.
[8]于群,曹娜.Matlab/Simulink电力系统建模与仿真[M].北京:机械工业出版社,2011.
[9]王进超,缪希仁.低压配电系统单相短路故障的建模与仿真[J].低压电器,2012(22):15-18.
[10]包能胜,朱瑞丹,倪维斗.双馈型机组风电场三相电网短路故障暂态特性分析[J].控制理论与应用,2008(1):141-144.
[11]包能胜,朱瑞丹,倪维斗.大型风电场电网三相短路故障暂态分析[J].太阳能学报,2008(9):1 161-1 166.

