考虑偏好序且权重未知的群双边匹配决策

林 杨，王应明

(1．福州大学经济与管理学院，福建福州350116;2．福建师范大学经济学院，福建福州350117)

0 引言

双方互为决策的匹配问题，即双边匹配(bilateral matching)是决策科学的重要研究内容．其理论和方法在经济管理领域有广泛的应用背景，如电子商务背景下的供需双方匹配问题［1］，风险投资基金与创业公司的选择问题［2］，高校招生与学生升学的双向选择问题［3］，男女双方婚姻匹配问题［4］等．

双边匹配是指在两个不相交的主体集合中，各方主体根据已有的信息对潜在的匹配方给出偏好判断，并依此进行匹配．合理满意的匹配方案是管理实践追寻的目标．在双边匹配决策中，通常需要考虑双方的偏好序信息．有关这方面的研究，多年来得到国内外学者的广泛关注．Gale和 Shapley［5］最早研究了男女婚配问题并提出稳定匹配的概念，给出经典的G－S匹配算法．随后，Roth［6］和Balinski［7］等对G－S匹配算法进行全面讨论，提出一般意义下双边匹配的概念并证明双方均具有严格偏好时，存在Pareto最优的匹配方案;Abdulkadiroglu等［8］研究了弱偏好条件下的双边匹配及其特性，提出有效适应延期接受机制．Irving和Manlove［9］针对美国医学院毕业生与实习医院存在的现实问题，研究了不完全和不严格偏好序的匹配方法．樊治平、乐琦等［10－12］研究考虑完全偏好序以及稳定匹配条件的双边满意匹配，并建立优化模型求解最优匹配结果．梁海明等［13］针对主体给出弱偏好序形式的偏好信息的双边匹配问题，使用变步长算法求解优化模型．陈圣群等［14］针对高校课程与教学人员的匹配问题，使用证据推理求出双方的匹配度并构建优化模型．万树平等［15］针对风险投资商与企业匹配问题，考虑决策主体的风险规避的心理特征，基于前景理论和TODIM量化双方的匹配感知价值，并构建了评价指标为不同类型信息的匹配模型．以往研究为解决基于偏好序的双边匹配决策问题打下良好的理论基础．

需要指出的是，已有的研究都是局限于匹配主体在单人环境下进行决策．现实中，随着管理实践活动的日趋复杂，及力图避免个人认知偏差造成的决策失误，决策往往由多名人员共同参与［16］．例如在金融投资领域，面对众多的申请项目，投资公司必须拥有十分出众的智囊团对项目进行专业的甄别、调查论证及评价．遗憾的是，迄今鲜有对决策主体是多名成员，即群双边匹配进行深入研究．因此，群双边匹配是决策分析理论亟待解决的实际问题之一．鉴于此，本研究从双边匹配和群决策理论的综合视角，提出一种基于偏好序信息且权重未知的群双边匹配的决策方法．先由双方主体的每位群成员给出对另一方的偏好序信息和对匹配的乐观程度指数．再将偏好序转化为满意度，由乐观程度指数演算可得到群成员权重，并用OWA算子对个人满意度进行集结，生成主体群的综合满意度，并以双边主体群满意度最大为目标，建立单目标优化模型．最后，求解模型获得匹配方案．

1 相关概念

1．1 群双边匹配

群双边匹配可视为在双边匹配决策理论的基础上进行拓展延伸．匹配主体由单人增至多人，下面给出群双边匹配的定义．存在参与匹配的甲乙双方，甲方主体群为A={A1，A2，…，Am}，乙方主体群为B={B1，B2，…，Bn}(m，n≥2);不失一般性，令m≥n．其中:Ai表示甲方第i个主体群，Ai=(a1i，a2i，…，aipi)，=pi(pi≥2)，aik表示主体Ai中第k个成员，Bj表示乙方第j个主体群，Bj=(b1j，b2j，…，bjqj)，=qj(qj≥2)，bjl为主体Bj的第l个成员．

定义1 群双边匹配定义为映射μ:A∪B→A∪B，∀Ai∈A，∀Bj∈B，满足如下:① μ(Ai)∈B∪{Ai};② μ(Bj)∈A;③ μ(Ai)=Bj，当且仅当μ(Bj)=Ai，则称μ为群双边匹配．

定义2 若 μ(Ai)=Bj，则 μ(Bj)=Ai，称(Ai，Bj)是μ确定的一个主体群匹配对．若μ(Ai)=Ai，则称Ai在μ中未匹配．由μ确定的所有主体群匹配对的集合称为一个匹配方案．

1．2 偏好序与OWA算子

双边匹配是主体互相决策、择优选择潜在对象的过程．考虑双方给出偏好序形式的匹配信息．设Gi={g1i，g2i，…，gin}(i=1，2，…，m)为Ai给出的关于B的偏好序信息，其中:gik=(φ1ij，φ2ij，…，φipji)(j=1，2，…，n)，φikj表示 Ai第 k个成员 aik把 Bj排在第 φikj位．同理，Hj={h1j，h2j，…，hjm}，(j=1，2，…，n)为Bj给出的关于A的偏好序信息，其中:hjl=(φ1ji，φ2ji，…，φjpii)(i=1，2，…，m)，φjli表示Bj第l个成员 bjl把Ai排在第 φjli位．例如，φ233=1表示A2第3个成员a23把B3排在第1位．h21=(3，2，1，4)，表示B2共有4位成员，依次把A1排在第3，2，1，4位．

如上所述，群双边匹配的主体是由若干名成员组成，各成员关于潜在方的偏好可能不同．根据群决策理论，为确定最优匹配方案，必须将成员的个人偏好转化、集结为一种可以表示主体群作为独立单位的匹配信息．本研究使用OWA算子进行集结．OWA算子由美国著名学者Yager［17］提出，是一种介于最大与最小算子间的信息集结算子，为不同的决策准则提供了统一框架，定义如下:

定义3 设fw:Rn→R，W=(w1，w2，…，wn)T是与fw有关的加权向量，满足wj=1(0 ≤wj≤1，j=1，2，…，n)，若fw(a1，a2，…an)= wibi，其中bi是a1，a2，…an中第i个最大的数，则称fw是n维OWA算子．

1．3 综合满意度及满意匹配

为便于后续优化模型的建立，将给定的偏好序转化为满意度信息．

定义4 Ai成员aik对Bj的满意度为αikj，Bj成员bjl对Ai的满意度为βjli，记αikj=Sα(φikj)，βjli=Sβ(φjli);其中，Sα(·)，Sβ(·)是单调递减的非线性函数，均满足 S(·)≥0且 S(·)=1．根据文献［10］，Sα(·)和Sβ(·)可取:

其中:i=1，2，…，m;j=1，2，…，n;k≤ pi;l≤ qj．

定义5［18］群双边匹配 μ，∃Ai1，Ai2，Bj1，Bj2，i1≠ i2，j1≠ j2，其中 μ(Ai1)= μ(Bj1)，μ(Ai2)=μ(Bj2);若αi1j2+αi2j1≤αi1j1+αi2j2，βi1j2+βi2j1≤βi1j1+βi2j2且等式不同时成立，则μ是不满意匹配，否则是满意匹配．

本文要解决的问题是，考虑匹配双方的主体群各成员给出的偏好序信息且成员权重未知，运用何种决策方法，确定最优满意匹配方案．

2 群双边匹配方法

2．1 计算主体的综合满意度

得到主体群成员的个人满意度后，需对其进行集结并生成主体群的综合满意度．集结是联合个体的不同建议、评价并产生关于群的量值［19］．在群决策理论中，信息集结一般会涉及成员的权重．受环境、知识、经验等因素的局限，一般群成员不易直接给出准确的权重，而权重影响最终匹配方案的满意度和可靠性．因此，如何合理、有效地确定群成员权重是群双边匹配的一个关键环节．

根据行为理论［20］相关研究，在决策过程中，主体自身的乐观程度测度相对容易假定．针对匹配中群成员权重未知的特点，使用笔者提出的基于OWA算子的极大极小离差法［21－22］，一种给定ORNESS测度下，通过最小化任意两个相邻成员之间的权重差值求得一组最优权重．在双边匹配中，ORNESS测度可看成主体群对当前匹配的乐观程度倾向．因此，当已知主体群对匹配方的乐观程度倾向，运用极大极小离差法就得到群成员基于OWA算子的权重，过程如下:

设 Ai，Bj给出的 ORNESS值分别为εi，λj∈［0，1］，aik，bjl的权重分别是ωik，ωjl，根据极大极小离差法，ωik，ωjl可由式(3a)，(3b)确定:

从式(3)可知，ORNESS值越接近于1/0，主体群对当前匹配越倾向于乐观∕悲观．ORNESS=0．5表示主体持中立态度，且每位成员的权重均为1 pi．

例1 主体群Ai由5位决策者组成，经协商给出的ORNESS值ε=0．7．则依据式(3)，基于OWA算子的群成员权重(ωik)k=(0．36，0．28，0．20，0．12，0．04)(k=1，2，…，5)．

得到各组群成员的权重后，使用OWA算子进行集结．设已知aik对 Bj的满意度 αikj，bjl对Ai的满意度βjli，

k≤ pi，l≤qj，i=1，2，…，m，j=1，2，…，n;ωik，ωjl分别是αikj和βjli的权重，Ai对Bj的综合满意度αij，及Bj对Ai的综合满意度βji为:

2．2 优化模型的建立

得到双方主体群的综合满意度后，以最大化双方的综合满意度之和为目标，建立优化模型．设xij是0～1变量，若μ(Ai)=Bj，则xij=1，否则xij=0．建立优化模型(5):

式(5)中φk(k=1，2)为各方参与匹配的重要程度，满足0≤φ1，φ2≤1，φ1+φ2=1，可由专家或权威部门确定．一般而言，参与双方地位平等时，为体现公平合作，取φ1=φ2=0．5．c1ij(c2ij)为Ai(Bj)对Bj(Ai)的综合满意度，(5a)为决策目标，(5b)表示最大化双方综合满意度之和．(5c)、(5d)的含义是主体群Ai或与某一个主体群Bj匹配，或未匹配，主体群Bj至多与A方某一个主体群匹配．

2．3 模型的求解

该模型存在最优解［10］．模型(5)是0～1单目标整数规划模型．目标函数和约束条件均为线性的，可采用线性规划方法求解;当问题规模不大时(i，j≤50)，也可使用Lingo、Excel Solver对模型(5)进行建模求解．当问题规模较大，则不宜直接采用上述方法．近年来发展起来的智能优化算法适用于这种情况［23－24］．根据文献［23］的思路，经修改设计如下的可行解有界排序法，可用于求解当问题规模较大(50≤i，j≤500)时的情形．

设fy为目标函数，X={x1，x2，…，xn}为fy的可行解集，x*∈X是所求的最优解．根据文献［23］，存在线性有界函数fb(z)，fb(z)=φi(zi－z~)且fb(z)≤fy(z)，其中:z是向量评价函数，z=λixi，λi＞0且 λi=1;z~是随机选取的参考向量评价函数， φi=1，k=2．

算法:可行解有界排序法

① 选取fb(z)的一个初始可行解，记为x1，x*=x1，i←1;

②i=i+1;

③ 求fb的第i位最优解xi;

④如果fy(xi)＞fy(x*)，则 x*=xi，否则x*=x*i－1;

⑤重复步骤② ～④，直到fy(x*)＞=fb(xn);

⑥返回最优解x*．

综上所述，考虑偏好序信息且权重未知的群双边匹配方法步骤如下:

步骤1 根据式(1)和(2)，将双方主体群成员偏好序φikj、φjli分别转化为个人满意度αikj和 βjli;

步骤2 根据式(3)，由各主体群给定的ORNESS值，计算群成员的权重;

步骤3 由步骤1和2得到的个人满意度和权重，根据式(4)、(5)求出双方各主体群的综合满意度;

步骤4 依双方综合满意度，以最大化双方综合满意度之和为目标，建立0～1单目标优化模型(5);

步骤5 求解模型(5)，得到满意匹配方案．

3 算例

2014年6·18海交会上，有5家台资高新企业来闽，寻求有技术需求的陆资企业共拓闽台合作新优势．经初步了解磋商，有6家陆资企业表达了潜在的合作意向．为保证双方共同利益，需使配对成功的企业满意度最高．组委会决定每家企业的决策层先进行内部商讨，对潜在的合作方给出偏好信息．再集结成员的偏好信息作为企业的满意度评价．然后，组委会以双方满意度最大为目标撮成意向双方．5家台资企业记为集合T={T1，T2，…，T5}，6家陆资企业记为集合L={L1，L2，…，L6};台资企业Ti主要从企业规模、信用评级、技术能力建设和风险规避能力等指标评价陆资企业．陆资企业Lj重点考察台资企业的技术转让成本、技术转化风险、创新体制建设和信用评级等指标．此外，根据政策环境，交易成本等因素，双方给出对本轮闽台合作的乐观程度(ORNESS)值．组委会收到双方的偏好序信息和乐观程度指数如表1、2所示(第一列括号内为ORNESS值):

表1 台资企业给出关于陆资企业的偏好序(Ti)Tab．1 The preference ordinals provided by Taiwanese enterprises(Ti)

表2 陆资企业给出关于台资企业的偏好序(Lj)Tab．2 The preference ordinals provided by China Mainland’s enterprises(Lj)

根据式(3)，可求得双方主体群各成员权重，其中，5家台资企业的成员权重分别为:wT1=(0．433，0．333，0．233)，wT2=(0．333，0．333，0．333)，wT3=(0．8，0．2)，wT4=(0．43，0．31，0．19，0．07)，wT5=(0．25，0．25，0．25，0．25);

6 家陆资企业的成员权重依次为:wL1=(0．25，0．25，0．25，0．25)，wL2=(0．433，0．333，0．233)，wL3=(0．633，0．333，0．333)，wL4=(0．5，0．5)，wL5=(0．533，0．333，0．133)，wL6=(0．4，0．6);由式(1)、(2)转化得到的个人满意度见表3、4;在此基础上使用OWA算子进行集结，得到双方主体群的综合满意度，如表5、6所示．

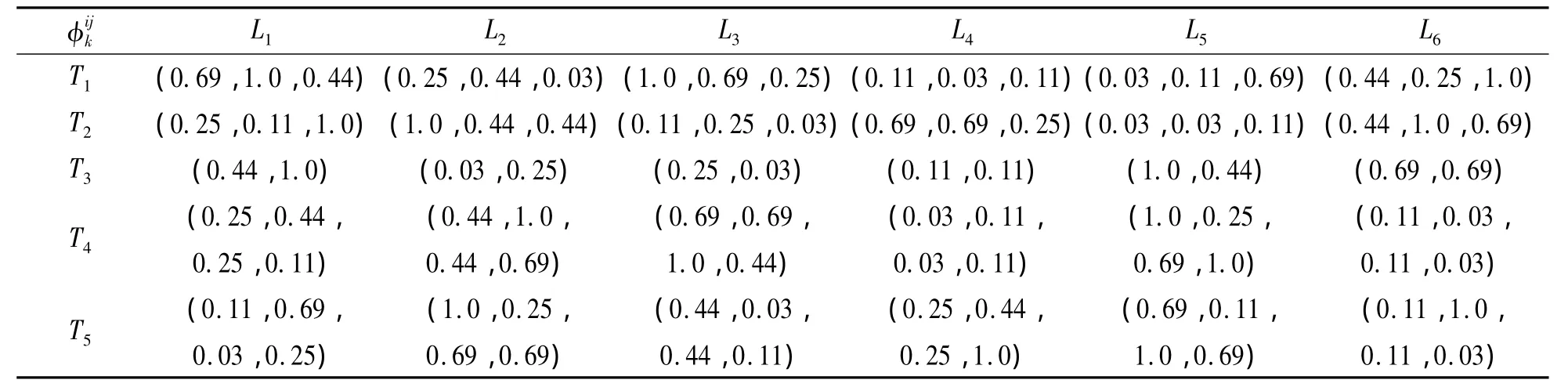
表3 转化后各台资企业的群成员个人满意度Tab．3 The satisfaction degree of each group member of Taiwanese enterprises

依据表5、6双方的综合满意度信息C1，C2，将其表示为矩阵形式并且C2转置，建立如下0～1单目标优化模型:

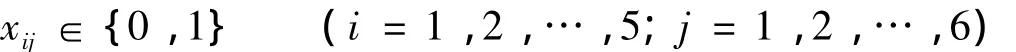
由于双方合作建立在平等互信基础上，组委会取φ1=φ2=0．5．使用Matlab软件包求解得δ=3．09，最优解X*为:

即匹配方案为:{(T1，L3)，(T2，L6)，(T3，L1)，(T4，L5)，(T5，L2)}．L4未匹配成功．下面对匹配方案进行验证．以匹配对(T1，L3)和(T2，L6)为例，根据定义5，α16+ α23=1．43，α13+ α26=0．77，β31+ β62=1．37，β32+ β61=1．04;即 α13+ α26≤ α16+ α23，β32+ β61≤ β31+ β62．类似的，对匹配方案中的匹配对两两验证，可知该匹配方案满足定义5．故该方案为满意匹配．

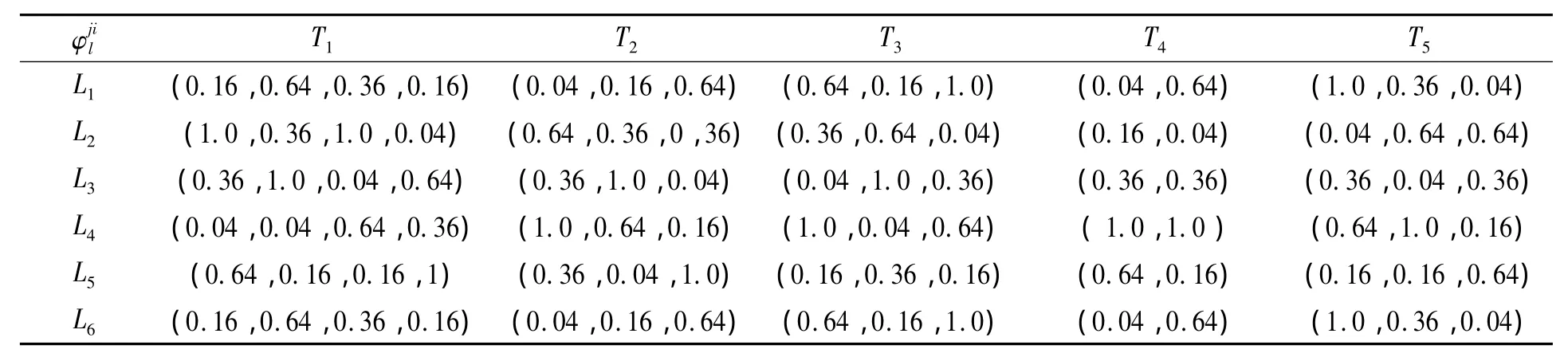
表4 转化后各陆资企业的群成员个人满意度Tab．4 The satisfaction degree of each group member of China Mainland’s enterprises

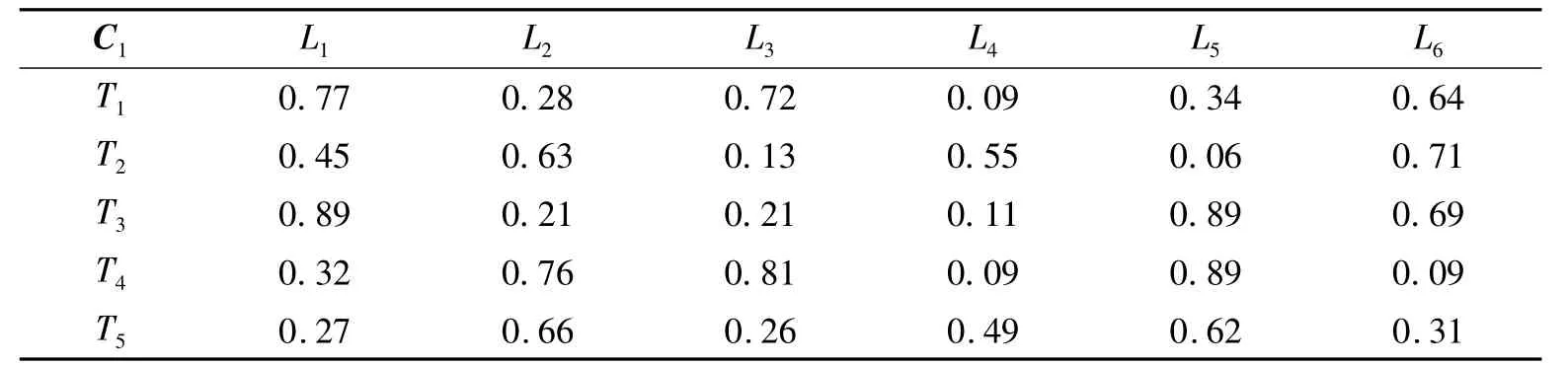
表5 台资企业对陆资企业的综合满意度Tab．5 The comprehensive satisfaction degree of Taiwanese enterprises

表6 陆资企业对台资企业的综合满意度Tab．6 The comprehensive satisfaction degree of China Mainland’s enterprise

4 结语

针对考虑偏好序信息且权重未知的群双边匹配问题，提出一种匹配决策方法．该方法结合双边匹配和群决策的理论方法．先由双方主体群的每个成员给出对另一方主体群的偏好序信息．再将偏好序转化为满意度，根据主体群给定的乐观程度指数，求出群成员基于OWA算子的权重，并生成主体群的综合满意度．以双方的主体群综合满意度最大为目标建立匹配决策模型，并进一步阐述当问题规模较大时，用可行解边界排序法进行求解，得到匹配方案．本文提出的群双边匹配方法，计算量适中，不仅丰富了双边匹配决策理论，而且有较强的应用背景，为管理活动中遇到的群双边匹配问题提供决策理论支持．

［1］Sarne D，Kraus S．Managing parallel inquiries in agents’two－ sided search［J］．Artificial Intelligence，2008，172(4/5):541－569．

［2］Elitzur R，Gavious A．A multi－period game theoretic model of venture capitalists and entrepreneurs［J］．European Journal of Operational Research，2003，144(2):440－453．

［3］Pais J．Random matching in the college admissions problem［J］．Economic Theory，2008，35(1):99 －116．

［4］Teo C P，Sethuraman J，Tan W P．Gale － Shapley stable marriage problem revisited strategic issues and applications［J］．Management Science，2001，47(9):1 252．

［5］Gale D，Shapley L．College admissions and the stability of marriage［J］．American Mathematical Monthly，1962，69(1):9 －15．

［6］Roth A E．Common and conflicting interests in two－sided matching markets［J］．Economic Review，1985，27(1):75－96．

［7］Balinski M，Snmez T．A tale of two mechanisms:student placement［J］．Journal of Economic Theory，1999，84(1):73 －94．

［8］Abdulkadiroglu A，Pathak PA，Roth A E．Strategy－proofness versus efficiency in matching with indifferences:redesigning the New York City high school match［R］．New York:National Bureau of Economic Research，2009．

［9］Irving R W，Manlove D F，Scott S．The hospitals－residents problem with ties［J］．Lecture Notes in Computer Science，2000，1 851:259－271．

［10］樊治平，李铭洋，乐琦．考虑稳定匹配条件的双边满意匹配决策方法［J］．中国管理科学，2009，17(4):113－118．

［11］樊治平．基于完全偏好序信息的严格双边匹配方法［J］．管理科学学报，2014，17(1):21－34．

［12］Fan Z P，Yue Q，Bo F．An approach to group decision making with uncertain preference ordinals［J］．Computers＆ Industrial Engineering，2007，58(1):51－57．

［13］梁海明，姜艳萍．一种基于弱偏好序信息的双边匹配决策方法［J］．系统工程学报，2014，22(9):154－159．

［14］陈圣群．高校课程与教学人员的匹配决策方法［J］．福州大学学报:自然科学版，2013，41(6):986－989．

［15］万树平．具有不同类型信息的风险投资商与投资企业多指标双边匹配决策方法［J］．中国管理科学，2014，22(2):40－47．

［16］尤天慧，李洪燕，刘彩娜．一种具有不确定偏好序信息的多指标群决策方法［J］．中国管理科学，2013，21(5):110－114．

［17］Yager R．On ordered weighted averaging aggregation operators in multicriteria decision making［J］．IEEE Transactions on Systems，Man and Cybernetics，1988，18(1):183 －190．

［18］Vicki K．Marriage matching and gender satisfaction［J］．Social Choice Welfare，2009，32(1):15 －27．

［19］Wang Y M，Fan Z P．Fuzzy preference relations:aggregation and weight determination［J］．Computers＆ Industrial Engineering，2007，53(1):163－172．

［20］Gavetti G．PERSPECTIVE:toward a behavioral theory of strategy［J］．Organization Science，2012，23(1):267－285．

［21］Wang Yingming，Parkan C．A minimax disparity approach for obtaining OWA operator weights［J］．Information Sciences，2005，175(1/2):20－29．

［22］Wang Yingming，Parkan C．A preemptive goal programming method for aggregating OWA operator weights in group decision making［J］．Information Sciences，2007，177(8):1 867 －1 877．

［23］Lucie G，Patrice P，Olivier S．Choquet－ based optimisation in multi－objective shortest path and spanning tree problems［J］．European Journal of Operational Research，2010，204(2):303－315．

［24］蒋忠中，樊治平，汪定伟．电子中介中具有模糊信息且需求不可分的多属性商品交易匹配问题［J］．系统工程理论与实践，2011，31(12):2 355－2 366．