国际市场现货价格与期货价格指数波动的GARCH族分析

王 娟

（西安邮电大学 经济与管理学院，西安 710121）

0 引言

经济全球化背景下最大的特点就是国际、国内市场间的物资、技术、信息流变的更加频繁，不同经济体内部的风险通过国际贸易、外汇交易进行传导。在日益紧密的贸易联系下，国际市场上的大宗商品价格波动对中国国内的商品价格变动产生了极为巨大的影响，这种波动冲击将随着贸易依存度的增加变的更加显著。本文拟采用恩格尔提出的自回归条件异方差模型（ARCH）以及其他学者进行拓展得到的GARCH、TARCH、EARCH、对称与非对称的CARCH模型对国际现货与期货市场的“波动集聚性”、“杠杆效应”、收敛性进行分析。

在数据选择方面，考虑到金融市场所发挥的重要作用，同时选择国际现货与期货市场的商品价格指数，该两种指数均为国家发改委价格监测中心编制，被称为中价国际A指数（包含29种商品）和中价国际B指数（包含22种商品）。数据来源于“中国价格信息网”，研究时段为2005年6月至2014年6月。

1 现货与期货价格指数的ARCH效应检验与GARCH估计

1.1 ARCH效应检验

价格指数与金融序列同样具有一维随机游走特征，并且为了便于处理和消除数据波动带来的影响，本文对A、B指数同时求自然对数，即形成：

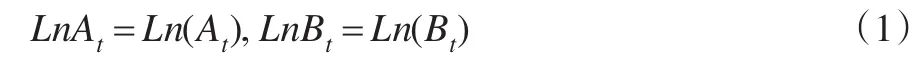
然后形成ARCH基本方程：

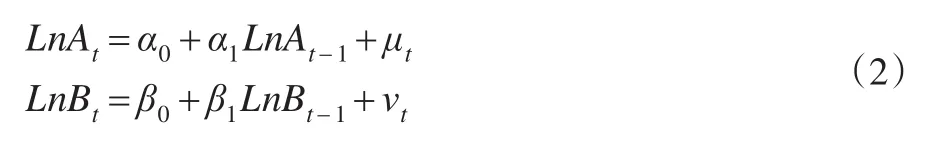
表1给出了国际市场现货与期货价格指数均值方程的估计结果，两个方程均显示常数项与滞后1阶的估计系数在5%水平显著异于0，且拟合系数分别为0.898和0.928，说明拟合程度良好，F统计量为939.14、1367.24，说明联合显著性高。估计后得到了方程随机误差项，通过三个工具来考察误差项的条件方差是否存在时变特征：一是观测误差项的波动走势，二是通过滞后残差平方的PAC、AC与Q统计量进行判定，三是构建辅助回归方程形成拉格朗日ARCH-LM统计量，进行综合判定。

表1 A、B指数的一维随机游走模型估计

判定1：在EVIEWS6.0方程估计窗口中分别生成残差序列ResidA和ResidB,并作图得到图1。图中横轴为观测时日的长短，纵轴为（2）估计误差，发现两个误差项波动具有协同性，走势较为一致，且随机误差项同时存在着“波动集聚性”，即波动具有惯性和跟随性，1～25期间和35～50两个区间内的波动幅度较大，而在75期以后的波动较低。

图1 误差项序列走势

判定2：在估计界面进行滞后残差平方的自相关与Q统计量检验，可以发现，对于ResidA其滞后残差1阶时自相关系数处于95%的置信区间之外，且Q统计量对应的P值很小，说明拒绝“不存在ARCH效应”的原假设；ResidA的滞后残差平方自相关系数在1、2期处于95%置信区间外，且各期的Q统计量非常显著，同样拒绝“不存在ARCH效应”的原假设。

判定3：以当期误差平方为被解释变量，误差平方滞后为解释变量，得到方程滞后残差平方的联合显著性系数F值与T*R^2的ARCH-LM统计量，检验方程中滞后阶数的选择应当越大越好，本文选择10。指数A的误差项F和LM统计量显示直到滞后10期不存在ARCH效应，指数B的误差项相应统计量在1%水平认为存在ARCH效应。

表2 A、B指数的拉格朗日乘数检验

1.2 GARCH（1,1）估计

根据上述检验，发现国际市场现货与期货市场指数整体上存在ARCH效应，即有时变方差和波动集聚性。在实践中，为了保持条件方差非负，方差方程中估计系数均大于0，故采用广义的GARCH模型进行估计。本文采用GARCH（1，1）模型，即条件方差受到其自身滞后1期和误差平方滞后1期限的影响。在估计之前需要进行数据转换，对指数A、B进行自然对数序列的一阶差分，即:

得到的RA，RB为收益率含义。构建均值方程的前提是滞后长度的选取，根据两个序列自相关系数图进行确定，RA的AC和PAC系数在所有长度上处于95%置信区间内，Q统计量不显著。RB的AC和PAC系数在1期超越了95%置信区间。故对两个序列的均值方程设置如下：

估计结果如表3。现货市场相应的均值方程和条件方差方程中大多数系数不显著，说明条件方差不受到滞后方差和误差平方滞后的影响，即不存在ARCH效应，这与“判定3”结论相符。期货市场对应的条件方差方程中GARCH和ARCH项估计系数至少5%检验水平显著，GARCH系数为-0.410，ARCH项系数为0.635，两者之和为0.225＜1，条件方差将会处于收敛状态。

图2给出了期货价格指数的GARCH模型估计后得到的残差序列、真实值和拟合值，发现真实值和拟合值走势几乎完全一致，而残差项几乎平行于0轴，故认为拟合情况良好。图3给出了条件方差的走势图，发现在40～45时段国际期货价格指数在这个时段波动较大，而在其他绝大部分时段，波动幅度较小。

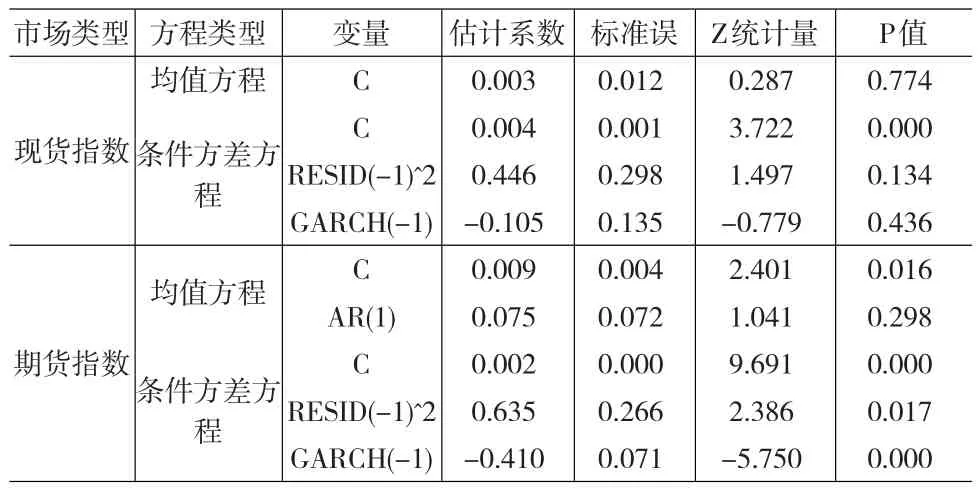
表3 GARCH（1,1）估计结果

图2 估计模型拟合值、实际值与残差

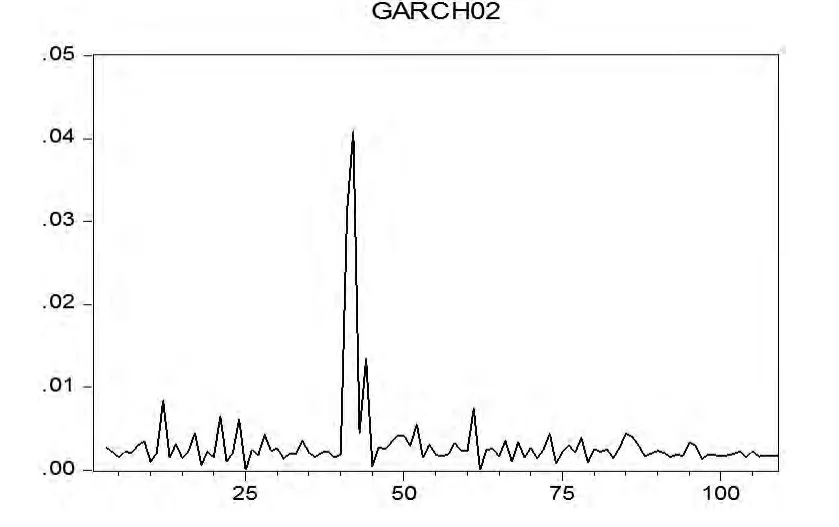
图3 估计模型的条件方差

2 期货价格指数的非对称性检验与方差均值的时变性检验

2.1 门限与指数ARCH估计

在金融领域，大量研究发现资产价格同等程度的下降相比上涨所带来的波动效应更为强烈。本文通过门限ARCH和指数ARCH进行估计，两个模型如下：

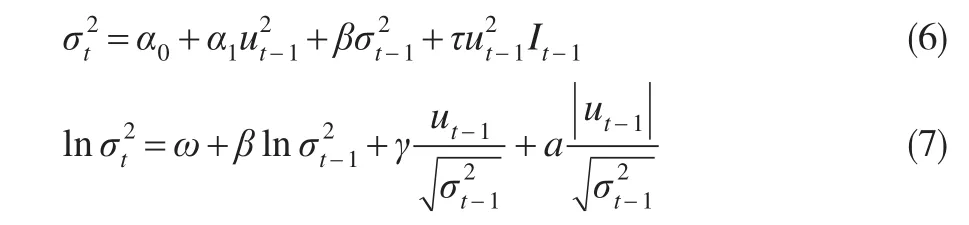
式(6)中It-1为非对称系数，如果ut-1＜0，则 It-1=1，反之为0。式（7）中γ为负意味着杠杆效应存在，反之不存在。式（7）中因为条件方差取对数，所以估计系数可以为负。估计结果如表4。TARCH估计结果中非对称系数τ的估计系数为0.1480，但t统计量对应的P值为0.5033，在10%检验水平不显著，说明期货市场价格波动不存在非对称效应。EARCH估计结果中非对称项γ的估计系数为负，但是对应的t统计量P值为0.1232＞0.1,同样认为“杠杆效应”不存在。

表4 非对称效应模型估计

2.2 方差均值时变检验—CARCH

GARCH、TARCH、EARCH模型都假定条件方差的均值不变，无法体现出长期波动与短期波动的关系，将使用成分ARCH模型进行估计，因为期货市场收益率序列呈现出“尖峰厚尾”特征，故采用学生t分布替代高斯分布进行估计。故表5最后1列给出了T-DIST.DOF系数，发现估计系数的T统计量为2.602，在1%检验水平显著。非对称性CARCH模型如下：

上式中第一个式子是长期成分公式，其取决于长期成分滞后值、随机误差项平方滞后与条件方差滞后间的差值，第二个方程是短期波动方程，取决于随机误差项滞后与长期成分滞后间的差值、条件方差滞后与长期成分滞后间的差值。表5中C(1)对应于ω.C(2)对应于 ρ，λ对应C(3)，α和β对应C(4)和C(5)。表5说明：长期波动率的均值为0.001，持续系数为0.997＜1,即长期波动率将缓慢收敛于均值0.001，短期波动率方程中α+β=0.320-0.594＜0,说明短期波动也会收敛于0。

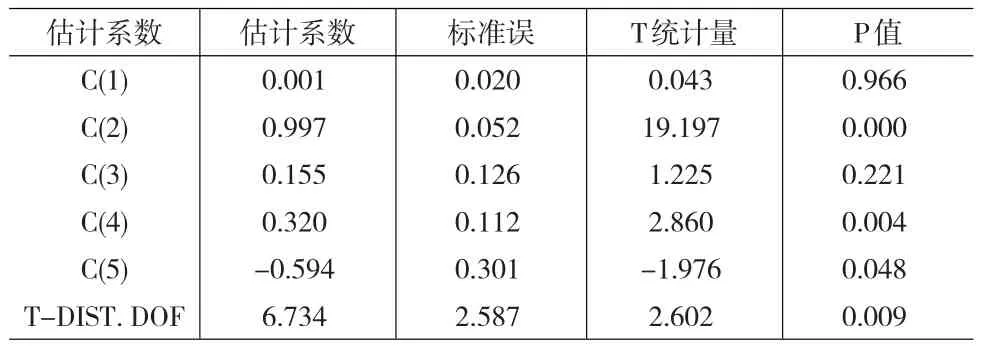
表5 对称CARCH模型估计结果

继续在CARCH中添加非对称项，该项只存在于短期波动方程中，即:

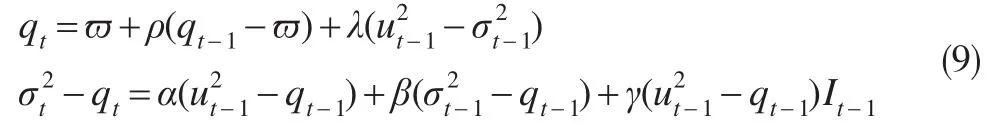
其中ut-1＜0，It-1=1，反之为0。长期波动率方程显示方差均值为0.0119，而持续系数为1.0019＞1,说明波动率均值不会收敛，而处于发散状态。短期波动方程中非对称项估计系数γ=0.2574，且对应z统计量的伴随概率为0.0787，在10%检验水平下显著，而随机误差项平方滞后期的估计系数为0.3303，说明在国际期货交易市场上，价格上涨消息所带来的冲击幅度为0.3303，而下跌消息带来的短期波动效应为0.3303+0.2574=0.5877，波动冲击将会带来一倍。上述结论与非对称的ARCH模型相悖，本文根据两个模型估计得到的AIC、SC、HIQC信息值进行判定，前者的对应值分别为-3.211、-3.062、-3.151，而后者为-3.230、-3.056、-3.160，后者的AIC和HIQC更小，总体判断非对称的ARCH估计效果较优。

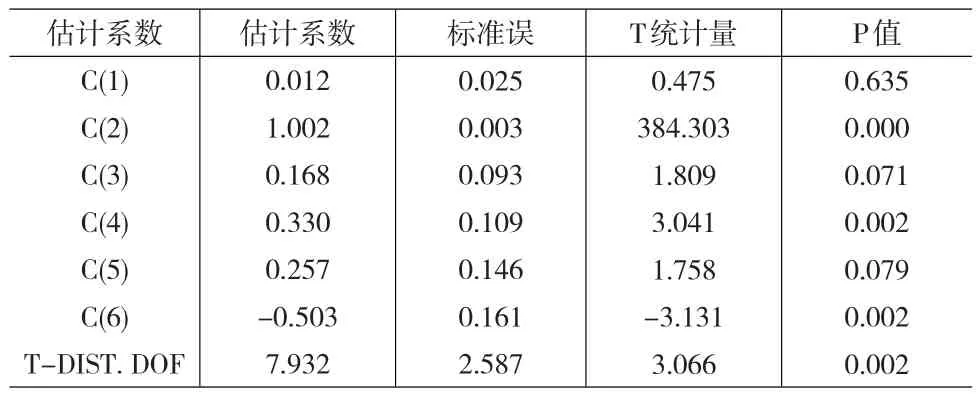
表6 非对称CARCH模型估计结果

3 结论

本文对国际市场现货与期货价格指数的波动特征进行了解析，结论如下：（1）国际现货市场价格指数没有呈现出“大波动跟大波动，小波动跟小波动”的时变方差特征，但一维随机游走模型的残差平方相关系数图显示期货市场价格指数的波动存在ARCH效应，即波动簇群性。（2）期货价格指数不存在显著的非对称性冲击，即等量好消息和坏消息带来的波动冲击效应是一致的，不存在“杠杆效应”，非对称的CARCH模型认为期货价格指数长期波动的均值处于发散状态，并且在短期波动中存在着显著的非对称项，即负面消息带来的短期波动较大。

上述结论说明，国际现货市场价格从波动角度看是无法进行预测的，但期货价格具有较强的集群效应，是可以运用GARCH模型进行预测的。在期货市场中，杠杆效应不明显，说明国际期货市场中的交易者整体上比较理性。本文的缺陷在于：一是没有对国际现货与期货市场之间、国际市场价格与国内市场价格之间的绝对冲击关系和相对波动溢出效应进行检验，二是从波动分析角度看，SV波动率模型可能更加有效，三是未能对未来国际市场价格进行精确预计，期待其他学者在本文基础上进一步展开相应研究。

[1]张勇.中国粮食市场与国际市场价格整合度研究——基于1997～2011年中美小麦和玉米价格的分析[J].湖南农业大学学报(社会科学版),2013,（4）.

[2]张巨勇，于秉圭，方天.我国农产品国内市场与国际市场价格整合研究[J].中国农村经济，1999,（9）.

[3]焦军普.国际市场价格上涨对我国国内价格影响的实证分析[J].经济与管理研究，2007,（9）.

[4]范志勇,向弟海.汇率和国际市场价格冲击对国内价格波动的影响[J].金融研究，2006,（2）.

[5]高铁梅.计量经济分析与建模[M].北京：清华大学出版社，2006.