基于概率排序模型的中国物流业发展趋势分析

罗玲桃，张相斌

(南京邮电大学 管理学院，南京 210023)

0 引言

物流业是融合运输业、仓储业、和信息业等行业的复合型服务产业，被广泛认为是继生产和营销之后的“第三利润源泉”。作为国民经济的重要组成部分，物流业正在全球范围内迅速发展，其发展水平已成为衡量一个国家综合竞争力的重要标志[1,2]。分析和预测我国现代物流业发展前景，有利于全面把握我国物流业发展动态，从而制定正确的物流业发展政策，科学规划物流系统，合理配置物流资源，达到进一步促进经济持续高效发展的效果。回归分析作为一种简单实用的预测工具，被广泛应用于各个领域的研究中[3～6]。目前，线性回归模型也是物流预测研究中运用较多的一种方法[5,6]。我们在利用回归模型进行预测时，一般是将单一的自变量预测值带入回归模型来预测因变量的未来水平，这种预测往往只反映出自变量单一的可能性。然而，随着人们对未来宏观环境的预期水平不同，自变量的预测值将呈现出多种可能性，仅仅依靠回归分析显然不足以描述自变量的这种波动水平。为了充分考虑自变量未来变化的不确定性和波动性，将自变量所有可能的预测值都纳入考虑范畴，本文在建立概率排序型预测模型的基础上，对中国物流业发展趋势进行预测。此前已有学者对概率排序型决策方法进行了一些研究[7～9]，但概率排序法在预测方面的研究较少，本文提出的概率排序型预测方法具有一定的创新性。概率排序型预测研究的是预测者对自然状态出现概率有所了解，但又不足以单值地计算出准确数值来的一类问题，概率排序型预测有效地弥补了研究中主观概率值缺失的缺陷。在概率排序型预测中，各自然状态的概率值未知，因而无法准确计算各期望值，但能够设法确定出期望值可能的最大值和最小值，预测结果以区间的形式描述，更加符合实际。

1 中国物流业发展趋势预测分析

1.1 指标的选取

物流业的发展水平受到需求和供给两方面的影响。物流需求拉动物流业蓬勃发展的同时，如果物流能力供给不能满足这种需求，物流能力供给将对物流发展产生抑制作用，将其限制在一定的发展水平；反之，当物流能力的供给水平很高，而物流需求不足以满足这种供给时，不可避免地会造成供给的浪费，物流业的发展水平受到需求的制约。因此，物流需求水平和供给水平共同决定了物流业的发展水平。物流是供需平衡的产物，这是物流最基本的特征。我们可从供需两方面入手确定影响物流业发展水平的关键影响因素及相应地指标。

影响物流业发展的关键影响因素是：社会经济水平、运输能力和仓储能力。其中，社会经济水平用GDP指标描述；运输能力不仅表现在运送的吨数上，还表现在货物被运送的距离上，所以采用全社会货物周转量表征；从统计上[10]看，储存主要存在于仓库和站场港口中，仓储业固定资产投资额从一定程度上反映了储存所需固定资产的建设情况，可以从侧面刻画仓储水平。

关于物流业发展水平，用于描述的指标有很多，如：社会物流需求系数、社会物流总额、物流总费用、物流业增加值、物流业增加值占同期GDP的比重等，其中，社会物流总额是业内常用的物流统计指标之一，本文用社会物流总额来衡量物流业发展水平。

1.2 物流业发展水平回归预测模型及局限

根据1991～2013年的相关统计数据（表1），采用回归分析法建立社会物流总额与GDP、全社会货物周转量和仓储业固定资产投资额之间的回归预测模型。

由于上文中关键影响因素主要是参照现有文献并加入自己的思考后总结而来，具有一定的主观性，为了加强本文的科学性和严谨性，在得到相关统计数据后，可绘制相关图来检验关键影响因素的选取是否合理。

图1 社会物流总额与GDP散点图

图2 社会物流总额与货物周转量散点图

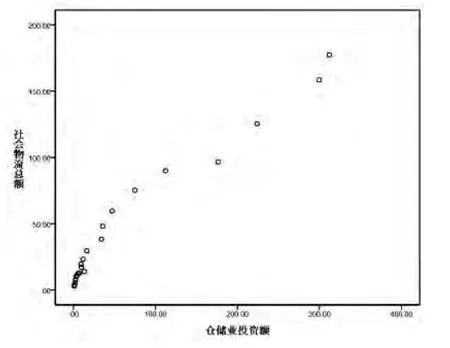
图3 社会物流总额与仓储业投资额散点图

观察图1～3可知，社会物流总额与GDP、货物周转量和仓储业投资额之间存在线性关系，关键影响因素选取合理。基于以上分析，假设社会物流总额关于GDP、全社会货物周转量和仓储业固定资产投资额呈多元线性回归。则社会物流总额模型为：

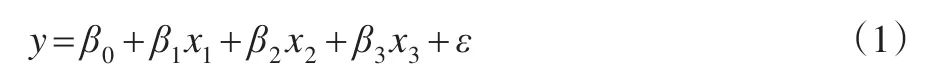
其中：y表示社会物流总额（万亿元）；x1表示GDP（万亿元）；x2表示货物周转量（万亿吨公里）；x3表示仓储业投资额（十亿元）；β0，β1，β2，β3表示参数；ε表示随机误差。

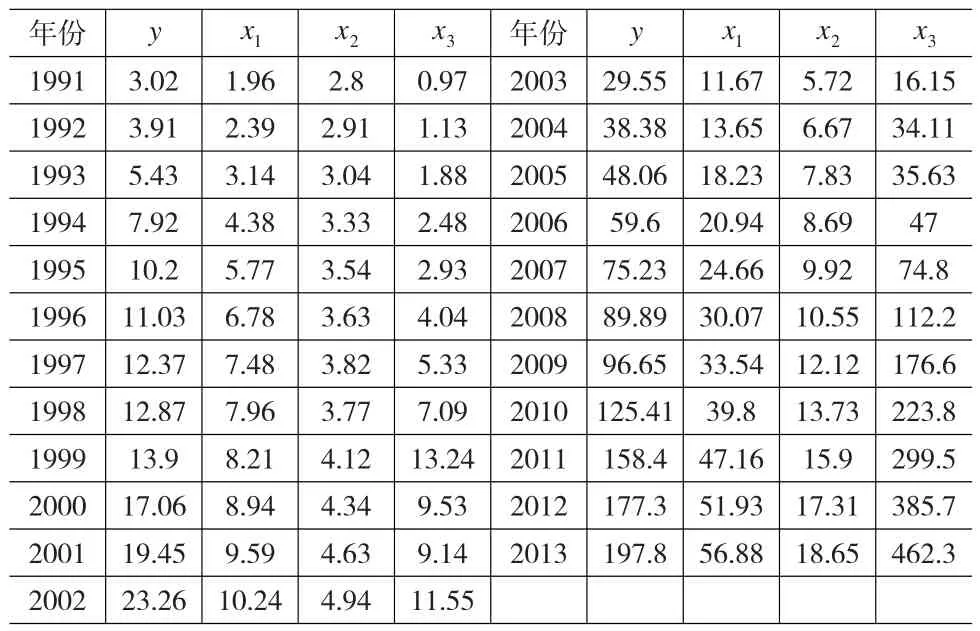
表1 1991～2013年各项统计数据

根据1991～2013年的统计数据，用SPSS软件进行回归分析，结果为：β0=-16.901，β1=0.899，β2=5.925，β3=0.116，相关系数 R=0.999，检验 F=3538.014，通过数学检验。回归方程如下：

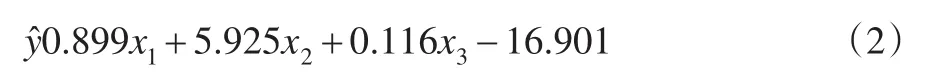
用差异分析法比较近两年的预测值与实际值，我们可以发现，该模型比较理想（表2）。

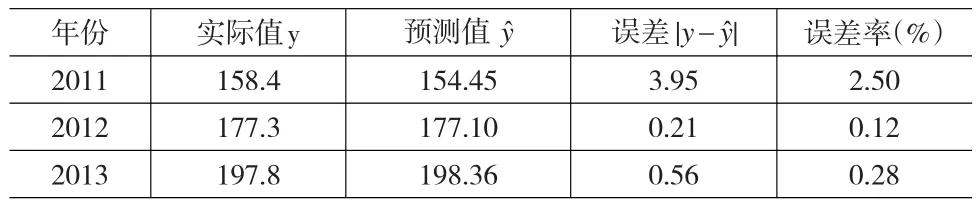
表2 比较预测值与实际值

目前，利用多元线性回归进行预测时，只要将确切的自变量预测值代入回归模型就可以预测出因变量的未来水平。但预测是对未来的判断，而未来宏观环境的变化是不确定的，自变量的预测值也会随着环境的这种不确定性变化而呈现出多个不同的水平，自变量未来的预测值并不是唯一的。而且，受到现有信息以及知识的限制，我们很难给出各预测值未来可能出现的概率，也无法通过计算期望值的方法得到确切的预测值。在这种情况下，试图用回归分析进行预测显然是行不通的。然而，根据客观经验以及相关调研分析，我们可以很容易地给出各自变量所有可能的组合的概率大小顺序，对于这类问题，可以考虑建立概率排序型预测模型来解决。

2 概率排序型预测方法建模

2.1 问题描述与假设

给出线性回归模型如下：

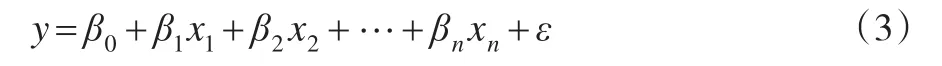
式中：y为因变量，x1，x2，…，xn为 y的n个关键影响因素，β1，β2，…，βn为参数，ε是随机误差。

表3 不同概率下各种组合及其对应的结果

由以上分析可知，在实际的预测分析中,决策者对未来各自然状态出现概率的了解是处于既有所了解但又不足以单值地计算出准确数值来。换言之，决策者只知道N个未来状态的概率将呈现出由大到小的顺序：p1≥p2≥…≥pN，而不知道 pi的具体数值。在这种情况下,拟用传统预测模型显然是不可行的，因而研究此类状态下的预测方法实用性很大，概率排序型预测方法正是这样一种方法。

2.2 模型的构建

在概率排序型预测中，由于各自然状态出现的概率大小无法准确估计，所以也无法准确计算其期望值，但是我们可以求得期望值的最大值和最小值，因此，以区间的形式来描述预测结果，不失为一个简单而又有效的办法。

因变量y的期望值E(y)的最大值和最小值为:

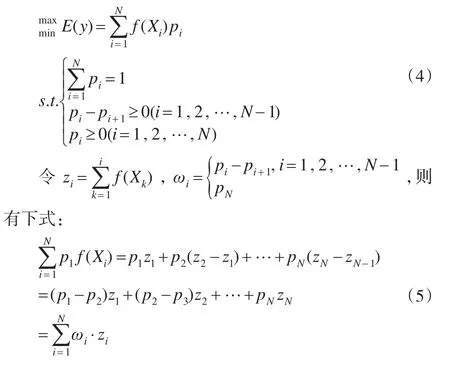
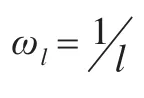
3 基于概率排序型预测模型的中国物流发展趋势分析

3.1 影响因素指标预测

任何事物的发展都受到宏观环境的影响，宏观环境的好坏决定了事物发展水平的高低。GDP、全社会货物周转量以及仓储业固定资产投资额作为三个经济方面的指标，其发展水平必然与我国经济发展情况这个大环境密切相关。由于未来经济发展具备不确定性，三个指标的预测值也可能随之出现不同水平的波动。为了充分考虑这种不确定性，将所有可能的情况考虑进来，在对影响因素指标进行预测时，应对未来经济形势乐观、正常和谨慎估计下三个指标的表现都有所涉及。

中国发改委主任在2011年称欧美账务危机增加了全球经济发展的不确定性，中国经济今后将进入“中速增长期”，即增长率会从前十年平均9%下降到7%左右，相比于9%的增长率，显然7%的增长率是个较为谨慎的估计。安永（美国会计事务所）则表示，尽管最近几年增长率有所下降，但中国经济发展的势头依然强劲，其乐观地估计我国GDP仍能够继续保持接近8.2%的平均增速；然而，从客观实际出发，更多的学者认为我国经济既不会继续高增长，也不会进入所谓“中速”增长期，而是会延续近几年的发展趋势，继续以7.5%左右的增速增长。

根据以上数据，可以计算出2011～2017年三种经济形势下中国GDP的预测值见表4所示，其中2011～2013年的数据用于检验模型，2014～2017年的数据用于预测，全社会货物周转量以及仓储业固定资产投资额的预测也如此。

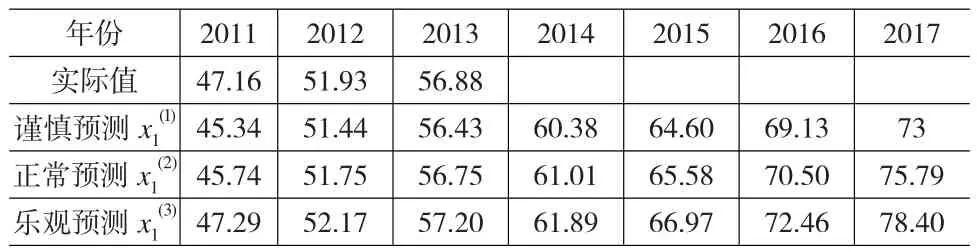
表4 2011～2017年中国GDP预测 （单位：万亿元）

文献[11]根据国民经济“三步走”的发展战略，提供了三种方法预测未来中国货物运输发展趋势，显然，货物运输发展水平也受到经济发展形势的影响。文献中预测结果是基于较早期的数据计算而来，故并不直接引用其数据，而只是借鉴其预测方法，并根据表1中的历史统计数据重新计算得来。对比三种模型的预测结果，灰色模型预测值最高，线性回归次之，指数平滑最低，因此，我们可将灰色模型、线性回归和指数平滑的预测结果分别认为是经济形势乐观、正常和谨慎情况下的预测。

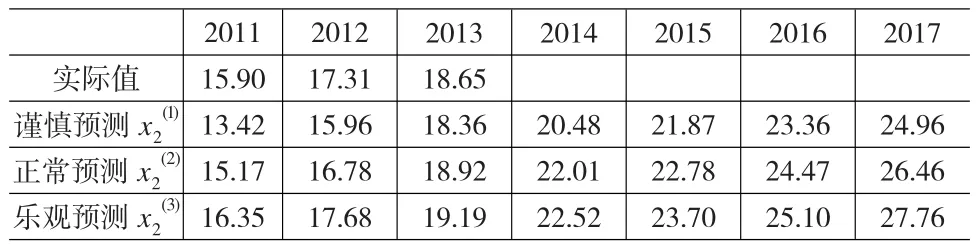
表5 2012～2017年全社会货物周转量预测 （单位：万亿吨公里）

现有资料中几乎没有涉及仓储业固定资产投资额的预测数据或者大都需要高价购买，我们很难找到权威的预测数据。考虑到我们已经搜集到的大量历史数据，可利用SPSS软件进行时间序列法预测，预测结果如表6所示。预测结果中给出了高、中、低三个水平的预测值，显然，预测值与投资者对未来经济形势的把握有密切关系，投资者认为未来经济形势乐观，预测值就高，对未来经济形势持谨慎的态度，预测值则低。

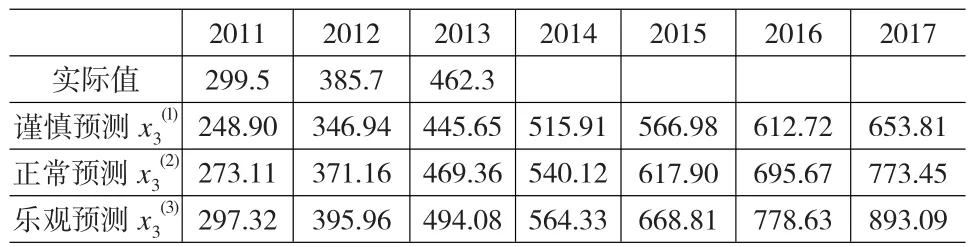
表6 2012～2017年仓储业固定资产投资额预测 （单位：十亿元）

3.2 概率排序

由上一节的分析可知，GDP、全社会货物周转量以及仓储业固定资产投资额指标各有三个不同水平的预测值，理论上三个指标的组合应该有3×3×3=27种。然而，三个指标都受到同一个宏观环境的影响，不同水平的预测值是基于对未来经济发展前景不同的预期而得来，因此，当人们对经济形势的发展前景持乐观态度时，对三个指标的预测都将是乐观预测；当人们对经济形势的发展前景持谨慎态度时，对三个指标的预测也都将是谨慎的；而不可能同时出现一个指标乐观，而另一个指标谨慎。所以三个指标的组合实际上只有N=3个，分别是：{谨慎，谨慎，谨慎}、{正常，正常，正常}、{乐观、乐观，乐观}。

由于未来经济发展具备不确定性，我们无法准确地估计未来经济发展形势乐观、正常和悲观三种情况可能出现的概率，但是根据相关资料，我们可以对三种情况可能出现的概率大小进行排序。英国广播公司国际部近期在全球25个国家所做的最新民意调查显示，中国人对长期经济前景持乐观态度的人占受访者的比例高达62%，对经济前景感到悲观的受访者比例仅占11%，剩下近30%的人对经济前景乐观或悲观并无太大倾向性，由此可知，我国经济前景乐观的概率最大，正常发展的可能性次之，发展前景悲观的概率最小。按可能出现的概率大小对表7中的组合进行排序，结果见表7所示。

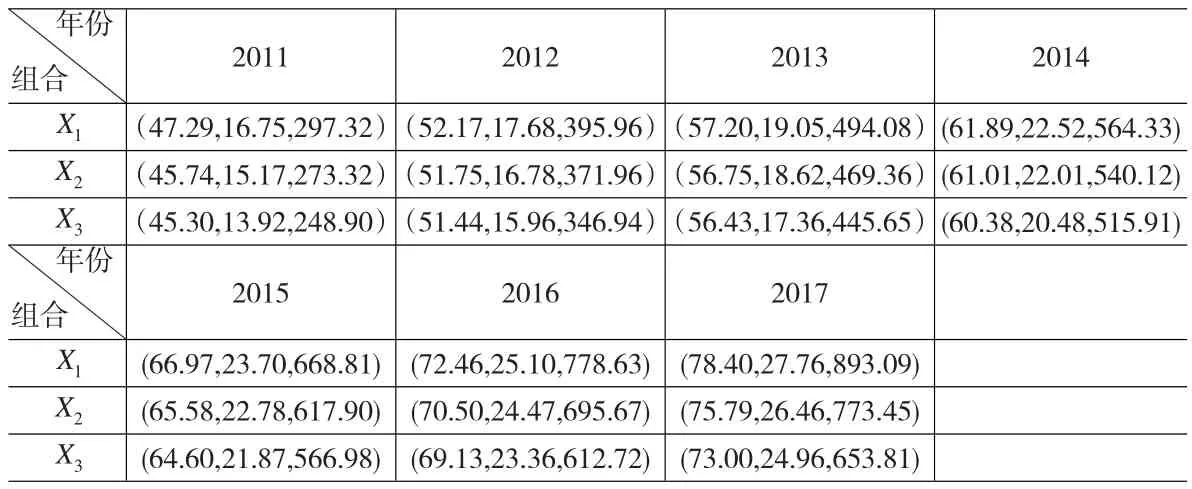
表7 2011～2017年组合概率排序

表7中显然有：p(X1)≥p(X2)≥p(X3)，这种情况可用概率排序法进行计算。

3.3 预测

由式（2）可知：

ŷf(x1，x2， x3)=0.899x1+5.925x2+0.116x3-16.901

每一个组合Xi(i=1，2，3)都唯一地确定一个y值。将每种组合的取值代入方程就得到相应的y值，如表8所示。

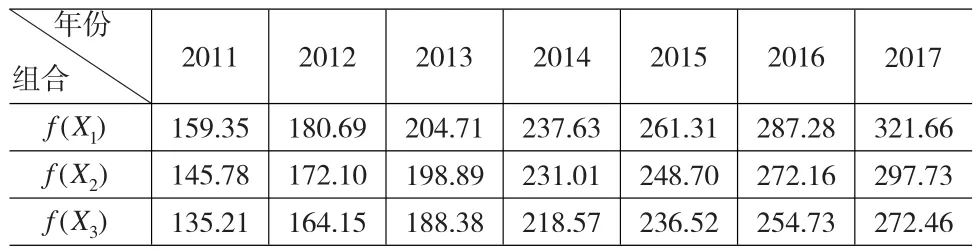
表8 2011～2017年概率排序下对应的预测y值

由第3部分的分析可知，求解y的最优期望值，只要计算出所有N个局部平均数，并且直接判断就可以找到最大期望值和最小期望值。最大的局部平均数就是期望值的最大值，最小的局部平均数就是期望最小值。根据此算法可求得2011～2017年社会物流总额的预测区间，预测结果见表9所示。对比2011～2013年的数据可知，实际数据均落在预测区间上，预测结果可靠。

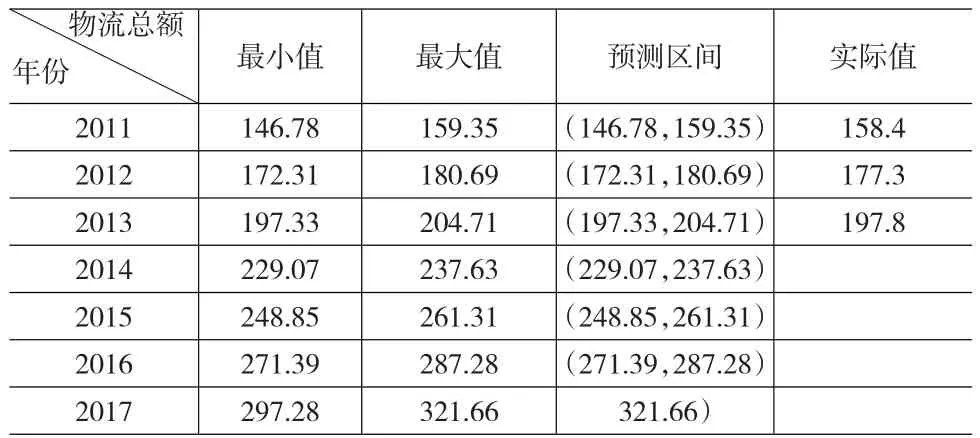
表9 2011～2017年社会物流总额的预测（万亿元）

3.4 结论与分析

通过上述计算，预计2104年社会物流总额为（229.07，237.63）万亿元，2015年会攀升至（248.85，261.31）万亿元，2016年为（271.39，287.28）万亿元，到2017年，电子商务交易额将在297.28万亿元与321.66万亿元之间。

根据表1中1991～2013年社会物流总额的历史数据以及表9中2014～2017年社会物流总额的预测数据（取最大值与最小值的均值进行计算），可做出1991～2017年社会物流总额的增长图如图4所示。

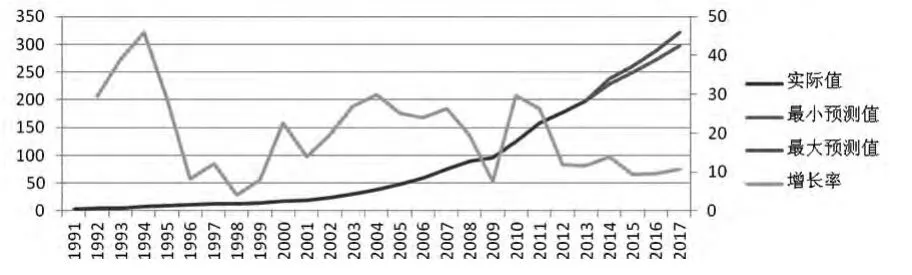
图4 1991～2017年社会物流总额及增长情况

由图4可知，在未来的四年中，社会物流总额呈逐年递增的趋势，2014年开始突破200万亿元大关，到2017年，甚至有望超过300万亿元可见中国物流业发展前景仍然十分乐观。

另外，观察社会物流总额的增长曲线可知，在过去很长的一段时间中，我国物流业发展很不稳定，增长速率波动较大，1994年增速达到了46%，而1998年的增速却只有4%，但总体上增长速率呈下降的趋势。随着物流在我国发展的时间越来越长，社会物流总额的增长速率也越来越平稳，近几年物流总额增长速率的波动远小于刚开始一段时间的波动。随着物流业的进一步展，社会物流总额的增长速率将逐渐变得较为平缓。在未来的四年中，社会物流总额的增长速率只有很小幅度的波动，增长速率大概在10%左右，未来几年中我国物流业或进入“中速增长期”。

4 总结

本文构建了物流业发展水平的回归预测模型，并结合概率排序的方法对我国未来4年物流业发展趋势进行了预测。概率排序法是一种仅需要根据各自然状态出现概率大小顺序的信息来进行预测的方法，而并不需要准确估计主观概率，选择概率排序方法预测我国物流业发展水平有效地弥补了研究中主观概率值缺失的缺陷，方法简单，应用方便。而且，在预测中概率排序法充分考虑了回归模型中自变量未来可能的波动水平，预测结果以最大和最小期望值的区间形式很好地描述了由于自变量的不确定性导致的预测值的波动性，预测结果更贴近实际，具有很强的现实意义。而且，目前在物流领域，甚至是其他领域，对概率排序方法的研究都较少，用概率排序法来解决物流业发展趋势的预测问题是一次新的尝试。

[1]Navickas,Valentinas,Sujeta,et al.Logistics Systems as A Factor of Country’sCom-petitiveness[J].EconomicsandManagement,2011,(16).

[2]Warren H H,Hau L.Lee,Uma Subramanian.The Impact of Logistics Performance on Trade[J].Production and Operations Management,2013,22(2).

[3]Dewan M Z,Islam J,Fabian M,et al.Zunder,Giuseppe Pace.Logistics and Supply Chain Management[J].Research in Transportation Economics,2013,(41).

[4]Intan M M,Sabri A.Stepwise Mu-ltiple Regression Method to Forecast Fish Landing[J].Procedia Social and Behavioral Sciences,2010,(8).

[5]王文贺,刘莉.多元回归分析法在城市用电量预测中的应用[J].沈阳工程学院学报(自然科学版),2012,8(4).

[6]周晓娟,景志英.基于多元线性回归模型的河北省物流需求预测实证分析[J].物流技术,2013,32(5).

[7]付玲馨,李晶.长沙市物流业需求预测与发展对策研究[J].科技视界,2013,(35).

[8]董安明.概率排序型决策的方法[J].安庆师范学院学报(自然科学版),2000,6(3).

[9]陈刚,蔡远利,穆静,杨卫丽.海量信息异常检测问题的异常概率排序算法[J].西安交通大学学报,2011,45(4).

[10]于百胜,黄文虎.不可能Hitting集的剔除与可能Hitting集的概率排序[J].振动工程学报,1997,10(3).

[11]龚树生,刘开明.我国物流统计发展现状分析[J].中国流通经济,2003,17(1).

[12]严季,王炼.我国货物运输发展趋势分析[J].武汉理工大学学报(交通科学与工程版),2003,27(6).