风暴条件下自升式平台桩腿强度对节距敏感性分析研究
朱亚洲 孙承猛 王 凯 樊岩松 秦洪德 姜 滨
(1.哈尔滨工程大学 船舶工程学院 哈尔滨150001;2.中国石油集团渤海装备 辽河重工有限公司 盘锦124010)
引 言
自升式平台是当今海洋油气开发的主流装备,因其移动灵活,作业稳定、造价较低等优势备受广大钻井承包商亲睐[1]。目前自升式平台作业水深基本集中在90 m以内,且以15 m为步长,基本覆盖了76 m、90 m、107 m、122 m系列型号,上述型号已初步形成较为稳定的结构形式。近年来,为提升平台经济性,适应更细化水深要求的自升式平台需求显著,对新型号自升式平台的设计提出新的挑战。本文以114 m作业水深的自升式平台为目标,对其桩腿结构单元节距设计技术进行研究,采用SESAM软件,研究在风暴条件下的自升式平台桩腿节距设计方法,为个性化平台的设计提供技术参考。
1 环境载荷
环境参数是任何一座海洋结构物设计初始需要确定的外界输入之一。本文以风暴环境条件为外界输入,选取三种作业水深及其对应的气隙和波高条件进行组合,假设浪向和风向一致,以0°、60°、90°、120°和180°风向和浪向进行计算,假设波浪周期不随波高和水深变化,选取目标平台作业海域的波浪周期统计数据15 s进行计算,具体参数见表1。

表1 风暴条件环境参数
1.1 风载荷计算
自升式平台风载荷计算方法主要包括经验公式法、数值模拟法和风洞试验法[2-4]。经验公式法计算简单方便,但由于仅考虑构件高度系数和形状系数对载荷的影响,并没有计及构件之间遮蔽效应等因素的影响,导致风载荷计算结果偏大,结构设计偏于保守[5]。风洞试验方法是公认的自升式钻井平台风载荷计算方法,试验结果接近真实,较为可靠,但国内外关于此类问题研究较少[6]。数值模拟方法介于规范计算和风洞试验两者之间,基于CFD计算方法,完成风载荷计算,此方法计算结果对流场参数选取较为敏感,其经济性较好[7]。
本研究采用在某国家重点试验室模拟的我国A类地表自然流场的TJ-2风洞中按1/100缩尺比模型进行五分量测力试验,对目标平台在风暴条件下的风载荷进行测量,测试时参考高度href=10 m处风速为51.5 m/s(100 kn)的研究结果,每隔15°为偏角方位,模型在水平面内360°旋转。

图1 风洞模型
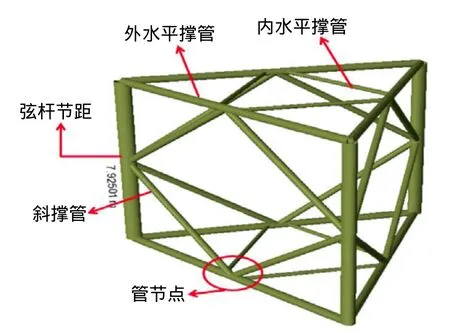
图2 桩腿节距内参数化设计有限元模型
1.2 波流载荷计算
波浪载荷是自升式平台仅次于风载荷的第二主控载荷,波浪载荷的计算首先需要确定选用适当的波浪理论,本文采用STOKES五阶波理论得到波浪水质点运动的速度势或者流函数[8-11],进而得到水质点运动的速度和加速度,由于桩腿结构为小尺度结构型式,因此采用MORISON方程[12]计算波浪载荷。MORISON公式表达如下:

式中:η为瞬时波面高度,m;d为水深,m;Cd为水质点拖曳力系数;Cm为水质点惯性力系数;ρ为流体密度,kg/m3;D为柱体直径,m;u为水质点运动速度,m/s。
海流速度受潮汐、涌和风等因素影响,根据平台作业海域的不同,流速随水深分布可按三角形分布或指数函数分布[13]。在进行环境载荷计算时,可将流速和波浪引起的水质点运动响应进行叠加,组合计算波流载荷。ABS的流速计算推荐公式[14]:
当z≤h时,Vc=Vt+Vs+Vw[(h-z)/h];
当z>h时,Vc=Vt+Vs
式中:Vt、Vs和Vw分别为潮汐、涌和风引起的流速,m/s;h为风对浪的作用深度,m;z为参考深度,m。
通过上述流速计算,同样可以通过MORISON方程,给出流载荷计算公式:
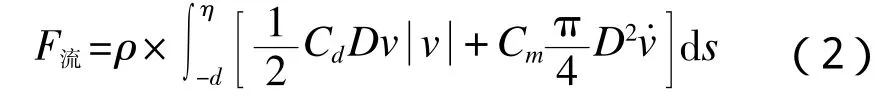
式中:v为海流速度,m/s。
则可将波浪载荷和海流载荷结合在一起进行计算,统一到波流载荷计算公式中[13]:
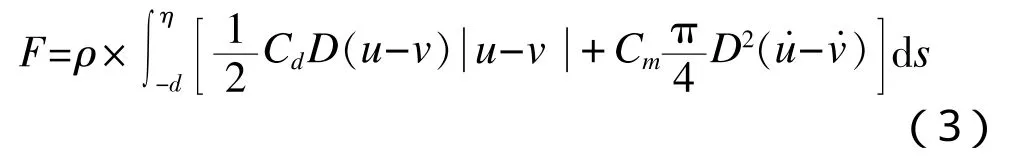
本研究采用SESAM软件的WAJAC模块计算既定工况条件下的水动力载荷。
1.3 DAF效应
自升式平台水动力放大系数的计算可采用时域分析、频域分析和单自由度SDOF方法求解[15]。本研究将平台系统简化为单点质量-阻尼-弹簧系统,采用SDOF方法,求解平台桩腿结构在水质点往复周期性外力作用下的水动力放大系数DAF。
式中:TN为平台固有周期,s;T为波浪周期,s;ε为阻尼比,取0.07。当DAF≥1.05时,需要计及惯性载荷影响,惯性载荷计算公式如下:

式中:BSmax为最大波浪力;BSmin为最小波浪力。
通过SESAM软件GeniE模块进行特征值分析,得出不同节距条件下的平台固有周期,进而可以得到DAF因子,结合最大和最小基底剪力,采用公式(4)和公式(5)计算,得到计及DAF效应的惯性载荷[16-17]。该方法可有效规避平台固有周期与波浪周期接近引起的共振效应对平台结构的影响。
1.4 P-△效应
对于大水深自升式平台而言,较长的桩腿结构柔性特性显著,在外载荷作用下,平台主体结构发生横向偏移,桩腿与主船体连接区域将产生较大的附加弯矩,导致桩腿截面出现二次应力作用,此种情况下传统的线弹性小变形有限元程序分析方法已不再适用,一般采用大变形方法或几何刚度法[16-17]。本研究采用几何刚度法分析P-△效应,通过放大线弹性位移确定,公式如下所示:
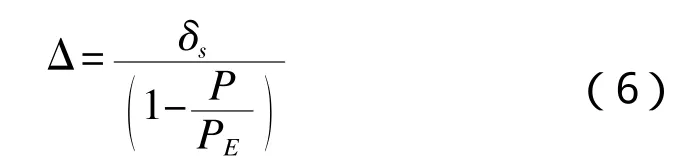
式中:Δ为含P-△效应的近似位移,m;δs为主船体线弹性一阶位移,m;P为单桩腿轴向载荷;PE为单桩腿欧拉屈曲载荷。
等效弯矩计算公式如下:

等效二次力的计算由下式得出:

式中:H为作用力至泥面的垂直高度,m。
2 有限元计算
采用SESAM软件GeniE模块建立自升式平台有限元模型,对主船体结构纵横舱壁采用等效截面梁的形式进行模拟,并以质量球的形式施加结构自重,桩腿弦管单元采用等效梁进行模拟,撑管单元以实际尺寸的梁单元进行模拟。
桩腿底部边界条件依据规范取泥线下3.05 m处铰支[16]。桩腿与主船体的连接模拟是桩腿弦管与围阱区上、下导块和锁紧结构的三点连接,上下导块只约束水平位移,锁紧位置同时约束水平和竖直位移。
以114 m作业水深的自升式平台为研究对象,型长68.15 m、型宽66.10 m、型深8.30 m、悬臂梁最大外伸21.4 m、桩腿长度155.57 m、平台质心距外底板基线垂向高度10.779 m、空船质量12 564 t。
本文主要针对桩腿结构节距变化对强度的影响进行分析,表2为桩腿构件设计参数。
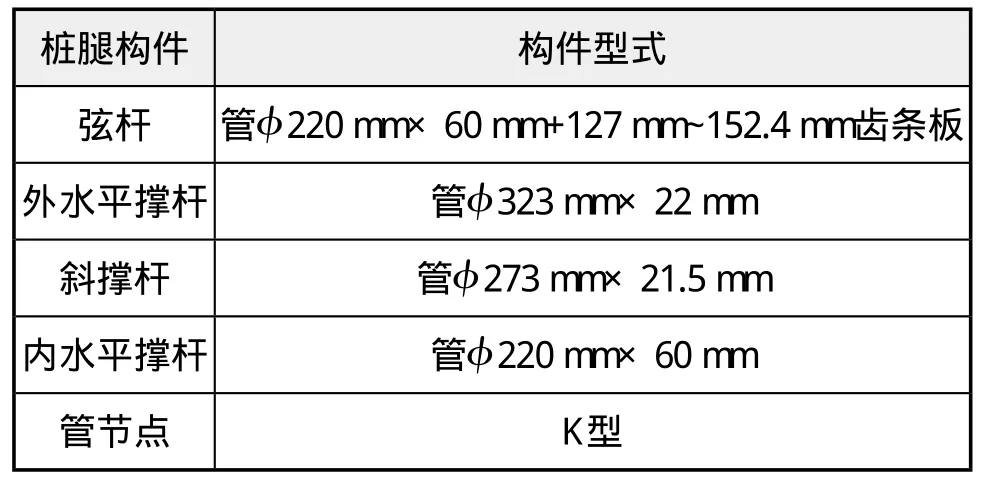
表2 桩腿构件设计尺寸表
结合主流平台桩腿节距值,本研究对目标平台桩腿节距分别取值为:7.090 m、7.485 m、7.935 m、8.420 m、8.980 m,不同节距型式下的桩腿质量估算如表3所示,采用参数化建模方法对上述五组节距形式下的桩腿在风暴环境条件下的承载能力进行评估,给出平台桩腿节距设计最优方案,通过SESAM软件模态分析得到的3种工况在不同节距型式下的平台固有周期如表4所示[18]。

表3 不同节距对应的桩腿质量s
本研究采用的风载荷来自于风洞试验结果,假设不考虑节距变化对风载荷影响,仅计及节距变化对平台DAF因子影响,得出环境载荷如下:
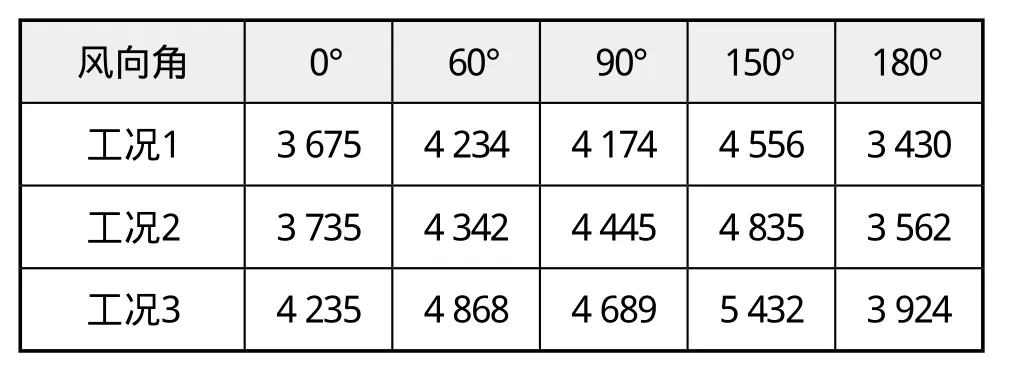
表5 风暴环境条件下风载荷计算表(风洞试验数据)

表6 计及DAF效应的环境载荷计算表(工况1)

续表6
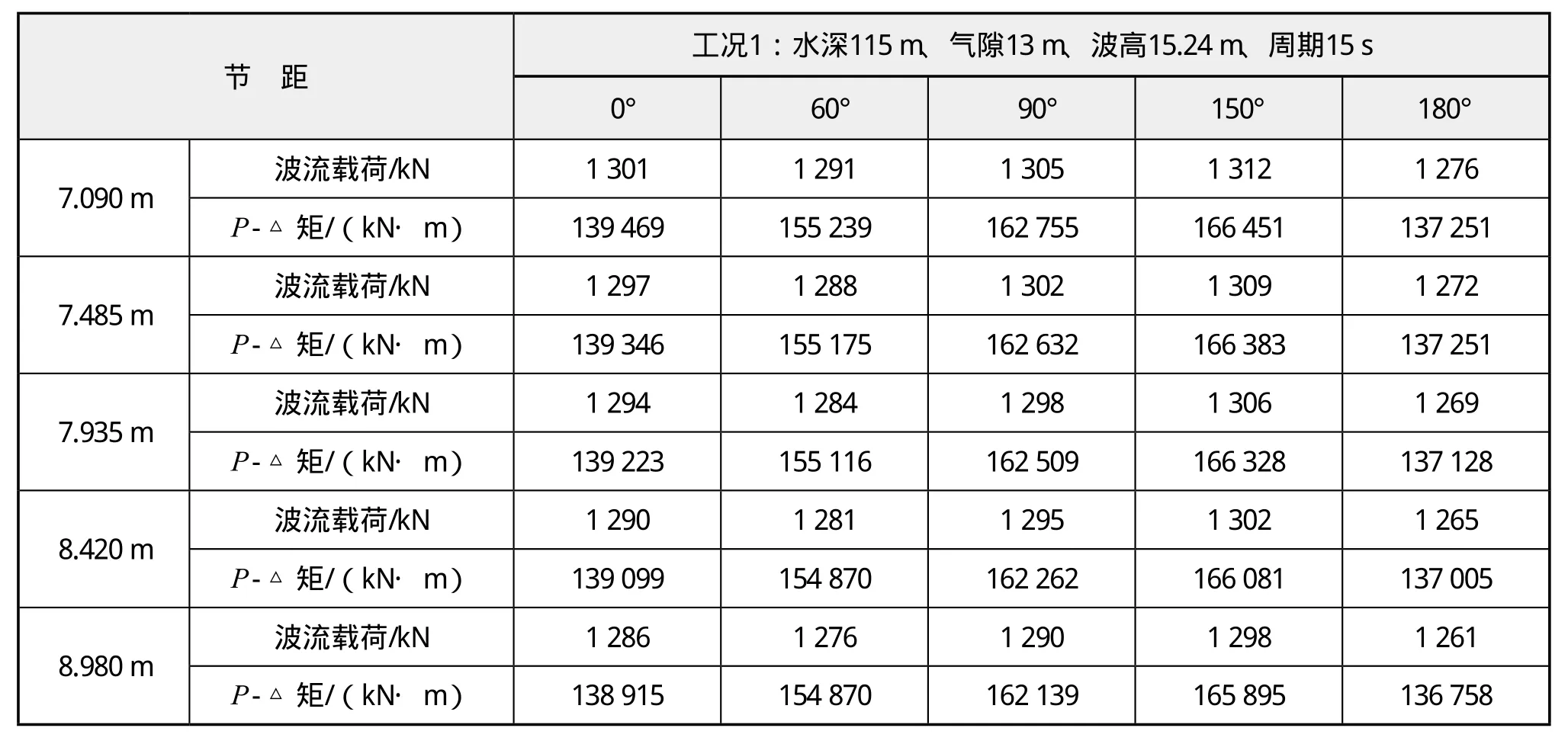
表7 计及DAF效应的环境载荷计算表(工况2)
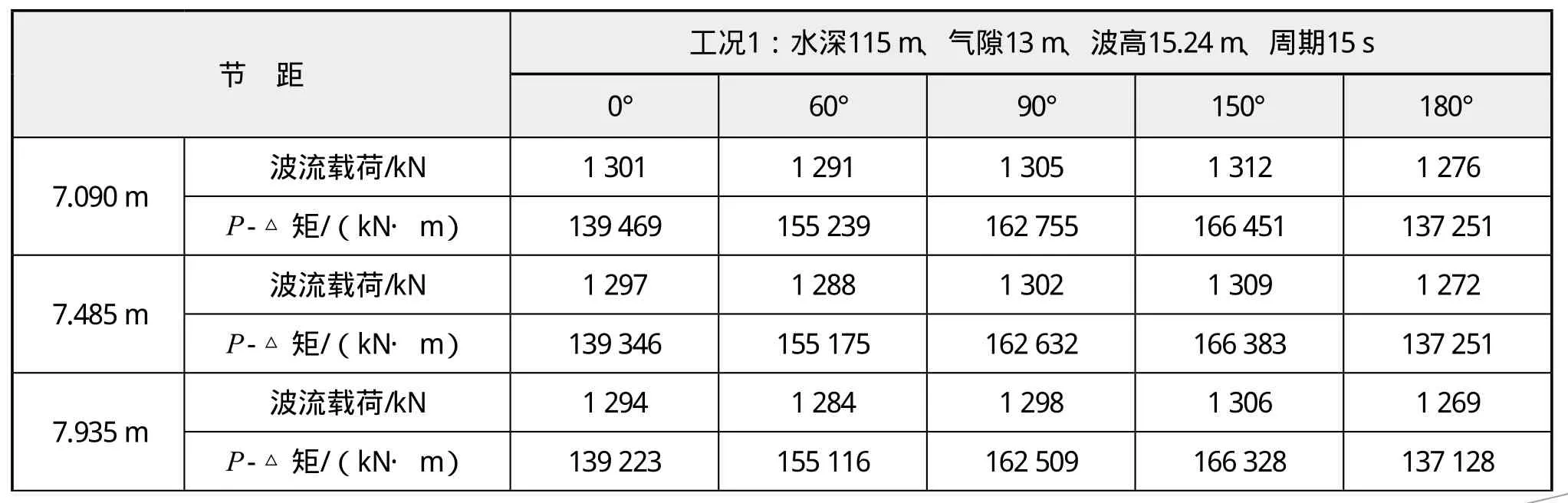
表8 计及DAF效应的环境载荷计算表(工况3)
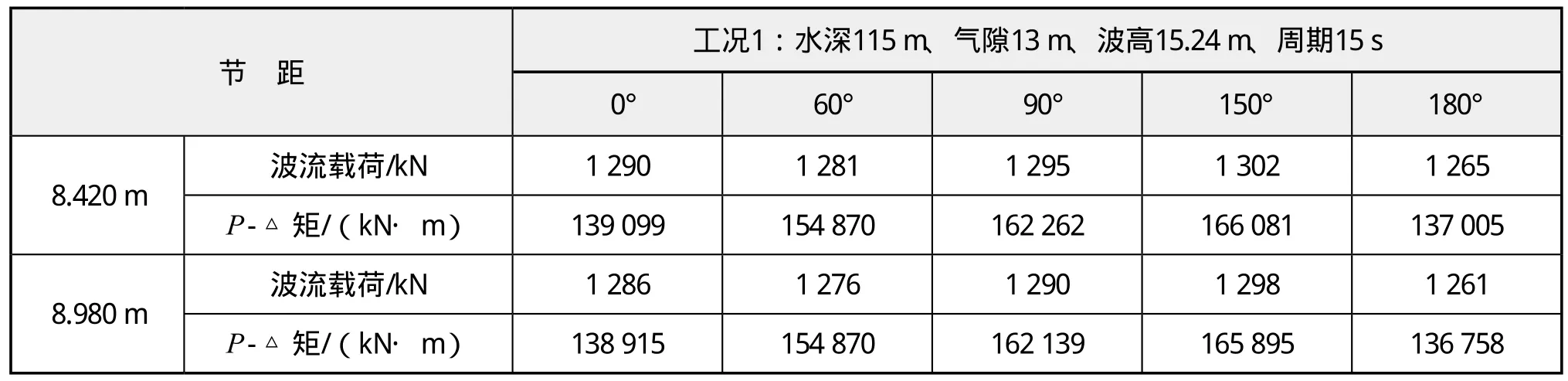
续表8

图3 工况1:波流载荷数据统计柱状图
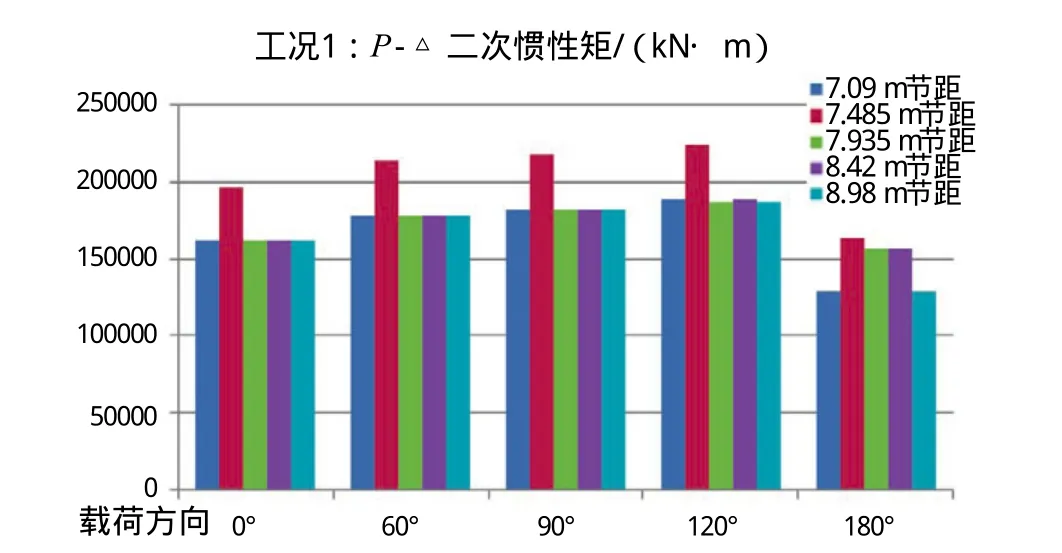
图4 工况1:P -△矩数据统计柱状图
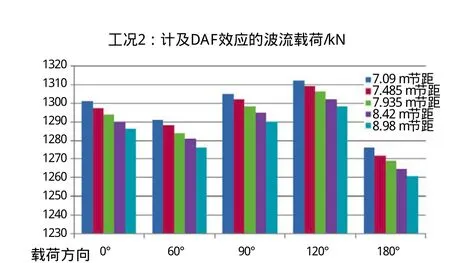
图5 工况2:波流载荷数据统计柱状图
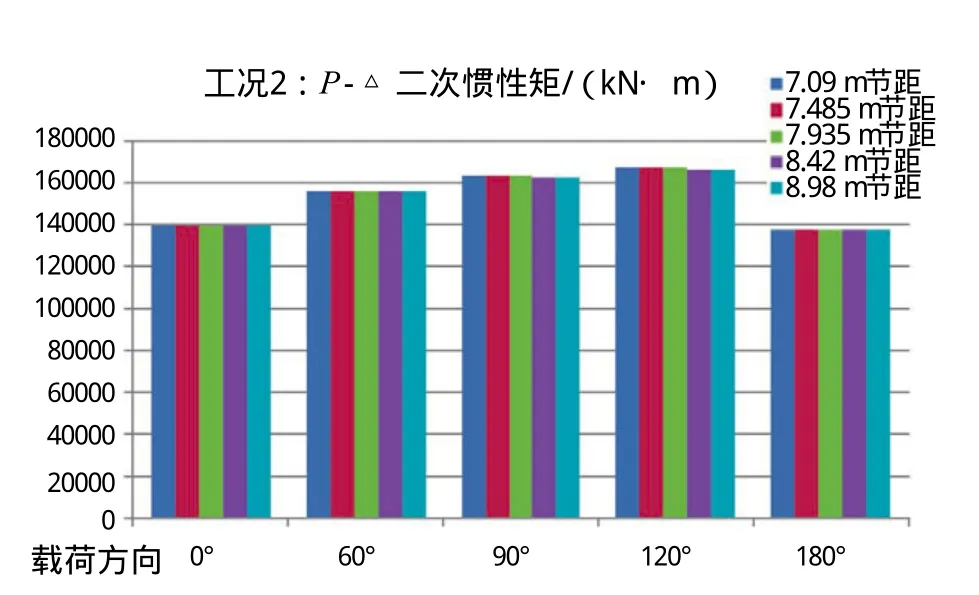
图6 工况2:P -△矩数据统计柱状图
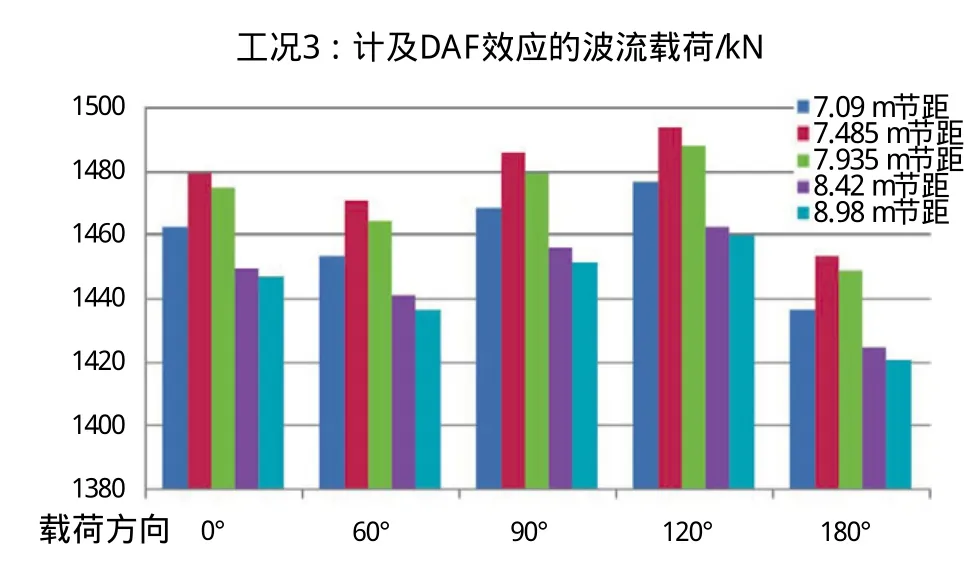
图7 工况3:波流载荷数据统计柱状图

图8 工况3:P -△矩数据统计柱状图
3 结果分析
3.1 载荷比较分析
由表5-表8统计的载荷计算结果比较分析可知,随着节距变大,波流载荷呈递减趋势,二次惯性矩随节距变化趋势平缓。
(1)在工况1条件下,波流载荷在桩腿节距7.485 m时,由于平台固有周期接近波浪周期,如表4所示,导致水动力放大效应引起的惯性载荷显著增大,同时引起P-△二次惯性矩跳跃式增加,不利于结构安全。因此,对本平台而言选取7.485 m节距不安全。
(2)在工况2条件下,波流载荷随节距增大呈逐级递减趋势,P-△二次惯性矩几乎不受节距变化影响,仅对载荷方向变化较为敏感。因此,对本平台而言在此工况下选取较大节距,载荷条件较优。
(3)在工况3条件下,节距取值7.485 m和7.935 m时,波流载荷逆势小幅增大,P-△二次惯性矩受节距变化影响可以忽略不计。因此,对本平台而言此工况下,基本验证工况2下的波流载荷变化趋势与节距的关系,即随着节距变大,波流载荷呈递减趋势,二次惯性矩随节距变化趋势平缓。
3.2 结构强度比较分析
通过有限元软件对桩腿结构各组成单元强度进行校核,对结构UC值列图如下:
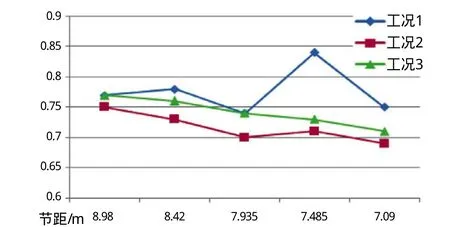
图9 桩腿弦管有限元计算UC值
(1)由图9分析可知,弦管结构在工况1条件下,节距取值7.485 m时UC值达0.84,比较危险,节距取值7.935 m或7.09 m较为理想。
(2)由图10分析可知,外水平撑管在工况2条件下,节距取值8.98 m时UC值达0.23,虽然满足安全要求,但相对同类结构在其他节距时的UC值增幅明显,因此,节距8.98 m不是优选节距。
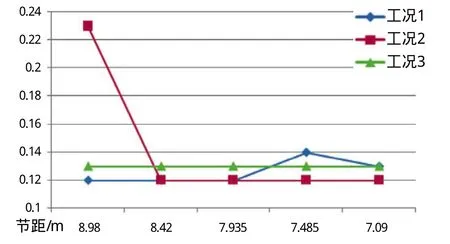
图10 桩腿外水平撑管有限元计算UC值
(3)由图11分析可知,斜撑管在工况1条件下,节距取值7.485 m时UC值达0.58,节距取值7.09 m时的UC值也高于节距取值7.935 m时的UC值,即7.935 m节距优于7.09 m节距。
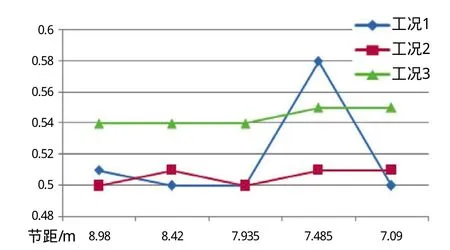
图11 桩腿斜撑管有限元计算UC值
(4)由图12分析可知,桩腿水平内撑管UC值受节距变化影响不大。
(5)由图13分析可知,撑管接头是有限元分析主要关注的区域,综合分析可知7.935 m节距为最优节距。
结合上述不同桩腿节距形式针对载荷影响及对结构强度校核UC值的影响分析,综合考虑桩腿质量变化趋势(如表3所示),本平台确定7.935 m为桩腿节距最优尺寸。
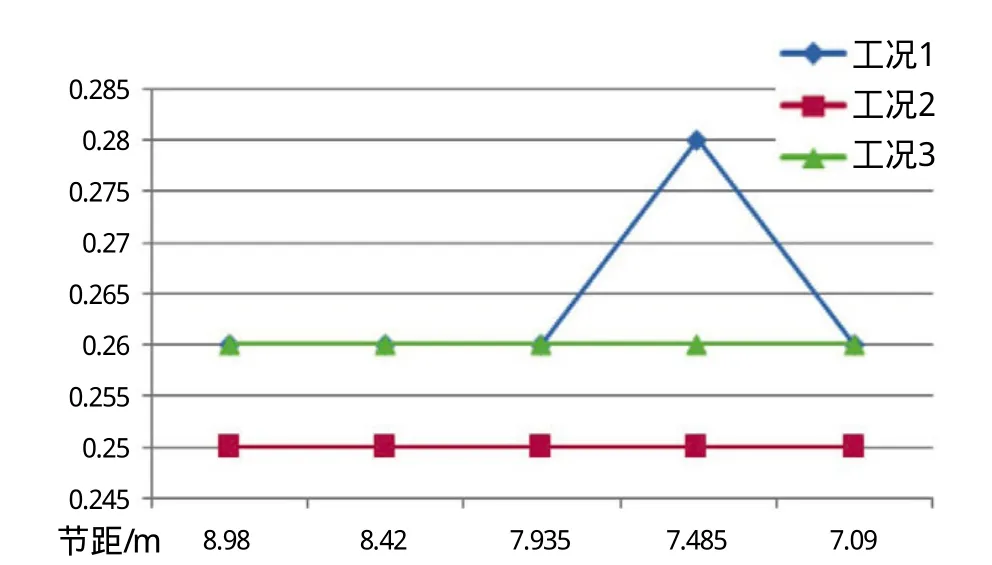
图12 桩腿内水平撑管有限元计算UC值

图13 桩腿管节点有限元计算UC值
4 结 论
本文针对目前稀有型号114 m作业水深自升式平台桁架式桩腿结构节距优化设计技术进行研究,完成风暴条件下桩腿强度对节距敏感性分析。通过风洞试验与STOKES五阶波理论等试验与理论研究,采用SESAM软件进行特征值分析,得出计及DAF水动力放大效应和P-△二次惯性效应的载荷数据,并重点对不同节距形式的桩腿结构强度进行对比分析,如弦杆结构、外水平撑管、内水平撑管、斜撑管和重要管节点结构等,确定目标平台节距优选值,形成桩腿强度对节距敏感性分析技术,为该稀有型号平台核心部件的自主设计提供技术参考,并可为广大工程技术人员实现桩腿结构优化设计提供技术依据。
[1] Zhu Yazhou,Sun Chengmeng,Qin Hongde,et al.,Study on Design Technology of Jack-up X-Type Cantilever Allowable Load Nephogram [J].Journal of Marine Science and Application (2014)13:315-320.
[2] 谭美,冯军,熊飞.自升式钻井平台风载荷研究[J].船舶与海洋工程,2014(1):18-23.
[3] 林一,胡安康,熊飞.自升式平台风载荷数值模拟与试验研究[J].水动力学研究与进展,2012(2):208-215.
[4] 朱航,马哲,谢彬,等.梯度风作用下HYSY-981半潜式平台风载荷与表面风压分布研究[J].中国海上油气,2010(4):270-274.
[5] Aguirre J E,Boyce T R.Estimation of Wind Force on Off shore Drilling Platforms[J].The Naval Architect,1974.
[6] 林一,胡安康,孙建.自升式平台风载荷的空气动力学干扰研究[J].船舶与海洋工程,2013(2):5-10.
[7] 林长刚.自升式海洋平台风载荷及风暴环境图谱研究[D].大连理工大学硕士学位论文,2013.
[8] 汝建,贾忠红,邢惠利.浅海结构物波浪力计算及实验研究[J].中国海上油气(工程),1999(6):23-30.
[9] Sarpkaya T,Isaacson M.Mechanics of WaveForces on Offshore Structure [M].New York,VanNostrand Reinhold Co.,1981:473-563.
[10] Skjelbreia L,Hendrickson J A.Fifth OrderGravity Wave Theory and Tables of Functions [M].National Engineering Science Co.,Pasadena,1962.
[11] 竺艳蓉.海洋工程波浪力学[M].天津:天津大学出版社,1991.
[12] 朱克强,刘永林,魏跃,等.近海结构任意倾斜桩腿的非线性波浪载荷计算[J].港工技术,2007(5):1-3.
[13] 高畅.自升式平台桁架腿波流载荷分析与实验研究[D].天津大学硕士学位论文,2010.
[14] ABS.Rules for Building and Classing Mobile OffshoreDrilling Units[S].2014.
[15] 吴小平,陆晟.自升式钻井平台环境载荷及结构强度[J].上海造船,2010 (3):36-41.
[16] DNV.Recommended Practice DNV-RP-C205.EnvironmentalConditions and Environmental Loads[S].2012.
[17] SNAME.Technical and Research Bulletin 5-5A SiteSpecific Assessment of Jack-Up Units[S].2007.
[18] 孙雪荣.拖航状态的自升式平台桩腿强度分析[J].船舶,2014 (1):49-52.

