数独游戏的问题生成及求解算法优化

黄祖贤

(中南大学信息科学与工程学院，长沙410012)

数独游戏的问题生成及求解算法优化

黄祖贤

(中南大学信息科学与工程学院，长沙410012)

将“数独”问题分解为建立终盘、生成有唯一解初盘和求解初盘等子问题。运用拉斯维加斯随机算法思想结合回溯法建立终盘，采用“挖洞”思想隐去部分数字并结合反序回溯法生成具有唯一解的初盘,依据初盘中空格数的多少对问题的难度进行划分，创建不同等级难度的“数独”游戏，并对求解数独问题的候选数搜索算法进行优化改进。实例分析结果表明，优化后的候选数搜索算法性能提高了50%以上，验证了所提出算法模型的有效性。

数独；回溯法；唯一解；候选数；搜索算法

数独是1种利用简单逻辑推理就能解决的数字谜题，其雏形源于1979年美国的数学逻辑游戏杂志—Dell Pencil Puzzles&Word Games发表的称之为“NumberPlace”的游戏[1-2]。目前，数独作为1种智力游戏已经风靡世界，其游戏规则为：在由9个小宫格组成的大九宫格(9格×9格)里，根据已知数字，利用逻辑和推理，填出剩余空格的数字1～9，且每个数字在其所在的行、列和小九宫格中出现且只出现1次[3]。初始数字的多寡与位置，一定程度上决定着题目的难易程度以及解是否能够唯一[4]。有学者认为通过对数独游戏的思考能够降低老年痴呆和帕金森综合症的患病率[5]，因此数独游戏吸引着无数“独迷”参与。

目前，许多学者对数独的求解与生成算法进行了深入研究，如，胥剑[6]使用回溯法快速求解数独问题，薛源海等[7]提出基于“挖洞”思想运用反证法判断解的唯一性，并对其进行剪枝优化，达到了较好的性能。候选数搜索法在求解数独问题上也有广泛的应用，常见的方法有唯一候选数法、隐形唯一候选数法和区块删减法等[8]。文中根据数独求解规则，对在终盘的基础上生成的数独初盘可能出现的不同解进行分析，采用反序回溯法检验初盘解的唯一性，并对传统的候选数搜索算法进行优化改进。

1 数独求解规则

数独必须遵循逻辑性、可推导性等原则，在求解数独时，必须让每一步有规可循，每一步推导有根有据[5]。数独展开逻辑推理需确保：数字1～9在每一行中各出现且只出现1次；数字1～9在每一列中各出现且只出现1次；数字1～9在每一个小九宫中，各出现1次且不重复。数独求解规则的实现步骤如下：

1)当前格子不为空，则返回FALSE；

2)将所选数字与该格同行同列的数字进行横向和纵向比较，若存在某数与所给参数数字相等，则返回FALSE；

3)将所选数字与该格所在宫格的数字进行比较，若存在某数与所给参数数字相等，则返回FALSE；

4)返回TRUE。

2 生成算法

2.1 终盘生成

2.1.1 基于小数的回溯法

基于小数的回溯法采用从左至右、从上至下的搜索方式，从初盘的第一个空格开始，由1到9搜索满足约束条件的1个解，以该可能解为出发点，对下一个空格继续进行由1到9的试探性搜索，如果在某一次搜索中某一空格的所有可能解都不能满足约束条件，则返回上一个空格，放弃原有的可能解，使用该空格的下一个可能解。依次类推，直到所有空格的可能解都被找到，则得到了该问题的一个完整解[6]。其算法步骤如下：

1)判断数独最后一行是否已填写完，如果是，则跳至步骤4)。否则，自左向右、自上而下搜索下一个空格；

2)由1到9遍历搜索，与该空格所在行、列以及所在宫的其他有效数字进行比较，若存在1个数满足约束条件，则将该数字填入该空格，跳至步骤1)；

3)若该空格的所有可能解都不能满足约束条件，返回上一个空格，其值重置为0，搜索并使用该空格的下一个可能解，并将该数字填入该空格，跳至步骤1)，否则继续执行该步骤；

4)输出1个数独终盘。

2.1.2 拉斯维加斯算法

采用拉斯维加斯算法随机生成1个数独题的终盘。首先，在1个数独“空盘”中随机选中n个格子，在这些格子内随机填入数字1～9；然后，调用上述求解器对已知n格的数独题S(n)进行求解。完成上述两步操作的JAVA代码段为BOOL Las-vegas(n)：如果S(n)有解，则返回TRUE；否则返回FALSE。拉斯维加斯算法的思想便是不断重复执行Las-vegas(n)，直至其返回TRUE为止，用JAVA编程语言表示如下

根据拉斯维加斯的算法思想可知，代码段Las-vegas(n)返回TRUE（即成功生成终盘）的概率p与n有关。已有研究表明[7]，当n=11时，p能达到0.997，且p随着n的减小而增大，但运行时间延长。故将n设为11。

2.2 有唯一解初盘的生成

基于“挖洞”思想生成有唯一解的初盘。“挖洞”思想就是“挖去”数独终盘上的一些格子，使其成为至少有1个解的数独问题。“挖洞”的机制多种多样，国内现有的研究中，多将其与数独问题的难度等级划分结合，生成有解初盘[7]。文中借鉴这一思想，采取1种较为简单的“挖洞”机制。“挖洞”流程中的关键问题如下。

1)“挖洞”数目

“挖洞”数目由保留格子的数目决定。文中简化了对数独问题的难度划分标准，以初盘上非空格的数量为依据、在一定区间内将数独问题划分为5个难度等级，如表1。

2)“挖洞”约束

从已知格的分布入手，对“挖洞”操作加以约束。规定，数独初盘中每行已知格的数目至少为2个，则已知格的总数至少为18个，因为[20，24]区间的整数均不能被9整除，所以各行不可能均多出1个已知格，只能有些行多1个或2个、有些行不增加，即每行至多有4个已知格。

用1个整型一维数组already[9]存储每行中已知格的数目，定义1个整型二维数组displayed[9][4]存放每行已知格的位置信息(随机产生，数组内的无效位置信息置“-1”操作“挖去”格子)，将数组外其他位置的格子“挖去”。实例如图1，2。

图1直观描述了一维数组already和二维数组displayed的对应关系，图2中灰格为由displayed确定的数独初盘上已知格的位置，白格为被“挖去”的格子。

表1 难度等级对应的“挖洞”数目Tab.1 Difficulty level corresponding to the number of holes

3)基于大数(反序)的回溯法解唯一性的判断

借助数独问题求解算法—回溯法提出1个新的策略来检验“挖洞”后的数独初盘是否具有唯一解。数独终盘中，对某几行或某几列的2个数(或多个数)的位置同时进行两两替换，得到的仍然是1个满足约束条件的数独终盘。可以推断，对于“挖洞”后的数独初盘，若存在多个解，则一定存在某些数字相对原终盘出现两两替换的现象。文中提出基于大数的回溯法对“挖洞”后的初盘进行求解用以检测上述情况中的多个解，其算法步骤为：

(1)判断数独最后一行是否已填写完，如果是，则跳至步骤(4)。否则，自左向右、自上而下搜索下一个空格；

(2)由9到1遍历搜索，与该空格所在行、列以及所在宫的其他有效数字进行比较，若存在满足约束条件的数，则将该数字填入该空格，跳至步骤(1)；

(3)若该空格的所有可能解都不能满足约束条件，返回到上一个空格，其值重置为0，搜索并使用该空格的下一个可能解，并将该数字填入该空格，跳至步骤(1)；

(4)输出数独终盘，若该次求解输出的终盘与原终盘有异，则重复进行新的“挖洞”约束。即一旦出现其他解，就放弃现有初盘，这在一定程度上降低了算法的复杂程度。

采用该算法与基于小数的回溯法对“挖洞”后的初盘进行求解，结果如图3。比较图3(a)，(b)可以发现，2种算法求解出的结果不同，在基于小数的回溯数独生成算法下，基于大数的回溯算法能够有效检测出某一“挖洞”初盘的多个解。

采用基于大数的回溯算法生成具有唯一解的初盘过程如图4。第三次“挖洞”后得到唯一解初盘如图4(c)，图4(a)是对第一次进行“挖洞”得到的初盘进行唯一解判断的结果。比较图4(a)，(c)中圈出部分可知，与原初盘有异，该初盘不可用。同理，由图4(b)知，第二次进行“挖洞”得到的初盘仍不可用。图4(c)显示了第三次进行“挖洞”后具有唯一解的初盘，表明该判断结果有效可信。

3 候选数优化

国内已有研究将基于人工智能的候选数法与回溯法相结合求解数独问题，其候选数优化算法相较于回溯法，缩短的时间至少为1/3[9]。文中采用相似的策略进行数据结构的设计，从候选数最少的空格出发，对候选数法进行优化以进一步提高求解速度。候选数优化过程的关键步骤。

1)求出候选数集 以候选数法求解数独问题时，必须明确数独初盘中每一个空格的候选数集合。产生候选数集合的方法是从1到9搜索，将满足约束条件的数存入候选数集合中。用一维整型数组c存放候选数集合，一维整型数组d存储该宫格的位置信息，d数组的长度比c数组的长度多2，其中d[0]和d[1]用来存储该空格的行、列值，随后存储该宫格的候选数集合。

2)找出候选数最少的集合信息 利用JAVA编程语言中Vector向量的特性，将数独布局中从上至下、从左至右每一个空格的d数组存入Vector＜int[]＞testVector容器中，对该容器中各候选数字集合进行排序，找到候选数字最少的集合及其在容器中的位置，并返回容器中该位置的数组。

3)候选数字回溯 在步骤2)中获取的候选数字最少的空格内将该数字格的候选数从小到大依次代入，每次代入后根据新的数独布局更新候选数集合并重新找出新布局下候选数最少的集合信息，若该集合长度为2(即只含有空格的行、列值信息)，则产生矛盾，进行回溯。这样，有效降低了回溯中枚举的次数。优化前，候选数法和回溯法的结合是简单的，没有为候选数集合进行排序选择的过程。

世界上迄今难度最大的数独游戏问题如图5[10]，在操作系统Windows 8.1和CPU为Intel Core i5(1.70 GHz)的环境下，采用优化前、后的候选数法分别对图5所示问题进行5次求解实验，结果见表2。

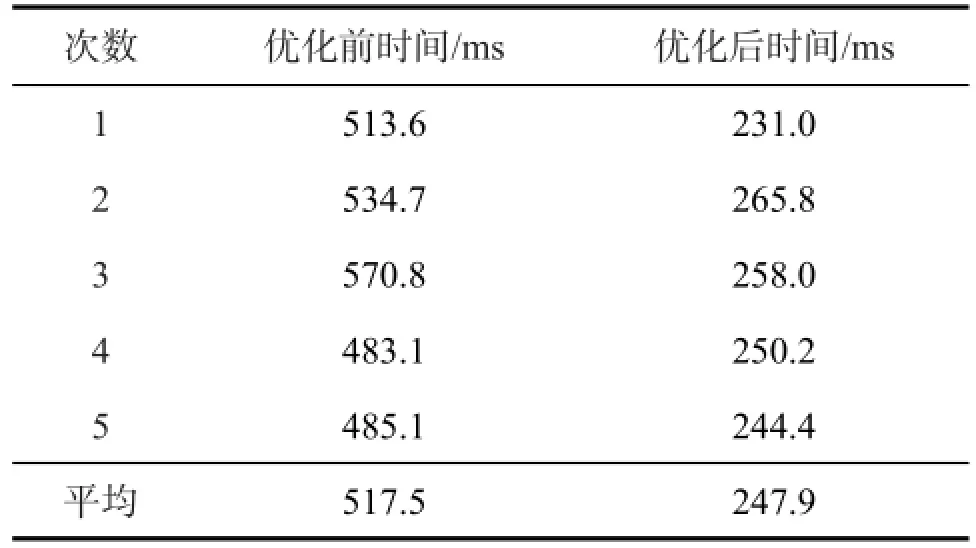
表2 对图5数独问题优化前后求解性能的比较Tab.2 Acomparison of algorithm performance before and after the optimization of sudoku puzzle

从表2可看出，对于图5所示的数独问题，优化后的计算时间比优化前节省了1/2以上，表明提出的问题求解优化算法较简单候选数算法高效。

4 结 论

采用回溯算法建立终盘并基于“挖洞”思想生成有解初盘，提出的“基于大数的回溯算法”可以检测和判断数独初盘是否存在唯一解，该算法应用于对数独初盘产生多解的情况，具备较好的性能。基于求解数独问题的候选数搜索算法，提出1个候选数优化算法，实例分析表明，采用该算法进行数独问题求解明显节约了计算时间。

[1]Garns H.Number place[J].Dell Pencil Puzzles&Word Games,1979,16(5):6.

[2]肖华勇，马丽娜，程海礁.老板数独的方程求解算法研究[J].计算机工程与应用,2014,50(9):41-44.

[3]易珺,朱静文,曹东.数独求解算法的设计与实现[J].科学技术与工程,2010,10(27):6772-6774.

[4]黄皓.数独问题的一种简单解法[J].电脑知识与技术，2014,10(22):5340-5344.

[5]王琼，邹晟.数独问题的求解、评价与生成算法的研究[J].南京师范大学学报：工程技术版,2010,10(1):76-79.

[6]胥剑.回溯法解数独问题[J].电脑编程技巧与维护,2009(5):17-21.

[7]薛源海，蒋彪彬，李永卓.基于“挖洞”思想的数独游戏生成算法[J].数学的实践与认识,2009,39(21):1-7.

[8]Flykinger.数独的候选数法解题技巧(上）[EB/OL].（2009-07-03[2015-02-06]http://blog.sina.com.cn/s/blog_62003b8d 0100mnx4.html）.

[9]程曦，肖华勇，吴林波.数独求解的候选数优化算法设计[J].科学技术与工程,2011,11(26):6409-6412.

[10]姜华林.数独问题高效算法的研究与实现[J].计算机光盘软件与应用,2013,16(219):82-83.

责任编辑：何莉

AStudy of Problem Generation andAlgorithm Optimization of Sudoku Puzzle

HUANG Zuxian
(School of Information Science and Engineering,Central South University,Changsha 410012,China)

Sudoku puzzle includes creating final layout,generating original layout with unique solution,and solving original layout.To create the final layout,an algorithm based on LasVegas and backtrack was proposed,and an original layout with a unique solution was obtained by adopting the idea of digging holes through covering some numbers and combining backtrack algorithm with inverted sequence.In accordance with the division of the original layout into different difficulty groups based on the number of blank blocks there,sudoku puzzle games with different difficulty degrees were created.Furthermore,optimization was also performed in candidates searching algorithm for sudoku puzzle solution.Analysis results of examples show that performance efficiency of the optimized candidate searching algorithm is improved by over 50%,verifying the effectiveness of the proposed algorithm.

sudoku;backtrack;unique solution;candidates;search algorithm

TP312

A

10.3969/j.issn.1671-7872.2015.02.018

2015-03-09

黄祖贤(1993-)，女，安徽马鞍山人，主要研究方向为计算机科学与技术。

1671-7872(2015)-02-0187-05