廉租房保障机制满意度评价研究
常志朋,李 郁,武洪玲
(安徽工业大学商学院,安徽马鞍山243032)
廉租房保障机制满意度评价研究
常志朋,李 郁,武洪玲
(安徽工业大学商学院,安徽马鞍山243032)
为促进并轨后的公租房保障机制能够健康发展,以北京、南京、合肥、长春等城市的4个廉租房小区为例,利用模糊积分综合评价法对廉租房保障机制进行满意度评价。通过入户调查收集保障对象的意见和建议,构建廉租房保障机制满意度评价指标体系。利用单个指标的重视度计算指标集的模糊测度,其中单个指标的重视度采用信息熵计算;最后给出了评价结果及与传统模糊综合评价方法的比较,并根据评价结果给出了廉租房保障机制存在的不足。
廉租房;保障机制;满意度;信息熵;模糊积分综合评价法
廉租房是指政府以租金补贴或实物配租的方式,向符合城镇居民最低生活保障标准且住房困难的家庭提供社会保障性质的住房[1]。我国在1998年提出了建立廉租房的社会保障体系构想,1999年建设部出台《城镇廉租房管理办法》,提出由政府实施住房社会保障职能,向具有城镇常住居民户口的最低收入家庭提供租金相对低廉的普通住房,2014年,我国廉租房和公租房并轨运行,并轨后统称为公租房。对运行15年的廉住房保障机制进行满意度评价,总结该机制存在的优势和不足,不但可以促进公租房保障机制的健康发展,而且还可以加快廉租房和公租房的融合。为此,本文以北京、南京、合肥、长春的4个廉租房小区为例,尝试利用模糊积分综合评价法对廉租房保障机制进行满意度评价。
1 模糊积分综合评价方法
廉租房保障机制满意度评价实质上是一种受到多种模糊因素制约的综合性、主观性评价问题,解决这类问题的传统方法是模糊综合评价法,该方法在处理一些复杂的、难以用精确数学解决的系统问题时,能够表现出很大的优势。但是,应用该方法的前提和基础是评价指标之间彼此相互独立,这就要求在构建评价指标体系时,要严格遵守独立性和全面性原则,以避免指标间存在相关性。对于廉租房保障机制满意度这类主观性评价问题,由于指标的不确定性和专家认识的模糊性,在构建评价指标体系时会不可避免地用多个指标强化评价对象某一方面的重要性,因此很难做到指标间彼此独立,往往会存在一定的相关性或交互作用,如果在评价过程中,指标间相关性或交互作用不予考虑,可能会导致评价结果失真。为此,本文采用基于模糊测度[2]和模糊积分算子[3]的模糊积分综合评价法[4]来处理指标间存在的相关性或交互作用。
模糊测度是由日本学者Sugeno用比较弱的单调性代替可加性定义的一类集函数[5]。模糊测度是可以将指标间的相关性或交互作用列入考虑的主观计量模糊对象的尺度[6]。
定义1[7]设为有限集,(X,P(X))是一可测空间,是一组函数,具有如下性质:
(1)g(∅)=0,g(X)=1;
(2)∀A,B∈P(X),若A⊆B,则有g(A)≤g(B);
函数g称为模糊测度,如果还满足以下条件:对于∀A,B∈P(X),A⋂B=∅,存在λ>-1使得
则称g为λ模糊测度。式中λ值可以通过下式唯一确定,即
令gi=g(Xi)为评估者对评价指标Xi的重视度,如果,则
模糊积分是定义在模糊测度基础上的一种非线性集成算子,它不需要假设指标间相互独立,因此广泛被应用于指标间具有相关性或交互作用的主观评价问题。模糊积分的形式较多,常用的有Sugeno积分和Choquet积分,本文采用Choquet积分。
定义2[8]设集函数g:P(X)→[0,1]为可测空间(X,P(X))上的模糊测度,μ:X→[0,1]为X上的非负实值可测函数,则μ关于g的Choquet积分为
基于传统模糊综合评价原理[9],可以利用模糊测度和模糊积分算子构建如下方法对廉租房保障机制满意度进行评价[4]:
2 廉租房保障机制满意度评价
2.1 构建评价指标体系
能否对廉租房保障机制满意度进行有效评价,关键是构建一套能够全面测度廉租房保障机制,并且能够被保障对象认可的评价指标体系。因此,课题组以北京、南京、合肥、长春的4个廉租房小区(表1)为例,广泛调研保障对象对廉租房保障机制的意见和建议,进而构建廉租房保障机制满意度评价指标体系。调研采取随机入户的方式,每小区发放80份问卷,共发放问卷320份,有效问卷304份,有效率为95%。

表1 廉租房小区Tab.1 Low--rent--house communities
本次调研共收集整理了廉租房保障机制存在的7类问题:
(1)在调研中发现有47.10%的保障对象认为“管理人员对自己的实际困难并不了解,很难和管理人员建立有效的沟通渠道”,特别是家中有老人和小孩的保障对象认为,虽然收入逐年有所提高,但是随着夫妻双方父母年纪逐渐增大,在疾病治疗方面的支出也逐年增多,另外还有子女在教育、衣食方面的开支也在逐年增加,希望政府能充分考虑他们的实际情况,提高退出的收入标准;
(2)有68.40%的个体经营者认为“收入认定不合理”,认为虽然他们有营业执照、有车,但都是经营的必要手段,并不能代表他们收入很高,特别是大部分家庭的车都是经营性用车;
(3)部分地区的保障对象认为“退出标准设定的不合理”,在调查中发现一些保障家庭认为“人均住房面积超出规定的住房保障标准”这一条很不合理,保障房的人均面积同家庭收入并没有必然联系;
(4)有38.50%的保障对象对具体满足什么条件要从保障房中退出并不是很了解,可见廉租房的退出政策宣传、讲解的力度还远远不够,特别针对一些低收入、低学历的困难群体要在宣传的方法上有所创新;
(5)有71.28%的保障家庭反映所在小区存在不符合规定的保障对象居住在廉租房小区,这也表明“准入”的公平与否直接关系到“退出”的公平与否;
(6)一些保障对象反映,对于具体哪些保障对象“不需要退出”应该公示,接受社会监督,但是对于“需要退出”的也应该提前公示,广泛征询意见;
(7)有56%保障对象对保护个人隐私方面不是很满意,他们认为在接受社会监督、政府入户调查、社区审核的同时也应该保护其个人隐私;
通过上述分析,课题组经过反复讨论并征询领域专家的意见,构建了图1所示的廉租房保障机制满意度评价指标体系。
2.2 利用信息熵计算单个指标的重视度
熵是简单巨系统的基本概念,代表着系统的混乱程度或无序程度。信息论中,信息熵是不确定性在数量上的度量[10]。对于一个系统,系统越有序,信息熵就越低;反之,信息熵就越高。在多指标综合评价系统中,如果评价指标的熵越小,就表明其指标值的变异程度越大,决策者越应该重视该指标的作用[11]。本文利用信息熵来测度单个指标的重视度,具体方法如下。
邀请5位专家,记为S={St|t=1,2,3,4,5},根据每位专家的知识和经验设定专家权重向量,记为令为专家St对二级指标Xij的重视度打分,打分尺度可以参照表2。

表2 指标重视度的打分尺度Tab.2 Density scale of single index
5位专家对指标X1={X11,X12,X13},X2={X21,X22,X23,X24}和X3={X31,X32,X33,X34}的重视度打分矩阵分别为

表3 二级指标的信息熵Tab.3 Information entropy of second-level indexes
由于指标Xij的信息熵值eij越小,指标Xij同其他指标间的差异越大,该指标越应该重视,因此可以用gij=1-eij计算指标Xij的重视度,具体数值见表4。

表4 二级指标的重视度Tab.4 Density of second-level indexes
根据表4中的数据,同理可以计算一级指标Xi的信息熵值,见表5。故可得一级指标Xi的重视度:

表5 一级指标的信息熵值Tab.5 Information entropy of first-level indexes
2.3 计算指标集可测空间上的模糊测度
2.4 计算二级指标的模糊评价矩阵
二级指标的评价数据主要通过在小区内以随机问卷的方式获取,要求被访问者对指标{X11,X12,X13,X21,X22,X23,X24,X31,X32,X33,X34}进行评价,指标的评语集设定为“满意(θ1)”、“一般(θ2)”、“不满意(θ3)”、“很不满意(θ4)”4个等级,共发放270份问卷,有效问卷242份,有效率90%,见表7。

表6 模糊测度值Tab.6 Fuzzy measure values

表7 调研问卷Tab.7 Investigation questionnaires
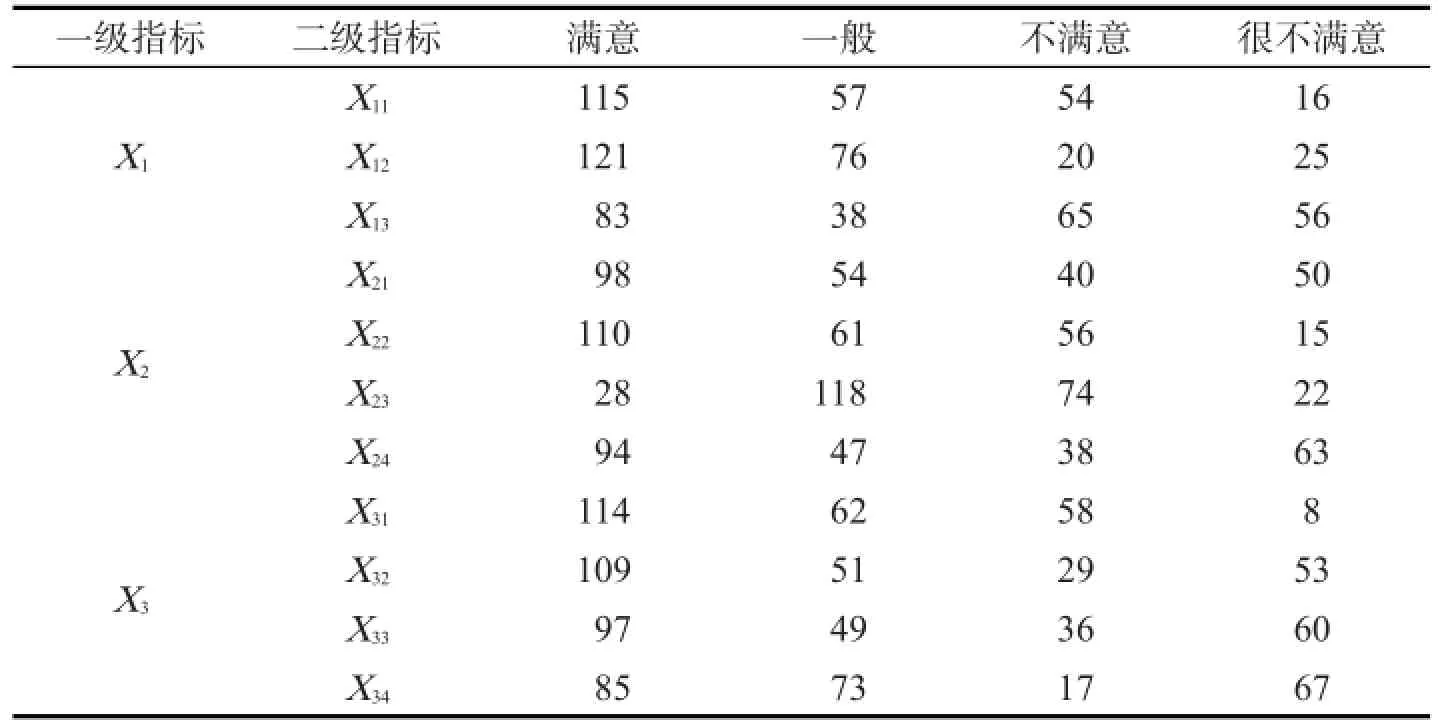
表8 指标评语Tab.8 Fuzzy remarks of indexes
表8为评语的统计表,根据表8计算二级指标的模糊评价矩阵如下:
2.5 计算一级指标的模糊评价矩阵
利用式(8)计算一级X1指标的模糊评语值
然后利用(9)进行归一化,得指标X1的模糊评语向量为
同理,计算指标X2和X3的模糊评语向量分别为
根据B1,B2和B3得到指标X1,X2和X3的模糊评价矩阵为
2.6 评价结果分析及比较
根据模糊评价矩阵R,本次调研的廉租房保障机制满意度评价向量为
根据B可知,总体上廉租房保障机制是令人满意的,对目前运行的“准入机制(X1)”、“公开机制(X2)”和“退出机制(X3)”基本满意。但是也存在一些问题,如“投诉、举报渠道的畅通性(X23)”满意度较低,“配租程序的公开、公正、公平性(X13)”和“应退尽退”情况(X31)”满意度不高。在今后的公租房保障机制建设中,政府还需要强化投诉渠道的畅通性,提升社会监督的力度,同时还要保证准入、退出的公平性。
本文所采用的满意度评价工具是模糊积分综合评价法,该方法能够很好的考虑指标间存在的相关性或交互作用,使决策结果更符合实际,为验证本方法的优越性,本文与传统的模糊综合评价法进行对比分析。为了保证两种方法具有可比性,传统模糊综合评价法指标权重的计算采用表3和表5的信息熵值。二级指标的权重采用计算,一级指标的权重采用计算,具体计算结果如下。

表9 各级指标权重Tab.9 Weights of every level index
根据模糊评价矩阵R1,R2和R3,计算一级指标的模糊评价矩阵为
最后,计算得到模糊评价向量为B′=(0.398 1,0.257 0,0.182 8,0.162 2)。从模糊评价向量B和B′看,两种方法的评价结果一致,都为“满意”,但是本文方法“满意”的置信度更高,结果更可靠。
3 结 语
以北京、南京、合肥、长春的4个廉租房小区为调研对象,构建了廉租房保障机制满意度评价指标体系,并在此基础上收集了相关的评价数据。为避免指标间相关性对评价结果的影响,采用模糊积分综合评价法对廉租房保障机制满意度进行了评价,评价结果表明廉租房保障机制基本令人满意。
[1]龙灏.城市最低收入阶层居住问题研究—重庆市廉租房体制及其选址与设计探析[M].北京:中国建筑工业出版社,2010: 114-120.
[2]Sugeno M.Theory of fuzzy integral and its applications[D].Tokyo:Tokyo Institute of Technology,1974.
[3]Ishii K,Sugeno M.A model human evaluation proeess using fuzzy measure[J].International Journal of Man-machine Studies, 1985(22):19-38.
[4]常志朋,程龙生.基于模糊积分综合评价法的我国应急物资对外采购能力评价[J].中国安全生产科学技术,2012,8(9): 106-111.
[5]王熙照.模糊测度和模糊积分及在分类技术中的应用[M].北京:科学出版社,2008:14-15.
[6]朱传军,卢新海,韩长生.基于模糊积分的开发区土地经济效益评价[J].中国土地科学,2009,23(5):53-58.
[7]Sugeno M.Fuzzy Measure and Fuzzy Integrals,a Survey,Fuzzy Automata and Decision Processes[M].New York:North-Holland,1997:89-102.
[8]Murofushi T,Sugeno M.A theory of fuzzy measures,representations,the choquet integral,and null sets[J].Journal of Mathemati calAnalysisAndApplications,1991,159(2):532-549.
[9]杨纶标,高英仪.模糊数学原理及应用[M].广州:华南理工大学,2005:80-88.
[10]曾佳龙,黄锐,关燕鹤,等.熵权-未确知测度理论在尾矿库安全标准化中的应用研究[J].中国安全生产科学技术,2014,10(2):160-166.
[11]赖芨宇,张晋,刘菁,等.信息熵的模糊选择在项目管理组织结构中的应用[J].武汉工程大学学报,2014,36(3):67-71.
责任编辑:丁吉海
Satisfaction Evaluation of Low-rent Housing Safeguard Mechanism
CHANG Zhipeng,LI Yu,WU Hongling
(School of Business,Anhui University of Technology,Ma'anshan 243032,China)
After low-rent housing was incorporated into public rental housing,to promote healthy development of new public rental housing,four low-rent housing communities in Beijing,Nanjing,Hefei and Changchun respectively are taken as an example to evaluate the satisfaction of low-rent housing safeguard mechanism.The satisfaction is evaluated by fuzzy integral comprehensive evaluation method(FICE).The evaluation index system of lowrent housing safeguard mechanism is established according to the opinions and suggestions of guarantee.To calculate the fuzzy measure,the information entropy is used to calculate the density of single index.Finally,the evaluation results and the comparisons of FICE and fuzzy comprehensive evaluation method(FCE)are given.Besides, according to the evaluation results of FICE,the disadvantage of low-rent housing safeguard mechanism is given.
low-rent housing;safeguard mechanism;satisfaction;information entropy;fuzzy integral evaluation method
F293.33
A
10.3969/j.issn.1671-7872.2015.02.019
2014-06-15
国家自然科学青年基金(71303004);教育部人文社会科学青年基金(12YJK630005);安徽省哲学社会科学规划基金(AHSK11-12D73)
常志朋(1978-),男,吉林榆树人,博士,副教授,主要研究方向为管理综合评价、多属性决策。
1671-7872(2015)-02-0192-08

