基于时变市场分数的状态依赖自信的金融市场动态模型
王 婧
(伊犁师范学院数学与统计学院,新疆伊宁835000)
近年来,由异质交易者关系引起的金融市场价格动态模型文献得到了较好的发展,如Hommes[1]等.一方面,这些文献说明异质交易者如何相互影响,并产生偏离基准价格的持续价格偏差;另一方面,模型能够说明经典的收益时间序列及分布的特征,这些特征的出现与非线性因素密切相关.其中,基本面分析者-技术分析者关系模型扮演特定的角色,能够捕捉基本的价格波动机制.从数学观点看,在强趋势推断下阻止价格发散是一些非线性调整机制.Day and Huang[2]分析指出,非线性因素与基本面分析者关于资本损益的已知机会相关.由Brock and Hommers[3]提出的相关模型,之后由Chiarella and He[4-5]作了更进一步的研究,即代理商依据基于已知收益的非线性机制在消费理性与不理性预计法则之间转变.遵循同样的观点,本文根据Chiarella et al.[6]研究提出,基本面分析者由于具有稳定市场的力量,随着价格偏差变大也最终会带动价格回馈到基准价格.
我们考虑具有两种异质交易者的金融动态模型,即基本面分析者与技术分析者.技术分析者采用GDP过程形成期望,而非简单的AR(1)过程,因为AR(1)过程在实证分析当中缺乏收益的自相关性.Chiarella et al.[7]研究中的技术分析者采用GDP过程,并引入噪声交易者,用S&P数据进行实证分析,得到了很好的金融市场典型的程式化事实:尖峰厚尾以及波动聚集性,而基本面交易者被假定是通过良好的经济环境来形成期望,然而预测的自信度是状态相依的,价格偏离基准价格较大,其更倾向于回馈到基准价格,同时,我们考虑市场分数的变化,Dieci et al.[8]采用时变的市场分数,考虑了市场情绪与发展适应性.这是对He[9](考虑了市场分数的情形,即MF模型,被用来解释金融市场行为的各个方面,并建立随机模型和其潜在的确定性系统之间的联系)的发展延伸.
1 建立模型
根据 Chiarella et al.[6]的模型
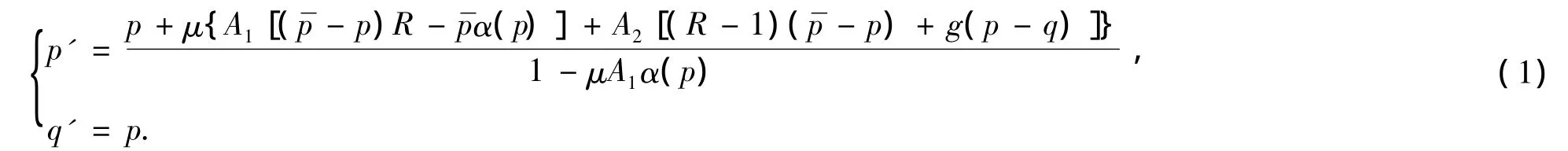
这里假定有两类投资者,即基本面分析者和技术分析者,分别用类型1和类型2表示.但我们引入时变的市场分数,根据Dieci et al.[10]分别令q1,t,q2,t为投资者的市场分数.假定市场分数为固定部分和时变部分.在t 时的市场分数(q1,t,q2,t)表达为
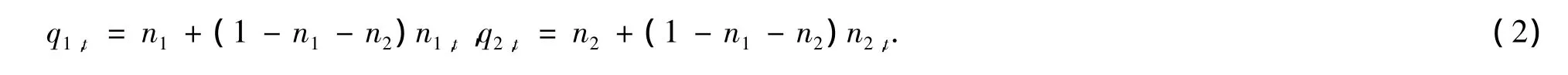
其中,n1和n2=1-n1表示基本面分析者和技术分析者在时间t的“不改变”投资者的比例.n1,t和n2,t表示时间 t的时变投资者比例.令 n0=n1+n2,m0=(n1-n2)/n0,mt=n1,t-n2,t.
那么市场分数又可重新写为
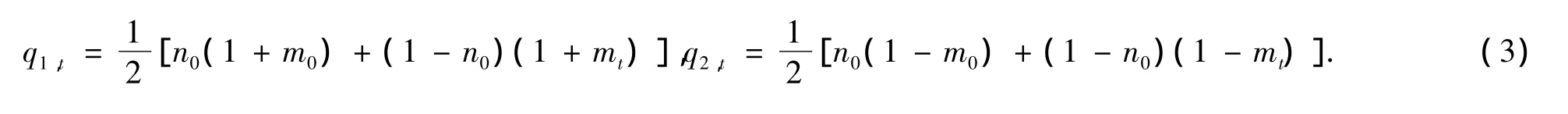
1.1 异质期望
下面分析其本面分析者和技术分析者是如何采用不同的机制形成未来价格的预期.这里基本面分析者采用相同的价格预期.对于技术分析者来说,技术分析者一方面考虑过去的价格及价格的改变,另一方面他们用移动平均法则,通过比较短期移动平均和长期移动平均形成期望,对移动平均过程加入一个套利滞后长度,所以使用几何衰减过程(GDP).这样技术分析者的期望可以写为
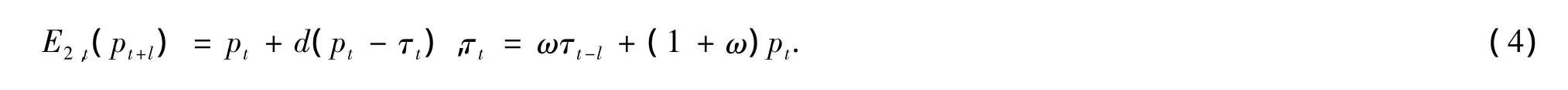
其中,τt为几何衰减函数,ω∈[0,1]为记忆衰减率.ω越大,过去的价格对目前的趋势影响越大.d代表推断强度.如果d≥0则称技术分析者为追风者,若d<0则称其为逆风者.
1.2 动力系统
利用以上分析,基本面分析者和技术分析者的需求函数可以写为
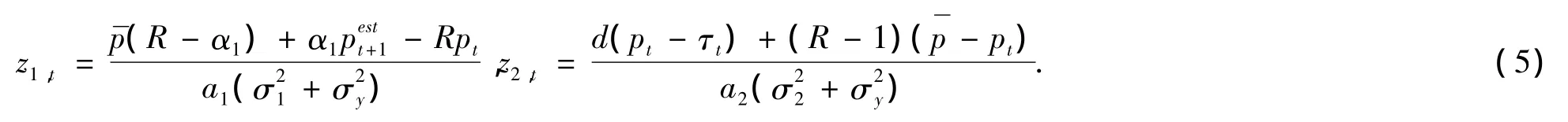
其中,πh,t+1为两类投资者从 t到 t+1 时期的已知收益,πh,t+1=zh,t(pt+1+yt+1-Rpt),h=1,2.
遵循Brock and Hommes[3][11]的方法,假定时变投资者的比例由离散选择模型决定,有

其中,Ch≥0是策略的固定成本,而参数β是选择强度用来测度适应性理性交易者的比例对最优策略的敏感度.记 mt+1=n1,t+1-n2,t+1,那么此时价格制定为
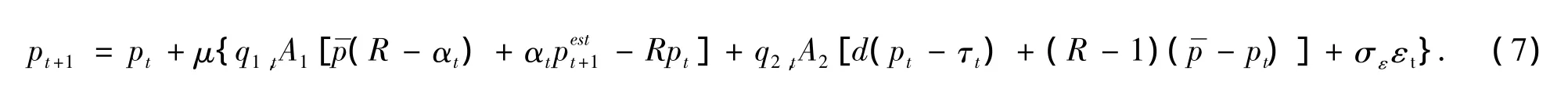
这里令 A1=1/(a1[+]),A2=1/(a2[+]).
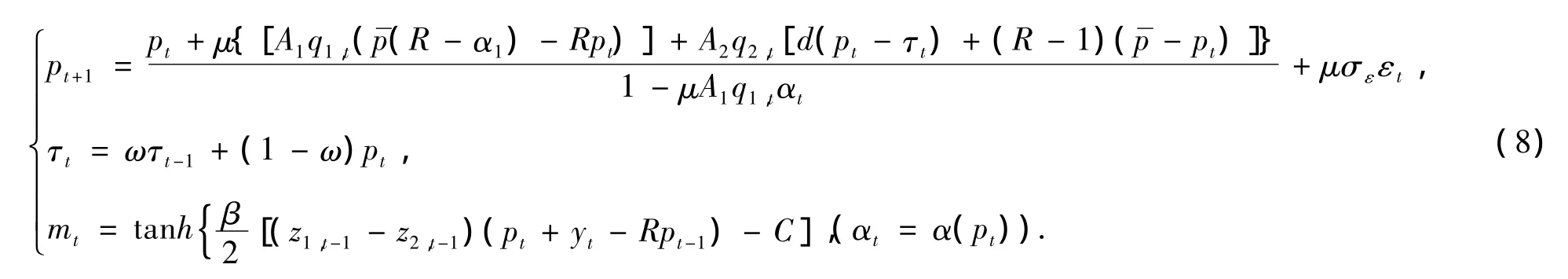
以下的动力学分析是通过假定σε=0来做的,得到了所谓的确定性动力系统模型.
2 映射及其特性
3维确定性动力系统由3维映射 T:(p,τ,m)→(p',τ',m')给出:
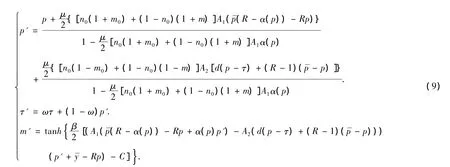
现在,简要地讨论一下平衡点的稳定性、稳定性区域及分支情况.概括为如下定理.
定理2 (i)若ω =0,当0<μ<μ*时,基本平衡点是稳定的,这里=[n0(1+m0)+(1-n0)(1+]/2=[n0(1-m0)+(1-n0)(1-]/2.另外,在μ = μ*处产生Flip分支.(ii)若0<ω<1,由参数(d,μ)确定的区域Ω为平衡状态的局部渐近稳定区域,Ω =ΩF∪ΩN,这里 ΩF={(d,μ):d≤d0,0<μ<μF(d)},ΩN={(d,μ):d > d0,0<μ<μN(d)},且当d≤d0时,在 μ=μF(d)的边界上产生Flip分支,当d>d0时,在μ=μN(d)的边界上产生Hopf分支.其中
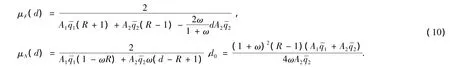
证明在平衡点处的特征方程为λΓ(λ)=λ[λ2-(A+ω+(1-w)B)λ+Aω]=0.其中A=知0是特征根,其它两个特征根满足Γ(λ)=λ2-(A+ω+(1-ω)B)λ +Aω =0.
当ω =0时,Γ(λ)=λ[λ-(A+B)],基本平衡点稳定只需满足-1<λ =A+B <1,即0<μ <,且当λ =A+B=-1时,即μ=μ*时产生Flip分支.
当0<ω<1时,由Jury判据知,特征根在单位圆内,即基本平衡点是稳定的,需满足以下条件:(i)Γ(1)> 0;(ii)Γ(-1)> 0;(iii)ωA<1.
上述式子成立需1-μA1>0,则(i)Γ(1)>0恒成立;(ii)Γ(-1)>0等价于d≥d1或d<d1,0<μ< μF(d),其中(iii)ωA <1等价于d≤d2或d>d2,0 <μ <μN(d),其中
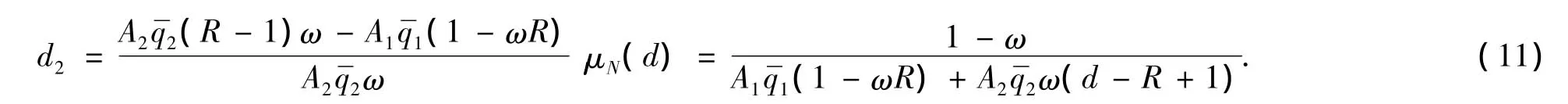
当μF(d)= μN(d)时解得d0,有d2<d0< d1,而
因此,稳定性条件就降为:当d≤d0时,0<μ<μF(d);当d>d0时,0<μ<μN(d).
另外,当μ = μF(d)时,Γ(λ)=0的两个特征根满足λ1=-1以及λ2∈(-1,1);当μ = μN(d)时满足|λ1,2|<1.因此当d≤d0时,在μ=μF(d)边界上发生Flip分支;当d>d0时,在μ=μN(d)边界上发生Hopf分支.
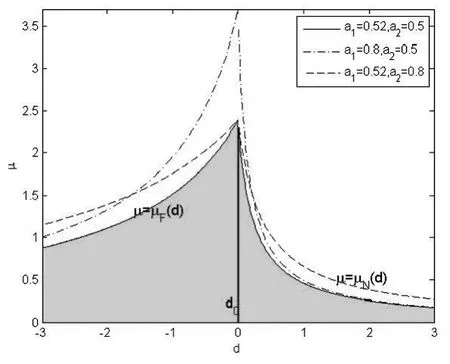
图1 (d,μ)平面上稳定区域示意图
图1画出了(d,μ)平面上的稳定区域,从分支边界表达式易得出不同的参数对稳定区域的影响.即参数在一定范围时,增大,β,a1,a2,减小 m0,n0,ω,C,可以使稳定区域增大,反之亦然.
3 结语
本文研究了在简单的做市商定价机制下含两类异质期望投资者,即基本面分析者与技术分析者,并加入了时变的市场分数的三维离散时间资产价格动力学模型.所不同的特点是假定基本面交易者拥有经济环境的良好信息(包括技术分析者的信念),并以此形成将来价格的期望,而且当价格偏离基准价格变大时,他们会置更过的权重于均值回馈到基准价格.这个机制能够保证当基本平衡点局部不稳定时模型的全局稳定性,以此避免价格的发散.并在讨论确定性系统时,得到了相应的分支边界以及不同参数对稳定区域的影响.
[1]Hommes C H.Heterogeneous agent models in ecnomics and finance[J].Handbook of computational economics,2006(2):1109-1186.
[2]Day R H,Huang W.Bulls,bears and market sheep[J].Journal of Economic Behavior & Organization,1990,14(3):299-329.
[3]Brock ,W.,Hommes C.H.Heterogeneous beliefs and routes to chaos in a simple asset prcing Model[J].Journal of Economic Dynamic & Control,1998(22):1235-1274.
[4]Chiarella C,He X Z.Heterogeneous beliefs,risk and learning in a simple asset pricing model[J].Computational Ecnomics,2002,19(1):95-132.
[5]Chiarella C,He X Z.Heterogeneous beliefs,risk,and learning in a simple asset- pricing model with a market maker[J].Macroeconomic Dynamics,2003,7(4):503-536.
[6]Chiarella C,Dieci R,Gardini L,et al.A model of financial market dynamics with heterogeneous beliefs and state-dependent confidence[J].Computional Economics,2008,32(1-2):55-72.
[7]Chiarella C,He X Z T,Zwinkels R.Heterogeneous expections in asset pricing:Empirical evidence from the S&P 500[J].Journal of economic behavior& organization,2009(105):1-16.
[8]Dieci R,Foroni I,Gardini L,et al.Market mood,adaptivebeliefs and asset price dynamics[J].Chaos,Solitons&Fractals,2006,29(3):520-534.
[9]He X.Asset pricing,volatility and market behavior:a market fraction approach[M].Sydney:School of Finance and Economics,University of Technology,2003.
[10]Chiarella C,Dieci R,He X Z.Heterogeneous expectations and speculative behavior in a dyn-amic multi- asset framework[J].Journal of EconomicBehavior & Organization,2007(62):408-427.
[11]Brock ,W & Hommes C.H.A rational route to randomness[J].Econometrica,1997(65):1059-1095.
[12]王联,王暮秋.常差分方程[M].乌鲁木齐:新疆大学出版社,1991:202-204.

