OTC金融衍生品测控模型的构建与压力测试

聂亦慧

（西安石油大学经济管理学院，西安 710054）

0 引言

场外交易金融衍生品（简称OTC金融衍生品）通常是指在交易所以外或柜台交易的金融衍生品，由交易双方根据各自需求协商完成。目前，在国内OTC金融衍生品市场上，主要有远期、期货、互换、期权四种基础产品，其他的结构性产品是从这四种基础产品衍生而来。由于OTC金融衍生品属于结构性产品，其定价受到市场利率的影响，因此在实施过程中，金融机构需要根据市场利率的变化对其风险进行监控。何树红（2010）、杨晋渝（2012）等人研究得出OTC金融产品具有明显非线性特征，而其他资产的价值变化通常具有显性特征。张玉红、冯宗宪（2009）、周件（2010）等人研究得出经典B-S定价模型的前提条件假设要求高，不再适合OTC金融衍生品的定价。陈锦磊（2013）研究得出，对于OTC金融衍生品市场监控，市场本身的内部调节机制难以发挥作用，需加强OTC衍生品市场内部控制。潘慧峰（2013）研究发现随机过程设定会导致OTC金融衍生品定价风险，风险会随着随机过程与估计样本的变化而变化，衍生品买卖双方的模型风险呈现非对称性特征。由于金融产品的风险管理是一个过程管理，为了在产品执行过程中对风险进行有效监控，论文构建考虑信用状况与市场利率复合影响的复合因子监控模型，并利用蒙特卡罗仿真方法对OTC金融衍生品监控模型进行了压力测试。

1 OTC测控模型的构建与敏感性分析

1.1 变量选取与模型的构建

本文以某商业银行OTC金融衍生品为标的，数据来源于该商业银行与外资银行共同经营的案例，选取254个样本。以收益利差(Spread=Yield-Libor)作为被解释变量，期限（T）、市场利率（Libor）、信用评级(Rank)、期限与信用评级的乘积(TRank)、信用评级与市场利率乘积（RankLibor）、期限与市场利率的乘积(TLibor)、以及三者的乘积（TRankLibor）7个变量作为解释变量，考虑到结息期对收益利差的影响，同时引入哑元（SD）变量。为了清楚地反映问题，市场利率选自伦敦同业拆借市场7天Libor，利用样本年收益率Yield与Libor两者之差作为收益利差。将简单因子和复合因子代入监控模型，进行多元逐步线性回归，从中检验复合模型的影响因素，得到以下假设模型：

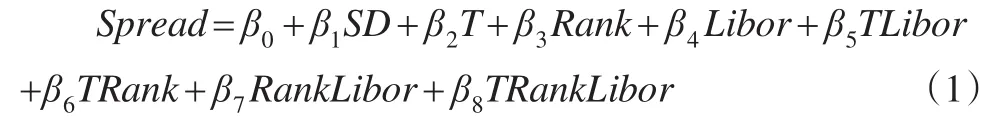
使用SAS统计软件，经过4步迭代终止，从表1可看出方程的显著性F检验比较显著；R方回归的拟合度较好。

从表2可以观察发现模型的VIF均小于10，而且在95%的置信度下，F检验和t检验均显著，说明模型4比较理想。于是得出如下监控模型：

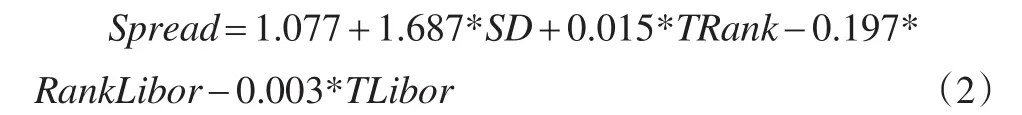
1.2 敏感性分析

依据表2数据，本文有如下结论：

（1）SD是定序变量，它是用来区分产品的类别的，产品选定后，SD是确定的。

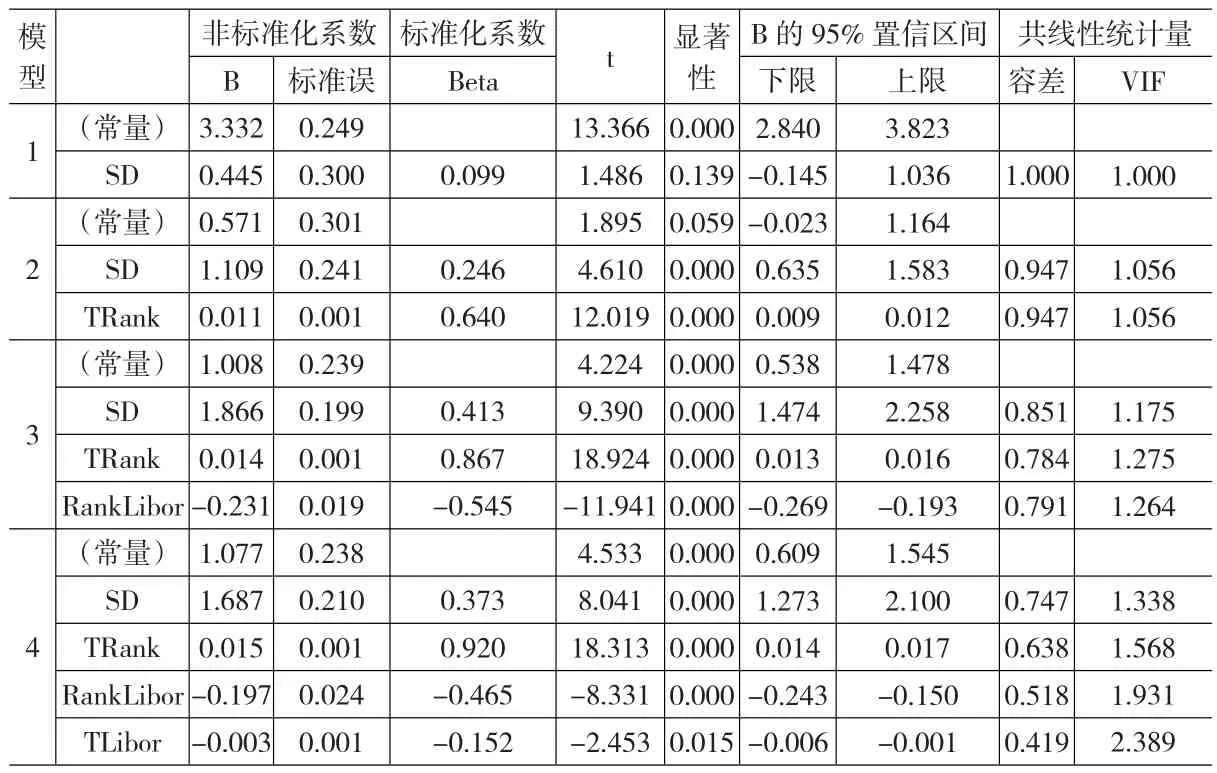
表2 系数估计

（2）T和Rank控制不变，Libor增加一个单位，收益利差Spread减少(0.197*Rank+0.003T)个单位；T和Rank控制不变，Libor减少一个单位，收益利差Spread增加(0.197*Rank+0.003T)个单位；当市场利率发生变化时，收益利差Spread将受到影响，呈反向变化。

（3）T和Libor控制不变，Rank增加一个单位时，当Libor小于0.0761T（0.015/0.197）时，收益利差 Spread增加（0.015T-0.197Libor）个单位，否则收益利差Spread将减少（0.015T-0.197Libor）个单位，也就是说期限与Libor的组合会影响到产品的信用风险。

（4）Rank和Libor控制不变，T增加一个单位时，当Libor小于5Rank（0.015/0.003）时，Spread增加（0.015Rank-0.0 03Libor）个单位，否则Spread将减少（0.015Rank-0.003Libor）个单位，评级最小为1，所以通常Libor会小于5Rank，于是期限延长，收益利差会增加。

从表2可发现同期限的产品，收益率随着基准利率和信用等级的变动而变动的情况。当产品的收益利差小于0时，产品不再有利可图，所以产品面临提前终止的风险。

2 测控模型的压力测试

OTC金融衍生品的风险管理是一个过程管理，金融产品在实施过程中，须根据市场利率的变化对其风险进行监控。由于OTC金融衍生品是新型金融衍生产品，市场相对狭小，信息披露也有限，这类产品主要涉及美元产品，因此，本文采用由相应期限的伦敦同业拆借市场利率Libor来作为OTC金融衍生品的市场价格，测控OTC金融衍生品的风险。

2.1 蒙特卡罗模拟

本文假定，在当前的无风险利率水平下，r0是无风险利率，M为均值回复水平；a为回复速率；σ为波动率。文中采用均值回复的利率过程来模拟七天后的Libor，根据相关研究，参数r0、M、a、σ不妨分别取5.30%、6%、0.048、0.0007。蒙特卡罗模拟方法对扩展的定价模型求解的过程的步骤具体如下：

（1）随机方程离散化。

将CIR模型离散化：

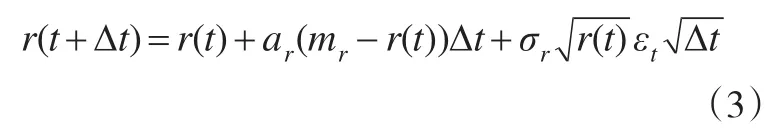
其中，εt为标准正态分布中所抽取的随机数。

（2）模拟利率的路径。

根据离散化形式模拟出利率过程的路径。首先，将利率的期限分割成N期，每期时间步长皆为Δt(=T/N)；之后，从标准正态分布中抽出N个独立的随机数，依据设定的初始值和公式（3）计算出r(ti)，ti=ti-1+Δt，即可得到在时点0，t1，t2，…，T的利率，由此产生一条利率的路径。重复M次模拟试行之后，可以得到M条利率的路径。

（3）计算出给定置信度下的利率的VaR。

经过排序，选定置信度，就可以得到利率的VaR。

根据前面提供的参数，应用蒙特卡罗模拟方法模拟7天Libor，模拟10000条径路。模拟路径如图1所示。

图1 蒙特卡罗模拟路径图

图2 蒙特卡罗模拟七天的利率直方图

从图2可以看出，7天的利率很好的拟合了正态分布。而且1天一直到7天的模拟利率都通过了99%的Kolmogorov-Smirnov正态分布检验。

2.2 压力测试结果分析

商业银行通常在95%～99%之间取置信度的值，依据BASEL的要求取值99%，又依据RBS（苏格兰皇家银行）的经验取值为97.5%，同时取下限值95%。故此，分别取三种不同的置信度99%、97.5%、95%，对应的VaR分别取0.0559，0.0558，0.0557。由于限于篇幅，本文只给出VaR在99%和97.5%置信度下的收益利差，对于95%置信度下的收益利差不再给出，只给出相应收益利差与信用等级和产品期限的关系。

VaR压力测试通常是假定市场出现最不利的情况下，银行面临的最大损失。以上表3、表4（表5没有给出）可以发现，在相同置信度下，随着期限延长，收益利差变小；在相同的期限下，除信用1级(AA+信用等级最高)外，随着信用等级的降低，收益利差变大。同时从表中也可以发现，对于信用1级(AA+信用等级最高)来说，基本上没有信用风险，市场利率影响长期收益要比短期收益大些，收益利差随期限延长而变小，这与现实情况相吻合。从信用2级（AA）开始，受市场利率和期限的共同影响，信用利差变化较大。通常随着信用等级的增大对收益率的要求也较高，收益利差也较大。论文通过VaR方法量化OTC金融衍生品的风险，为商业银行OTC金融风险管理提供了量化手段。

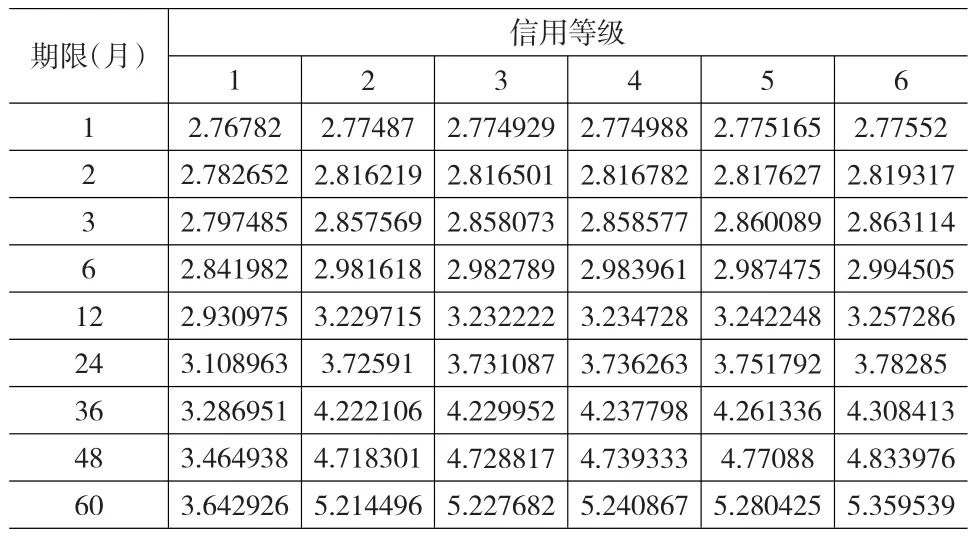
表3 VaR在99%置信度下的收益利差

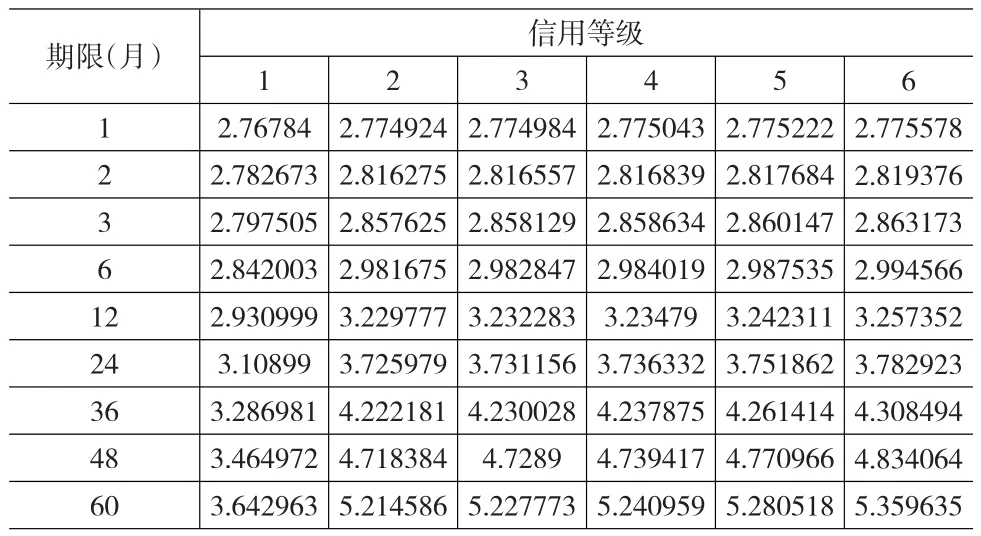
表4 VaR在97.5%置信度下的收益利差

3 结论

本文构建了OTC金融衍生品的复合因子监控模型。通过收益利差对产品期限、市场利率和信用等级等进行逐步线性回归，建立了OTC金融衍生品复合因子的监控模型；受产品期限、市场利率和信用状况的影响，收益利差呈非线性变化，主要原因是信用状况与产品期限、市场利率三者存在相互影响。另外，本文借鉴VaR思想，利用蒙特卡罗模拟方法对监控模型进行模拟，对OTC金融衍生品收益进行了压力测试。考虑在极端情况下，市场利率的变化引起收益利差的影响，这些相关影响因素是产品定价事前控制的主要内容。

根据以上分析，本文对我国商业银行OTC金融衍生品风险管理提出如下建议：

（1）重视风险因素的相关性，提高风险识别的有效性。场外金融衍生产品的特性是市场风险与信用风险具有相关性。目前我国商业银行主要通过外资银行和境外的市场进行金融衍生品的交易，尚未真正自主进行产品的设计和定价。因此在进行产品开发时，对各种资产组合中的分布建立模型时，须考虑风险因子的相关性，事前识别市场上未预测到的因素和极端的交易条件带来意想不到的相关性，从而降低模型的失效性，提高风险识别的有效性。

（2）强化产品定价的复合因素，规避风险因素。从基本的金融理论出发，须运用OTC金融衍生品复合因子定价模型来进行产品定价。基准利率是产品定价时事前参考的利率,当市场利率发生变化时，产品的收益率将受到影响，呈反向变化。产品期限与收益率呈相同方向变化，期限长要求的收益率就高，当期限比较长时，信用等级的增加会显著影响结构产品的定价，长期的产品相对信用风险比较大，信用利差比较高；短期内结构化产品的信用风险相对比较小，信用利差也比较小。由于期限和利率，收益率与信用等级呈非线性关系，信用等级本身与期限相关，基准利率变化又会影响信用等级。故OTC金融衍生品的利率产品须运用复合因子定价模型来进行产品定价。

（3）实施风险监控，进行风险动态管理。金融产品的风险管理是面向过程管理，为了在产品执行过程中对风险进行监控，充分考虑信用状况与市场利率复合影响的监控模型，对商业银行OTC金融衍生品的管理进行事中监督，从而实时控制风险，避免发生违约风险。

[1]Manmohan S.Collateral,Netting and Systemic Risk in the OTC Derivatives Market[Z].Working Papers from International Monetary Fund,2010.

[2]Ingves S.Regulatory Reforms for OTC Derivatives:Past,Present and Future[J].Financial Stability Review,2013,（7）.

[3]杨晋渝.基于最谨慎原则的信用衍生品定价模型及应用[J].数量经济技术经济研究，2012,（10）.

[4]何树红，高彩云.商业银行金融衍生业务的风险控制[J].金融理论与实践，2010,（5）.

[5]熊玉莲.我国场外金融衍生品交易商监管：路径选择与制度完善[J].上海经济研究，2012,（2）.

[6]王娟.金融衍生品定价模型及二阶段运算[J].统计与决策，2011,（22）.

[7]周件.金融衍生品的定价与过度需求——对中国企业介入金融衍生品的一个理论解释[J].中央财经大学学报，2010,（10）.

[8]张玉红，霍天翔，冯宗宪.OTC金融衍生品交易市场的发展探析[J].上海金融，2009,（8）.

[9]陈锦磊.基于博弈论的OTC金融衍生品市场监管必要性分析[J].商业经济，2013,（9）.

[10]潘慧峰.复杂衍生品定价的模型风险度量——以中信泰富杠杆式外汇合约为例[J].中国软科学，2013,（8）.