商贸流通产业发展与城市化进程关系实证分析

■ 王国锋 副教授 刘小娟 博士 邱 虹 博士生（1、北京大学光华管理学院 北京 1008712、电子科技大学经济与管理学院成都 61171、重庆市对外经济贸易委员会 重庆 00020、西南财经大学统计学院 成都 61171）

长三角地区城市化与流通业发展

（一）长三角地区城市化水平

1.总体水平。总体来看，长江三角洲地区是我国城市化水平最高的区域，且与全国的平均城市化水平正在逐渐拉大。长三角地区的城市化发展过程为：1990-1999年，是平稳发展阶段；2000-2006年是高速发展阶段；2006年以后，长江三角洲的城市化进入瓶颈期。尤其是近年来，部分二线城市脱离区域发展状况，盲目追求速度，一定程度上造成了区域城市体系的失调。因此在此背景下，研究城市化水平与商贸流通业的动态关系，对指导我国的城市化健康发展具有重要的现实意义。

2.各省市的城市化发展状况。从1990年代开始，上海的城市化率就一直领先于江苏、浙江两省，并能早在2004年，上海的城市化水平已达到发达国家水平，每年的城市化环比增长速度约为3.3%。20世纪90年代是浙江省城市化的大力发展起始阶段，浙江省主要依靠自主经商为主动力，在大城市周边建立一批中小城市，完善和提高社会服务的功能。江苏省主要依靠轻型制造业的迅速发展，吸引大量农村劳动力和城市劳动力到服务业领域就业，以此推动城市化的发展（陈海燕，2005）。

（二）长三角地区商贸流通业发展情况

长三角是我国经济发展水平最高的区域，既是改革开放的前沿，也是我国经济创新的“主战场”。在三大产业中，以商贸流通业作为重要组成部分的第三产业对长三角的经济社会发展起到了重要的影响作用。改革开放以来，长三角经济迅速发展。上海作为我国经济的龙头，在全国都发挥着示范和带头作用，上海的经济实力、政策环境以及地理优势都存在着较大的比较优势。2001年，上海市对长江三角洲商贸流通业的贡献率就已经达到39.7%，随后由于江苏、浙江的迅速崛起，上海的商贸贡献率有所下降。原因是上海市的产业发展较为粗放，产业涉及不够精细，因此产业的资源配置效率受到了影响。江苏省一直力推商贸流通体制改革，新型的流通方式不断出现，商贸流通业对江苏省的经济贡献度不断增加。在浙江省，商贸流通业是经济发展的先导产业，商贸流通业扮演着桥梁和纽带的作用，推动了浙江省贸易流通多元化、市场化的进程。

实证研究

（一）面板数据模型介绍

面板数据模型的一般形式为：

其中xit为解释变量，为l×k 向量，βit为k×l向量，k为解释变量的数目，i为横截面个数，t为时期（年），un为横截面i在时间t 时的随机扰动项。从式（1）可以看出，模型设定的形式决定了参数估计的有效性，建立正确模型的前提是确定一个正确的模型形式。面板数据模型一般主要有以下三种模型：

变系数模型。变系数模型中的参数不随时间的变化而变化，即表示不存在横截面的结构变化。变系数模型的形式为：

其中δ和β 都是个体时期常量，它们的取值不受时间影响，只受横截面单元不同的影响。

变截距模型。变截距模型是指截距δ在不同横截面上不同，它无法反映观察到的横截面个体上的差异，但这种差异不随个体的变化而变化，是固定的。即个体间的差异只反映在截距项上，其形式为：

混合回归模型。混合回归模型是指δt为常量，表示不存在横截面的个体影响和结构变化，即变截距模型的截距和斜率都为常数，其模型形式为：

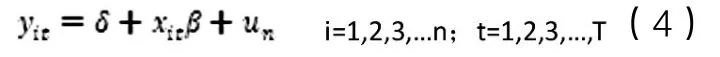
（二）模型建立与数据说明

1.模型形式的确定。本文建立下面两类模型：

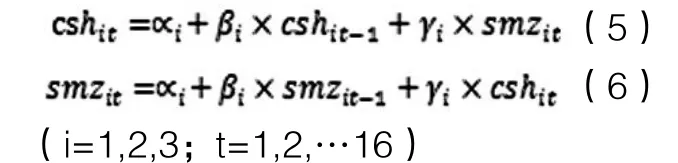
其中1代表的城市上海，2代表的城市是江苏，3代表的城市是浙江，smz代表的是流通产业增加值，csh 代表的是城市化率。t-1表示该指标上一年的值，本文之所以设立一个滞后一期的变量，是考虑到指标不仅受外部因素的影响，同时也受自身发展的影响。

2.数据说明。本文选取的流通产业增加值只包括住宿业、餐饮业和批发零售业的增加值。流通产业的增加值来自江浙沪16个城市的商贸流通业的加总，数据来源于国家统计局网站。本文用城市人口比重法来代表城市化率，其中城市人口和总人口数都来自于各地各年的统计年鉴。同时为了避免数据波动对实证产生影响，笔者将流通产业增加值进行对数化处理（马龙龙，2005）。

（三）实证分析

1.确定固定效应模型。本文通过Stata软件对数据进行hausman检验，输出结果如表1所示。表中检验结果表明，在显著性水平为5%时，拒绝了原假设，所以本文的面板数据模型采用固定效应模型。

2.确定变系数模型。通过F检验确定本文实证模型为变系数模型、变截距模型还是混合模型。通过F检验得：n=3，T=16，K=2。计算可以得到：F1=383.6597，F2=54.0593 。其对应显著性水平为5%的相应临界值是：F0.95（4,39）=3.13，F0.95（6,39）=2.75 。由于F1=383.6597 ＞F0.95（4,39）=3.13，所以拒绝模型为混合模型的假设。由于F2=54.0593 ＞F0.95（6,39）=2.75，所以拒绝模型为变截距模型的假设。因此本文采用的模型应该为固定效应变系数模型。

3.模型参数的估计。由于横截面会经常遇到异方差和时间序列自相关问题。笔者采用似然不相关回归方法对模型进行参数的估计。统计输出结果如下：

第一组：

表1 Hausman 检验结果

表2 面板模型检验结果

表3 原数据的单位根检验

表4 二阶差分的单位根检验

表5 Pedroni 面板协整检验

第二组：

面板模型检验结果如表2所示。

4.模型参数结果分析。第一组的检验结果方程可以得出：一座城市的城市化水平不仅与商贸流通产业具有高度的相关关系，同时也与上一年度的城市化水平高度相关。具体来看：江苏省的流通产业增加值每增加1亿元，其城市化率下降12.46%，上海市流通产业增加值每增加1亿元，其城市化率下降8.03%。笔者分析这种状况出现的原因是：我国实行的“户籍制度”一定程度上影响了城市人口的迁移，造成城市人口统计存在失真现象，影响了城市化率；另外流通产业的迅速发展依赖于科学技术的广泛应用，减少对工人数量的需求，也在一定程度上制约了城市化的进程。而浙江省的实证结果则表明浙江省流通产业发展对城市化率具有正向的影响，即流通产业增加值每增加1亿元，城市化率提高0.04%。笔者认为浙江省主要依靠私营经济，通过市场引导企业，吸引了大量劳动人口从事民营经济，促进了浙江省城市化率的提高。

第二组的检验结果方程表明各省市的城市化率均无形中促进了各地商贸流通产业的发展。具体来看：江苏省的城市化率每提高1%，其流通产业增加值增加0.002亿元；上海市的城市化率每提高1%，其流通产业增加值增加0.25 亿元；浙江省的城市化率每增加1%，流通产业增加值增加0.3031亿元。

5.面板协整检验。首先进行面板单位根检验。通过eviews6.0软件实现原数据的单位根检验，检验结果如表3所示。从表3中可以看出，在5%的显著性水平下，原数据通过LLC检验和IPS检验，即接受存在单位根的假设；在5%的显著性水平下，无法通过Hadri检验，即拒绝不存在单位根的原假设。所以，在5%的显著性水平下，上述两个序列都是非平稳序列。从表4 二阶差分的结果来看，LLC检验和IPS检验结果都表明原数据的二阶差分序列是平稳的。所以，可以确定在5%的显著性水平下，原序列二阶单整。

其次进行面板协整检验。本文采用Pedroni协整检验方法对两个变量进行协整检验，检验结果如表5所示，从Pedroni面板协整检验可以看出，panel-v-statistic，panel-ADF-statistic，group-p-statistic，group-ADF-statistic四个统计量是显著的。所以，在显著性水平为10%时，统计变量拒绝变量之间不存在协整关系的原假设，即城市化与商贸流通产业存在着长期的协整关系（陈继松，2014）。

结论

通过面板数据分析结果来看，虽然长三角地区城市化率与商贸流通产业增加值各自指标值的增长是非平稳的，但长期内两者之间存在着比较稳定的协整关系。流通产业的发展为城市化进程创造力良好的条件，促进城市化的发展。同时城市化的发展也会对商贸流通产业的发展起到促进作用，两者是相互作用的关系。

本文的实证结果表明，可以通过加快商贸流通产业的发展促进城市化的发展。因此我国中西部地区要想加快城市化的进程，必须合理发展商贸流通产业。因为从长三角地区的经验来看，商贸流通产业发展制约劳动力进入城市，阻碍了劳动力的转移，从而影响城市化的进程。同时城市化的推进也要在商贸流通业适度发展的前提下进行，否则容易造成城市居民缺少就业，制约城市化的进程。

在大力发展流通产业的前提下，应结合城市化进程的规划，对流通产业的布局进行合理的安排。特别是在进行新城区规划时，应充分考虑该地区商贸流通产业发展的潜力，切勿盲目进行新城区的规划。另外在城市周围可以积极布局卫星镇，作为城市化功能的补充，进而完善商贸流通网络。

1.陈海燕.我国经济增长与居民消费的面板协整检验[J].统计与决策，2013（9）

2.陈继松.浙江城市化道路的实践与对策[J].城市发展研究，2014（2）

3.马龙龙.流通产业政策[M].清华大学出版社，2005