基于GPU并行粒子群优化的超声弹性实时成像算法

杨先凤，李映洁，赖俊良，彭 博

（西南石油大学计算机科学学院，成都610500）

1 概述

超声弹性成像是一种基于传统超声成像系统的非侵害性影像技术，它能够将局部组织应变映射成彩色编码的图像信息，进而帮助临床医生确定组织硬度及相应的病理情况［1］。但是弹性成像系统在处理时涉及大量复杂运算，使其难以在临床实时系统中得到广泛应用［2］。

为了提高超声弹性成像的质量，同时实现实时成像，本文提出一种基于GPU并行粒子群优化的超声弹性实时成像算法，并通过实验分析该算法。

2 背景介绍

近年来，具有实时弹性成像能力的算法与方法得到了超声工业界更多的关注与应用，如相位零估计（Phase Zero Estimation，PZE）［3］、联合自相关［4］、联合块匹配与光流方法［5］、动态规划［6］和基于先验估计的互相关［7］等方法都已经部署在了商业化的超声成像系统上。这些方法虽然得到了实时帧率，但是它们在提高计算速度的同时又导致了弹性图质量降低等副作用。在较理想条件下，归一化互相关（Normalized Cross Correlation，NCC）算法通常可以提供高质量弹性图［8］，但是在临床条件下，位移估计点易受噪声干扰，因此这种采用孤立估计点计算位移的方式无法满足更高精度的位移估计和生成高精度弹性图的要求。粒子群优化（Particle Swarm Optimization，PSO）算法是一种基于群智能的演化计算技术［9］，该算法通过个体之间的共享机制，使整个集群在解空间中从无序到有序的运动过程，搜索出复杂空间中的最优解。PSO的优点是流程简单、易于实现，算法参数简单，不需要繁杂的调整，同时PSO算法本身具有并行计算的特点。由于大量实验已经证实，对求解最优化问题，粒子群优化算法具有收敛效率高、计算速度快的特点［10－11］。因此，近年来PSO算法被广泛地应用于科学计算、工程应用和社会经济等领域。对于超声弹性的运动追踪和位移估计过程而言，也可看作是一个最优化问题。其目的是寻找能够对压缩前后的RF信号的运动情况进行准确描述的位移场。文献［12］提出一个基于动态规划算法的超声弹性成像方法，该方法设计了一个结合回波幅度相似性与位移连续性的代价函数，并通过动态规划算法优化得到位移场。然而这个方法得到最终的位移场需要多层动态规划方法或解析最小化方法［6］才能获得。本文提出一个基于粒子群优化的超声弹性成像方法，与动态规划多层优化不同，基于粒子群优化算法可以直接得到精确的位移。

随着图形处理器（Graphics Processing Unit，GPU）技术的快速发展，当前GPU已经具有很强的并行计算能力，浮点计算能力可以达到同代CPU的10倍以上［10］。GPU中大部分资源都被设计用来进行数据处理，只有极少数用于数据缓存和指令流的控制［13］。所以在信号和图像处理方面，相对于多核CPU，带有多处理器的GPU具有更为明显的优势［14］。统一计算设备架构（Compute Unified Device Architecture，CUDA）［15］是由 NVIDIA 公司提出的一种基于GPU的并行计算架构，它的推出可以更加方便地在GPU上实现各种领域的科学计算。在CUDA平台下对本文方法进行GPU并行框架设计，使其最终能达到实时的超声弹性成像效果。

3 基于粒子群优化算法的超声弹性成像

3．1 粒子群优化算法

粒子群优化算法利用搜索空间的位置代表候选解，将搜索和优化过程模拟成粒子的位置移动更新过程，每个粒子在搜索时都具有初始速度和位置。在搜索过程中，不仅要考虑自己搜索的历史最佳位置，又要关注领域内其他粒子的历史最佳位置，在此基础上进行位置的变化［16］。将该求解问题的目标函数适应度值用来确定当前粒子的位置好坏，将个体的适者生存过程类比为搜索和优化过程中用较好的可行解来取代较差的可行解的迭代过程。

假设在一个D维空间中，有N个粒子，记粒子i的位置为xi＝（xi1，xi2，…，xiD），其中，xid∈［l，u］，d∈［1，D］，l和u分别为D维空间的下界与上界。将xi代入适应度函数f（xi）求出适应度值；记粒子i的速度为vi＝（vi1，vi2，…，viD），用户指定的Vmax限制粒子速度在一定范围内。记粒子i个体经历过的最好位置为pi＝（pi1，pi2，…，piD）。标准的粒子群算法采用如下公式对粒子速度和位置进行更新［17］：

其中，学习因子c1和c2是非负常数，使粒子具备自我归纳和向群体中良好个体学习的能力，从而向自己的历史最优点和群体内或领域内的历史最优点接近，一般取c1＝c2＝2；r1和r2是随机数，服从［0，1］上的均匀分布；pgbest是粒子群所有粒子中的最好位置；t为迭代次数，一般将最大迭代次数或粒子群迄今为止搜索到的最优满足预先设定的最小阈值作为迭代中止条件。

3．2 超声弹性成像运动追踪与位移估计

假定从压缩组织变形前后得到的RF信号为RF1和RF2。RF1和RF2的尺寸为m×n（m表示一条回波线上采样点的数量，n表示回波线的数量）。这里，适应度函数由标准的回波幅度相似度计算方法构成：

当ER越小，说明2条回波线越相似。在实际的计算过程中，通常可采用一种类似于相关性计算的比较窗口来计算它们的相似性，并且为了避免搜索过程中陷入局部最优，本文采用一种类似于金字塔模式的多层次窗口模式计算对应估计位置的相关性。通常，过高的窗口重叠率会产生蠕虫噪声［18］，采用一定的间隔来计算对应采样点的位移可以满足应用需求，同时也避免了过于密集的计算。因此，对于采样点i对应的总代价函数如下式：

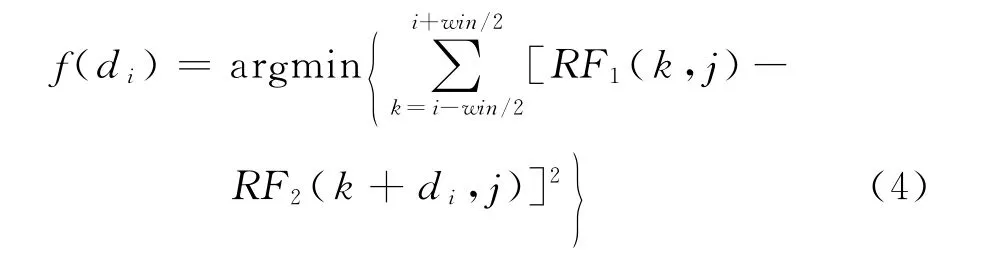
在基于粒子群优化算法中，di是所求的待估计点（待估计窗口）位移，最优di值是通过粒子群优化获得，因此RF2（k＋di，j）的取值必须通过插值方式取得。本文采用线性插值方法。整个总代价函数作为粒子群优化算法中的适应度函数。

本文提出的基于粒子群优化算法的超声弹性成像位移估计的具体实现步骤如下：

步骤1将压缩前后的2个超声回波RF信号文件读入到内存中。

步骤2每一条回波线上的采样点个数为ROW，共有COL条扫描线，设定每一条回波线上的窗口大小为win个采样点，窗口间隔为k，则可以得到待估计点的数量M。用粒子群优化计算每一个待估计窗口的位移delaym，其中，m＝1，2，…，M。

步骤3利用传统的互相关算法求得位于中心位置回波线的位移作为下一步粒子群优化估计的引导位移，这可以减少粒子群优化算法的搜索范围。

步骤4随机初始化每一个粒子的位置Xi和速度Vi。

步骤5从t＝1到最大迭代次数，执行下面的循环：

（1）由式（3）计算出粒子的适应度值fi；

（2）计算粒子的个体最优与群体最优；

（3）通过粒子群优化算法的速度Vi和位置Xi更新式（1）和式（2）对粒子状态进行更新。

步骤6迭代结束以后，得到的群体最优位置和引导位移的和即为待估计点的位移，回步骤4继续下一个待估计点的位移估计。

3．3 并行超声弹性成像框架

从粒子群优化的适应度函数式（3）计算知道，对于每一条信号上每一个窗口的计算都是数据独立的。因此，基于粒子群优化算法的超声弹性成像的并行性主要体现在以下2个方面：

（1）一条扫描线上的每个窗口的位移是可以并行计算的；

（2）每一条扫描线是相互独立的，也是可以并行计算的。

因此，从并行算法的角度，每个待估计点的所在窗口都可以同时进行位移估计，也就是让每一个GPU线程处理一个待估计点所在窗口的所有采样点。进一步需要考虑时如何采用有效的线程结构和优化的存储器以提高带宽的使用率。

在CUDA平台上，warp是调度和执行的基本单位，一个warp包含32个线程。为了防止过小的warp浪费计算资源，每个线程块中线程的数量应该设置为warp尺寸的整数倍，即线程数量的设置至少需要满足的条件是一个线程块内的线程数是32的倍数，并且最好不低于64个。使用纹理存储器是得到高带宽利用率的手段之一，压缩前后的2个I／Q数据帧存放在纹理存储器中。纹理存储器提供的缓存机制使对纹理缓存的拾取只需要一个存储器时钟，这样可以达到较高的读取数据。基于粒子群优化算法的超声弹性成像并行实现的具体实施思路：在GPU中建立所需且有效的线程结构，并为每个待估计点开辟独立的计算空间，同时保证合理的寄存器使用数量，每个线程运行中均会执行PSO算法以针对特定待估计点进行位移寻优。GPU的多核并行特性使多个窗口待估计点位移计算的时间缩短成与一个窗口计算的时间相似，从而提高运算效率。本文方法的GPU并行实现框架如图1所示。

图1 GPU并行框架

由于在仿真实验中验证了较小的种群规模与迭代次数能够实现准确的超声弹性成像的位移追踪。因此，与传统粒子群算法本身的并行不同［19－20］，本文将粒子群优化算法实现为device函数，通过一个并行计算所有估计点的kernel调用即可满足实时计算需求。基于CUDA的并行执行kernel函数如图2所示。

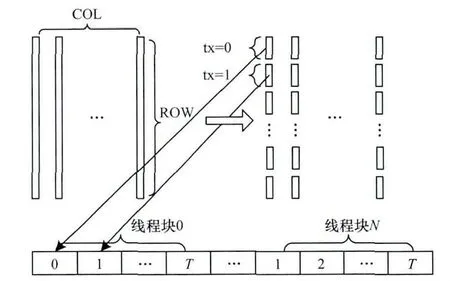
图2 基于CUDA的kernel函数

其算法描述为：

其中，tx代表每一个线程，在＿＿global＿＿函数里面调用粒子群优化算法函数计算每一个窗口的位移，由于使用＿＿global＿＿的函数，只可以在设备上执行，因此要调用粒子群优化函数PSO（），只能将PSO（）作为＿＿device＿＿函数才以在设备上调用，且只可以在设备上调用。PS0（）函数的具体步骤与上一节所述一样。

4 实验与结果分析

4．1 仿真实验

仿真使用文献［19］提出的模拟压缩前后的生物组织变化数学模型。在本文中，仿真的散射子模型内部包含一个硬球，模型的宽度为3cm，深度为3cm，硬球的半径为0．5cm，位于模型内部中间位置。这个模型由200 000个散射子构成，散射子的强度符合高斯分布。

该模型分别考虑到散射的横向和纵向移动，模型中散射子的横向和纵向移动位移定义如下：

其中，R是硬球的半径；r是散射子到坐标中心的距离，并且r2＝x2＋z2；K是硬球的杨氏模量与背景的杨氏模量之比；P是外力应变值，接近等于背景的轴向应变；v（x，z）和u（x，z）分别是散射子的轴向位移和横向位移，本文仅需要轴向位移信息，设定u（x，z）＝0即可。

4．1．1 种群规模与迭代次数对算法性能的影响

种群规模与迭代次数是影响粒子群优化算法的优化精度和收敛速度的2个重要参数，为了解决本文所提出的位移追踪的优化问题，在保证位移追踪精度的同时，选择适合的种群规模与迭代次数对提高算法的计算效率具有重要影响。

通过改变种群规模与迭代次数，评估粒子群优化在寻找最佳适应度值（即最优解）的性能优劣，以及确定算法中所需要的迭代次数。

从图3的实验结果可以看出，在针对位移追踪的优化问题上，粒子群优化算法表现出的特性为：随着种群规模的增大，迭代次数变小，且算法优化精度基本接近。所以PSO算法只需要较少的迭代次数就能获得足够的位移追踪精度。

图3 种群规模与迭代次数对算法性能的影响

4．1．2 位移估计准确性

为了评估粒子群优化算法与传统的互相关算法在位移估计上的偏差，本文分别采用互相关算法和粒子群算法计算位于中心位置的回波线的位移，通过均方根误差方法对得到的位移与理想情况下的位移进行对比分析。

图4显示了基于粒子群优化的运动追踪和位移估计算法与传统的互相关方法（抛物线插值）的位移估计精度。图4（a）为整条回波线的位移比较，从中很难区分2种方法的优劣，它们得到的位移估计值与真实位移值几乎完全吻合。图4（b）为对图4（a）前100多个位移估计点放大图，从图中可以看出，粒子群优化方法得到的位移与真实位移更为接近。显示了粒子群优化方法能获得更好的位移估计精度。而互相关方法与粒子群算法所得到的整条线位移的均方根误差分别为0．007 3和0．006 3。

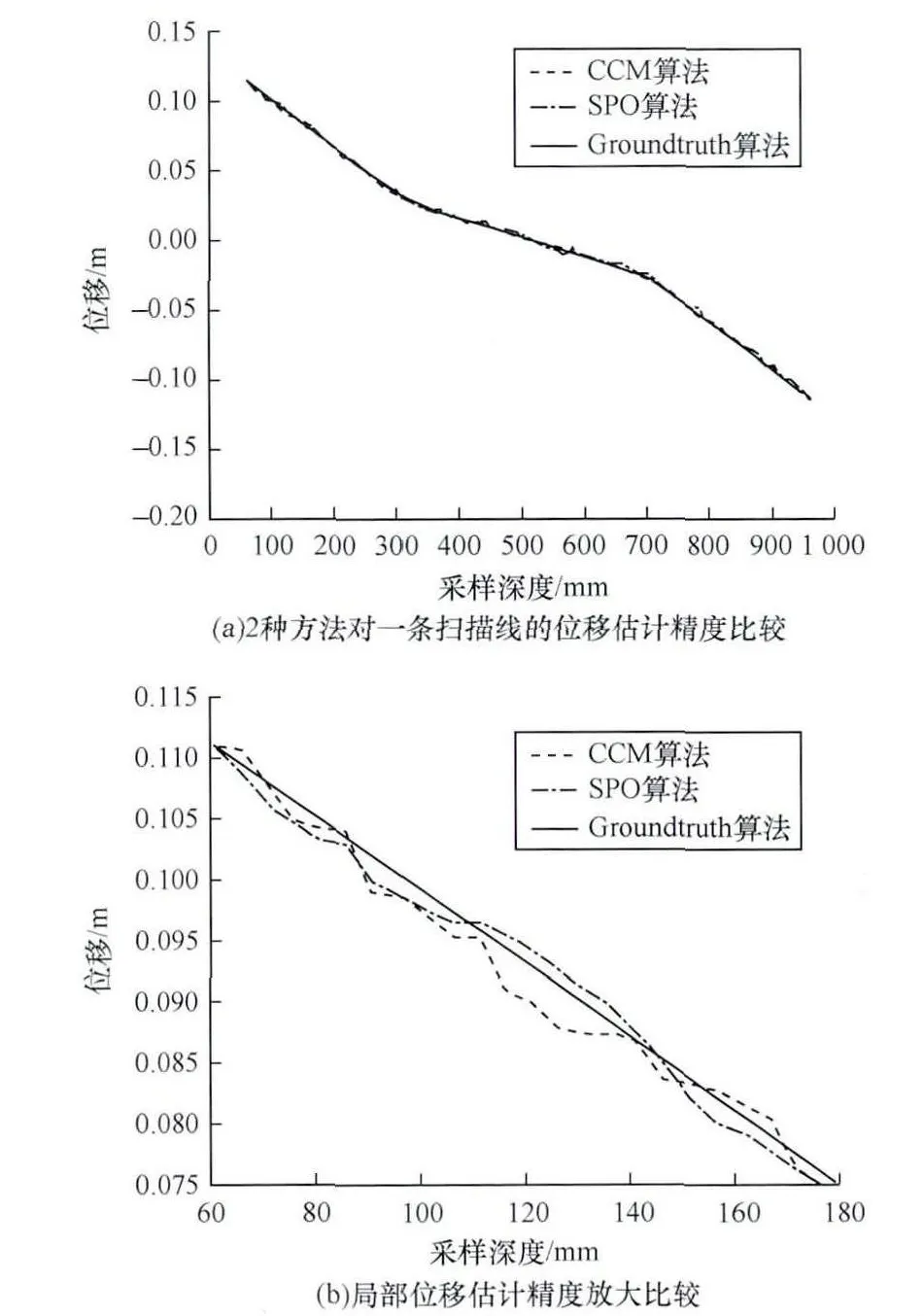
图4 算法真实位移的比较

4．1．3 计算速度

本文中CPU串行计算采用Intel Xeon E3－1220 CPU，GPU并行计算采用NVIDIA Tesla K10GPU卡实现，K10共有3 072个流处理器核和8GBDDR5内存。CUDA驱动版本为5．0，使用VS 2008作为编程工具。

表1为粒子群优化算法的CPU串行实现与粒子群优化算法的GPU并行实现的运行时间对比结果。为了公平起见，CPU和GPU实现都采用相同的参数设置，计算时窗口大小设置为20个采样点，相邻窗口的重叠部分为75%，种群数量为20，迭代次数为15次。表中加速比为本文所提方法的CPU串行实现与GPU并行实现的比较结果。表1中前3行的计算结果针对原始RF信号行不变，而回波线的数量成倍增加。而后3行的计算结果针对原始RF信号保持列不变，采样点数量逐步成倍增加。从表1中可以得出，不管数据大小为多少，与本文方法的CPU实现相比，该GPU并行实现方法获得了较好的加速比。针对行保持不变的数据，加速比有小幅度的变化；而针对列保持不变的数据，采样点的数量对加速比却有较大的影响。表1中基于GPU并行实现的计算时间和加速比验证了本文方法的并行计算框架能够通过GPU实现超声弹性成像位移估计算法，在处理512×128的数据规模时其GPU实现处理时间仅为12 ms，可以满足一般标准输出条件下的实时超声弹性成像的需要。

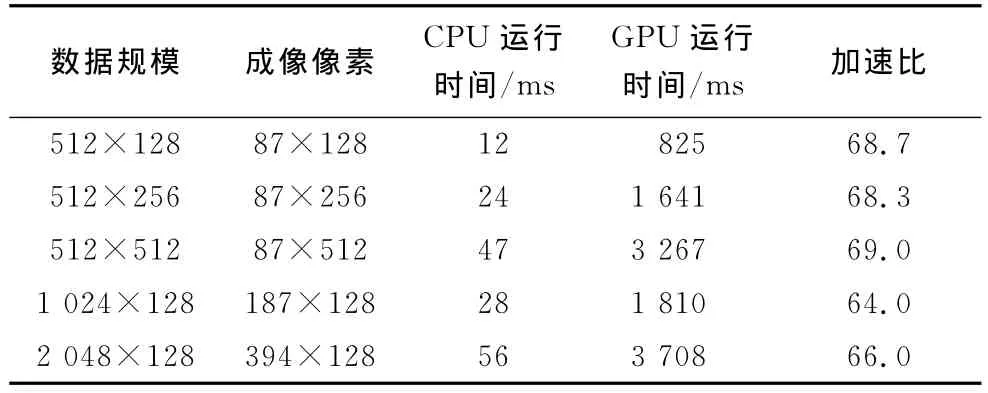
表1 CPU串行与GPU并行时间对比

4．1．4 仿真成像结果

图5显示了基于粒子群优化的运动追踪和位移估计算法与传统的互相关方法（抛物线插值）在仿真数据情况下产生的应变图。在图5（a）中，得到的应变图有几处明显的白色跳变区域。这说明互相关方法在计算位移时容易受到噪声数据的干扰，这种干扰造成位移的错误计算，以至于应变估计放大了这种位移错误。图5（b）显示了粒子群优化得到的应变图，图中无明显跳变错误，这说明粒子群优化具有较好的抗噪能力。

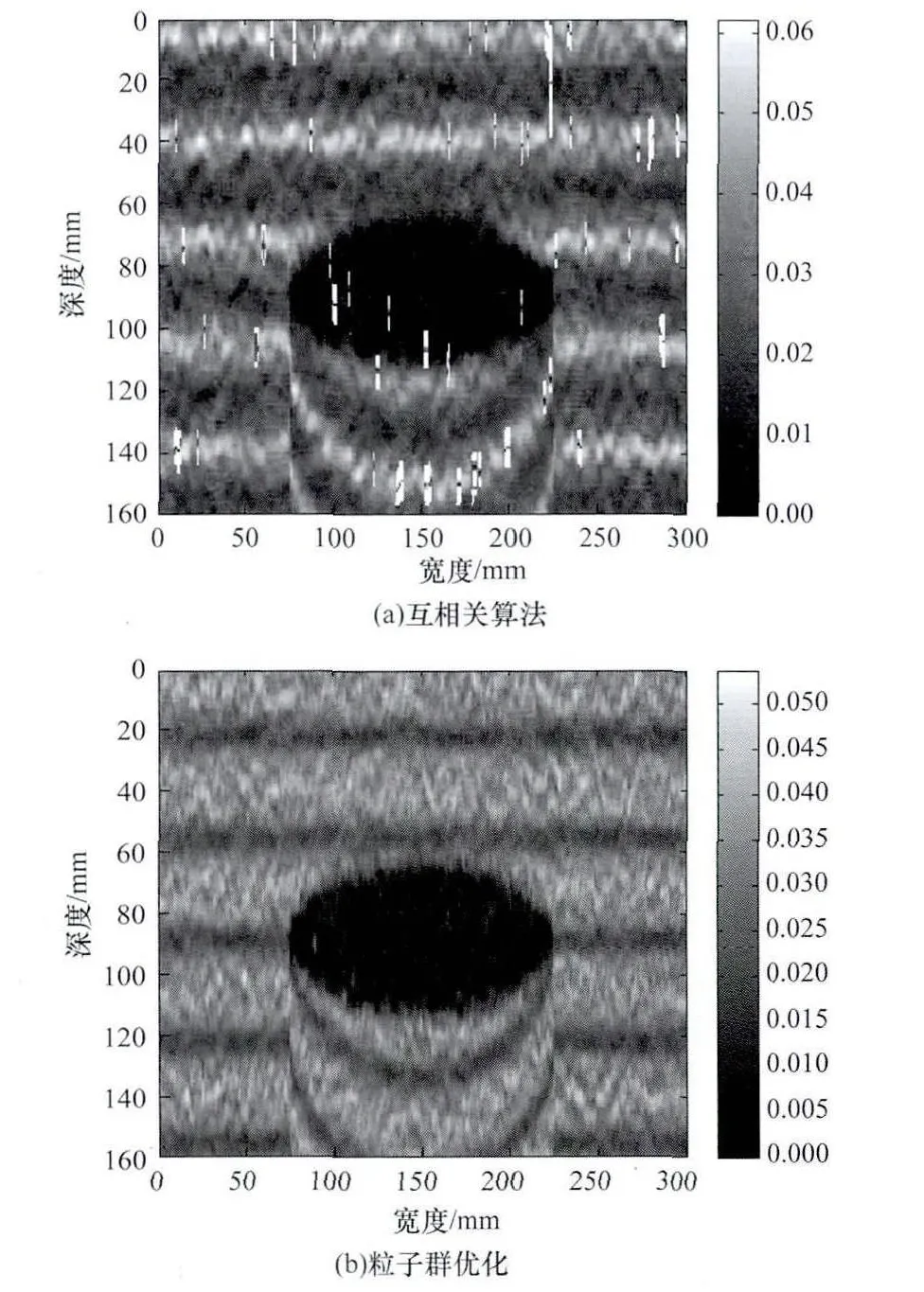
图5 2种算法生成的应变图

4．2 体模实验

体模实验采用专用于弹性成像研究的Model 049弹性体模出来的实时扫描射频回波信号进行体模实验。本实验选择的成像物体直径为10mm、弹性模量为63kPa的硬包容物（Type IV）。实验用探头型号为SA5L38B的128阵元的线阵探头，中心频率为5MHz，75%的分数阶带宽。实验使用的超声系统是iMago C21超声机，系统RF信号采样频率设为40 MHz。在数据采集过程中，未使用任何额外的控制设备情况下保持在一个恒定的速度将探头进行徒手轴向压缩／释放。

图6为对压缩前后的2帧信号，分别采用互相关分析和粒子群优化方法的串行和并行方法计算得到的弹性图，从图中可以得到，在真实体模数据情况下，粒子群优化的2种方法都能获得较好质量的弹性图。

图6 体模数据产生的弹性图

图6（c）所采用的并行粒子群优化算法为了提高计算速度采用的计算精度是单精度，算法实现过程中的一些数学函数也采用的是低精度的版本，但是对于本文中的弹性成像的应用是足够的。从视觉上来看，图6（b）和图6（c）2种方法几乎没有任何差别，这也说明文中所选择的种群数量和迭代次数都是合适的。

5 结束语

本文将群智能算法中的粒子群优化算法应用于超声弹性成像中，通过CUDA平台并利用GPU实现高效并行计算。实验结果表明，本文算法不仅能够获得较好的位移质量，同时GPU并行实现的方法能够保证弹性图的实时处理。本文算法的提出对于拓展群智能算法的应用领域具有积极作用，同时对于超声弹性成像中的最优化问题求解也具有重要的现实意义，下一步将对本文算法继续进行临床数据测试，并优化其GPU的并行实现性能。

［1］彭 博，谌 勇，刘东权．基于GPU的超声弹性成像并行实现研究［J］．光电工程，2013，40（5）：97－105．

［2］张 霞，何兴无．CUDA平台下的超声弹性成像并行处理算法［J］．计算机与数字工程，2012，（9）：113－116．

［3］Lindop J E，Treece G M，Gee A H，et al．3DElastography Using Freehand Ultrasound［J］．Ultrasound in Medicine ＆ Biology，2006，32（4）：529－545．

［4］Shiina T，Nitta N，Sjsum E U，et al．Real Time Tissue Elasticity Imaging Using the Combined Autocorrelation Method ［J］．Journal of Medical Ultrasonics，2002，29（3）：119－128．

［5］Zhou Yongjin，Zheng Yongping．A Motion Estimation Refinement Framework for Real－time Tissue Axial Strain Estimation with Freehand Ultrasound［J］．IEEE Tran－sactions on Ultrasonics，Ferroelectrics and Frequency Control，2010，57（9）：1943－1951．

［6］Rivaz H，Boctor E，Foroughi P，et al．Ultrasound Elastography：A Dynamic Programming Approach［J］．IEEE Transactionson Medical Imaging，2008，27（10）：1373－1377．

［7］Zahiri A R，Salcudean S E．Motion Estimation in Ultra－sound Images Using Time Domain Cross Correlation with Prior Estimates ［J］．IEEE Transactions on Bio－medical Engineering，2006，53（10）：1990－2000．

［8］Hoyt K，Forsberg F，Ophir J．Comparison of Shift Estimation Strategies in Spectral Elastography［J］．Ultra－sonics，2006，44（1）：99－108．

［9］Kennedy J，Kennedy J F，Eberhart R C．Swarm Intelligence［M］．［S．l．］：Morgan Kaufmann，2001．

［10］左颢睿，张启衡，徐 勇，等．基于GPU的并行优化技术［J］．计算机应用研究，2009，26（11）：4115－4118．

［11］王燕燕，葛洪伟，王娟娟，等．一种动态分组的粒子群优化算法［J］．计算机工程，2015，41（1）：180－185．

［12］Rivaz H，Boctor E M，Choti M A，et al．Real－time Regularized Ultrasound Elastography［J］．IEEE Transactions on Medical Imaging，2011，30（4）：928－945．

［13］刘 丹，赵广辉，夏红霞，等．GPU加速分子动力学模拟的热力学量提取［J］．计算机应用研究，2010，27（5）：1820－1822．

［14］Zhao Jieyi，Tang Min，Tong Ruofeng．Connectivitybased Segmentation for GPU－accelerated Mesh Decompression［J］．Journal of Computer Science and Technology，2012，27（6）：1110－1118．

［15］都志辉，李三立．高性能计算之并行编程技术——MPI并行程序设计［J］．北京：清华大学出版社，2001．

［16］Spears W M，Green D T，Spears D F．Biases in Particle Swarm Optimization［J］．International Journal of Swarm Intelligence Research，2010，2（1）：34－57．

［17］张维存．蚁群粒子群混合优化算法及应用［D］．天津：天津大学，2007．

［18］崔少国，刘东权．使用二维小波收缩法去除弹性成像蠕虫噪声［J］．生物医学工程学，2011，8（3）：460－464．

［19］陈 风，田雨波，杨 敏．基于CUDA的并行粒子群优化算法研究及实现［J］．计算机科学，2014，（9）：263－268．

［20］蔡 勇，李光耀，王 琥．基于CUDA的并行粒子群优化算法的设计与实现［J］．计算机应用研究，2013，29（8）：2415－2418．