递归流分类算法研究与改进

余 虎，黄 宇

（合肥工业大学计算机与信息学院，合肥230009）

1 概述

流分类技术［1］根据事先设定好的一组策略和规则，将数据包区分为特定种类的数据流，事先设定的策略和规则集合组成规则表。随着网络流量迅速增长，流分类技术成为路由器、防火墙等网络设备的关键技术之一。还应用于IP网络QoS模型［2］中，对不同等级的业务流进行分类和调度，以提供不同级别的服务质量［3］。

递归流分类（Recursive Flow Classification，RFC）算法［4］是一种多维流分类算法，具有分类速度快、支持前缀匹配等优点。然而，随着规则表规模的增加，对内存空间的需求也迅速增加［5］。针对这一缺点，许多学者提出了不同的改进算法，文献［3］提出利用比特位图（BitMap）位来表示独立元素分布的改进算法，改善空间使用效率，但并没有解决独立元素的重复存储问题；文献［6］提出改变缩减树的存储结构的改进算法，消除交叉乘积表中重复存储元素，一定程度压缩内存空间，但存在算法设计复杂、预处理时间过长等问题；文献［7］提出利用或运算压缩块比特位图（Chunk BitMap）向量表的Merge＿RFC算法，进一步避免了交叉乘积表中由于规则分布稀疏所造成的空间浪费问题。

本文对RFC算法进行改进，通过异或运算压缩规则表中块存储位数，降低等价类表和交叉乘积表的内存消耗。

2 RFC算法

RFC算法包含预处理阶段和查找阶段。预处理阶段由一系列递归归并组成，查找阶段是对到达的数据包进行提取关键字和查找索引表操作。

2．1 预处理阶段

预处理阶段主要分为以下4个部分：

（1）将规则表划分成7个块 （Chunk0－Chunk6），其中IP地址域划分成高16位和低16位。Src Addr表示源IP地址，Chunk#0表示高16位源IP地址块号，Chunk#1表示低16位源IP地址块号；Dst Addr表示目的IP地址，Chunk#2表示高16位目的IP地址块号，Chunk#3表示低16位目的IP地址块号；Pro表示协议号，块号为Chunk#4；SPort表示源端口号，块号为Chunk#5，DPort表示目的端口号，块号为Chunk#6。

（2）根据规则表分别生成7个块对应的等价类表，等价类表以块比特位图（CBM）值为内容，等价类标识eqID（Equivlance Class ID）值为索引。再计算每个块在不同情况下对应的eqID值，建立以eqID值为内容的预处理表。

（3）根据第（2）步中的等价类表，对表项按位交叉相与，计算该步的等价类表；再根据等价类表得到交叉乘积表。交叉乘积表的内容是等价类表中eqID值。

（4）采用类似第（3）步的操作，得到交叉乘积表和等价类表，预处理完成。

2．2 查找阶段

对到达的数据包，提取关键字段值并根据预处理阶段分块格式进行分块；再对每块在相应的向量表中找对应索引值（Index），按照预处理阶段的归并路径，查找索引表，直到找到数据包的最佳匹配规则，获得分类标识（ClassID），完成查找过程。

3 Optimize＿RFC算法

3．1 Optimize＿RFC算法的提出

RFC算法预处理时，等价类表和交叉成绩表占用大量的内存空间，等价类表的长度由规则数目所决定［8］。当规则表过大时，会导致等价类表长度急剧增加。此外，等价类表交叉相与生成交叉乘积表，因此，当等价类表长度增加时又会造成交叉乘积表聚合增大。

文献［9］对RFC算法的IP地址域进行4位异或操作，先将源IP地址和目的IP地址分割为高低16位，再分别将分割后高低16位压缩到4位，在一定程度上减少了预处理阶段的内存消耗；但文献［9］对IP地址域进行分割操作后，又对块的位长进行压缩，造成块冗余。

本文基于RFC算法提出改进算法Optimize＿RFC，利用异或运算对块的位数进行压缩，且不对IP地址域划分高低16位。将源／目的IP地址分别由32位压缩到8位，端口号由16位压缩到8位，协议字段不进行压缩操作，生成5个块，相对于RFC算法，减少了2个块，并且压缩了等价类表，从而降低预处理阶段的内存消耗。

3．2 Optimize＿RFC算法描述

分类规则表如表1所示。规则分5个域，分别是源IP地址 （Op＿SIP）、目的IP地址 （Op＿DIP）、协议号 （Op＿Pro）和源端口号 （Op＿SPort），目的端口号（Op＿DPort），ClassID表示规则号，Opt表示操作。

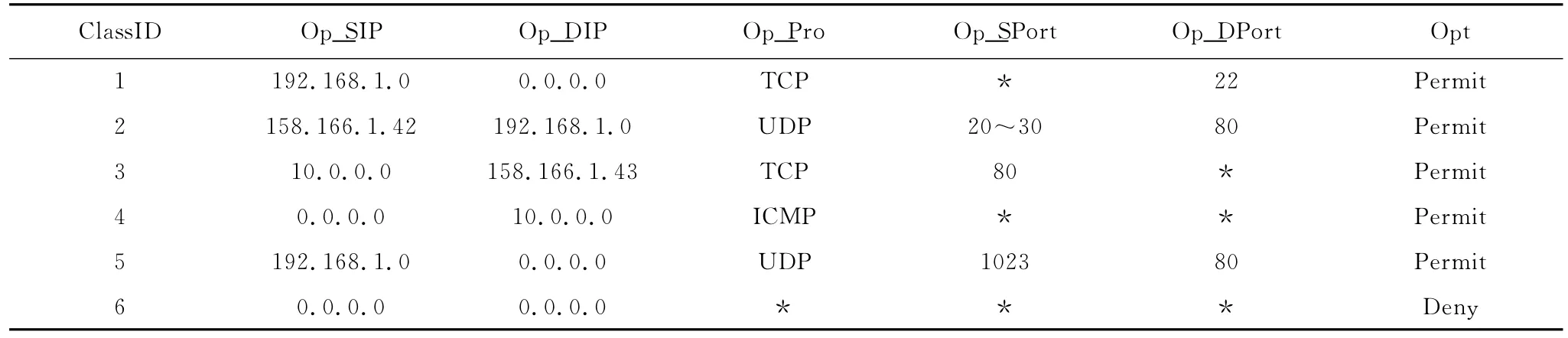
表1 分类规则

Optimize＿RFC算法分为预处理阶段和查找阶段。

3．2．1 预处理阶段

预处理阶段主要分为以下2个部分：

（1）规则表压缩。

对表1中32位源／目的IP地址字段分别按4位进行异或，压缩成2个8位的块（chunk#00，chunk#01）；对16位源／目的端口号字段分别按2位进行异或操作，压缩成2个8位的（chunk#03，chunk#04）；协议字段单独构成一个块chunk#02。

IP地址字段异或压缩过程如图1所示。

图1 IP地址字段异或压缩过程

（2）生成预处理表、等价类表和交叉乘积表。

针对查找阶段的4步：phase0～phase3，为查找阶段提供预处理表，等价类表以及交叉乘积表。

1）根据表1压缩后的5个块分别生成对应等价类表，在 phase0中用 Op＿eqID00－Op＿eqID04表示，Op＿eqID表描述每个eqID对应CBM位串。等价类表以CBM值为内容，eqID为索引；再根据等价类表生成对应预处理表，以eqID值为内容。Optimize＿RFC算法的eqID和CBM值计算同RFC算法。

2）对phase0生成的等价类表进行逐项相与操作，将 Op＿eqID00和 Op＿eqID02表项内容相与，Op＿eqID01，Op＿eqID03和 Op＿eqID04相与，分别得到phase1的交叉乘积表chunk#10，chunk#11，并计算相应的等价类表。

3）根据phase1的等价类表，利用同样的方法，计算得到phase2的交叉乘积表及对应的等价类表。

3．2．2 查找阶段

查找阶段分为以下2步：

（1）数据包关键字压缩。

当数据包到达时，提取头部关键字段值，并进行压缩，压缩方法同3．2．1中的第（1）步。

儿童贫血是临床常见疾病,据报道中国5岁以下儿童贫血率为12.6%,引起贫血的主要因素是:膳食结构、生活习惯、遗传因素,主要类型为:地中海贫血与缺铁性贫血。临床症状主要为食欲不振、肝脾肿大、皮肤黏膜苍白等。[1]并且贫血可影响到患儿的生长发育、免疫发育、智力与心理的发展。文山地区属于地中海高发地区,但是地中海贫血与缺铁性贫血的治疗方法也不尽相同,两者常规检查结果相似性较高,诊断鉴别具有一定难度,在实际过程中,目前以血液检验为主要手段。因此,本文旨在探讨血液检验应用于小儿贫血中的鉴别意义。

（2）查找阶段共分为4步，如图2所示。

假设到达数据包关键字值是158．166．1．42（Op＿SIP），192．168．1．0（Op＿DIP），udp（Op＿Pro），23（Op＿SPort），80（Op＿DPort）。

1）通过异或运算分别计算每个块的索引（Index）。得到源IP地址索引值为3，目的IP地址索引值为20，协议号索引值为17，源端口号索引值为23，目的端口号索引值为80。

2）根据phase0的等价类表和Index公式［10］计算phase1的索引 值。Index＝Ci，j＊N＋Ci，j＋1＋…＋C00（Ci，j为chunk#ij的索引值，N为chunk#（i，j＋1）等价类表大小）。通过计算得到chunk#10、chunk#11索引值分别为9和7。

3）再根据phase1的索引值以及Index公式计算得到phase2中交叉乘积表索引值为5。

4）根据phase2的等价类表以及索引值得到最终查找结果，对应CBM值为010001。再对最终查找结果进行顺序查找，获得最终匹配的规则2。

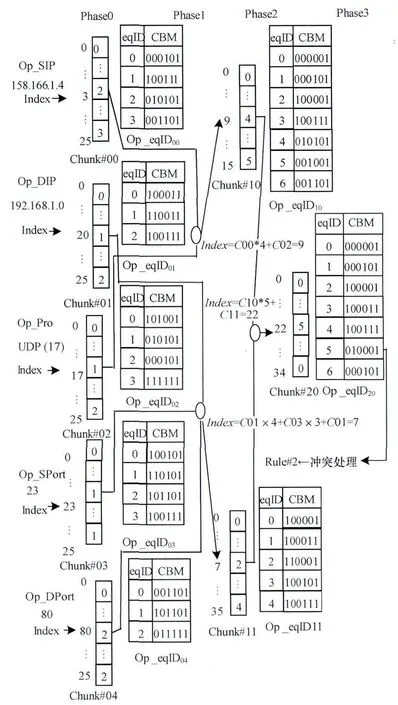
图2 Optimize＿RFC算法查找过程

3．3 算法分析

算法分析过程如下：

（1）空间复杂度。

Optimize＿RFC算法与RFC算法相比，在存储开销上会大大降低。在预处理阶段，RFC算法中每块数据有S位，Optimize＿RFC算法将数据块由S位压缩到8位（2S≥28），N条规则中每块的等价类表也相应的压缩，并且phase0的预处理表和等价类表由原先的7个降低到5个。由于是利用顺序查找的方法解决最后匹配规则可能存在的冲突，因此需要额外的存储空间保存最后阶段的CBM表。

Optimize＿RFC算法与文献［9］算法相比，在预处理阶段预处理表和等价类表个数各减少2个。

（2）时间复杂度。

与RFC算法相比，由于Optimize＿RFC算法在预处理阶段进行大量异或处理操作，因此Optimize＿RFC算法的预处理时长会相对增加。Optimize＿RFC算法在各个阶段的查找速度与RFC算法基本相当，只多出最后阶段的冲突处理时间。冲突处理时间由冲突量决定，冲突量取决于规则表规模，因此查找阶段时间复杂度增加O（N）。

与文献［9］算法相比，Optimize＿RFC算法在预处理阶段与文献［9］执行相同次数的异或操作，查找阶段也有相同的冲突处理，因此，两者时间复杂度相近。

4 实验结果与分析

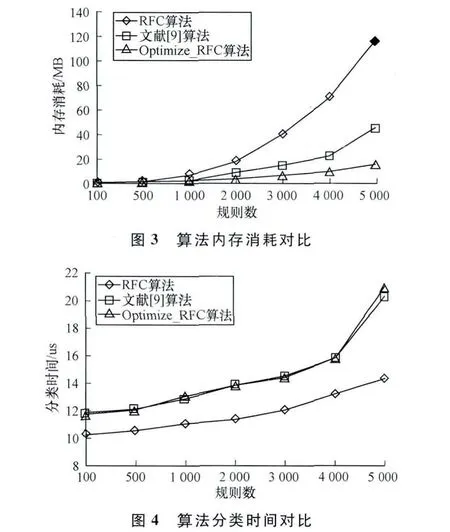
本文对Optimize＿RFC算法以及RFC算法、文献［9］算法进行仿真实验，运行环境为Thinkpad E420（Intel coreI5 2．4GHz CPU，2GB 内 存 ）PC 机、Windows XP3系统。规则表和对应的分类数据包由ClassBench［11］产生，规则表规模为100条～5 000条。统计出各算法的内存消耗和分类速度。

由图3和图4的实验结果表明，RFC算法在预处理阶段需要大量的存储空间，当规则表规模超过一定大小时，RFC算法可能存在内存溢出。Optimize＿RFC算法在分类速度上略慢于RFC算法，但是内存消耗方面，随着规则表规模的增加，Optimize＿RFC算法的空间性能要优于RFC算法。并且相对于文献［9］算法，Optimize＿RFC算法的空间性能也要更好。

5 结束语

针对RFC算法运行时存在存储空间的不足，本文提出一种基于内存优化的改进算法Optimize＿RFC算法，该算法可以有效减少RFC算法的内存开销，同时保持相对较快的流分类速度。实验结果表明，当规则表超过一定规模时，RFC算法的内存消耗会急剧增加，而Optimize＿RFC算法通过对等价类表进行异或处理，可以有效改善因规则表规模过大造成内存消耗过大的问题。Optimize＿RFC算法可以提高递归流分类算法效率，但是并没有解决规则集的动态更新［12］问题，可作为流分类算法的进一步研究方向。

［1］Gupta P，Mckeown N．Packet Classification on Multiple Field［C］／／Proceedings of ACM SIGCOMM’99．New York，USA：ACM Press，1999：147－160．

［2］Babulak E．User’s Perception of Quality of Service Provision［C］／／Proceedings of IEEE International Con－ference on Industrial Technology．Washington D．C．，USA：IEEE Press，2003：1022－1025．

［3］Spitznagel E． Compressed Data Structures for Recursive Flow Classification［C］／／Proceedings ofIEEE WUCSE’03．Washington D．C．，USA：IEEE Press，2003：984－992．

［4］Gupta P， Mckeown N． Algorithms for Packet Classifica－tion［J］．IEEE Network，2001，15（2）：24－32．

［5］Berndt D，Fisher J，Joshson L，et al．Breeding Software Test Cases with Genetic Algorithms［C］／／Proceedings of the 36th Hawaii International Conference on System Sciences．Big Island，USA：［s．n．］，2003：338－349．

［6］刘 铎，华 蓓，唐锡南，等．Compact RFC：一种内存优化的RFC包分类算法［J］．小型微型计算机系统，2007，28（3）：482－487．

［7］曹 婕，陈 兵．一种内存优化的RFC包分类算法Merge＿RFC［J］．小型微型计算机系统，2012，33（4）：865－868．

［8］亓亚烜，李 军．高性能网包分类理论与算法综述［J］．计算机学报，2013，36（2）：378－382．

［9］刘 胤，杨世平．基于RFC算法的快速多维数据包分类算法［J］．计算机工程，2008，34（6）：95－97．

［10］陈 胜，张大方，毕夏安．一种基于流的局部特性和多级查找的高效包分类算法［J］．小型微型计算机系，2013，34（11）：2499－2503．

［11］Taylor D E．Class Bench：A Packet Classification Benchmark［J］．IEEE／ACM Transactions on Networking，2007，15（3）：499－511．

［12］Trivedi U．An Optimized RFC Algorithm with Incremental Update［C］／／Proceedings of International Conference on Advances in Computing Communications and Informatics．Washington D．C．，USA：IEEE Press，2014：120－127．