土地储备项目风险评估的计量分析

许亚东，周一成，马 可，张 俊

（1．安徽财经大学经济学院，安徽 蚌埠233030；2．安徽财经大学国贸学院，安徽 蚌埠233030）

土地储备，是指国土资源管理部门为实现调控土地市场，依法通过收回、收购、征用或其他方式取得土地使用权的土地，并向社会提供各类建设用地的行为。近年来，国内外学者对土地收储风险防控进行了大量研究。如罗玲运用现金流分析法及统计学有关理论对土地储备投资风险进行测度［1］；任奎等通过定量化测度南京市城市土地储备规划风险，得出南京市较大风险级别的面积比例达到了66%以上［2］；陈晓军等利用不可修复可靠性串联模型建立时间序列回归判别模型，提出土地储备项目风险预警控制方法［3］。

这些研究多是针对具体的土地项目财务平衡模型，通过文献资料法等对某一地区进行实证研究。而将模糊数学理论应用于项目评估，并建立普适性的风险评价模型的研究则较少。为此，在新时期完善已有的风险评估方法，且对合理选择开发项目、充分利用土地资源、获取更大效益均具有重要意义。因而本文基于Fuzzy-AHP方法，在运用主成分分析算法提取出土地储备项目风险的评价指标基础上，建立模糊层次评价体系，对土地储备项目的风险评估进行有效评价。最后，本文通过均值聚类迭代计算指标的变化范围，从而构建完整严密的风险控制体系。

一、风险评估与相关评价指标的联系

（一）土地项目的经济风险指标

1、财务净现值 （FNPV）与财物内部收益率（FIRR）

对具有常规现金流量（即在计算期内，开始时有支出而后才有收益，且方案的净现金流量序列的符号只改变一次的现金流量）的投资方案，其财务净现值是折现率i的函数，其表达式如下：

其中FIRR为财务内部收益率；CI为现金流入量；CO为现金流出量；（CI-CO）t为第t年的净现金流量；n为项目计算期。

随着折现率的逐渐增大，财务净现值由大变小，FNPV与i之间的关系一般如图1所示。

图1 常规投资项目的净现值函数曲线

按照财务净现值的评价准则，i可以大到使FNPV（i）＝0，这时FNPV（0）曲线与横轴相交，达到了其临界值i＊，将i＊称为财务内部收益率。其实质就是使投资方案在计算期内各年净现金流量的现值累计等于零时的折现率［1］。

2、全部投资内部收益率与自有资金内部收益率

设项目的全部投资为P，其中自有资金为Pm，银行贷款额为PL，全部投资内部收益率为IRR，自有资金的内部收益率为IRRm，银行贷款利率为IL，根据3者的关系可得：

令k＝Pm／P

其中k为自有资金在全部投资中的比例，通常规定k≥0．25，β为贷款资金在全部投资中的比例。

（二）经济风险指标的主成分分析

1、数据处理

在社会经济、管理、等众多领域的多指标体系中，如节约型社会指标体系等，主成分分析法常被应用于综合评价与监控［4］。因此要构建风险评价模型，需要从众多项目风险的财务指标中进行降维处理，从而为下文层次分析法模型的构建选择合适的指标。本文选择土地项目的收购储备面积，财务净现值FNPV，财物内部收益率FIRR，动态回收周期Pt，项目投资总额估算（万元），自有资金，贷款资金，贷款比例这8个因素进行主成分分析。

2、模型的构建与求解

将其代入MATLAB程序中进行主成分分析［5］的求解，从而求出主成分的个数t＝4，并且4个主成分对应的特征值分别为（3．0495 2．3485 1．0343 0．6885）。

因而可得到4个主成分的表达式如下所示：

3、结果分析

对以上4个主成分的向量权值进行分析，把每一个因素的权值进行加权平均，见表1。

表1 主成分指标因素的向量权值

从表1中可以看出，收购储备面积和贷款比例因素对主成分的影响比较明显，其次是财务净现值，动态回收周期，财物内部收益率，影响比较小的是贷款资金，项目投资总额估算和自有资金。

二、土地储备项目的风险评估方法

（一）Fuzzy AHP方法确定指标权重

1、研究思路

Fuzzy-AHP评价方法是基于模糊数学理论（Fuzzy）与层次分析方法（AHP）相结合，通过层次分析方法确定评价指标权重，再进一步通过模糊综合评判进行准确评价的数学方法［6］。本文应用层次分析法的基本原理构建风险评估指标的层次分析模型，建立相应的稳定性评价指标体系，将指标间相互比较矩阵的特征向量作为指标评价因子的权重，从而为下文模糊综合评价模型提供分析指标。分析土地储备项目的风险，首先要确定相关评价指标的权重。由以上主成分模型可知，收购储备面积、贷款比例、财务净现值、动态回收周期、财务内部收益率对主成分影响明显，可以根据主成分中因子负荷量来构造比较判断矩阵［7］，对因子负荷量较大的指标，赋予较高判别相对数。

2、模型的构建与求解

根据主成分因子负荷量，构建比较判断表，如表2。

表2 评估项目风险的比较判别表

通过一致性检验［8］，认为其比较判断矩阵的不一致程度在容许范围之内，故可用来计算权重。

3、结果分析

通过MATLAB程序计算得出每个因素的权重，如表3。

表3 主成分指标的权重

（二）模糊综合评价确定项目风险评估方法

1、研究思路

模糊综合评判是在模糊数学理论的基础上，对受多种模糊因素影响的事物功能或现象进行总体综合评［6］。本文基于模糊数学理论构建影响因素集的隶属函数，得到土地储备项目的模糊评判矩阵，再进一步计算得到评价结果向量。最后通过模糊综合评判，对主成分影响明显的指标进行综合评价［9］。本文采用相对偏差模糊矩阵进行分析，结合Fuzzy AHP方法所求得的权重，来判断土地储备项目的优劣。

2、模型的构建与求解

（1）设有U ＝ u1，u2，…u ｝｛74为待评价的74个项目集合，V ＝ v1，v2…v ｝｛5是5个评价因素集合，将U中的每个方案用V中的每个因素进行衡量，得到一个观测值矩阵；

（2）由层次分析法所确定的权重，建立综合评价模型：

若Ft＜Fs，则第t个方案优于第s个方案。

3、结果分析

利用EXCEL软件将数据进行处理后，得到了相对偏差模糊矩阵如下所示：

然后通过加权求和，解出Fj，得到74项方案的风险度。如表4。

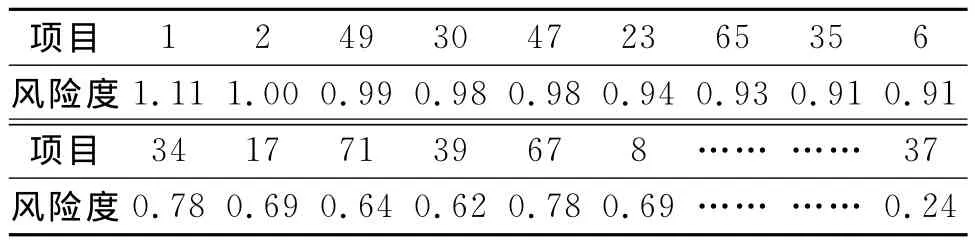
表4 项目风险排序表（按风险度降序排列）

三、风险评估评价指标变化范围

（一）模糊C均值聚类分析

1、研究方法

聚类是一种非监督模式识别问题，它是指按照某种相似性的度量，使相似的样本对象归为相同的类，不相似的样本对象归为不同的类［10］。研究土地储备项目的风险评估方式，就必须要明确该种方式的评估适用范围。为此，本文首先利用模糊C均值聚类模型，得出74个项目聚类中心及隶属度矩阵［11］，在此基础上将74个项目进行分类，进而分析不同类别项目的各项指标值，建立财务内部收益率、融资成功率、动态回收周期以及收益补偿风险值对项目综合评价的线性回归模型。其次针对某类项目一个评级指标，利用控制变量法对其余各项评价指标取平均值固定，推出针对此类项目不同评级指标对应的迭代方程，最后综合考虑各类项目的各指标变化范围，得出各评价指标的允许变化范围。

2、模型的构建与求解

运用模糊C均值聚类［12］进行分类，目标函数相应如下：

3、结果分析

运用MATLAB软件，得出聚类中心及隶属度矩阵，然后在隶属度矩阵的基础上，通过相应程序对各个项目进行分类，检索其类别所属，得到结果如表5。

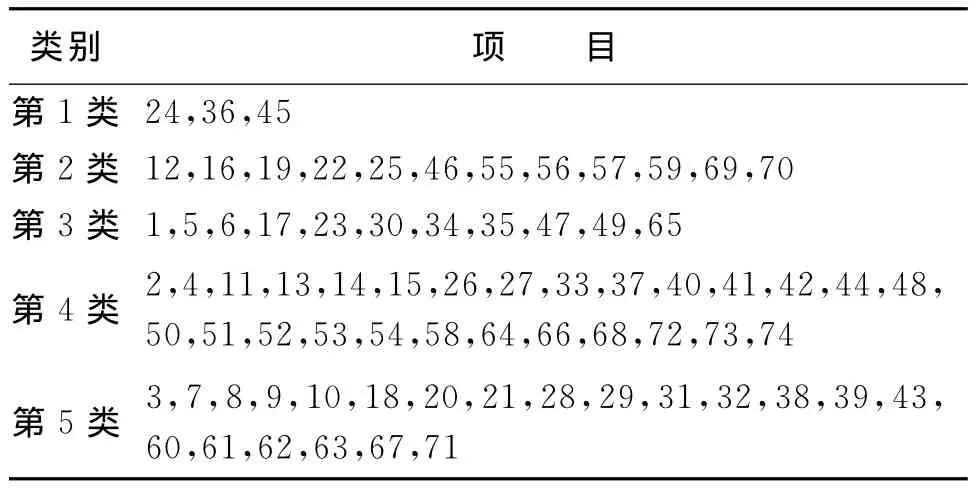
表5 各类别项目表

在此基础上分别分析各类项目的风险度情况，利用EXCEL做出项目风险分布图，如图2。

图2 项目风险度分布图

（二）多元线性回归分析

1、散点图初步判断

通过分析每一类项目，运用MATLAB软件，做出财务内部收益率、财务净现值、动态回收周期以及收购储备面积与项目风险度之间的散点图（见图3），因而可以建立多元线性回归模型。

从图4中可以清晰地看出，项目风险度Fj与各项评价指标数值之间均存在近似的线性关系，可以验证处理后的数据进行多元线性回归是合理可行的，具有很强的说服力和实际应用性。

2、模型的构建与求解

图3 Fj 分别与四项评价指标y1i、y2i、y3i、y4i的散点图

运用MATLAB编程中Regress命令求出总项目风险度Fj与各项评价指标之间的多元线性回归模型，可以得到如下回归方程：

且可决系数R2＝0．9702＞0．8，统计量F＝561．92，故拟合效果较好。

（三）控制变量法分析

1、研究思路

利用多元线性回归模型所求出的回归方程，以及模糊C均值聚类分析所得到的5类项目，对影响项目总评价的各指标列进行分析。首先，利用控制变量法［13］，在考虑财务内部收益率对综合评价影响的同时，对其余的3项指标进行取同一类的均值进行固定，进而从同一类样本中找出综合评价的最值，带入回归方程进行迭代，即可求出各项指标的允许变化范围。

2、模型的构建与求解

对L1～L5类项目进行分析，得到表6。

步骤3：求解各类项目风险度的最值maxFj和minFj；

表6 各类项目评价指标数据

步骤4：构建4项多元线性回归迭代方程：

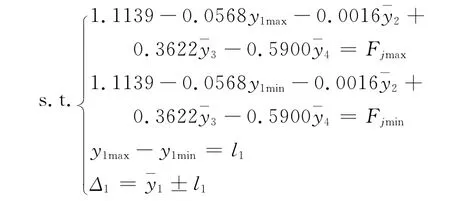
其中Δn，（n＝1，2，3，4）分别表示财务内部收益率、财务净现值、动态回收周期和收购储备面积的允许变化范围。

3、结果分析

通过选取不同类别的项目，分别进行多元线性回归拟合，得出相应的回归方程，进而计算出每类项目的指标允许变化范围，最后通过加权平均给出整个项目的评价指标允许变化范围，如表7。

表7 各指标允许变化范围

四、结语

针对3个有关土地储备项目风险问题，本文通过主成分分析法、Fuzzy AHP方法以及模糊偏差矩阵完善已有的风险评估方法，从而实现土地储备项目能够在较低风险的情况下取得最大的收益。随后，又通过模糊C均值聚类、多元线性回归等方法，给出了评价项目风险时各指标列的允许变化范围，从而明确了模型的适用范围，使得计量模型更加严谨而符合现实。本文运用多种软件给出各种相关图形，使人对数据的处理、模型的分析、结果的得出更形象易懂。文中的风险评估模型，能够对项目的风险进行一定的估算，可以为土地储备部门提供一定的参考。

［1］罗玲．基于土地可持续利用的我国城市土地储备投资可行性评价研究［D］．西安：长安大学（硕士学位论文），2007．

［2］任奎，周生路，张红富，等．城市土地储备规划风险评价研究——以南京市为例［J］．中国土地科学，2008（1）：59-65．

［3］陈晓军，盛淑凯，张建利，等．土地储备项目风险预警控制模型［J］．中国土地科学，2009（1）：38-42．

［4］林海明．对主成分分析法运用中十个问题的解析［J］．理论新探，2007（8）：16-19．

［5］周凯，宋凯军，邬学军．数学建模竞赛入门与提高［M］．杭州：浙江大学出版社，2012（1）：48-50．

［6］彭东黎，胡甜，郭云开．基于Fuzzy-AHP的膨胀土边坡稳定性多级综合评判［J］．中南大学学报，2014（2）：622-629．

［7］张焕明．统计学实验教程［M］．天津：天津大学出版社，2009．

［8］杨桂元，黄己立．数学建模［M］．合肥：中国科技大学出版社，2008．

［9］杨桂元，朱家明．数学建模竞赛优秀论文评析［M］．合肥：中国科技大学出版社，2013．

［10］李雷，罗红旗，丁亚丽．一种改进的模糊C均值聚类算法［J］．计算机技术与发展，2009（12）：71-74．

［11］高新波．FCM聚类算法中模糊加权指数m的优选方法［J］．模糊系统与数学，2005，19（1）：143-148．

［12］朱剑英．应用模糊数学方法的若干关键问题及处理方法［J］．模糊系统与数学，1992，11（2）：57-63．

［13］曹国钧．投资项目经济可行性综合评价数学模型及应用［J］．化工技术经济，2001（4）：32-37．