利用随机扰动特性的集合覆盖蚁群算法识别tag SNPs

王丽美，王龙香，郑程友（.临沧师范高等专科学校数理系，云南临沧677000；.福建农林大学计算机与信息学院，福建福州5000；.桂林理工大学机械与控制工程学院，广西桂林54000）

利用随机扰动特性的集合覆盖蚁群算法识别tag SNPs

王丽美1，王龙香2，郑程友3
（1.临沧师范高等专科学校数理系，云南临沧677000；2.福建农林大学计算机与信息学院，福建福州350002；3.桂林理工大学机械与控制工程学院，广西桂林541000）

序列中的标签SNPs-tag SNPs携带了SNPs数据集的绝大部分遗传信息，因此寻找tag SNPs意义重大.但从SNPs数据集中找出tag SNPs需要耗费巨大的计算量，传统的方法效率低且费用昂贵，对于复杂的集合覆盖问题，现有算法难以得到优化解.鉴于蚁群算法有较强的近优解搜索能力，提出具有随机扰动特性的集合覆盖蚁群算法（RCACO）用于tag SNPs搜索.模拟数据集上进行的算法实验结果表明，与近两年的PSO、GA两类算法相比，所提出的算法运行时间较短，搜索结果精确度更高.

tag SNPs；集合覆盖；蚁群算法；随机扰动

Wang LM,Wang LX,Zheng CY.A Collection of Random-Perturbation Characteristics Covered Ant Colony Algorithm to Identify TagSNPS[J].Journalof Yibin University,2015,15（6）：81-85.

全基因组关联性分析（Genome-Wide Associa⁃tion Study,GWAS）[1]是指在人类全基因组范围中找出单核苷酸多态性，从中挑选出与人类疾病相关的SNPs.SNP位点在药物基因组学、疾病基因定位和人群多样性的研究中发挥着及其重要的作用，是后基因组时代的重要研究课题.目前，很多的国内外学者已经在进行相关问题的研究，但是海量的数据与位点也给SNPs研究者们提出了巨大的挑战.生物信息学的快速发展的同时，越来越多的研究人员使用计算机相关方法对SNP数据利用概率与统计学的知识，找出与复杂疾病相关的SNP位点.

仿生优化算法是人工智能研究领域的一个很重要的分支，就是通过程序来模拟自然界已知的进化方法来进行优化的方法，比如模拟鸟类捕食的粒子群算法、模拟生物进化的遗传算法以及模拟蚂蚁觅食的蚁群算法等.从整体上来看，人类的智能远超越了其他生物的智能.鉴于人类生物系统的复杂性研究有极大的困难，将其他生物系统作为典型代表并加以探讨，可能在现阶段更具现实意义；同时作为人类生物系统复杂性研究的过渡阶段，其相关成果还具有拓广和延伸的价值.生物蚁群的行为规律研究可以集中显示群集智能涌现的特性，正因为如此，目前蚁群算法引起了专家学者的极大关注.

蚁群算法，是一种用来寻找优化路径的机率型算法.它由意大利学者Marco Dorigo于1992年在他的博士论文中首次提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为，其本质上是一个复杂的智能系统.蚁群算法是一种模拟进化算法，研究表明该算法具有许多优良的性质.目前，该研究已渗透到多个领域，并可解决多维的组合优化问题，这一新兴的仿生优化算法已成为交叉学科中人工智能领域的研究热点.

1　tag SNPs

1.1数据编码

高通量基因芯片技术迅猛发展，使得海量SNP数据可通过其进行基因分型，国际人类基因组单体型图计划（HapMap）为科学研究贡献了规模最大的SNP数据.构建人类DNA序列的多态位点常见模式是HapMap计划的最终目标，即单体型图[2-3].文章使用的SNP数据是经PHASE软件处理的HapMap的单体型数据.

HapMap的单体型数据中，每个SNP均是二等位的，即一个SNP是由A、C、G和T四个字母中任意两个字母表示的.为了便于机器学习方法的处理，对SNP的四个字母作了编码.编码的过程为：对每个SNP位点，分别统计表示它的两个字母在数据中出现的频率，将出现频率大的编码为1，将出现频率小的编码为0.

1.2tag SNPs获取

获取tag SNPs实际是在序列集中获取最小数目的SNP位点集SU，且在给定的位点集中均能满足上述两个特征的tag SNPs位点.描述如下：

输入：给定单体型序列集所对应的m*n矩阵M

输出：最小数目的tag SNPs位点集SU，且各tag SNPs位点需满足三点：

（2）任一tag SNP位点与其关联位点间的平均LD值应大于一定阈值（设定为0.6～0.8）；

标签SNP预测的目标是找出tag SNPs集，即H的最小最佳子集.引入了两个间接SNP位点集，候选集合L和目标集合B.集合L包含了所有符合作为标签SNP条件的SNP，集合B则包含了所有即将被选为标签SNP的位点，即集合L中的SNP与集合B中的标签SNP不存在连锁不平衡.对L中的每一个am，令C（am）={a：a∈B和r2（a,am）≥r0}代表B的子集，集合中均是与am具有强连锁不平衡的SNP，并令||C（am）为集合C（am）的元素个数.换句话说，候选集合L是tag SNP集合的替补集..

1.3实验数据集

随着生物学的不断发展，人类已经掌握成百上千万的SNP位点数据，其中部分数据可以从网上获取[4-6].下载HapMap（http：//www.hapmap.org）Encode数据库中的phased haplotype data.因为数据集是更新的，SNPs的数目在相同的区域中有点小差异.实验数据来自HapMap的4个编码区：编码区（STEAP，ENm010，ENm013，ENr113）数据收集于染色体7q21.13，2p16.3，4q26和5q31，分别包含25，105，376，523个SNP位点.其中STEAP来自于CEU种群，ENm010来自东京的日本种群，ENm013和ENr113来自于欧洲种群.在这四个序列集中来测试该算法的性能，并与近年来应用于tag SNPs的遗传算法（GA）及粒子群算法（PSO）的实验结果进行了比较.实验所得到的精确度预测值是基于tag SNPs位点预测非tag SNPs位点.聚类处理中所使用的数据集则是HapMap中YRI（尼日利亚伊巴丹）人种1号染色体所对应的单体型数据集（包括22 018个SNP位点构成的120条序列）.

2　集合覆盖蚁群思想

对集合覆盖问题的求解，已经有许多学者根据不同的思想提出了各种算法.比如，有基于分支定界思想来求解此问题的完整算法[7]，也有人通过对几种完整算法进行比较和分析，得出了针对于求解集合覆盖问题最好的完整算法[8].集合覆盖问题模型的应用非常广泛，目前优化集合覆盖问题主要采用的是一些近似算法，相对于复杂的或规模较大的数据集，传统算法因其运算时间太长，集合覆盖问题的优化效果不太理想.近几年，专家学者提出了启发式算法来求解此问题，利用启发式的优点，使集合覆盖的求解在可以接受的时间内得到近似最优解.

启发式的典型代表之一就是蚁群算法.蚁群算法主要是基于群体智能而得出的一种进化算法，它强调蚂蚁个体间的合作，利用信息素正反馈机制，较于其他智能算法具有较强的搜索较优解的能力.该算法从开始提出就受到了普遍关注，因其采用分布式并行计算机制，且易与其他机器学习方法结合，并且蚁群算法在很多复杂的组合优化问题领域已经有成功应用的例子，其出色的优化能力为本文优化集合覆盖问题提供了新的思路.

该算法同时也有消耗时间长和容易陷于局部最优解的缺陷.对蚁群算法作了深入的研究分析，并提出了基于罚函数的集合覆盖蚁群算法，将其命名为PCACO.主要内容是针对标准蚁群算法的不足做了改进，以此加强算法的优化能力，提高其收敛速度.用PCACO来优化集合覆盖问题，实验结果表明了PCACO求解集合覆盖问题在全局寻优及收敛速度上的优化效果理想.

3　具有随机扰动特性的集合覆盖蚁群算法（RCACO）

3.1算法的评估准则

目前，大多数文献中所使用的对tag SNPs位点选择算法的性能度量参数主要有三个：最终的tag SNPs位点数、算法运行时间及精确度值[5].在各个tag SNPs位点选择算法中，最后的tag SNPs位点数指的是算法最终结果中的SNP位点数；算法的运行时间则是从输入单体型数据开始直到算法终止所花费的时间；精确度值是用于衡量所tag SNPs位点所携带的信息量.

现已有若干种关于tag SNPs位点选择算法的精确度评估准则.两条单体型序列所有的SNP位点中相同位置所拥有的不同碱基对总数被定义为单体型的多样性，Clayton基于单体型的多样性提出了一种精确度评估标准.此方法能够定义一个tag SNPs位点集合是否可以有效地区分单体型，但它仅适用于有限多样性的单体型，面对单体型的大数据集却有失偏颇.之后，Stram[9]等人提出用关系质量度量r2来预测精确度.r2是tag SNPs位点预测得到的单体型数与所有SNP位点理论上的单体型数之间的一个关系度量，该度量标准适用于直接从基因型推导出的单体型.这两种评估标准均不适用于本文的算法，所以根据交叉验证的特点提出了新的评估标准.

为了提高算法的精确度，根据SNP位点的性质，提出了评估tag SNPs精度的公式，基本原理是基于获得的tag SNPs位点对其余非tag SNPs位点预测其精度.算法使用精确度（Accuracy，acc）和敏感性（Sensitivity，sen）[10]作为tag SNPs评估标准.

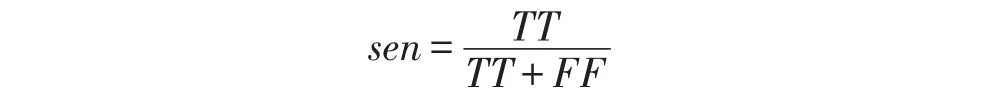
3.2RCACO算法原理及流程

基于罚函数的集合覆盖蚁群算法取得了良好的效果.结果表明，PCACO算法利用蚁群算法发现较好解的性质，优化了全局能力，且能够快速得到可行解，但最优解的精确度没有明显的大变化.针对此问题，提出另外一种改进方法：基于随机扰动特性的集合覆盖蚁群算法（RCACO）.

从ACO算法中的转移概率出发，经过深入分析后，提出了一种新的转移策略，即随机扰动的蚁群算法.新的转移概率具有自适应性和很强的扰动特性.RCACO主要包含两个方面的改进：一是设计了相应的随机选择策略和扰动策略；二是提出倒指数曲线所描述的扰动因子.实验表明：采用新转移概率的RCACO算法的精确度要高于PCACO算法，而计算时间差别不大，表现出了更好的全局搜索能力.除此之外，对RCACO算法中参数的选取方法和取值范围也进行了探讨.

从转移概率公式可以看出，ACO算法的主要依据就是信息素正反馈和启发因子的有机结合，基于此，采用了更为简洁的转移策略，公式如下：

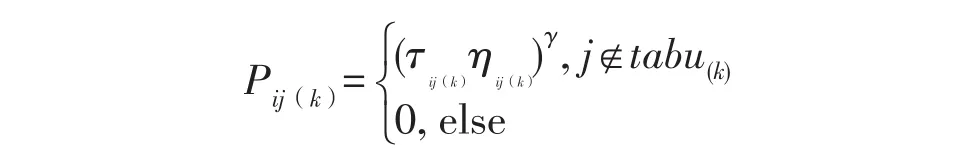
其中，γ为扰动因子，蚂蚁将选择转移概率最大的一条路径.值得注意的是，如果γ取固定值，仍会出现停滞现象，因此采用可变的扰动因子.扰动因子的取值要根据要考虑以下两个方面：

（1）蚂蚁总是选择转移概率最大的路径，当样本数目较大时，很难在短时间内找出一条较好的路径，所以在最初的迭代中，为了加速算法的收敛，我们同样应让γ取较大的值，才会使较好路径上的信息量高于其他路径.

（2）若γ一直不变必将导致随后的搜索出现停滞现象.因此，在之后的搜索过程中应适当减小γ的值，提高选择的多样性，即起到一定的扰动作用，其次也可使收敛走向平缓.

本文采用倒指数关系曲线来设置γ，公式如下：

γ=a×eb/k（k=1,2,…M）

其中，M表示最大迭代次数，a、b表示扰动尺度因子.为保证算法的随机性，随着迭代次数的逐渐增大，γ的值会慢慢接近系数a，且系数b的取值决定了曲线接近系数a的快慢.

为进一步缓解算法的局部停滞现象，在迭代过程中引入具有随机选择策略的动态转移概率.RCA⁃CO为了避免漏掉最优的一条路径，会对具有最大信息量的路径单独计算概率.所以，所设计的具有随机扰动特性的转移概率有以下四种情况：

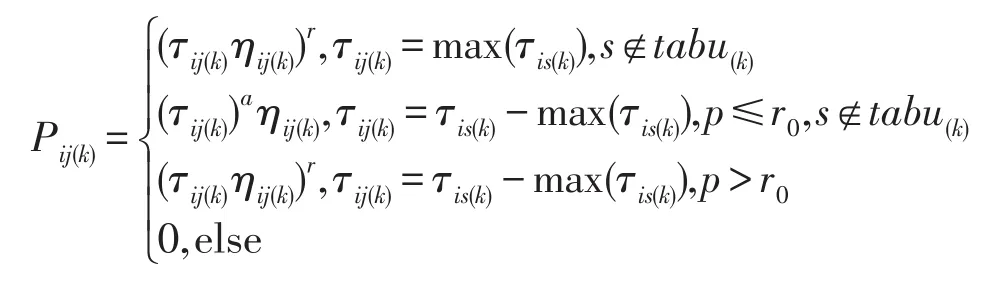
s=max（Pij（k））所对应的SNP位点集.

γ是具有倒指数性质的扰动因子；r0、p则都是（0，1）中均匀分布的随机数.转移概率公式表明，某只蚂蚁在迭代过程中可以选择多条路径，对于信息素浓度最大的路径，应选用p＞r0的公式，体现了其确定性；其它可选路径，则随机选择，这也导致了转移概率具有较强的随机性，该公式体现了确定性选择和随机选择相结合的形式，它们的共同作用使RCACO有更强的全局搜索能力.

3.3RCACO算法参数的选取

RCACO算法中，参数的选取对计算结果有很大的影响，算法所涉及的参数主要有α、ρ、Q、r0、a、b等.对于这些参数，并没有最佳组合，都是经验和具体问题试凑得来的.针对tag SNPs选取问题为例对RCACO进行了分析，通过大量的仿真实验确定了某些参数的最佳取值范围.

选取参数范围的步骤大致如下：

（1）实验发现，对算法影响较大的是α和Q，且相应的取值范围也较大.由于ρ和r0对算法的影响较小，取值一般较固定，介于（0-1）.因此，随机确定一组ρ和r0，接下来再调整α和Q，来获到较理想的解.

（2）在基本确定α和Q后，进行调整ρ和r0来寻找更优的解.得到稳定的结果后，将ρ和r0固定，再反过来调整α和Q值，如此反复，直到确定一组较为理想的参数组合.这种方法虽然繁琐，却效果明显，具有一定的普遍意义.

经此步骤，选取了以下参数的取值范围，在此范围时，算法可得到较好的解.

参数α表示信息量对蚂蚁选择路径的影响程度，参数Q的大小则决定了信息量的更新程度.此算法中，α的取值范围为0.1～0.5，Q本文取值为100.

ρ的取值不宜过小或过大.当ρ＜0.5，将不能很好地利用所积累的信息；当ρ＞0.8取值过大时，信息素密度则不能有效更新.ρ如果失去调节作用将导致会收敛于较差解，建议ρ的取值范围为0.5～0.8.r0作为决定信息素浓度的临界点，r0值的取值同样不能过小或过大，当r0＜0.3，则易丢掉路径较优的解，起不到该有的作用；当r0＞0.8，则容易陷入局部最优解，r0的取值范围为0.3～0.8.

（3）扰动尺度因子a的取值范围是1～10；b的取值范围为1～5，本文中（a,b）较优的组合有（3，2），（4，3），（5，2）.

4　仿真实验及结果分析

算法的终止条件是迭代次数达到1 000次，同时针对参数对算法性能的影响采用的是改变参数的策略，且每组数据实验30次取平均做比较.

采用1.3所表示的两个实验集，同时与GA、PSO 及PCACO三种方法进行比较.具体实验结果如下：

表1　仿真实验结果1（α=0.3，r0=0.7，ρ=0.6，（a,b）=（3,2））

表2　仿真实验结果2（α=0.4，r0=0.7，ρ=0.5，（a,b）=（4,3.2））

表3　仿真实验结果3（α=0.4，r0=0.8，ρ=0.6，（a,b）=（5,2））

由上面3个表1、2、3可明显看出，PCACO算法与RCACO算法的tag SNPs个数和运行时间均差别不大，但RCACO算法在精确度上却显著提高.

5　总结

特别针对标准蚁群算法中的转移概率进行了研究和探讨，并提出了一种新的转移策略，由此设计出一种随机扰动蚁群算法RCACO，将其应用在组合优化问题上.该转移概率带有一定的自适应性，并且具有很强的扰动特性.RCACO算法主要包含两个方面：一是提出了扰动因子，并采用倒指数曲线来描述；二是设计出相对应的扰动策略和随机选择策略.结果表明：这种新的转移概率可以有效地克服算法容易出现停滞现象的缺陷，拥有了更好的全局搜索能力；有效的提高了算法运算效率和计算精度.除此之外，该算法还对该算法中参数的选取方法及取值范围进行了研究.

[1]Klein RJ,Zeiss C,Chew EY,et al.Complement factor H polymor⁃phism in age-related macular generation[J].Science,2005,308 （5720）：385-389.

[2]Carlson C,EberleM A.Selectingamaximally informative setofsin⁃ gle-nucleotide polymorphisms for association analyses using link⁃age disequilibrium[J].Am JHum Genet,2004,74（1）：106-120.

[3]Phuong TM,Lin Z,Altman R B.Choosing SNPs using feature se⁃lection[C].Proc IEEEComputSystBioinform Conf,2005：301-309.

[4]Liu H,Motoda H.Feature selection forknowledge discovery and da⁃tamining[M].Boston：Kluwer Acdcemic Publishers,1998.

[5]WealeM.Selection and evaluation of tagging SNPs in the neuronalsodium-channel gene SCN1A：implications for linkage-disequilib⁃rium genemapping[J].Am JHum Genet,2003,73（3）：551-565.

[6]Stram D O,Leigh PC,Bretsky P,etal.Modeling and E-M estima⁃tion of haplotype specific relative risks from genotype data for a casecontrol study of unrelated individuals[J].Hum Heredity,2003, 55（4）：179-190.

[7]Youshikawa M,Amagasa T.Xrel：A path-based approach to stor⁃age and retrieval of XML documents using relational database[J].ACM Trans Internet Technology,2001.1（1）：110-141.

[8]Wen L,Zhang R,Lu X L.The design of efficient XML document model[C].Proceedings of the First International Conference on Ma⁃chine Leamingand Cybemetis,Beijing,2002：1102-1106.

[9]Dorigo M,Maniezzo V,Colorni A.Positive Feedback as a Search Strategy[M].Technical Report 91-016,Dip.Elettronica,Politeeni⁃co diMilano,1991.

[10]Dorigo M.Optimization,Learning,and Natural Algorithms（in Ital⁃ian）[D].Dip Elettronica,Politecnoco diMilano,1992.

（编校：许洁）

A Collection of Random-Perturbation Characteristics Covered Ant Colony Algorithm to Identify tag SNPs

WANG Limei1,WANG Longxiang2,ZHENGChengyou3
（1.Department ofMathematicsand Physics,Lincang Teachers'College,Lincang,Yunnan 677000,China；2.College ofComputerand Information Technology,Fujian Agriculture and Forestry University,Fuzhou,Fujian 350002,China；3.College ofMechanicsand Con⁃trol Engineering,Guilin University ofTechnology,Guilin,Guangxi541000,China）

Tag SNPs carriesmost of the genetic information of SNPs data set,which makes it significant to search tag SNPs.However,identifying tag SNPs from SNPs data set costs a huge amountof computation so that traditionalmethods are inefficientand expensive,and it turns difficult to obtain optimal solutions in case of complicated set cover problems.Since ant colony algorithms（ACO）work well in searching near-optimal solution,a new algorithm is proposed in searching tag SNPs,which combine setcoveringwith ACO based on random-perturbation（RCACO）.Experimental resultson simu⁃lated data sets show that the proposed algorithms achieve higher accuracy with less time consumption than PSO and GA algorithmsadopted in recentyears.

tag SNPs；setcover；antcolony algorithm；random-perturbation

TP301.6

A

1671-5365（2015）06-0081-05

2014-11-04修回：2014-12-09

王丽美（1987-），女，助教，硕士，研究方向为人工智能、数据挖据、生物信息

网络出版时间：2014-12-10 09：16网络出版地址：http：//www.cnki.net/kcms/detail/51.1630.Z.20141210.0916.004.html

引用格式：王丽美，王龙香，郑程友.利用随机扰动特性的集合覆盖蚁群算法识别tag SNPs[J].宜宾学院学报,2015,15（6）：81-85.