肿瘤病理类型绿色诊断方法研究——基于变精度粗糙集理论与贝叶斯网络

桑秀丽，李 哲，肖汉杰，吕 梁，王 华

（昆明理工大学 质量发展研究院，云南 昆明650093）

一、引 言

肿瘤的病理类型一直是国内外临床医学研究的重要内容之一。准确的肿瘤病理类型一方面有助于医师进行诊断，从而选择科学合理的诊疗方案，合理分配医疗资源，另一方面有助于减少患者精神和经济压力，提高患者满意度。

目前确定肿瘤性质和肿瘤病理类型主要依靠的方法有：医学影像学、超声诊断、放射性核素诊断、内镜诊断、肿瘤标志物诊断、组织切片诊断（“金标准”）等［1－2］。医学影像学主要是通过X光成像、CT、核磁共振成像（MRI）、超声成像等现代成像技术来对肿瘤的性质和病理类型进行确定［3］。组织切片诊断方法是病理检查的一种，用以检查机体器官、组织或细胞中病理改变的病理形态学方法。医学影像学是现代医学中最重要的临床诊断及治疗方法，但是最终诊断还是依赖医师临床经验，由于医生训练程度跟经验的丰富程度不同，对同一病症可能做出不同的诊断，容易造成误诊。虽然影像诊断方法简单易操作，但是存在较大的误诊风险，容易造成患者生命危险，引起医疗纠纷。如果影像诊断不明确时，最终都必须通过金标准检验，但金标准检验存在一定风险，价格较高且容易对患者身心产生重大影响，是诊断的最后选择。

随着医疗仪器设备的发展，医院能够采集的资料越来越丰富，可将越来越多的统计学方法运用到医疗诊断中。Hansen等使用对数线性模型与logistic回归模型对诊断方法进行了研究［4］；赵良渊等将多元线性回归模型在考虑共线影响点的情况下运用到医学中［5］；刘琼苏等将神经网络运用到乳腺肿瘤的诊断中，仿真结果表明其具有较高的准确性［6］；谢益辉运用R软件将分类与回归树应用到前列腺癌诊断中，得到了对疾病诊断和预防具有指导意义的结论［7］；孙静等将粗糙集理论引入到医学影像诊断中，通过与logistic回归对比，认为粗糙集有更高的预测精度［8］；王学伟将数据挖掘技术的贝叶斯网络运用到中医诊断中，通过交叉验证法得出基于关键症状诊断模型的性能相对基于全部症状的模型性能显著提高，贝叶斯网络适合解决诊断问题［9］。

有鉴于此，本文以昆明某医院常年肿瘤诊断报告为研究对象，提出了一种对病人无手术创伤，辅助医师进行诊断与推理于一体的肿瘤病理类型分析模型，即绿色诊断模型［10］。

肿瘤诊断过程中常常存在诊断信息的模糊性和不确定性［11］。模糊性是医学图像固有的特性，医学图像的部分容积效应跟医学图像的部分图像不能被准确分割，决定了医学图像具有模糊性，而医师的经验诊断主观性较大，使得诊断信息具有不确定性，有鉴于此，绿色诊断模型的诊断流程与理论方法具体为：

第一，对肿瘤数据运用粗糙集理论进行初步条件属性约简。

第二，建立病理类型诊断列联表，运用变精度粗糙集理论获得最小约简表。

第三，运用贝叶斯网络获得各病理类型发生的概率。

粗糙集是一种处理不确定性与模糊性的工具，简单实用是其特点，与数理统计方法相比，粗糙集对不完整与不确定性数据有较强的处理能力。与决策树算法、神经网络相比，粗糙集能够保证在分类能力不变的情况下，将专家知识约简，缩短学习周期，简化决策树，但是粗糙集的诊断推理速度受到简约得到的规则库大小的影响，且噪声易引起数据不一致性问题［12］。变精度粗糙集能够解决属性间无函数或不确定数据的分类问题，即对噪声数据具有免疫性［13］。贝叶斯网络具备学习和推理能力，且处理数据信息时具有柔和性、容错性的特点，此两种方法能够解决粗糙集出现的问题［14］。有鉴于此，本文提出了变精度粗糙集理论（VPRST）与贝叶斯网络（BN）相结合的方法来解决疾病诊断出现的问题。两种方法结合不仅能够克服各自对肿瘤诊断的不足，而且能够进行优势互补。实例证明，此组合方法在肿瘤诊断方面简单、准确、有效。

二、肿瘤病理类型绿色诊断模型

（一）肿瘤病理类型问题概述

肿瘤绿色诊断是指诊断设备、方法、过程不仅可以解决肿瘤病理类型诊断，还满足节省成本、保护环境、简单易操作的要求。肿瘤通常以组织发生为依据，每一类别又按其分化程度及其对机体影响的不同分为良性和恶性两大类。例如，甲状腺肿瘤可分为甲状腺良性肿瘤和甲状腺恶性肿瘤两类，甲状腺瘤良性肿瘤又分为甲状腺腺瘤、结节性甲状腺肿、亚急性甲状腺炎、甲状舌管囊肿；甲状腺恶性肿瘤又分为乳头状癌、滤泡状癌、未分化癌、髓样癌。

目前对肿瘤的诊断判别有辅助检查与鉴别诊断两种。以甲状腺肿瘤为例，辅助检查主要有甲状腺功能化验、核素扫描、B超检查、针吸涂片细胞学检查。鉴别诊断通过结节性甲状腺肿来判断肿瘤的良恶性，但是上述诊断只能对肿瘤良恶性做一个初步诊断，不能对所有病理类型做出判断。

（二）肿瘤病理分类诊断模型基本理论简介

1．变精度粗糙集简介

1993年Ziarko首次提出变精度粗糙集理论。变精度粗糙集是Z．Pawlak粗糙集的延伸与扩充，即当错误分辨率β＝0时，变精度粗糙集等于Pawlak粗糙集，Pawlak粗糙集是变精度粗糙集的一种特例［15］。

定义1：称c（X，Y）为集合X关于集合Y的相对错误分辨率，当且仅当满足如下条件

其中c（X，Y）×｜X｜称为绝对分类误差。

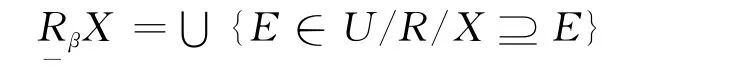
条件1：γ（P，Q，β）＝γ（red（P，Q，β），Q，β）。

条件2：red（P，Q，β）中属性不可再约简，即假设约简条件1不成立。

2．贝叶斯网络简介

贝叶斯网络是描述随机变量之间依赖关系的图形模式，被广泛用于不确定性问题的智能化化解［16］。它具有多功能性、有效性和开放性等特征，能够有效地转化数据为知识，并利用知识进行推理，以解决分析、预测和控制等方面的问题。

定义1：满足下面四个条件的有向无环图称为贝叶斯网络。

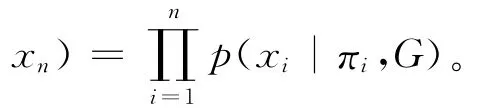
贝叶斯网络的构建可以分为以下三个步骤：

第一，明确变量与解释变量，以方便建模。

第二，独立条件的有向无环图的建立。由概率论相关知识可得到：

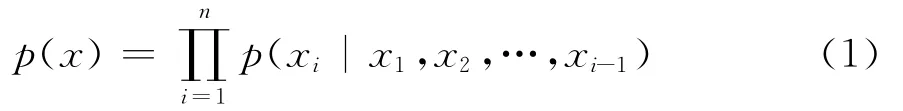
用Pai表示变量Xi的“因”，即父节点，则：

因此，首先需要通过对变量X1，X2，…，Xn排序，然后通过满足式（2）的父节点集Pai（i＝1，2，…，n）来决定贝叶斯网络的结构。

第三，指定局部概率分布p（xi｜Pai）。在离散的情形下，需要为每一个变量Xi的父节点集的各个状态指派一个分布。

3．建模步骤

具体建模步骤如图1所示。

图1 建模步骤图

三、构建肿瘤病理分类绿色诊断模型

本文以某三甲医院930例甲状腺肿瘤为例，首先将获得的甲状腺肿瘤的超声诊断数据通过粗糙集理论将条件属性进行初步约简，并运用改进的层次分析法对条件属性的重要度进行排名，然后运用变精度粗糙集理论获得调整后超声诊断症状（条件属性）与病理类型建立的关系集合R列表的最小属性集，最后利用贝叶斯网络既能进行“因→果”推理，又能进行“果→因”的逆向推理得到肿瘤病理类型的概率，概率最大的即为患者处于的病理类型［17］。

（一）构建肿瘤病理类型变精度粗糙集诊断模型

下面假设：U＝ ｛1，2，…，930｝，C＝ ｛b，c，d，e，f，g｝为条件属性，D＝ ｛a｝为决策属性。a＝ 肿瘤（良性 ＝1，恶性 ＝2）；b＝ 回声（低回声 ＝1，实性＝2，囊性＝3，混合＝4，等回声＝5，中等＝6，中低＝7，实质不均质＝8，无回声＝9）；c＝边界（清楚＝1，不清楚即毛糙＝2，成角＝3）；d＝形态（规整＝1，不规整＝2，凸向包膜外＝3）；e＝CDFI（短线状血流＝1，肿块内及周边见血流信号＝2，肿块内及周边血流丰富＝3，肿块内及周边未见血流信号＝4，环状血流 ＝5）；f＝肿块内斑点状强回声（钙化）（有 ＝1，无 ＝2）；g＝ 淋巴结肿大（有 ＝1，无 ＝2）。

通过计算，可以得到条件属性b，c，d，e，f，g的重要性分别为：

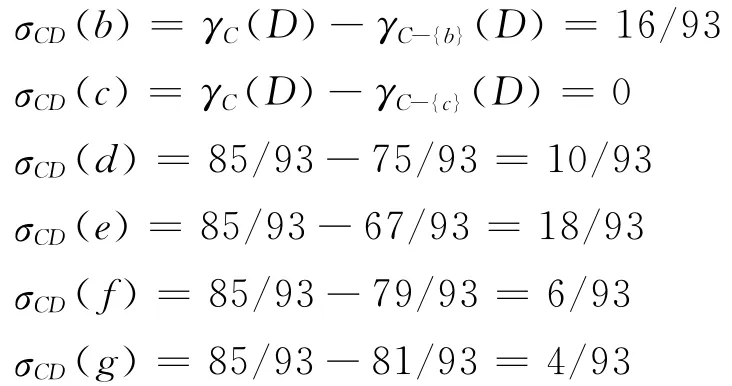
所以条件属性C的决策属性D约简为C－｛c｝＝｛b，d，e，f，g｝。

从上式可以得到重要度由低到高分别为e，b，d，f，g，c，其中c是冗余条件属性。下面用层次分析法对删除条件属性c的其他属性重要度进行修正。

由于层次分析法（AHP）的判断矩阵是由相对重要度组成，而由粗糙集得到的重要度是远远不够的［18］。基于此，本文提出利用粗糙集要度两两最简比四舍五入后的值作为相对重要度。假设在一个知识表达系统中C称为条件属性集，称为决策属性集，指标相对重要度定义如下：，其中ROUND代表四舍五入运算。

利用matlab得到判断矩阵的最大特征值λmax＝5．039 4，CR＝CI／RI＜0．10，即认为判断矩阵通过一致性检验。

最大特征值对应的特征向量即为重要度，从表1可以得到五个条件属性e，b，d，f，g的重要度分别为0．321 2，0．321 2，0．171 6，0．111 3，0．074 7，这说明判断肿瘤为良性或为恶性肿瘤先后顺序为CDFI、回声、形态、肿块内斑点状强回声、淋巴结肿大，其中CDFI、回声占的权重最大，为0．321 2。此时修正的粗糙集重要度只是给出了判断肿瘤的条件属性的优先顺序，但是哪些症状对应良性肿瘤与恶性肿瘤里哪个病理类型还需进一步分析。

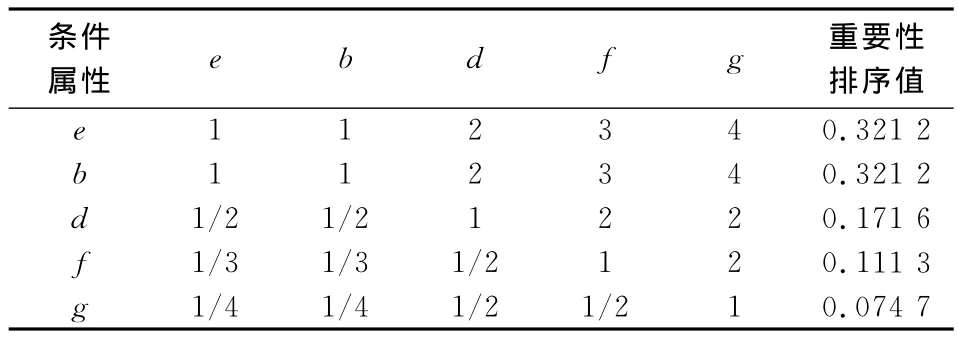
表1 判断矩阵表

表2给出了经过整理后的征兆集合M列表。表3给出甲状腺肿瘤病理类型N列表，其先验概率是利用历史资料计算得到的客观先验概率。

表2 超声症状集合M列表

表3 甲状腺肿瘤病理类型N列表

表4给出病理类型与甲状腺肿瘤分期之间的关系集合R列表，其中R列表中有缺失数据、噪声数据。

表4表示征兆与甲状腺肿瘤症状之间的关系，各概率值表示在ai发生的条件下mj发生的概率，用数学符号表示为

表4 征兆与甲状腺肿瘤症状之间的关系集合R列表

根据粗糙集诊断决策表，但表中数据为连续值，需要将其离散化。将表4中的数据离散化，规定量化为量化为1量化为2，其他的量化为3。条件属性取值3，2，1，0直观上可以理解为该病理类型引起此类型征兆的概率大、中、小、几乎没有。症状诊断决策表5如下，其中a7行表示噪声数据。

表5 症状诊断决策表

当β＝0．35时，正域为：

由以上得m4为核属性，逐一验证包含核属性值的所有情况，最后得到的近似约简有四个

删除结论属性对应条件属性为零的以及不确定属性值属性集，最终选择作为最小属性集，重新建立最小症状诊断决策表如表6所示。由症状与征兆之间的关系建立贝叶斯网络模型如图1所示，其中为父节点为子节点。

表6 最小症状诊断决策表

（二）基于贝叶斯网络的症状推理模型

贝叶斯网络利用一些征兆信息快速得出肿瘤症状发生的概率，便于对肿瘤进行诊断。据此构建如图2所示的推理模型：

图2 肿瘤诊断的贝叶斯网络模型图

具体计算步骤如下：

第二，各肿瘤症状发生的概率为先验概率与在其他条件下征兆发生概率的乘积，用概率公式表示为：

第三，在肿瘤诊断中，我们更希望得到哪个症状发生的概率最大，这样能有目的去做进一步诊断与治疗，即求

具体诊断步骤为：收集病人的征兆信息，得到征兆集中哪些征兆发生和哪些征兆不发生；根据已经得到的先验概率及在症状发生下的征兆条件概率，利用式（2）分别得到父节点a1，a2，…，a6发生的概率；将得到的概率按从小到大排序，概率最大对应的症状即为最有可能发生的症状。

例：某病人经超声检查具有单发结节，形态不规则，回声低而略欠均匀，伴砂粒样钙化，常侵犯周围组织，且淋巴结转移率最高，临床检查中降钙素的值常高于正常范围，声像图常表现为肿物后方回声不衰减的特点。

表7 各症状发生概率表

从表7可知，P（a3｜A＋∩A－）发生概率最大，即乳头状癌发生的概率最大，其次是结节性甲状腺肿和髓样癌，而实际情况是超声诊断为乳头状癌，诊断结论与实际情况吻合。

由上例可以看到，基于变精度粗糙集与贝叶斯网络的肿瘤病理类型诊断方法具有稳健性，其不仅可以对甲状腺肿瘤进行区分，还可以将其扩展到其他肿瘤领域。在实际运用中即使判断结果有误，也可以根据发生概率大小依次进行有方向、有目的的诊断，节省人力、物力、财力与时间。

四、肿瘤病理类型诊断结果分析与对比

根据贝叶斯网络模型，采用10折交叉验证法对数据进行测试，获得诊断的准确率、灵敏度、特异度，并以真阳性率（灵敏度）为纵坐标，假阳性率（1－特异度）为横坐标得到ROC面积。以上得到变精度粗糙集与贝叶斯网络模型的诊断性能与孙静的粗糙集方法进行对比，得到诊断性能对比表8。通过对比发现，变精度粗糙集与贝叶斯网络预测的精度高于粗糙集理论；ROC曲线AUG在90%以上说明它们都具有较高准确性，且VPRST与BN准确性更高一些；特异度都在90%以上反映筛检试验确定非病人的能力VPRST与BN比粗糙集理论更强；VPRST与BN比粗糙集理论有更高的灵敏度，反映正确判断病人的能力VPRST与BN比粗糙集理论更强一些。

表8 诊断性能对比表

五、结 论

肿瘤有良性与恶性之分，良性肿瘤对机体影响较小，恶性肿瘤由于分化不成熟、生长较快，浸润破坏器官的结构和功能，并可发生转移，因而对机体影响严重，因此准确对肿瘤进行诊断，尤其是恶性肿瘤的诊断对医院准确地了解病人情况，及时采取治疗措施具有重要意义。

肿瘤诊断常存在诊断信息的模糊性及信息缺失、噪声数据等引起的不确定性问题，使得目标识别与诊断变得困难。本文采用变精度粗糙集与贝叶斯网络相结合的方法对肿瘤症状进行诊断，该方法依托肿瘤诊断的历史数据，利用变精度粗糙集将专家知识简化，获得肿瘤诊断最小约简表。利用贝叶斯网络具有柔和性、容错性的特点，将最小约简表与贝叶斯网络结合，帮助医师根据病症识别患者肿瘤病理类型，进而采取更为科学合理的治疗方案。本方法将变精度粗糙集与贝叶斯网络结合，既发挥了变精度粗糙集处理模糊、不确定知识，对噪声数据有较强的免疫性能力，又发挥了贝叶斯网络的网络推理和诊断的能力，使得肿瘤诊断模型分别融合了变精度粗糙集与贝叶斯网络的优点，并且互相弥补了肿瘤诊断方法的缺点。

变精度粗糙集是一种定量分析的数学工具，将其运用到肿瘤诊断中，可以减少医生主观判断的偏误，而贝叶斯网络是为了解决不确定性、不完整性问题而提出，可以以概率形式更加形象具体地表征发生的可性，两者结合可以优势互补，实例对比分析证明此方法在肿瘤诊断方面的有效性、准确性。

［1］ 周纯武，赵心明，郝玉芝，等．医学影像学进展［J］．中国肿瘤，2008，17（9）．

［2］ Chantrain C F，DeClerck Y A，Groshen S，et al．Computerized Quantification of Tissue Vascularization Using High－resolution Slide Scanning of Whole Tumor Sections［J］．Journal of Histochemistry ＆Cytochemistry，2003，51（2）．

［3］ 高秀香，徐怡庄，赵梅仙，等．核磁共振波谱在肿瘤诊疗中的应用研究进展［J］．光谱学与光谱分析，2008，28（8）．

［4］ Hanson T E，Johnson W O，Gardner I A．Log－linear and Logistic Modeling of Dependence Among Diagnostic Tests［J］．Preventive Veterinary Medicine，2000，45（1）．

［5］ 赵良渊，何大卫，王彤．多元线性回归方程中共线影响点的诊断［J］．中国卫生统计，2004，21（2）．

［6］ 刘琼苏，何离庆．基于人工神经网络的乳腺癌诊断模型［J］．重庆大学学报：自然科学版，2003，26（4）．

［7］ 谢益辉．基于R软件rpart包的分类与回归树应用［J］．统计与信息论坛，2007，22（5）．

［8］ 孙静，孙兴旺．粗糙集方法在医学影像诊断分析中的应用［J］．统计与信息论坛，2012，27（6）．

［9］ 王学伟，瞿海斌，王阶．一种基于数据挖掘的中医定量诊断方法［J］．北京中医药大学学报，2005，28（1）．

［10］Gotwald T F，Daniaux M，Stoeger A，et al．The Value of the World Wide Web for Tele－education in Radiology［J］．Journal of Telemedicine and Telecare，2000，6（1）．

［11］龚燕冰，倪青，王永炎．中医证候研究的现代方法学述评（二）——中医证候的量化及数理统计方法［J］．北京中医药大学学报，2007，30（1）．

［12］张爽，刘雪华，靳强．决策树学习方法应用于生态景观分类［J］．清华大学学报，2006，46（9）．

［13］徐红升，张瑞玲．变精度粗糙集在智能诊疗系统中的应用［J］．计算机应用与软件，2013，30（2）．

［14］张娜，王国永，朱晓艳，等．贝叶斯网络在艾滋病发病影响因素研究中的应用［J］．中华预防医学杂志，2014，48（4）．

［15］Pawlak Z．Rough Sets［J］．International Journal of Computer ＆Information Sciences，1982，11（5）．

［16］黄影平．贝叶斯网络发展及其应用综述［J］．北京理工大学学报，2013，33（12）．

［17］宋永涛，苏秦．基于贝叶斯网络的质量管理实践对绩效的影响评价［J］．系统工程理论与实践，2011，31（8）．

［18］Saaty T L．A Scaling Method for Priorities in Hierarchical Structures［J］．Journal of Mathematical Psychology，1977（3）．