基于模式识别理论的卡钻类型判别分析

吴 军，臧艳彬，陈星星

(1．中国石化重庆涪陵页岩气勘探开发有限公司，重庆408014;2．中国石化石油工程技术研究院，北京100101)

作为人工智能技术基础学科的模式识别技术，在文字识别、遥感、气象预报、军事侦察等领域都取得了巨大成效。模式识别自20世纪60年代发展成为一门独立学科以来，共经历了2个阶段:统计模式阶段和人工智能阶段。统计模式识别方法主要有判别函数法、k近邻分类法、Bayes判别法、主因子分析法等，其中Bayes判别规则从理论上解决了最优分类器的设计问题。90年代统计推断理论研究所取得的突破性成果促成现代统计学习(VC)理论的建立，该理论不仅在严格的数学基础上圆满地回答了人工神经网络中出现的理论问题，而且导出了一种新的学习方法——支撑向量机，从而将模式识别技术推向另一个高峰［1］。

卡钻是钻井施工过程中最常见和易发的事故之一，卡钻事故的影响因素多种多样且关系复杂，传统的统计分析和摩阻系数方法预测效果不理想。目前卡钻预测与判别技术尚没有实质性的突破。卡钻的钻前预测与预防主要依靠工程技术人员的操作经验和相关技术规范进行，预测精度较低。本文以近几年中石化四川盆地川东北地区(元坝、普光等气田)卡钻资料为样本，采用支持向量机方法进行了卡钻判别分析，建立了卡钻类型判别方程，并分别与Bayes判别法和多元回归分析的预测结果进行了对比。计算结果表明，利用模式识别理论建立的卡钻类型判别模型进行卡钻的预测和评估是切实可行的［2－8］。

1 模式识别理论

1．1 多元回归

假定被解释变量Y与多个解释变量X1，X2，…，Xk之间具有线性关系，是解释变量的多元线性函数，称为多元线性回归模型［9］。即

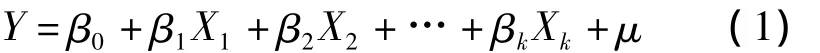
其中Y为被解释变量，Xj(j=1，2，…，k)为 k个解释变量，βj(j=0，1，2，…，k)为 k+1 个未知参数，μ为随机误差项。

1．2 Bayes判别法

设G1，G2，…，Gk为k个p元总体，分别具有概率密度 f1(x)，f2(x)，…，fk(x)，在进行判别分析以前，我们已对各总体有一定的了解。一般说来，一个待判样品应该首先考虑判入有较大可能出现的总体之中［10］。在Bayes判别中，应该考虑误判引起的损失。

此时的Bayes判别法则:

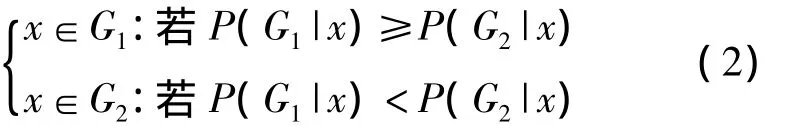
Bayes判别(即使L达到最小)的最优划分为:

1．3 支持向量机(SVM)判别法

支持向量机是V．Vipnik等根据统计学理论(Statistical Learning Theory简称SLT)提出的一种新的机器学习方法，在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势［8］。支持向量机从本质上讲是一种前向神经网络，通过核函数将实际问题转换到高维特征空间，并在高维特征空间中构造线性判别函数来实现原空间中的非线性判别函数。从实施的角度考虑，训练支持向量机的核心思想等价于求解一个线性约束的二次规划问题，从而构造一个超平面作为决策平面，使得特征空间中两类模式之间的距离最大，而且它能保证得到的解为全局最优解［11］。

设线性可分样本集为(xi，yi)，i=1，2，…，n，x∈Rd，y∈{+1，－1}是类别标号。d维空间中线性判别函数的一般形式为:g(x)=w·x+b，分类面方程为:

将判别函数进行归一化，使两类所有样本都满足|g(x)|≥1，即，使离分类面最近的样本|g(x)|=1，这样分类间隔就等于2/||w||，因此间隔最大等价于使||w||(或||w||2)最小。而要求分类线对所有样本正确分类，就是要求其满足:

因此，满足上述条件且使||w||2最小的分类面就是最优分类面。这两类样本中离分类面最近的点且平行于最优分类面的超平面上的训练样本就是使

式(4)中等号成立的那些样本，即支持向量(Support Vectors)。根据上面的讨论，最优分类面问题可以表示成如下的约束优化问题，即在式(4)的约束下，求式(5)的最小值。

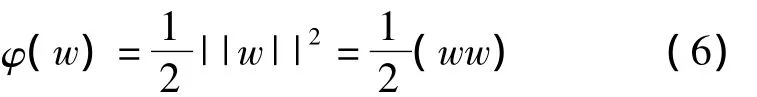
这是一个二次规划问题，可定义以下的拉格朗日(Lagrange)函数:

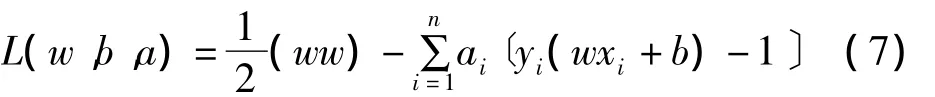
其中:ai＞0为Lagrange系数。求式(8)的极小值就是对w和b求拉氏函数的极小值。求L对w和b的偏微分，并令其等于0，可转化为对偶问题。

如果用内积K(x，x’)代替最优分类面中的点积，就相当于把原特征空间变换到了某一新的特征空间，此时优化函数变为:

相应的判别函数也应变为:

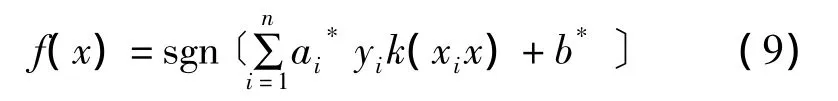
常用的核函数有以下几种:

线性内积函数K(x，y)=xy;

多项式内积函数K(x，y)=(xy+1)d;

径向基内积函数K(x，y)=exp(－|x－y|2/σ2);

二层神经网络内积函数K(x，y)=tanh〔k(xy)+c〕。

2 卡钻判别结果分析

为了对比分析3种判别方法，整理了中石化川东北地区(元坝、普光等气田)卡钻事故相关数据，这些参数包括影响卡钻的主要参数，如地层参数、钻井液性能参数及井径扩大率的工艺参数。

2．1 数据预处理

参照现场数据，按照支持向量机、Bayes判别法和多元回归分析建模要求，将所需数据作如下预处理:卡钻类型按坍塌卡钻、压差卡钻、缩径卡钻、沉沙卡钻、键槽卡钻、其他卡钻、正常钻进分类卡钻类型值分别为(1，2，3，4，5，6，7);此次研究共搜集样本52条，见表1。

2．2 计算公式

(1)利用多元回归分析算法求出卡钻类型值与影响因素的关系式为:

表1 卡钻类型判别样本

上式中的残余方差为340．058，多重相关系数为0．662，拟合精度较低。

(2)采用Bayes判别分析法求得卡钻类型值与影响因素的关系为:

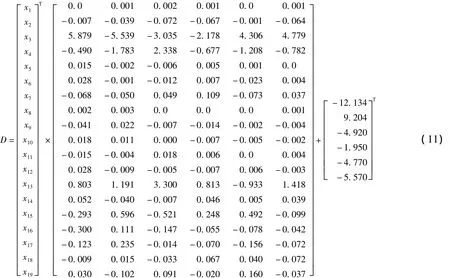
(3)采用支持向量机(SVM)计算出卡钻类别值公式为:

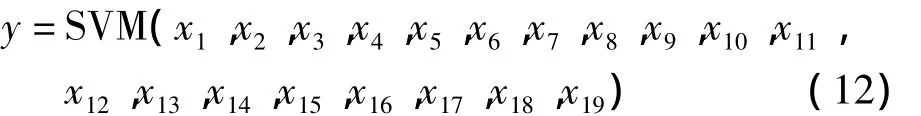
其中SVM是非线性函数，这种函数可以用显式的数学形式表示，故称为“显式”表达式。SVM卡钻类型判别结果如图1所示。

2．3 算法结果对比分析

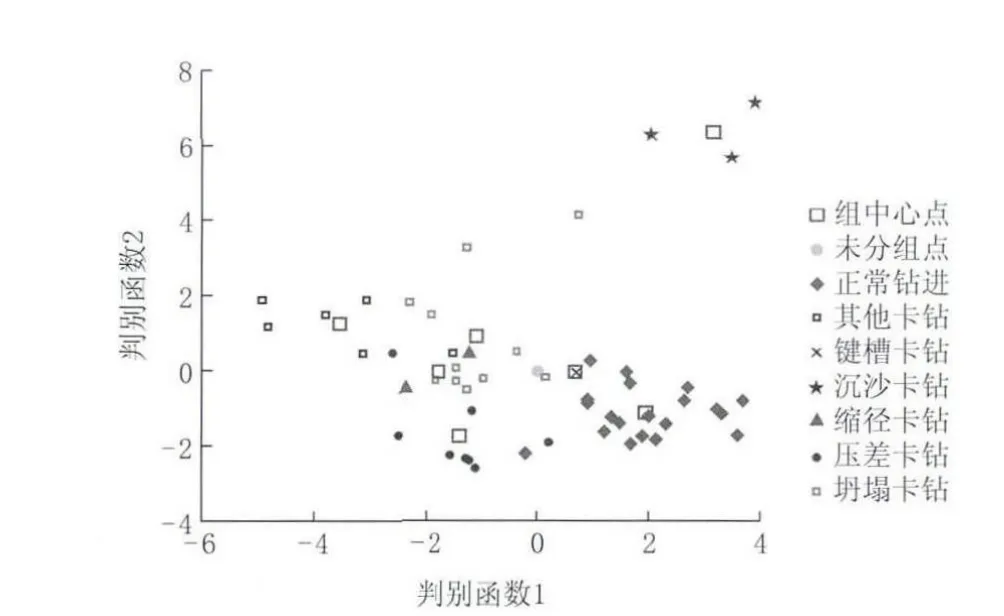
图1 SVM卡钻类型判别分析结果

以中石化川东北地区(元坝、普光等气田)近几年发生卡钻事故案例为样本，分别采用多元回归分析、Bayes判别分析、支持向量机进行卡钻类型判别分析，其预测结果见表2。

表2 3种算法预测结果对比

将3种算法对卡钻故障预测结果对比(见表3)，可以看出其优劣排序为支持向量机＞Bayes判别法＞多元回归分析。卡钻判别实例表明，支持向量机作为一种非线性算法远比后两种线性算法优越。其根本原因在于卡钻类型的影响参数与卡钻类型存在复杂的非线性关系。另外，Bayes判别法也具有简明、快速的优点，其精度高于多元回归分析，而多元回归分析不仅计算速度快，而且具有能表达研究目标与其相关因素之间亲疏关系的优点，可作为辅助手段。

表3 3种算法综合评价

3 结论与建议

(1)卡钻应用实例表明，基于模式识别理论的支持向量机和Bayes判别法与多元回归分析相比，对卡钻类型识别准确率更高，特别是基于计算机机械学理论的支持向量机(SVM)模式识别方法，对卡钻类型的识别率达到98．08%。

(2)将计算机模式识别理论应用于钻井工程中卡钻判别分析，取得了较好的识别效果，所建立的判别方程式具有卡钻类型判别功能，从而为卡钻类型分析与技术措施的制定提供指导意见。

(3)实际应用中可选择其中的1～2种进行联合判别。本研究为卡钻类型的定量判别提供了一种新的研究思路，对现场卡钻事故的预防与处理具有一定借鉴和参考价值。

［1］ 边肇祺，张学工．模式识别(第二版)［M］．北京:清华大学出版社，2007:32－51．

［2］ 阎铁，毕雪亮，王长江．基于支持向量机和聚类分析理论的钻具失效分析方法［J］．石油学报，2007，28(3):135 －140．

［3］ 石广仁．支持向量机在多地质因素分析中的应用［J］．石油学报，2008，29(2):195 －199．

［4］ 李建军，丁正生，张海燕．常用判别分类方法分析［J］．西安科技大学学报，2007，27(1):138 －142．

［5］ 罗刚，艾志久，王其华，等．基于模糊数学卡钻事故安全评价体系研究［J］．西南石油大学学报，2007，29(6):118 －122．

［6］ 陈晖，沈小翠．卡钻事故诊断仿真系统研究［J］．石油机械，2009，37(7):55 －57．

［7］ 张林强．井下卡钻分析及处理［J］．海洋石油，2007，(3):112－116．

［8］ Vapnik V N．The nature of statistical learning theory［M］．Translated by zhangxuegong．Bejing:Tsinghua University Press，2000:85 －205．

［9］ 严丽，王燕，范树平．多元回归分析方法预测川东北礁滩相储层产能［J］．新疆石油天然气，2011，7(4):37 －40．

［10］ 顾和元，侯国庆，吴占伟．基于动态贝叶斯网络的深水防喷器可靠性研究［J］．石油机械，2013，41(3):36 －39．

［11］ 韦明辉，黄海龙，韦忠良，等．基于支持向量机的钻井风险实时预测方法［J］．钻采工艺，2012，35(5):15 －17．