水锤效应影响洗井效果的原理

吕 健，刘盈君，杨甘生

(中国地质大学〈北京〉科学钻探国家专业实验室，北京100083)

0 引言

在水文勘探孔和供水井的钻进过程中，从钻头破碎井底岩石的瞬间开始，泥浆中的自由水和固相颗粒以及高聚物就不断向地层孔隙中渗透形成泥皮。随着渗透的不断进行，泥皮的厚度也不断增加。泥皮的存在虽然会平衡地层压力，减缓泥浆的漏失，但也会影响水文勘探孔的钻孔涌水量和单位涌水量，以及通过抽水试验数据计算而得到的相关水文地质参数。所以，洗井效果的好坏是水文勘探孔和供水井能否顺利成井的关键。据不完全统计，现有的洗井方法有上百种，但常用的主要是活塞洗井法、抽水洗井法、空压机洗井法、震荡洗井法、二氧化碳洗井法、喷嘴反冲洗井法、抽筒洗井法等。

洗井的主要目的是破坏钻进过程中在孔壁上形成的泥皮，消除渗入含水层中的岩粉与泥浆，同时要使滤料和靠近滤料的含水层中的颗粒按其大小重新排列组合，以形成良好的人工过滤层［1］。泥浆中的细颗粒在钻进过程中仅瞬时滤失过程就可以渗入地层25～30 mm，如果洗井工艺在水井下管和填砾后不能及时进行，停放时间过久，泥皮会发生硬化，给利用物理方法的洗井工艺如抽水洗井法带来极大的困难。本文将针对洗井过程中水锤效应对泥皮的破坏原理进行简单的讨论，希望能起到抛砖引玉的作用。

1 洗井中的水锤效应

封闭洗井、振荡洗井、活塞洗井以及其他各种洗井方法中都广泛存在着水锤效应。水锤是管道瞬变流动中的一种压强波，它是由于管道中某一截面的流速发生了改变，从而使该处压强产生一个突然的跃升或下降［2］。水锤效应引起的压强升高，有时是非常大的，可能引起管路爆裂;水锤引起的压强降低，管内形成真空，有可能使管路扁缩而损坏。一般钢管的水锤波传播速度大约在1000 m/s，若管内液体流速为3～4 m/s，则突然关阀引起的水锤压强约为3～4 MPa［2］。因此，在洗井过程中我们可以充分利用水锤效应造成的强大压强破坏泥皮，以达到良好的洗井效果。

在一般的抽水洗井过程中，由于开泵瞬间井管中的水被突然抽出，造成井内水位突然下降，使得含水层与井管内出现较大的水头差，水头差的存在为冲刷和破坏井壁上的泥皮提供了原动力。随着抽水过程的不断进行，含水层中的水位也逐渐减低形成下降漏斗［1］，如图1所示。实际上，冲刷破坏泥皮的原动力主要由2部分组成:一是宏观上由于抽水造成井内水位下降，形成的水头差;二是开泵停泵的瞬间由于流速突然改变造成的水锤压强。振荡洗井就是利用开泵停泵瞬间在井内产生巨大的水锤压强，反复冲击破坏泥皮，以沟通含水层和井壁的连通性，达到良好的洗井效果的。而封闭分段洗井则是在振荡洗井的基础上，利用PACKER将水泵或空压机混合器的两端封隔，通过减小洗井段的长度来增强破坏泥皮的效果。其中，封闭反压洗井通过空压机反压给予地下水更大的流速变化值，更加充分的利用了水锤效应。活塞洗井也是依靠上下拉压活塞，造成压力的跃升和下降，从而改变水流速度，产生水锤压强。整个活塞洗井过程亦可以看作是个封闭段较长的封闭反压洗井。

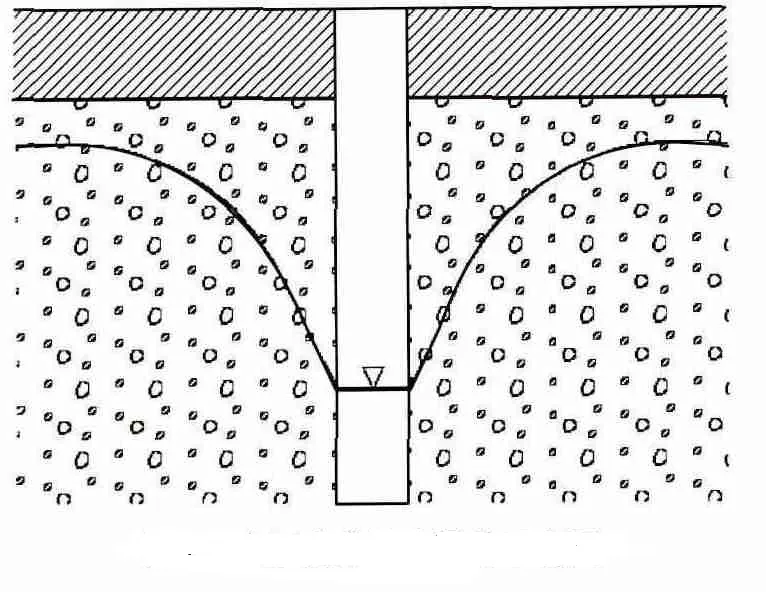
图1 水泵洗井抽水漏斗示意图

2 水锤效应洗井原理

水锤效应是流体在管路中非定常流动的一个特例。在洗井的过程中，水锤效应主要出现在开机和停机的瞬间。为了更好的介绍洗井过程中的水锤效应，现以封闭反压洗井法为例进行原理分析。

2．1 水锤效应的形成过程

封闭反压洗井法曾于1979年在陕南江汉北岸二级阶地后缘某厂供水井中被使用。该井活塞洗井后先用空压机洗井10个台班，后改用封闭反压洗井法重新洗井5个台班，使该井单位涌水量增大5．7倍［1］。其工作原理示意如图2所示，在泵(或空压机混合器)的两端添加两个封隔器(或海带止水)形成一个封隔段，空压机通过风管向封隔段加压时，井筒中的水被迫向含水层中流去;空压机突然泄压后，它们又在压力的作用下重新返回到井筒中甚至是喷出地表。空压机加压泄压的过程中，地下水的流速随之不断改变，因而产生水锤压强破坏泥皮。若在该封隔段内反复振荡洗井，就可达到良好的洗井效果。

假设风管无限靠近上封隔器，且看作是个可以开闭的阀门，则空压机泄压表示阀门开启，地下水通过井管喷出地表;加压表示阀门关闭，地下水停止流动或被迫向含水层中流动。将井管封隔段平均分为无数个厚度为Δh的液层。取无限靠近上封隔器的m－n段为研究对象，如图3所示。当阀门突然关闭时，在无限小的时间Δt内，紧靠上封隔器下端的m－n段首先停止运动，此时紧挨m－n段底部的水由于惯性作用仍以速度v0向上运动，因此对m－n段产生挤压作用，致使其发生弹性形变［3］。由弹性模量的计算式可知，应变与应力成正比。则m－n段受到压缩后其应力会相应增大，这个增大的应力称为水锤压强。

图2 封闭反压洗井示意图

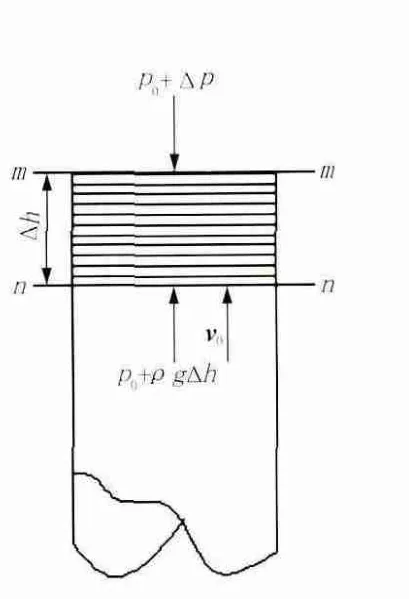
图3 水锤压力导出示意图

m－n段停止运动以后，接着下部各层地下水也相继停止下来，这样一层复一层被停止的结果是每一层水都受到下一层水的挤压作用，最终动能全都转变为弹性势能，各层水依次产生水锤压强。因而在地层中形成了靠近上封隔器的高压高能区和靠近下封隔器的低压低能区。当高压高能区弹性势能积蓄到最高值后，能量开始向低压低能区释放，地下水又从上至下依次开始向下运动。下部低压区的地下水逐渐受到压缩，继而动能转变成弹性势能成为高压高能区，上部的高压高能区段则由于地下水的流出逐渐解压成为低压低能区。下部高压高能区弹性势能积蓄到最高值后，地下水又开始向上压缩。至此，水锤的传播完成一个周期，若不考虑能量损失，水锤将无限循环传播下去。理想情况下m－n截面上水锤压强随时间变化如图4所示。可以看出，水锤效应所产生的水锤压强，正像弹簧伸缩一样可看作是个以阀门为振源，将机械能和弹性势能相互转化的纵波，称为水锤波。在沿水锤波传播方向上有疏部和密部之分。

图4 理想水锤压强时间变化图

2．2 水锤压力值的推算

为了更好的计算在加压和泄压瞬间水锤压强的大小，现做以下简化与假设:

(1)假设井孔一径到底，无超径、缩径现象;

(2)假设地下水在含水层和井管中运动时无不计摩擦阻力和粘性阻力做功;

(3)假设空压机的加压、泄压过程为一维不定常流动，且在极短时间内完成;

(4)假设空压机风管为可开闭的阀门，且无限靠近上封隔器。

参照《工程流体力学》中对水平管道中水锤压强的推算，可对竖直井管中的水锤压强进行推算［3］。以p0表示阀门尚未关闭时截面m－m的压强，则截面m－m关闭阀门后的压强为p0+Δp，截面n－n阀门关闭瞬间的压强为p0－ρgΔh。由此可知，m－n段在压缩过程中所受外力为:

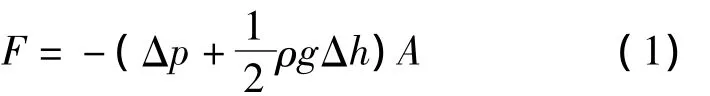
式中:Δp——压强的改变值;ρ——地下水的密度;g——重力加速度;Δh——位置水头改变值;A——m－n段的横截面积。

m－n段在时间Δt内的动量改变了－ρAΔhv0，由动量定理可知:

即:

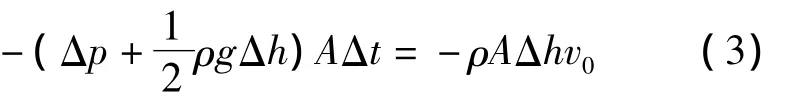
整理可得:

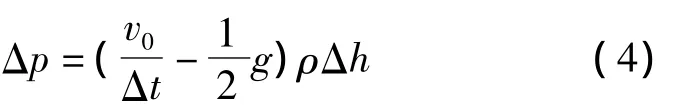
式中:v0——水的流动速度。

由于阀门的关闭是在极短时间内完成的，即Δt的值无限小，v0/(Δt)的值无限大且v0/(Δt)(1/2)g，即可以不考虑重力竖直方向的作用，则式(3)可进一步简化为:

令C=Δh/Δt表示水锤压强波的传播速度，水锤压力可表示为:

水锤压强波传播速度公式是由俄国人儒可夫斯基推出的:

因此，封闭反压洗井中水锤压力的大小公式为:

为推动食品安全城市创建工作，仓山区局牵头制定《食品安全城市创建工作方案》，列明全区各责任单位的10大项99小项工作要求，大胆探索社会共治，将创建工作纳入街道绩效考评的“街道共建”模式和在市场中引入业主责任制及第三方监管机制的“新西营里市场”模式，新西营里市场获评“全国诚信示范市场”。

式中:ρ——水的密度，取 ρ=1.0 ×103kg/m3;v0——地下水在井管中的流速，m/s;E0——地下水的弹性模量，取 E0=2.058 GPa;D——井管直径，mm;e——井管的厚度，mm;E——井管弹性模量，GPa。

一般情况下，水文地质勘探孔的井径在130～250 mm，水井的井径在300～500 mm。现假设井管直径D=225 mm，壁厚e=25 mm，地下水流速v0=1 m/s，井管材料为铸铁，由表1可知E=196 GPa。

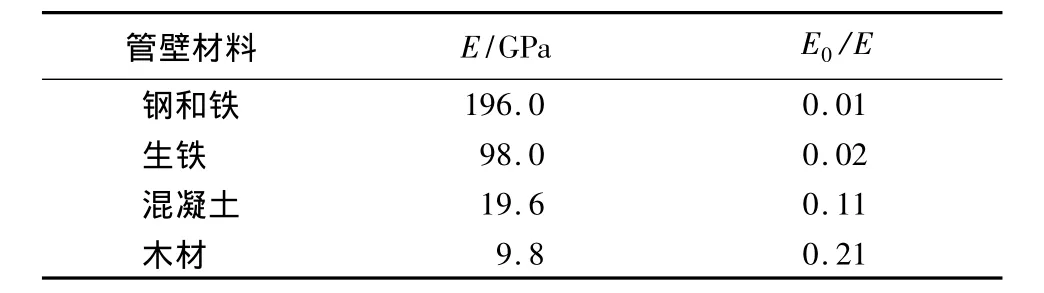
表1 各种管壁材料的弹性模量［3］

将以上数值代入式(8)中，可得到水锤效应在井管中产生的压力的粗略值:

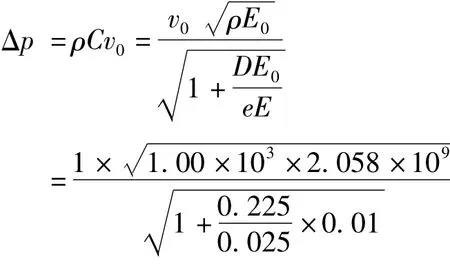
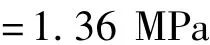
即在以上假设条件下，阀门突然关闭时水锤效应在井管管壁上所产生的压强可达到1．36 MPa，相当于136 m的水头差，远远大于一般抽水时的降深。故水锤压强在洗井中起到了重要的作用。

3 水锤效应洗井方法的优化

研究水锤效应影响洗井效果目的之一是更加充分的利用水锤压强，更加合理的设计洗井方案。通过对水锤效应在井管中传播过程的分析以及水锤压强的推算，可以从以下2个方面对洗井方案进行优化。

3．1 提高流速v0

在确定的井孔中，井管直径D、井管壁厚e和井管材料(即井管弹性模量E)为不能改变的确定值。分析水锤压强的公式可以发现，通过提高地下水在井管内的流速v0来增大水锤压强。

(1)封隔段长度L和泵的流量Q都不变时，可以通过将泵口放置在封隔段的一端来增大流速。当泵口放置在封隔段一端时，泵的流量可以用下式表示:

故:

即当泵口位于封隔段的一端时，封隔段内任意一点的平均流速要大于泵口在其它位置时该点的平均流速。实际抽水洗井中为防止掉泵，泵口位置一般选择放在封隔段最底端。

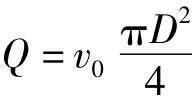
3．2 利用波的性质

前文已经讲到，水锤波是个以阀门为振源，将机械能和弹性势能相互转化的做简谐运动的纵波。仍以m－n段为研究对象，当m－n段停止运动后，下层水由于惯性仍以速度v0向上流动，使m－n段受到挤压发生弹性变形，弹性变形包括轴向的压缩和径向的扩张。由于水是各项均匀的介质，故在水锤波既在井管轴向上传播也在径向上传播，且径向扩张与轴向压缩具有一样的周期性，即水锤波的周期T。

为了得到水锤波的周期，我们暂且将水锤波在轴向上的振动简化成如图5所示的弹簧振子的振动，封隔段内水的质简化成其质心位置(L/2处)处的小球，由弹簧振子串联性质可得到劲度系数［4］:

式中，k1、k2——分别为弹簧振子的进度系数。

此处k1=k2=E0，整理得k=E0/2。

因此可得到周期为:

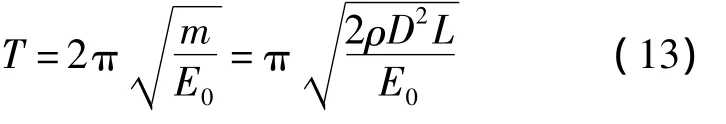
式中:m——封隔段水的质量，kg;D——井管直径，m;L——封隔段长度，m;E0——水的弹性模量，GPa。

由此可以得到水锤波的波长为:

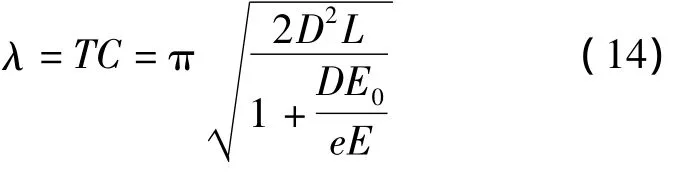
若取封隔段长度 L=20 m，D=0.225 m，e=0.025 m，E=196 GPa，则代入式(14)可算得波长λ≈5.83 m。

洗井过程中，封隔段的位置均是选在滤水管的位置。滤水管上的过滤器一般为圆孔或直缝，其直径或宽度范围在几毫米或十几毫米内，远远小于水锤波的波长。因此，水锤在径向上的波动透过滤水管上成排的过滤器时会发生衍射和干涉现象，如图6所示。

图5 水锤波简化图

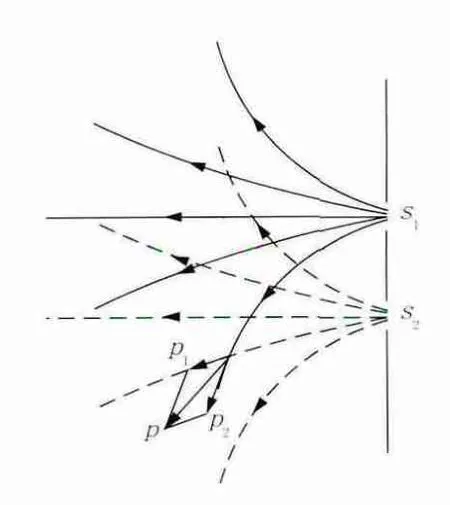
图6 纵波干涉示意图

根据纵波干涉的规律可知两个相干波源干涉时，相交点的振幅是两相干波源的矢量相加，若以压强P表示振幅，则有:

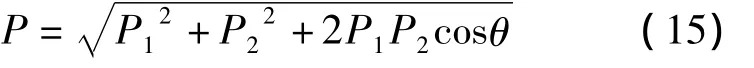
由式(15)可以得知，干涉水锤压强的大小与相关振源的振幅P1、P2以及cosθ的值有关。

当cosθ的值固定不变时，S1、S2相位相同，则P1、P2在同一时刻达到最大值，则P也取得最大值。取S1、S2的间距为md，若相位相同则要求:

整理可得:

式中:φ——相位差;λ——水锤波波长;m——滤缝个数;d——滤缝间距。

在既定的滤水管中，任意两个滤缝间距为md。当两相关波源相位差φ恒定即n为固定的某个整数时，md随着波长λ减小而减小。因此，在滤水管单位长度范围内，S1、S2间距md减小，但数量增多。即相关波源的密度增大，干涉加强点的密度也随之增大。

由波长公式式(14)可知波长λ与封隔段长度L成正相关，减小封隔段长度即可达到减小波长，增大最大干涉压强密度的目的。与此同时，从式(13)可以发现，封隔段长度L与周期T亦成正相关，L减小后T也会变小，最大干涉压强出现的频率也相应提高。

综上所述，要增大水锤压强，可将泵的入水口放在封隔段最底端、提高泵量和减小封隔段长度3种方法实现。同时，水锤效应在弹性模量较大的铸铁管、井管直径与壁厚比较小，以及填砾厚度适中的井中洗井效果更佳。

4 结论

(1)水锤效应广泛存在于洗井方法中，尤其在封闭分段洗井和活塞洗井中效果良好。

(2)经过相应假设条件下的推算，水锤压强产生的水头差可高达136 m，远远大于由于抽水形成的降深值，为水锤压强良好的洗井效果提供了理论依据。

(3)为了更加充分合理的利用水锤效应，可以通过提高泵量Q或将泵的入水口放在封隔段的最底端来实现。

(4)可以通过减小封隔段长度L缩短水锤波的周期T，提高最大水锤压强出现的频率，从而改善洗井效果。

(5)水锤波透过滤水管上的过滤器会发生衍射和干涉现象，减小封隔段长度L会提高最大干涉压强出现的密度和频率，从而改善洗井效果。

(6)在弹性模量较大的铸铁管、井管直径与壁厚比较小、填砾厚度适中的井中利用水锤效应洗井效果会更好。

(7)在水锤压强推算过程中没有考虑摩擦阻力做功。

(8)实际上，阀门突然关闭时，地下水从含水层透过井壁和管壁向井中流动时会受到阻碍，也会受到压缩产生水锤效应。

［1］ 刘建刚．洗井工艺［M］．湖北武汉:中国地质大学出版社，1990:81－84．

［2］ 王学芳．工业管道中的水锤［M］．北京:科学出版社，1995:1－2．

［3］ 周亨达．工程流体力学［M］．北京:冶金工业出版社，1988:152－155．

［4］ 古丽姗．弹簧振子势能的一种简便分析方法［J］．长春师范学院学报，2010，29(4):57 －61．

［5］ 刘义春．纵波干涉的规律及其应用［J］．物理通报，2000，(9):11－13．

［6］ 杨宝奎 ，等．水锤计算中压力管道的分段问题研究［J］．水利水电技术，2007，(1):53 －55．

［7］ 杨春敏，张景松．水锤及水锤压力波在水系中传播的分析与试验［J］．流体机械，2014，(9):10 －13．

［8］ 梁其东，韩淑婷，张鑫，等．水锤理论模拟分析与防护技术应用研究［J］．城镇供水，2014，(5):89 －92．