曲臂式高空作业平台三铰点位置优化❋
班山岭,高崇仁,殷玉枫
(太原科技大学 机械工程学院,山西 太原 030024)
0 引言
曲臂式变幅机构铰点数目多、伸缩臂受力随变幅角度变化复杂,变幅机构三铰点受力计算和位置布置比传统三铰点变幅机构更加复杂。本文对臂架进行受力分析,在此基础上对其建立优化数学模型,并确定优化目标以及约束条件[1]。
1 力学分析
本文以某型曲臂式高空平台车为例进行分析。该型曲臂式高空作业平台的作业高度为16m,结构简图如图1所示。其基本臂与上臂均为两节伸缩臂,臂架上有两处变幅机构(上变幅机构与下变幅机构),本文以下变幅机构为研究对象,下变幅机构的变幅范围(变幅角度0°~85°)以及伸缩臂的伸缩范围已经确定[2]。

图1 某曲臂式高空作业平台的结构简图
由于下变幅油缸受力大小受上变幅机构变幅角度的影响,因此计算时要把上变幅机构的变幅角度考虑在内,上变幅机构的变幅范围已知(-7°~50°),作业平台始终保持水平,三角板与水平的夹角始终保持恒定。由力学分析可以容易地确定下变幅油缸受力最大工况应该为以下两种工况中的一个:①基本臂水平且完全收缩,上臂在最大变幅角度且完全伸出;②基本臂在最大变幅角度且完全收缩,上臂水平且完全伸出。下面分别计算这两种工况下铰点C处的力矩大小。
(1)工况一下铰点C处的力矩为:

其中:La1,La2为各节基本臂重心到B点的距离;L1为基本臂完全伸出时的长度;Lb1为上臂第一节臂到F点的距离;L2为上臂全伸出时的长度;Q为最大载重;q为飞臂及平台自重;Ga1,Ga2,Gb1,Gb2为各节臂的自重估算值。
(2)工况二下铰点C处的力矩为:
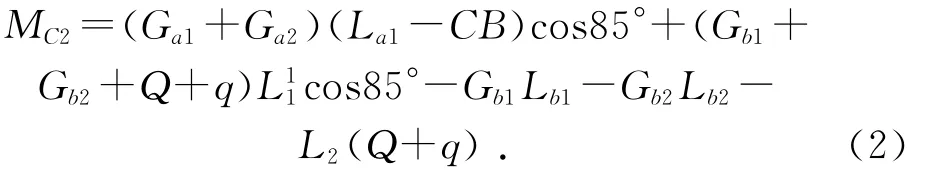
其中:为基本臂全收缩时的长度;Lb2为上臂第二节臂到F点的距离。
将各参数分别代入式(1)、式(2)可计算得出Mc1和Mc2,由计算结果分析可知工况一为危险工况。选择工况一作为优化力学模型,工况一下上臂、小臂及工作平台对基本臂的力矩M为:

2 数学模型的建立
2.1 设计变量的确定
图2为三铰点参数图[3]。其中,Δ为变幅油缸的非工作行程,h为油缸上铰点D到臂架轴线的距离。动臂根铰点C位置固定,油缸上铰点D为根据臂架设计出的固定位置点。所以,三铰点优化的设计变量为油缸下铰点A的两个坐标值X1和X2以及油缸的活塞行程S(设为X3)。把设计变量表示为向量形式为X=(X1,X2,X3)。
2.2 目标函数的建立[4]
2.2.1 变幅油缸受力最小目标函数的确定
综上所述,如果想要在初中语文教学过程中培养并提高学生的语文核心素养,教师就必须要坚决贯彻“生本理念”的同时还要重视教学实践,结合具体的教学情况采用加强学生语言运用能力、培养学生思维能力以及强化高学生审美鉴赏能力的方式来将初中语文教学核心素养提升到一个新的层次,为实现初中语文高效课堂打下基础。
设臂架及工作平台的惯性力忽略不计,由力的平衡原理可知:∑MC=0,则变幅油缸的受力N为:
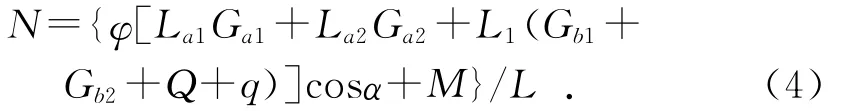
其中:φ为起升冲击系数;L=[CA·CD·sin(α+∠CAB)]/AD。
图2中各几何参数之间的关系为:
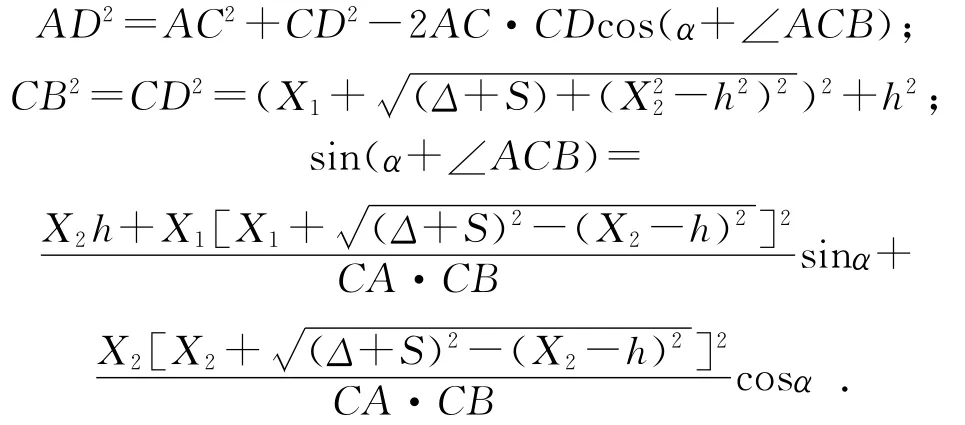
显然,变幅油缸推力N完全可以由给定的设计变量表示,即N=N(X)。则变幅油缸受力最小目标函数为:F1(X)=N(X)。
2.2.2 伸缩臂危险截面处受力最小时目标函数的确定伸缩臂危险截面为铰点D处,根据力矩平衡原理,该处的力矩为:
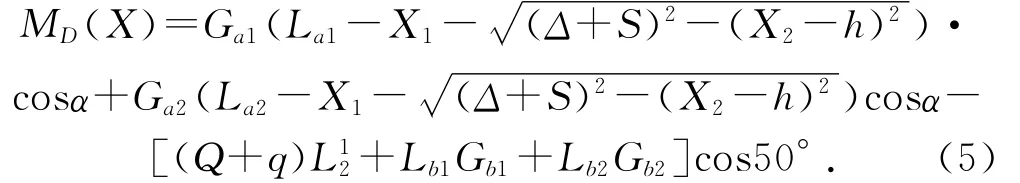
其中:为上臂全缩进时的长度。则变幅油缸受力最小目标函数为:F2(X)=MD(X)。
2.3 约束条件的建立
(1)根据实际问题要求确定的变量范围为:

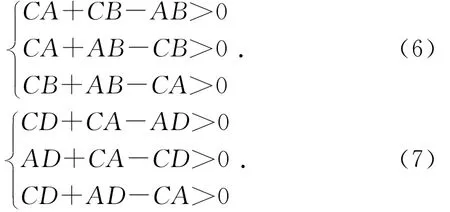
(3)满足最大起升角85°时约束为:
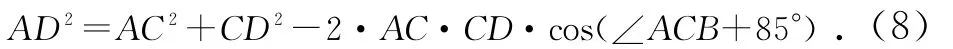
3 MATLAB求解
本文处理的问题属于多目标优化问题,由于约束条件都是非线性的,故选用有约束非线性优化问题fmincon函数[5]。
本文选择最危险工况,即工况一进行分析。在对两个目标进行优化计算时,由于两个目标函数不是一个数量级,故将目标函数简化为:
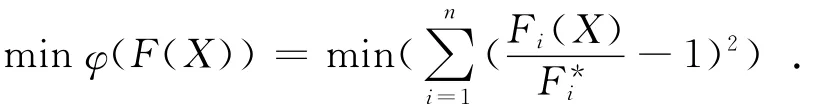
其中:i=1,2。
此目标函数称为虚拟目标函数,其中F*i表示在同样约束下,相同的设计变量范围内单目标函数的最优值。
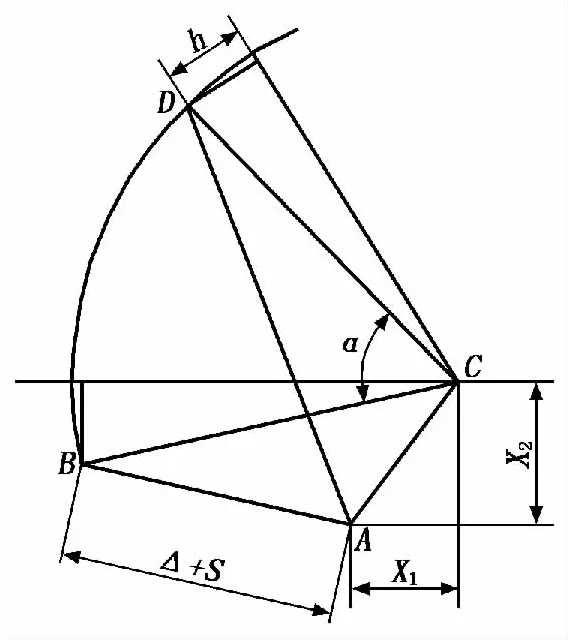
图2 三铰点参数图
4 优化结果与分析
把各设计参数的数值代入到数学模型中,运用MATLAB优化工具箱中的fmincon函数进行优化计算。非线性约束问题的最优解与初始点的选取关系密切,不同的初始点会得到不同的局部最优解。根据以前的设计经验选取初始值为X0=(540,527,1 142)。
图3为3个设计变量最后的优化结果。目标函数经过10次迭代,迭代的终止条件为目标函数值的容差小于设定的容差[6]。优化前与优化后的对比见表1。
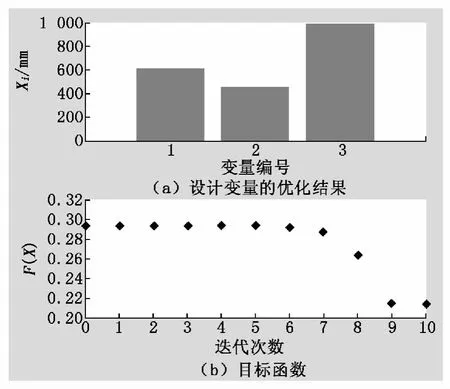
图3 目标函数与迭代次数

表1 优化前与优化后的对比
5 结论
根据多目标优化理论,应用MATLAB优化工具箱中非线性约束多目标优化函数fmincon函数对曲臂式高空作业平台三铰点进行优化,给高空作业平台的铰点设计提供了新的设计思路。
[1] 何清华,朱俊霖,王石林,等.伸缩臂叉装车变幅机构的铰点位置优化[J].华中科技大学学报(自然科学版),2011,39(s2):423-425,429.
[2] 余小兵.用VC++优化计算油缸变幅起重机三铰点位置[J].软件导刊,2012,11(4):90-92.
[3] 王津.自行式高空作业车作业臂有限元分析与优化设计[D].西安:长安大学,2009:23-24.
[4] 王辉.新型混合臂式高空作业车工作臂有限元分析及改进设计[D].南京:东南大学,2008:35-40.
[5] 林亮.高空作业平台伸缩臂有限元分析及变幅铰点优化[D].西安:长安大学,2010:36-37.
[6] 杜向阳,王进,马军星,等.PT25蜘蛛式高空作业平台伸缩臂变幅铰点优化[J].建筑机械,2011(8):91-94.

