考虑紊流效应和温黏关系的滑动轴承故障分析

赵文刚，韩 韬

（青岛经济技术开发区 热电燃气总公司，山东 青岛 266555）

0 引言

轴瓦破裂、碰磨是重载轴承经常发生的故障，不仅损害轴承的几何形状，还影响油膜的压力分布，降低轴承的使用寿命［1］。气轮机用圆柱瓦轴承经常在重载和波动载荷下工作，在此情况下，轴承会处于完全润滑与混合润滑状态之间，易发生碰磨故障［2］。从以往的故障形式来看，轴瓦破裂位置一般在最小油膜厚度的上游，即最大油膜压力处。而本次的破裂位置却明显地出现在下游。为阐明原因，本文在前人研究的基础上，同时计及润滑油的紊流效应和温黏关系，对轴承发生该故障的原因进行了深入研究与探讨。

1 润滑分析的基本理论与公式

1.1 理论计算模型

故障轴承如图1所示。

图1 故障轴承图片

根据故障轴承的相关测试数据与图片，针对轴承的故障类型，建立如图2所示的理论计算模型。

xOby为轴承坐标系，Ob为坐标系原点，Oj为轴颈中心，θ为偏位角，Φ为从y轴负方向开始计量的角度，φ为从偏位线开始计量的角度，ω为轴颈转速，fx为轴承坐标系中沿x轴负方向的油膜力，fy为轴承坐标系中沿y轴负方向的油膜力，ft为切向油膜力，fr为径向油膜力，m为转子质量，g为重力加速度，r为轴颈半径，R为轴承半径。

图2 圆柱轴承数学模型

通常将润滑油膜视为不可压缩流体，忽略油层的重量和运动时的惯性力，紊流工况下轴承中的压力分布可由如下的Reynolds方程［3］描述：

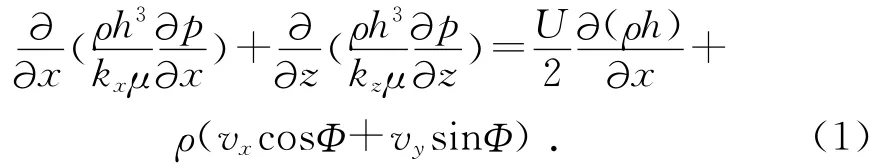
其中：h为油膜厚度，h≈c＋ecosφ，c为轴承间隙，e为轴颈中心相对于轴瓦中心之偏心距；ρ为润滑油密度；μ为润滑油动力黏度；p为油膜压力；vx为x方向上的扰动速度；vy为y方向上的扰动速度；U为两固体表面在x方向上的相对速度；kx，kz为紊流因子，是局部雷诺数的函数。按壁面定律［4］得到其计算公式为：

式（2）中雷诺数可由如下公式计算：

1.2 温黏关系方程

本文采用常用的Reynolds温黏关系式［5］：

其中：Tin为进油温度；μin为在温度Tin下的油液黏度；χ为温黏指数。

1.3 油膜温度场方程

油膜温度场方程为：

其中：T为油膜在任意位置的温度；C为润滑油比热；kf为油膜导热系数；vz为油膜沿z向的扰动速度。

1.4 轴瓦温度场方程

轴瓦的温度场分布可用三维的拉普拉斯方程表示为：

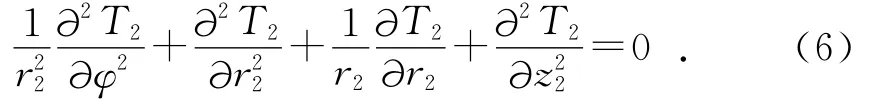
其中：T2，r2分别为轴瓦任意位置处的温度和半径。

1.5 边界条件

1.5.1 油膜温度场边界条件

（1）设进油温度Tin为常数，则进油处沿油膜厚度方向的油温可按下式确定：

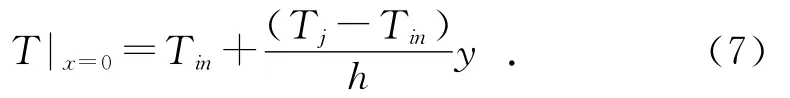
其中：Tj为轴颈表面温度。

（2）轴颈表面温度可采用绝热边界条件，轴颈表面热流量沿周向积分为零，即：

（3）在轴瓦表面，采用热流连续的边界条件，即导热边界条件：

其中：kb为轴瓦导热系数；Rb为轴瓦半径。

（4）考虑温度场分布，还需增加一个轴向的初始条件。对于径向轴承，根据轴向对称性质，当z＝0时有：

1.5.2 轴瓦温度场边界条件

（1）轴瓦入口处，x＝0时：

（2）轴瓦出口处，x＝γ时：

其中：γ为轴瓦半圆周长度。

（3）用Tb2表示环境温度，假定为常数。规定轴瓦与外界接触面r2＝Rb2时：

其中：Rb2为轴承外径。

1.5.3 油膜压力边界条件

对于圆柱轴承，关于压力条件有不同的假设［6］，本文在计算时采用Reynolds边界条件：

其中：p0为环境压力。

2 计算结果与分析

表1为轴承与润滑油的主要参数。

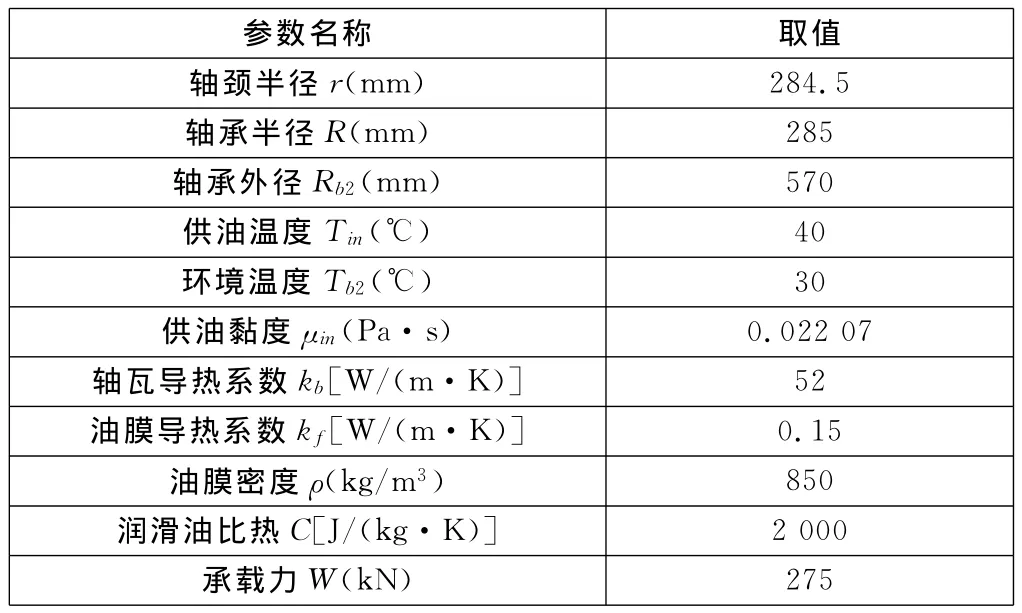
表1 轴承与润滑油主要参数

2.1 油膜压力与厚度

当按层流理论计算时，紊流因子取不变值12；当按紊流理论计算时，紊流因子是随着雷诺数变化的，按式（3）计算雷诺数后，代入式（2）可求得紊流因子。对应层流计算数据，在偏心率ε＝0.7、偏位角θ＝44.2°时，承载力W＝276 145N，接近故障轴承的静态工作点。其压力分布如图3所示，可得额定转速时最大油膜压力pmax＝5.7MPa，出现在周向φ＝292.4°处。

图3 层流理论计算压力分布

根据紊流理论计算结果，故障轴承对应的静态工作点大约在偏心率ε＝0.61、偏位角θ＝53.8°处，此时承载力W＝276 694N。其压力分布如图4所示，额定转速时紊流理论计算的最大压力pmax＝4.96MPa，在φ＝304°处。

两种理论计算的油膜厚度分布如图5所示，层流理论对应的最小油膜厚度在φ＝314.2°处，紊流理论对应的最小油膜厚度在φ＝323.8°处。

由以上计算结果可以看出，考虑紊流效应计算的轴承静态工作点接近实际轴承的运行状况，并且周向最大压力处接近轴瓦破裂位置。

图4 紊流理论计算压力分布

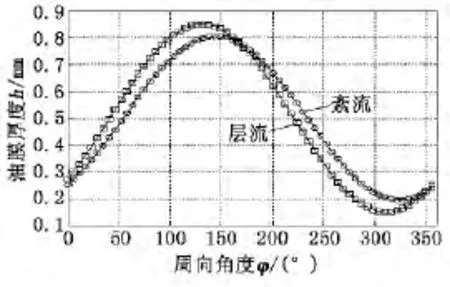
图5 油膜厚度分布曲线

2.2 油膜温度分布

按表1提供的数据，计算了轴承载荷不变的情况下，不同转速时温度沿下轴瓦周向与径向的分布规律，坐标从进油口处开始。图6分别给出了两种转速下不同油膜厚度位置的温度随周向坐标的变化曲线。

由图6可以看出：同一载荷下，随转速升高，油膜温度升高；在相同转速下，不同油膜厚度位置温度随转子转向不断升高，且越接近轴瓦表面温度升高越快。当转速为3 000r/min时，出油口对应轴瓦表面的温度约为56℃左右，与机组现场记录的正常轴承出油温度接近。

3 结论

（1）按紊流理论计算的油膜最大压力、回油温度与机组现场测试的结果基本吻合。考虑紊流效应，在相同偏心率下，油膜承载力比按层流理论计算值偏大，且随着偏心率的增大，两者值相差也越大。

（2）计算的最大油膜压力与轴瓦破裂位置基本接近。随着油温的升高，轴承静态工作点下移，并且最小油膜厚度减小，在最小油膜厚度处与轴颈发生了碰磨，造成了本文所示轴瓦破裂位置发生在碰磨位置的下游。

图6 两种转速下不同油膜厚度时油膜的温度分布

［1］陈立德.机械制造装备设计［M］.北京：高等教育出版社，2008.

［2］杨国安.机械设备故障诊断实用技术［M］.北京：中国石化出版社，2007.

［3］杨沛然.流体润滑数值分析［M］.北京：国防工业出版社，1998.

［4］王小静，张直明，孙美丽.复合型紊流润滑理论模式的研究［J］.摩擦学学报，2000，20（2）：127-130.

［5］邓枚，孙军，符永红，等.计及轴受载变形的粗糙表面轴承热弹性流体动力润滑分析［J］.机械工程学报，2010，46（15）：95-101.

［6］刘大全，苗同臣.滑动轴承广义雷诺方程的一维快速解法［J］.中国电机工程学报，2010，30（29）：85-89.