基于分形理论的高速自动机故障诊断❋
陈玉青,潘宏侠,雷智强,刘会倩
(1.中北大学 机械工程与自动化学院,山西 太原 030051;2.中国人民解放军66336部队92分队,河北 高碑店 074000;3.长城汽车股份有限公司,河北 保定 071000)
0 引言
在故障诊断技术领域,信号的分析与处理是最关键的一步。分形理论是基于一种尺度而研究复杂信息问题的,作为一种现代信号分析方法,在振动领域的研究中,尤其是在机械设备诊断和识别领域得到了应用[1,2]。本文基于分形理论对W85高射机枪自动机故障进行诊断。
1 基于网格维数的故障分析
将分形维数作为机械设备振动信号诊断识别的特征量,对其正常状态和几种非正常状态按照相同的采样间隔Δti(i=1,2,…,n,n为采样周期的个数)进行采样,计算第j种状态的网格维数DjΔti和待检信号x的网格维数。
定义维数距离函数为:
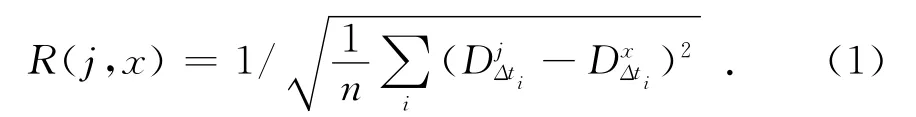
计算待检信号x和第j种状态的维数距离,R(j,x)越大,则两者的相关程度就越强;反之,两种模式就越相离[3]。
2 自动机故障类型分析与实验设置
在机枪自动机的反复设计实验中,机枪的闭锁片曾多次出现裂纹,严重时闭锁块沿裂纹折断,导致机枪停射。本文以W85高射机枪自动机为实验对象,针对现实状况,分别在闭锁片闭锁斜面的圆角处沿其半径方向设置0.5mm深的裂纹槽(故障1)和沿经过闭锁片回转圆心且垂直于闭锁片内平面的方向设置0.5 mm深的裂纹槽(故障2),进行单发射击和三连发射击两种状态的射击,测取正常状态和不同故障状态的加速度振动信号,并将单发和三连发的各一种故障信号作为待测信号。
3 故障实例分析
为了验证分形理论在自动机冲击信号故障诊断方面具有有效性,采集不同工况下的加速度a振动信号进行分析。采样总时间T=5.346 0s,采样周期分别为Δt=77ms,87ms,103ms,123ms和154ms。图1为采样周期为77ms时不同故障状态下原始信号时域图。

图1 采样周期为77ms时不同故障状态下原始信号时域图
根据所采集的数据计算相应的网格维数特征值,见表1。不同采样周期的网格维数如图2所示。

表1 不同采样周期的网格维数特征值
由式(1)可计算出待测信号1,2与各种状态信号之间的维数距离,见表2、表3。
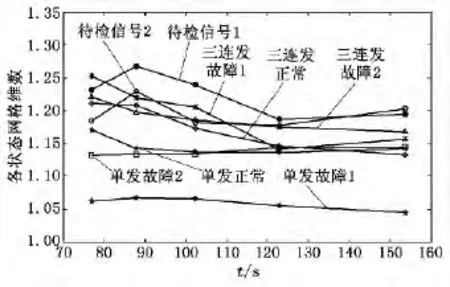
图2 不同采样周期的网格维数图

表2 待测信号1与各状态信号的维数距离
由表2和表3可以看出,待测信号1与三连发故障1的维数距离最大,根据维数距离理论,待测信号1与三连发故障1的相关程度最强。故可判断待测信号1最有可能是三连发故障1,该结果与实际结果一致。同理,待测信号2最有可能是三连发故障2,该结果与实际结果亦一致。

表3 待测信号2与各状态信号的维数距离
4 结论
根据以上结论可知:基于网格维数的分形诊断方法原理简单、容易理解,只要在时域内即可进行故障诊断。
[1]李舜酩,李香莲.振动信号的现代分析技术与应用[M].北京:国防工业出版社,2008.
[2]王宏宇.信号处理的相关理论综合与统一法[M].北京:国防工业出版社,2005.
[3]姚竹亭,潘宏侠,陈越良.分形理论在装甲车辆滚动轴承故障诊断中的应用[J].火炮发射与控制学报,2009(4):66-70.

