GEO光学遥感卫星阳光入侵规避方法

（北京空间飞行器总体设计部，北京 100094）

1 引言

地球静止轨道（GEO）光学遥感卫星是未来光学对地观测卫星技术发展的一个重要领域。由于GEO光学遥感卫星工作轨道距离地球较远，在午夜时分地球阴影无法遮挡卫星（除地影期外），卫星的相机将出现阳光入侵现象，引起如下问题：遮阳罩内壁若长时间接受光照，会引起温度上升，为避免影响卫星的成像任务，对相机温控设计提出了很高要求，通常较难实现；若阳光照射相机内部很深，会对光学反射镜表面的镀膜、焦面探测器等设备造成损伤，严重时将影响相机的使用寿命或使相机失效，导致卫星任务失败。因此，阳光入侵问题是GEO 光学遥感卫星所面临的且必须解决的重要问题。

多个国家和卫星制造公司已经开始GEO 光学遥感卫星的设计和研制工作［1-2］，但在已公布的文献中，均未对阳光入侵问题提供详细的解决方案。欧洲阿斯特里姆（Atrium）公司公布的GEO-Africa卫星每日工作周期示例中显示，在午夜时分卫星通过采用姿态调整180°背地板对日的方式实现阳光入侵规避（以下简称阳光规避）［3］，解决阳光入侵问题，但该方式对卫星平台机动能力、相机热控、太阳翼驱动机构的可靠性、卫星测控能力等方面均提出了很高要求，实现时将付出较大代价，大大增加了卫星的设计难度和研制成本。在这种情况下，通过选取最优的机动路径，利用卫星姿态机动躲避阳光是最佳的方法，因此可将规避方法的设计归结为满足空间几何约束的姿态轨迹规划问题。

目前，卫星姿态运动轨迹规划的研究主要集中于卫星在惯性空间的姿态机动，采用的方法包括势能函数法［4］、半定规划［5］、遗传算法［6］、几何规划［7］等，这些算法各有特点，但主要局限于理论研究，工程应用较少。约束监测算法［8］属于几何规划的一种，最早由NASA 喷气推进实验室（JPL）提出，并已成功应用于“卡西尼”（Cassini）探测器中。此算法主要用于航天器在机动过程中完成天体规避，实现自主姿态规划，但该算法中的姿态轨迹和规避区域均为惯性固定，不适用于阳光规避任务中规避区域相对惯性坐标系不断变化的新特性，同时侧重于研究外界约束对航天器的影响，而忽略了对航天器自身使用约束的考虑。针对上述问题，本文在约束监测算法的基础上进行了适当改进，提出了一种应用约束规避算法的GEO 光学遥感卫星在轨自主阳光规避方法，在综合考虑并明确多项卫星设计工程约束后，将其转换为空间几何约束条件，利用动态约束和静态约束作为规避机动的输入因子，进而实现卫星自主姿态规划，使其适用于卫星阳光规避问题。

2 阳光规避方法

2.1 约束描述

卫星是一个复杂系统，由相关的分系统或独立部件有机地组合成一个整体，因此，在应用约束规避算法解决GEO 光学遥感卫星阳光照射问题时，应充分考虑卫星设计时的约束条件，如GEO 遥感卫星任务需求约束、相机使用约束、电能约束、姿态敏感器使用约束、姿态机动能力约束、热控能力约束及测控能力约束等，在把握各个组成部分之间的相互联系、相互作用和相互协调的前提下，以最小的代价最有效地利用现有技术成果，进行最佳组合，在遵循整体优化的原则下完成设计。

本文在设计阳光规避方法时，首先将卫星设计的工程约束条件转换为空间几何约束条件，如相机使用约束或姿态敏感器使用约束，是要求阳光禁止进入相机或敏感器的视场范围内，否则敏感元件将短暂致盲，甚至损坏。假设阳光入射矢量S在本体坐标系下的投影坐标为Sb＝（sbx，sby，sbz）T，需要规避的相机或敏感器光轴矢量V在本体坐标系的坐标为Vb＝（vbx，vby，vbz）T，定义θ为所设置的相机或敏感器的视场角或约束角，则通常该类约束可表达为

电能约束是指太阳电池阵方向矢量与阳光入射矢量夹角达到一定要求，以满足电能供给；热控能力约束是指为降低设计与研制代价，要求卫星南北板阳光照射情况要满足一定条件，以确保卫星上所有仪器、设备和星体本身构件的温度处于要求范围内；测控能力约束是指卫星测控天线与地面站保持一定夹角，以确保时刻保持与地面的通信。假设由各分系统设计方案所决定的约束矢量U在本体坐标系下的坐标为Ub＝（ubx，uby，ubz）T，定义φ为所设置的约束角，通常该类约束可表达为

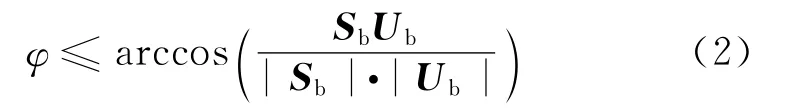
几何约束关系如图1所示。

图1 几何约束关系示意Fig.1 Diagram of geometric constraint relations

由于阳光入射矢量S通常在惯性坐标系下描述，要将其转换到本体坐标系下表示。

式中：SI＝（sIx，sIy，sIz）T为阳光入射矢量在惯性坐标系下的矢量坐标；CBI为卫星的姿态余弦矩阵；q0和q＝［q1q2q3］为姿态四元数；叉乘矩阵［SI×］＝

动力学约束一方面来自执行机构的输出能力，如推力器存在的最大脉冲，动量交换装置存在的最大转速；另一方面来自星上敏感器、相机的运动速度限制，如保持星敏感器的星图跟踪，陀螺采样频率限制［9］。为求得问题并简化计算，通常采用椭球约束形式建模，在形式上最终统一归结为对星体转动角度和角加速度矢量随姿态运动状态的运动学不等式［10］。令ωc＝（ωcx，ωcy，ωcz）T为角速度，ωm＝（ωmx，ωmy，ωmz）T为角速度约束椭球的半长轴，则角速度约束可以表示为

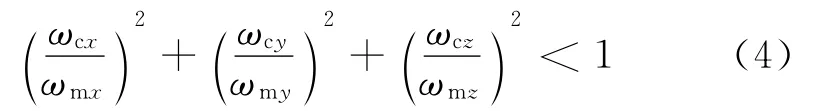
同理，令ac＝（acx，acy，acz）T为角加速度，am＝（amx，amy，amz）为角加速度约束椭球的半长轴，则角加速度约束可以表示为

2.2 方法描述

约束规避算法的核心是空间几何。在充分考虑各方面约束条件后，根据第2.1节所述的θ和φ，最终选取一个最优的θmax设定为规避角，以相机光轴矢量为轴线，θmax为半锥角建立一个躲避锥。卫星首先对阳光入射情况进行实时监测，判断躲避锥与阳光入射矢量的相对位置关系，给出规避信息；当进入阳光规避模式后，根据规避信息及当前卫星姿态，在考虑角速度和角加速度的限制下，应用约束规避算法完成姿态轨迹规划。

2.2.1 约束监测

卫星在机动和成像过程中均要对阳光入射矢量S和相机光轴矢量V之间的约束进行监测。定义单位矢量坐标R为

阳光入射矢量S与相机光轴矢量V的夹角变化率ωr为

式中：Cb＝（cbx，cby，cbz）为阳光入射矢量在本体坐标系中的运动角速度矢量坐标；ωb＝（ωbx，ωby，ωbz）为本体角速度矢量坐标。

定义相机光轴矢量与阳光入射矢量夹角为δ，若相机光轴矢量沿着远离太阳的方向运动，即ωr＜0，则不必进行阳光规避；否则，利用当前姿态和角速度进行外推，若外推Δt时间后δΔt满足式（8），则认为将要发生阳光入侵，须立即停止卫星当前任务，进入阳光规避模式，并准备采用约束规避算法进行姿态机动，完成阳光规避。

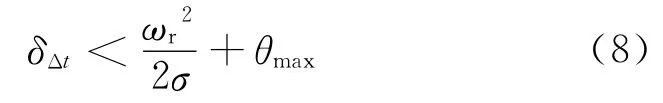
式中：σ为角加速度幅值，ωr2／2σ为考虑卫星运动惯性的预置角。

2.2.2 阳光规避

卫星进入阳光规避模式后，将实时判断相机光轴矢量与躲避锥的相对位置关系，采用最优的路径规划进行姿态机动，即沿着躲避锥切线方向运动。规避锥的切线方向包括沿大弧或小弧运动2 种方向，如图2所示。为了使卫星能够以最短路径到达目标姿态，选用躲避锥与轨道面相对位置关系确定的卫星姿态运动方向，并利用躲避锥中心与卫星指向方向夹角β来表征，即：当β＜0，轨道位于躲避锥的北半圆，为保证光轴指向沿着躲避锥的小弧运动，卫星应向北机动；反之亦然。

图2 环绕方向判断Fig.2 Judgment of surround direction

由于卫星在无机动的情况下维持相对轨道坐标系静止，姿态躲避锥相对轨道坐标系自西向东运动，因此，卫星在俯仰轴方向上可直接利用躲避锥的相对运动完成规避，自身仅进行滚动机动，即当躲避锥运动到恰好与相机光轴矢量相切时，卫星开始进行滚动机动以规避阳光，具体算法如下。

（1）星上轨道计算给出阳光入射矢量在本体坐标系的坐标Sb。

（2）计算阳光入射矢量S与相机光轴矢量V的夹角

（3）当φSV＜θmax时，卫星将进行滚动机动，在考虑留有一定余量的情况下，生成姿态角控制量为θc＝（θcx，0，0），其中θcx由式（9）计算。

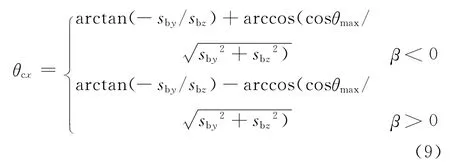
（4）动力学约束检查。根据所生成姿态角控制量，依据动力学约束对其进行校验和修正。首先，校验角速度和角加速度指令ωc＝θc／Δt和ac＝（ωcω0）／Δt是否满足式（4）和式（5）约束，其中，ω0为当前卫星姿态角速度，Δt为采样间隔。如果满足，则以θcom＝θc和ωcom＝ωc-ω0作为姿态控制量；如果不满足，则按照式（10）和（11）对其进行修正，并根据最终角速度和角加速度ω′com和α′com，结合当前姿态和角速度，推知新的姿态控制量ωcom和θcom。

式中：M＝

式中：Mag＝

3 仿真结果与分析

本节对阳光规避方法进行了数值仿真，仿真系统结构如图3所示。采用规避方法后，卫星在春分点和秋分点偏置角度最大，工况最为恶劣，因此本文以春分点为例进行说明。仿真时间为当地时间2015-03-20T22：00-2015-03-21T02：00，仿真步长为1s，卫星轨道参数如表1所示。

图3 仿真系统结构Fig.3 Architecture of simulation system

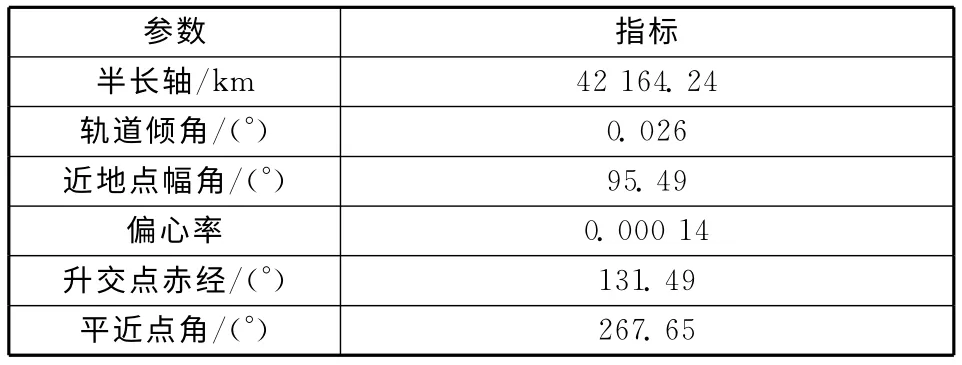
表1 卫星轨道参数Table 1 Parameters for satellite orbit

仿真标称状态为：卫星＋Z轴指向地心，＋X轴指向飞行方向（东），＋Y轴垂直于轨道平面（指向南），卫星太阳翼工作在巡航模式下，卫星在不偏置时太阳翼法线矢量与阳光入射矢量重合。相机光轴矢量与本体坐标系＋Z轴重合，卫星保持三轴稳定姿态，定义躲避锥半锥角θmax为25°。仿真中不考虑地影的影响，动力学仿真采用刚体模型。仿真结果见图4～7。

图4 姿态角曲线Fig.4 Attitude angle curve

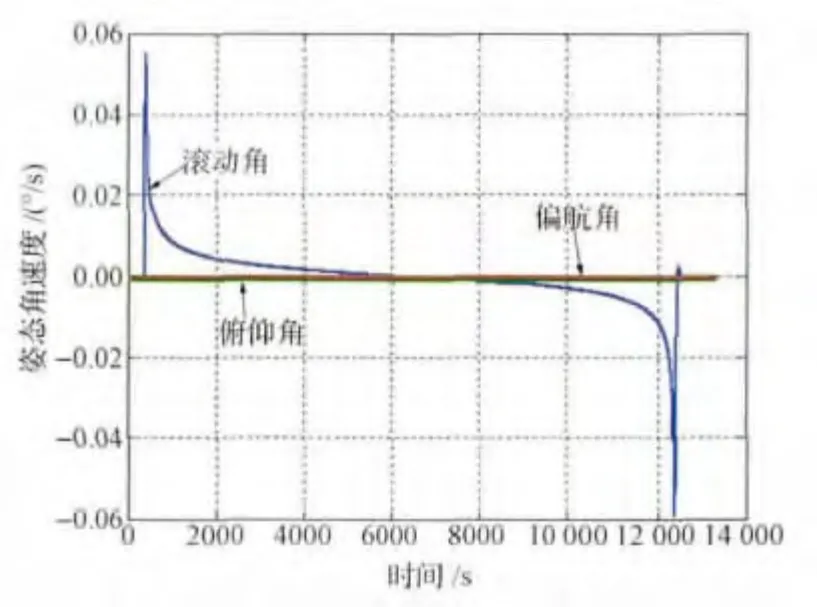
图5 角速度曲线Fig.5 Angular velocity curve

从图4可看到，机动过程中滚动角机动幅度为25°，俯仰和偏航方向基本无偏离，对卫星各分系统产生不利影响相对较小。图5表明，角速度在开始机动时刻和恢复时刻会引起星体角速度波动，滚动角速度变化幅度在0.06（°）／s范围内，满足角速度的约束条件。这一点从图6的2次力矩峰值可以看出：在机动开始时刻，为了使相机光轴快速远离太阳，在滚动方向施加了较大的力矩；在恢复时刻，为了使滚动角快速恢复至标称值，控制力矩也较大。图7显示了仿真期间阳光入射矢量与星体坐标系＋Z轴和轨道坐标系＋Z轴夹角变化过程，从图中可看到，整个机动过程中相机光轴矢量与阳光入射矢量夹角满足25°的约束条件。在整个规避过程中，星敏感器满足使用约束条件；太阳翼法线矢量与阳光入射矢量夹角小于25°，满足电能最小功率输出要求；卫星测控天线波束覆盖区域可包含国土范围内的全部地面站。为了清晰地表现规避过程，将相机光轴与躲避锥均投影在惯性天球上，卫星处于惯性天球中心位置，得到相机光轴投影的运动轨迹如图8所示。

图6 控制力矩曲线Fig.6 Control torque curve

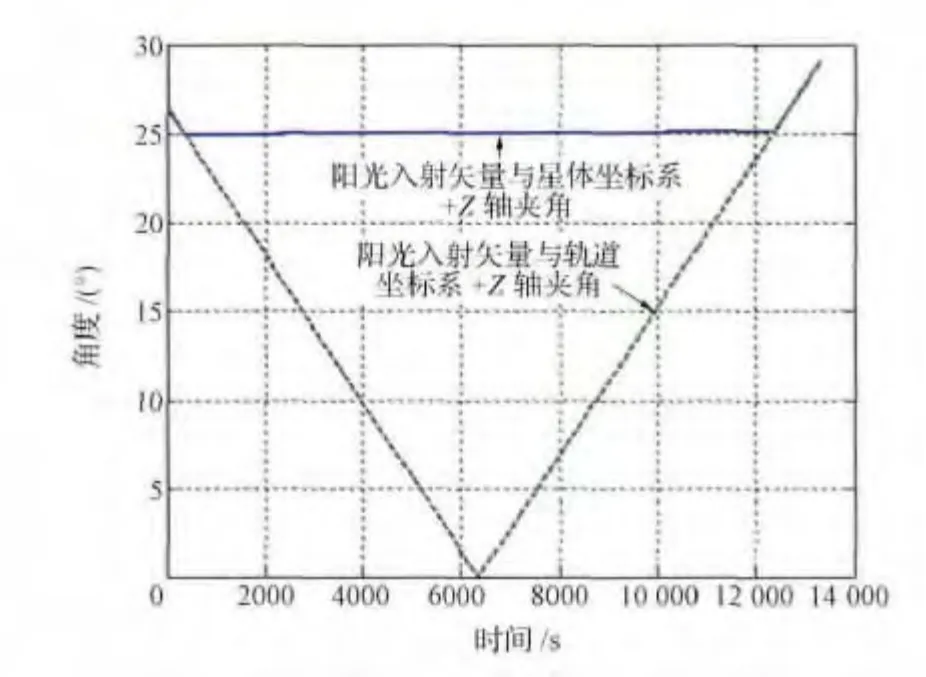
图7 阳光入射矢量与星体坐标系＋Z 轴和轨道坐标系＋Z 轴的夹角Fig.7 Angle between sunlight incidence vector and satellite coordinate＋Zand orbit coordinate＋Z

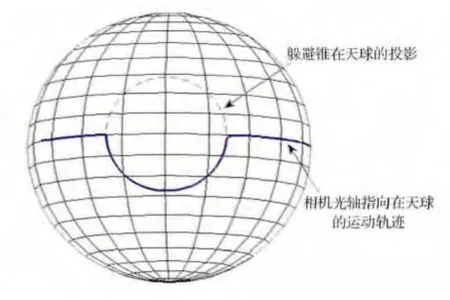
图8 相机光轴在惯性天球的投影Fig.8 Projection of camera axis to inertial celestial sphere

4 结论

本文提出的阳光规避方法，可解决每天午夜时分卫星相机的阳光入侵问题，具有如下优点。

（1）通过调整姿态实现阳光规避，消除了采用相机热门机构方案所带来的经济代价和热门失效的风险；

（2）通过将卫星设计的工程约束条件转换为方法设计的空间几何约束条件，避免了对卫星各分系统设计造成额外的负担，提高了方法的工程应用价值；

（3）方法实现简单，可由控制计算机在轨自主实现，无需地面干预，减少了卫星地面指挥控制系统的负担。

利用阳光规避方法，卫星每日午夜时分均要进行阳光规避，规避时间与阳光入射情况、规避角度以及卫星姿态相关，因此，对夜晚有成像需求的GEO光学遥感卫星如何解决阳光入侵问题，将是后续研究的重点。

（References）

［1］于龙江，刘云鹤.GEO 中高分辨率民用光学对地观测卫星发展研究［J］.航天器工程，2013，22（1）：688-690 Yu Longjiang，Liu Yunhe.Development analysis on GEO civil optical earth observation satellites with midhigh resolution［J］.Spacecraft Engineering，2013，22（1）：688-690（in Chinese）

［2］郭玲华，邓峥，陶家生，等.国外地球同步轨道遥感卫星发展初步研究［J］.航天返回与遥感，2010，31（6）：23-26 Guo Linghua，Deng Zheng，Tao Jiasheng，et al.Preliminary research on development of foreign GEO remote sensing satellites［J］.Spacecraft Recovery ＆Remote Sensing，2010，31（6）：23-26（in Chinese）

［3］Ramos F.GEO-Africa workshop session 1：technical performances［R／OL］.［2013-11-23］.http：／／www.earthobse vations.org／documents／geo＿africa／geo-africafirst-core-team-meeting＿garba＿sambo＿hassan.pdf

［4］Mcinnes C R.Large angle maneuvers with autonomous sun vector avoidance［J］.Journal of Guidance，Control and Dynamics，1994，17（4）：875-877

［5］Kim Y，Meshbahi M.Quadratically constrained attitude control via semidefinite programming［J］.IEEE Transactions on Automatic Control，2004，49（5）：731-735

［6］Kornfeld R P.On-board autonomous attitude maneuver planning for planning for planetary spacecraft using genetic algorithmic［C］／／Proceedings of AIAA Guidance，Navigation，and Control Conference.Washington D.C.：AIAA，2003：207-222

［7］Hablaui H B.Attitude commands avoiding bright objects and maintaining communication with ground stations［J］.Journal of Guidance，Control and Dynamics，1999，22（6）：759-767

［8］Singh G，Macala G，Edward C Wong，et al.A constraint monitor algorithm for the Cassini spacecraft［C］／／Proceedings of AIAA Guidance，Navigation and Control Conference.Washington D.C.：AIAA，1997：272-282

［9］程小军，崔祜涛，徐瑞.几何约束下的航天器姿态机动控制［J］.控制与决策，2012，27（5）：724-730 Cheng Xiaojun，Cui Hutao，Xu Rui.Attitude maneuver control of spacecraft under geometric constraints［J］.Control and Decision，2012，27（5）：724-730（in Chinese）

［10］仲维国，崔平远，崔祜涛.航天器复杂约束姿态机动的自主规划［J］.航空学报，2007，28（5）：1091-1097 Zhong Weiguo，Cui Pingyuan，Cui Hutao.Autonomous attitude maneuver planning for spacecraft under complex constraints［J］.Acta Aeronautica ET Astronautica Sinica，2007，28（5）：1091-1097（in Chinese）