应用激光测高仪提高测绘卫星定位精度的研究

（北京空间飞行器总体设计部，北京 100094）

1 引言

无论在经济建设、国防建设，还是社会发展方面，测绘都具有非常重要的作用。尤其是全局性、战略性的问题，大部分都涉及地理空间信息，由测绘获取的地理空间信息已成为重要的战略资源［1-2］。由于航天摄影测量具有更新快、成本低、不受地区和国界限制的特点，因此世界各国争先研制自己的测绘卫星。定位精度是测绘卫星非常关键的指标，其中的高程精度是建立卫星摄影测量系统的关键内容［3］。目前，国内外的一些测绘卫星，如法国斯波特-5（SPOT-5）测图的相对平面精度为10～15 m，高程精度为10 m［4］；美国艾科诺斯-2（IKONOS-2）卫星的平面定位精度为10～12 m［5］，“世界观测”（WorldView）卫星在有控制点的情况下，定位精度为2～3m［6］；日本“先进陆地观测卫星”（ALOS）可用于绘制1∶2.5万比例尺的地形图，定位精度优于6.1m［7］；我国资源三号卫星在有控制点的情况下，高程精度优于3m，平面精度优于4m［8］。

随着分辨率的提高，测绘相机的质量和体积不断增加，摄影测量模式由多线阵向双线阵发展。双线阵测绘定位精度完全依赖于姿态稳定度和外方位元素值的精度，因此，拥有高精度的卫星星历和姿态测量手段，以及大量的地面控制点，才能获得较高的定位精度。目前，我国卫星平台的定姿精度，很难达到定位精度的要求，提高定位精度的主要方法是通过地面控制点进行修正。然而，国内一些地区由于自然条件、地面特征不明显、交通不便等原因，很难布设控制点，尤其是我国实际控制范围以外或境外地区，所以对于全球测绘，无控制点条件下的卫星遥感影像处理就成为一项必要技术。针对我国目前缺少野外控制点的问题，激光测高仪配合双线阵立体测绘相机是一种有效的解决途径。近年来，星载激光系统成为很多航天强国大力发展的主动遥感手段，激光测高仪能提供地面三维信息，在高程方向上可以达到比较高的精度，如NASA 的地球科学激光测高仪（GLAS）的高程精度可达米级［9］，因此，激光测高仪可作为高程控制点来提高测绘相机的定位精度。用激光测高仪布设控制点，不受交通、地理条件的限制，与人工布设相比成本低，而且控制点分布均匀，获取效率高，能在短时间内获得大量控制点，对于实现无控制点摄影测量具有很大的优势。

目前，我国针对双线阵立体测绘卫星在无控制点情况下提高定位精度的相关理论分析尚不完善，本文从应用激光测高仪提高测绘卫星定位精度入手，首先分析了测绘相机和激光测高仪的误差特性，论证了用激光测高仪提高定位精度的可行性，并借助仿真分析了激光测高仪对提高测绘卫星定位精度的作用。

2 双线阵立体测绘卫星定位精度分析

在无控制点的情况下，双线阵立体测绘卫星的定位是通过前方交会完成的。通过立体像对的左右两影像的内、外方位元素和同名像点的影像坐标测量值来确定物方空间坐标，这个过程叫做前方交会［10］。设（XG，YG，ZG）为地物点物方坐标，（XS1，YS1，ZS1）为前视影像拍照时摄站点S1的坐标，（XS2，YS2，ZS2）为后视影像拍照时摄站点S2的坐标，（XB，YB，ZB）为摄影测量基线在3个方向上的分量，（X1，Y1，Z1）和（X2，Y2，Z2）分别为前视和后视影像点在像空间辅助坐标系下的坐标，（x1，y1）和（x2，y2）分别为前视和后视影像坐标值（对于航天摄影测量，x1＝x2≡0），（x01，y01，f1）和（x02，y02，f2）分别为前视和后视影像的内方位元素，则前方交会的计算公式为

式中：N和N′分别为前视和后视影像点投影到地面上的点投影系数；［X1Y1Z1］T＝R1·［x1-x01y1-y01-f1］T，［X2Y2Z2］T＝R2·［x2-x02y2-y02-f2］T，R1和R2分别为前视和后视影像外方位角元素组成的转换矩阵。

影响双线阵立体测绘卫星定位精度的因素可分为外方位元素和内方位元素，内方位元素对定位精度影响较小，而且其误差可以通过在轨检校消除，因此只考虑外方位元素对定位精度的影响。对式（1）应用泰勒公式展开成线性形式，将各因素看成是独立的，得到地物点物方坐标（XG，YG，ZG）的精度，见式（2）～（4）。其中：（XS1，YS1，ZS1，φ1，ω1，κ1）和（XS2，YS2，ZS2，φ2，ω2，κ2）分别为前视和后视影像的外方位元素；φ1，ω1，κ1和φ2，ω2，κ2分别为前视和后视相机成像时刻的俯仰角、滚动角和偏航角。

为确定外方位元素对3个方向定位精度的影响规律，设定外方位元素中的某个元素误差在一定范围内变化，其他元素误差为0，分别代入到式（2）～（4）中，得到3个方向的定位误差对每个外方位元素的变化率，如图1所示。由于在相同的卫星平台，前视和后视影像的外方位元素测量值的测量精度水平是相同的，相同的外方位元素误差相等，以摄站点坐标XS为例，即ΔXS1≡ΔXS2，所以在式（2）～（4）中，前视和后视影像相对应的外方位元素误差项可以合并，图1中以（XS，YS，ZS，φ，ω，κ）的误差代表前视和后视影像外方位元素误差的综合作用。

图1 单一误差源对定位精度的影响Fig.1 Effect of single error source on positioning accuracy

当卫星参数设置如表1所示时，得到X，Y，Z方向的定位误差分别为18.8 m、18.4 m 和43.6 m。其中，外方位线元素和角元素对定位精度造成的最大误差分别为：摄站点坐标XS的误差对Z方向造成了4.5m 的定位误差，俯仰角φ对Z方向造成了42.9m 的定位误差。

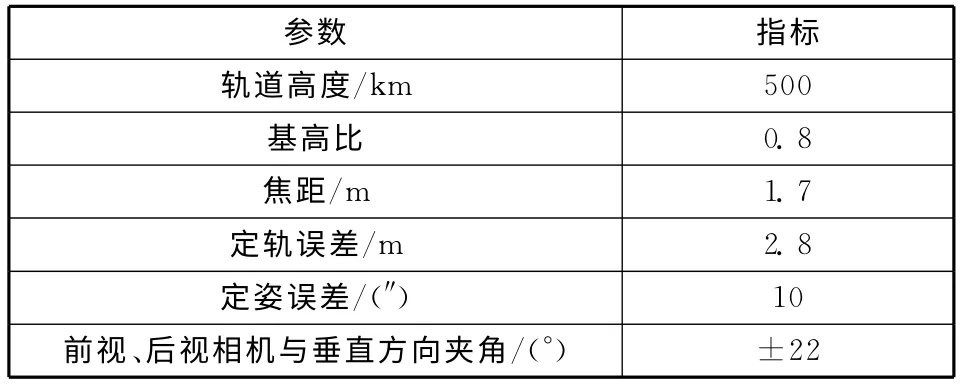
表1 卫星参数设置Table 1 Setting of satellite’s parameters

由以上分析可知，外方位线元素对定位精度的影响较小，测轨数据经过精密事后处理，精度可达到厘米级，基本可以忽略。对定位精度影响最大的是外方位角元素，而在角元素中俯仰角对定位精度的影响最大，1″的俯仰角误差可带来4.3m 的高程误差，因此，俯仰角是影响定位误差，尤其是高程误差的关键因素。双线阵直接前方交会很难达到精度要求，所以引入其他的辅助信息是十分必要的。

3 激光测高仪定位精度分析

激光测高仪测距原理为：由光电探测器件获得光脉冲往返时间，经数据计算得到距离值，见式（5）；结合激光测高仪的位置和姿态信息，经数据处理后可以得到地面目标的三维信息模型。

式中：c为真空中的光速；ΔT为激光往返时间。

当激光测高仪以一定频率发射光脉冲时，即可得到分布均匀的高程控制点。在实际应用中，激光测高仪的配置方式有很多种：可以用单束光垂直入射；可以在测绘相机两侧安装激光测高仪，得到分布于影像两端的高程控制点；还可以三光束“品”字形入射［11］。

激光测高仪激光脚印定位原理如图2所示［12］，Slaser为激光测高仪位置，其坐标为（XSlaser，YSlaser，ZSlaser），P为激光脚印点，其坐标为（XP，YP，ZP），L为 测量的距离值，θ为激光测高仪指向角，（φlaser，ωlaser，κlaser）为激光测高仪外方位角元素。

由图2的几何关系，可以得到激光脚印定位方程为

式中：ai，bi，ci分别为激光测高仪外方位元素中角元素的方向余弦，先绕Y轴转φlaser，然后绕X轴转ωlaser，最后绕Z轴转κlaser，i＝1，2，3。

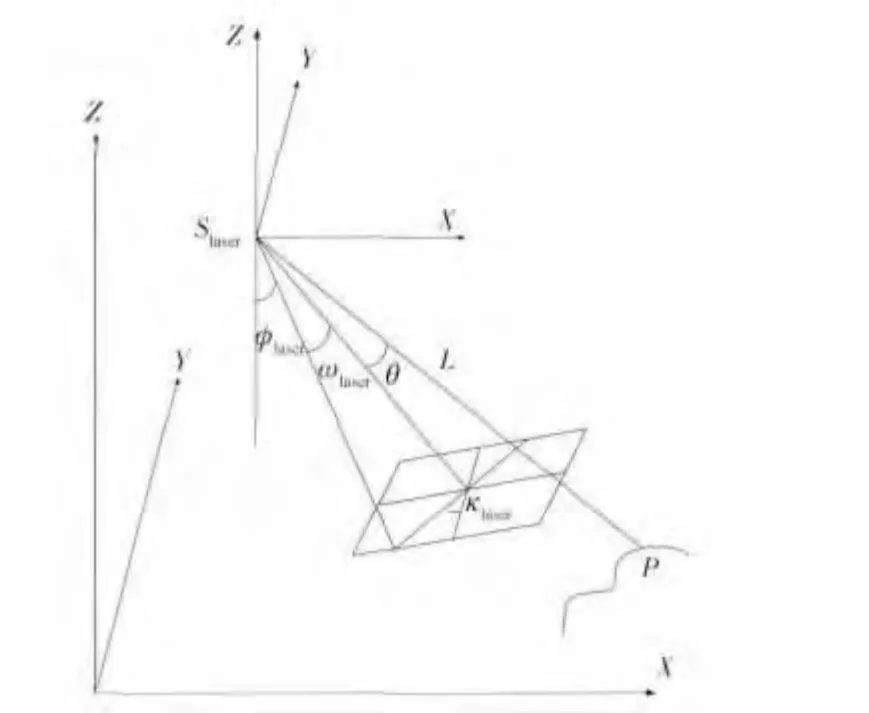
图2 激光测高仪定位原理Fig.2 Positioning principle of laser altimeter

激光脚印的定位精度由以下几方面决定：激光测高仪外方位元素精度（包括线元素和角元素）；激光测距的精度；激光测高仪指向角精度。将式（5）用泰勒公式展开成线性形式，外方位角元素都比较小，近似为0，则物方坐标系坐标轴近似与卫星本体坐标系平行，得到激光足印定位误差模型为

以单束光垂直入射为例，当激光测高仪指向星下点时，即θ＝0，由此可得激光脚印点坐标在X，Y，Z方向的定位误差为

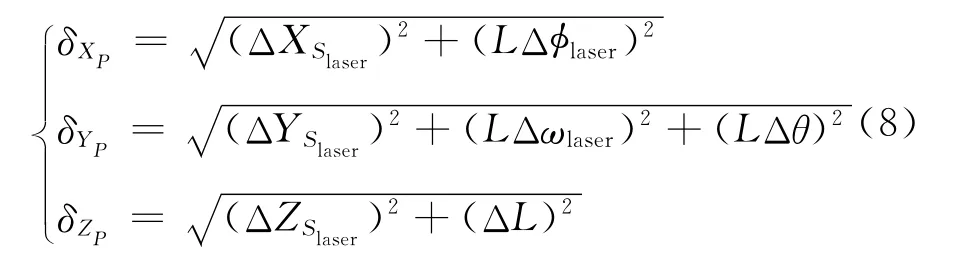
由式（8）可以看出：当激光测高仪近似指向星下点时，高程精度受外方位角元素的影响比较小，这意味着高程精度可以达到很高的要求。下面设定外方位角元素测量误差变化范围为0～20″，研究外方位角元素测量误差对激光脚印定位精度的影响，结果如图3所示。

由图3可知，外方位角元素对激光脚印平面精度影响较大，10″的外方位角元素误差会给X，Y方向带来20多米的定位误差，高程精度受外方位角元素的影响非常小。由此，可得出以下结论：在相同的条件下，通过星载激光测高仪得到的地面点坐标与通过双线阵立体测绘相机得到的地面点坐标相比，高程方向上的精度高得多，但在平面精度方面相差不大。

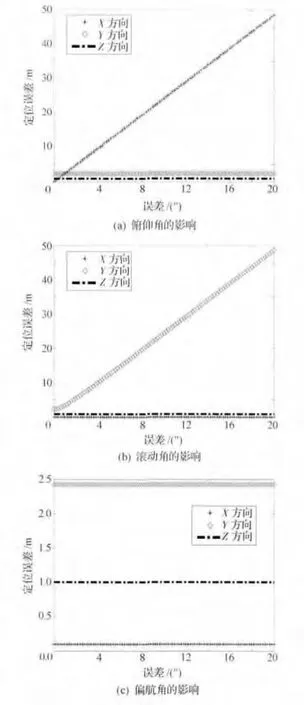
图3 外方位角元素对激光足印定位精度的影响Fig.3 Effect of exterior orientation elements on positioning accuracy of laser point

4 仿真试验

由以上分析可知，采用激光测高数据作为高程控制点是可行的，其原理如图4所示，S1，S2分别为前视、后视相机成像时刻的摄站点位置，Slaser为激光测高仪发射激光脉冲时所处的位置，P为在没有误差情况下通过前方交会得到的激光足印真实位置，dφ1，dφ2，dφ为姿态角的误差，dL是激光测距的误差，P′是存在误差dφ和dL情况下激光足印的位置，P″是存在误差dφ1和dφ2情况下通过前方交会得到的地面点位置，dhlaser和dhI分别是激光足印与通过前方交会得到地面点的高程误差。由于激光足印的高程精度比通过测绘相机得到的地面点的高程精度高得多，因此用P′作为高程控制点来提高双线阵立体测绘相机的定位精度，这需要激光测距系统在测距的同时，还有足印相机可以记录激光足印影像信息。

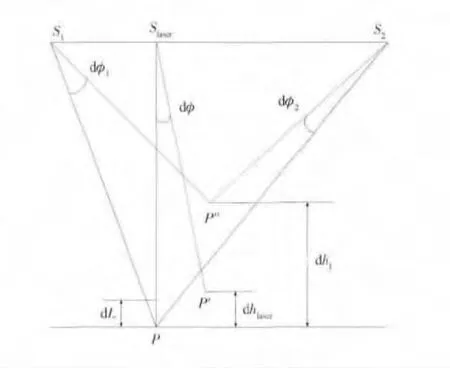
图4 激光测高数据作为高程控制点原理Fig.4 Principle of laser point taken as elevation control point

本文中仿真试验采用的卫星影像数据，包括40个控制点坐标和前视、后视影像的像点坐标，以及两幅影像的有理函数模型（RPC）参数。选取其中一部分控制点作为激光测高仪观测值，一部分为检查点。

将激光测高数据作为高程约束，将激光足印和地物点的像点坐标作为观测值，采用光束法平差，平差方程为

式中：第1个方程是双线阵立体测绘相机影像点坐标误差方程，第2个方程是激光足印影像坐标误差方程；Ai和Bi（i＝1，2）是系数矩阵；V和Vlaser分别为2个方程的改正数；t为所要修正的外方位元素向量；C1和C2分别为待定点和激光足印地面坐标向量。

假设经过精密定轨后，外方位线元素测量精度为0.1m，激光测高仪指向角θ误差为1″，其他误差如表1所示，测量距离值与轨道高度相同，为500km，激光测距精度为1m（包括大气延迟、固体潮、光斑大小带来的误差），将这些数据代入式（8）中，得到激光脚印3 个方向的定位误差为：δXP＝24.240 m，δYP＝24.360m，δZP＝1.005m。

由计算结果可以看出，激光测高仪平面精度较差，下面将激光测高数据只作为高程约束，分析激光测高仪对提高定位精度的作用。仿真数据原始精度如表2所示。

表2 仿真数据原始精度Table 2 Original accuracy of simulation data

经过仿真试验，得到激光测高数据对高程精度的影响情况，结果如图5所示。

图5 试验结果Fig.5 Result of experiment

由图5可以看出，激光测距数据参与平差后，对双线阵立体测绘卫星的高程精度有了明显的提高。

激光测高仪的平面精度受外方位角元素影响比较大，平面误差过大时不宜作为平高控制点直接参与平差计算。取12个控制点，将激光点直接作为控制点参与平差，得到平面误差为34.31m，平面精度依然较差。要提高激光测高仪的平面精度，只通过激光本身可能很难达到明显的效果，因此应该从地面处理入手，如配合少量控制点，或者通过地面检校的方法提高激光足印的平面精度，进而提高双线阵立体测绘卫星的平面定位精度。

5 结束语

本文分析了双线阵立体测绘卫星和激光测高仪的定位误差特性，论证了用激光测高仪提高双线阵立体测绘卫星定位精度的可行性，并且进行了激光测距数据辅助摄影测量的仿真试验。分析结果表明，在相同卫星平台辅助定向参数下，激光测高仪的高程精度要比双线阵立体测绘相机高。激光测高仪的高程精度主要受卫星测轨精度和激光测距精度的影响，受外方位角元素影响较小，与测绘相机相比能达到一个较高的水平，因此激光测高仪能提供大量精度较高的高程观测值。仿真试验结果也表明：增加激光测距数据，测绘相机的高程精度有了显著提高；但是激光测高仪的平面精度与测绘相机相当，很难用激光测高仪提高测绘卫星的平面精度。少量控制点加大量激光测高数据的组合，有助于提高测绘卫星的平面及高程精度，另外，通过地面检校的方法提高激光足印的平面精度，也是一种研究方向。

（References）

［1］宁津生.在统一的总体框架下建设“数字中国”［J］.地理空间信息，2004，2（2）：1-2，6 Ning Jinsheng.The construction of “Digital China”under the unified overall frame［J］.Geospatial Information，2004，2（2）：1-2，6（in Chinese）

［2］孙承志，唐新明，翟亮.我国测绘卫星的发展思路和应用展望［J］.测绘科学，2009，34（2）：5-7 Sun Chengzhi，Tang Xinming，Zhai Liang.Development ideas and application prospects of surveying and mapping satellite in China［J］.Science of Surveying and Mapping，2009，34（2）：5-7（in Chinese）

［3］王任享，李晶，王新义，等.无地面控制点卫星摄影测量高程误差估算［J］.测绘科学，2005，30（3）：9-11 Wang Renxiang，Li Jing，Wang Xinyi，et al.Elevation error estimation of satellite photogrammetry without ground control point［J］.Science of Surveying and Mapping，2005，30（3）：9-11（in Chinese）

［4］刘明川.单线阵CCD 立体影像目标定位误差研究［D］.哈尔滨：哈尔滨工业大学，2011 Liu Mingchuan.Research on error analysis for target location of single-line-array CCD stereo images［D］.Harbin：Harbin Institute of Technology，2011（in Chinese）

［5］Dial G，Bowen H，Gerlach F，et al.IKONOS satellite，imagery，and products［J］.Remote Sensing of Environ-ment，2003，88（1／2）：23-36

［6］高德俊，韩涛，王江涛.WorldView 卫星影像定位能力分析与应用［J］.军事测绘，2011（4）：29-30 Gao Dejun，Han Tao，Wang Jiangtao.Analysis of ability of positioning and application of WordView satellite’s image［J］.Martial Surveying and Mapping，2011（4）：29-30（in Chinese）

［7］Imai H，Katayama H，Sagisaki M，et al.A conceptual design of PRISM-2for Adavanced Land Observing Satellite-3（ALOS-3）［C］／／Proceedings of SPIE Vol.8533，Sensors，Systems，and Next-Generation Satellites XVI.Bellingham：SPIE，2012：1-7

［8］刘斌，孙喜亮.资源三号卫星传感器校正产品定位精度验证与分析［J］.国土资源遥感，2012（4）：36-40 Liu Bin，Sun Xiliang.Accuracy analysis and validation of ZY-3’s sensor corrected products［J］.Remote Sensing For Land ＆ Resources，2012（4）：36-40（in Chinese）

［9］杨秀策，王建荣.星载激光测高系统对地三维定位精度分析［J］.测绘科学与工程，2013，33（2）：53-57 Yang Xiuce，Wang Jianrong.Analysis of three-dimensional positioning accuracy with spaceborne laser altimetry system［J］.Engineering and Science of Surveying and Mapping，2013，33（2）：53-57（in Chinese）

［10］张剑清，潘励，王树根.摄影测量学［M］.武汉：武汉大学出版社，2009 Zhang Jianqing，Pan Li，Wang Shugen.Photogrammetry［M］.Wuhan：Wuhan University Press，2009（in Chinese）

［11］崔云霞，牛燕雄，冯丽爽，等.卫星姿态控制误差及飞行速度对星载激光测高仪测量精度的影响［J］.红外与激光工程，2012，41（4）：913-918 Cui Yunxia，Niu Yanxiong，Feng Lishuang，et al.Effects of satellite attitude control error and flying velocity on satellite laser altimeter measurement precision［J］.Infrared and Laser Engineering，2012，41（4）：913-918（in Chinese）

［12］余俊鹏，孙世君.卫星摄影测量观测技术发展的若干思路［C］／／第二十三届全国空间探测学术交流会论文集.北京：中国空间科学学会，2010：1-6 Yu Junpeng，Sun Shijun.Some strategies about satellite photogrammetry［C］／／Proceedings of the 23rd National Conference on Space Exploration.Beijing：Chinese Society of Space Research，2010：1-6（in Chinese）