DOR测量自适应模型重构算法与实验验证

韩松涛 唐歌实 陈略 曹建峰

（1 航天飞行动力学技术重点实验室，北京 100094）（2 北京航天飞行控制中心，北京 100094）

1 引言

甚长基线干涉测量（Very Long Baseline Interferometry，VLBI）技术能够获取目标高精度的角位置信息［1］，对统一载波测控体制的测距、测速信息形成有效补充［2］。通常深空探测器主动发射具有一定频率间隔的下行侧音信标信号，进行差分单程测距（Differential One-Way Ranging，DOR）测 量［3］。当将两测站的多普勒进行差分时，即可获取目标的差分单程多普勒（Differential One-Way Doppler，DOD）观测量［4］。DOR／DOD 测量模式在“火星快车”（Mars Express［5-6］）、隼鸟号（Hayabusa）、希望号（Nozomi［7-8］）等探测器的导航测轨中得到了成功运用。

DOR 测量的数据处理过程需要参考模型引导相关计算，该引导模型通常依靠轨道预报获取，在目标航天器呈现大时延、快变化的运动特点的情况下，轨道预报精度不可避免恶化，导致DOR 测量处理精度下降。本文提出一种基于侧音信号相频特性的自适应模型重构算法，增强了参考模型精度恶化情况下DOR 处理算法的适应性与稳定性。

2 DOR 测量基本原理

应用于DOR 测量的单频点信号是周期性正弦波，无法像射电信号处理那样通过干涉测量方法对同一波前时延进行判断；通常利用DOR 信号的载波相位信息获得高精度的时延值。

构成基线的两测站接收信号的侧音相位φA-DOR、φB-DOR分别表示为

式中：fDOR为侧音信号频率；r1、r2分别为卫星到两测站的距离；φDOR为初始相位；c为光速。

经相关处理计算干涉相位ΔφDOR为

载波干涉相位与目标到两测站的时延差直接线性相关。依据这一特性，利用卫星下行的两个频率分别为fDOR-1、fDOR-2的侧音信号进行带宽综合处理，实现高精度时延τg的求解。

3 算法原理

处理算法的核心关键是载波相位（差）的求取，尤其是当探测器与测站相对运动变化较大时，此时利用轨道预报信息计算的参考模型精度相对较差，直接应用该参考模型辅助相关处理通常结果较差，甚至无法计算正确结果。

以单测站接收信号为例，对接收信号xA（t）进行建模，信号形式以CCSDS 规范的侧音信号及采集记录格式为标准：

式中：fL-DOR为经过下变频后的侧音信号频率；τA（t）为探测器与测站间的传输时延；t为时间变量。

令N表示理论时延曲线的多项式阶数，则τA（t）表示为

此时时延率可表示为

通过估计接收信号中的多普勒频率fd＿est（t），可以获取时延率的估计值（t）。

则最终时延估计值为

算法处理过程如下：

（1）对接收信号以积分周期为单位进行频率估计，拟合估计结果，并按式（8）、（9）计算初始模型值。

（2）对接收信号进行模型补偿。

（3）更新积分周期，对补偿后的信号同样进行频率估计，拟合估计结果，并计算残余模型值。

（4）更新模型，重复步骤2～4，直至残余积分相位小于先验设定阈值，迭代结束。

（5）对基线两测站采集数据分别进行模型重构，进行差分处理，得到差分时延模型。

（6）利用某一时刻点的轨道参数信息，计算获取差分时延模型中的常数项。

其中先验设定阈值通常以数据的残余模型无相位模糊为准。

4 实验结果

近年来中国深空网建设的步伐逐步加快，为评估深空干涉测量信号处理中心的数据处理分析能力和精度，验证后续与欧洲航天局（ESA）开展干涉测量协同工作的正确性、匹配性，经与ESA 协调，获取了欧洲航天局深空站对“金星快车”轨道器的DOR观测实验数据，实验数据采集时间为2012年8月1日，实验测站包括塞夫雷罗斯和新诺舍深空站，基线长度约11 650km［9］。

本次DOR 实验对X 频段残余载波及高阶谐波信号进行采集记录。图1显示了接收信号频谱特性，其中通道1为主载波，通道2为＋2次谐波，通道3为-14次谐波，通道4为＋20次谐波，采样频率为50kHz。

应用模型重构算法对采集数据进行处理，其中初始模型的计算积分时间为62.5ms，图2显示了每次迭代处理后的残余积分相位，可以看到经过3次迭代后，残余积分相位无模糊现象，算法收敛。

在准确获取引导模型后，进行相关处理计算DOR 及DOD 观测量，其中积分时间为1s，如图3所示。

图1 “金星快车”信号频谱Fig.1 Spectrum of downlink signal of VEX

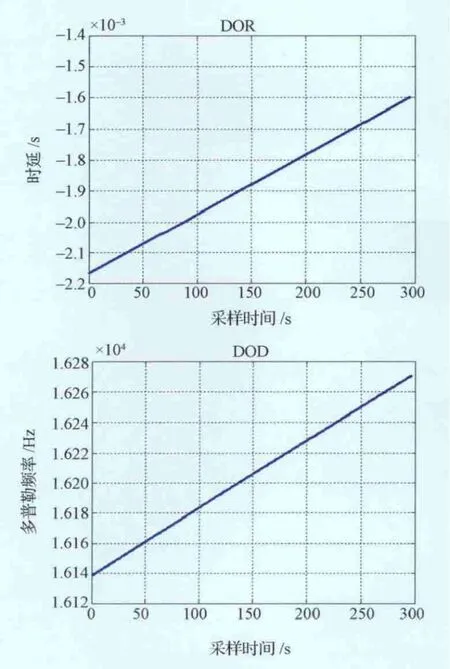
图3 实验结果Fig.3 Experiment results

以ESA 提供的跟踪数据通报（Tracking Data Message，TDM）文件中的观测量作为真值，将干涉相关处理结果进行钟差修正后，拟合插值到同步时刻点，统计测量值与真实值的均方根误差为0.693ns。

依据干涉测量原理，对探测器目标，时延误差与测角精度的关系式近似为

式中：B为基线；θ为基线向量与视向的夹角；δτ为时延精度；δθ为角位置精度。带入基线参数，可得实验观测弧段内的角位置精度在5.2毫角秒量级。

DOD 统计精度为0.005 Hz，依据多普勒频率与相对速度的关系式

式中：f为信号频率；δf为多普勒精度；δv为速度精度。带入侧音信号频率参数，可得实验观测弧段内的速度测量精度在0.2mm／s量级。

5 结束语

本文结合深空探测器大时延、快变化的特点，提出了一种基于侧音相频特性的自适应模型重构算法，极大增强了先验轨道模型精度有限情况下的DOR 处理算法的适应性与稳定性。

对“金星快车”环金星轨道DOR 测量数据的处理结果表明，对应5min观测弧段，采用6阶多项式重构时延参考模型，DOR 结果精度优于ns量级，验证了算法的有效性。本文研究工作为后续我国深空探测工程中的探测器测控具有一定的借鉴意义。

致谢

感谢欧洲航天局地面控制中心（ESOC）测控专家Eric Soerensen和Gerhard Billig提供的数据资源及技术讨论意见。

（References）

［1］朱新颖，李春来，张洪波.深空探测VLBI技术综述及我国的现状和发展［J］.宇航学报.2010，31（8），P1893-1899 Zhu Xinying，Li Chunlai，Zhang Hongbo.Asurvey of VLBI technique for deep space exploration and trend in China current situation and development［J］.Journal of Astronautics，2010，31（8）：1893-1899（in Chinese）

［2］Bagri D S，Majid W A.Estimating accurate relative spacecraft angular position from deep space network very long baseline interferometry phases using X-band telemetry or differential one-way ranging tones，IEEEAC-1557［R］.New York：IEEE，2007

［3］唐歌实.深空测控无线电测量技术［M］.北京：国防工业出版社，2012 Tang Geshi.Radiometric measurement technique for deep space navigation［M］.Beijing：National Defense Industry Press，2012（in Chinese）

［4］吴伟仁，王广利，节德刚，等.基于ΔDOR 信号的高精度VLBI技术［J］.中国科学：信息科学，2013，43（2）：185-196 Wu Weiren，Wang Guangli，Jie Degang，et al.Highaccuracy VLBI technique usingΔDOR signals［J］.Science China：Information，2013，43（2）：185-196 （in Chinese）

［5］Border J S.Innovations in delta differential one-way range：from Viking to Mars Science Laboratory［C］／／21st International Symposium on Space Flight Dynamics.Washington D.C.：2009：1-16

［6］Bagri D S，Majid W A.Accurate spacecraft angular position from DSN VLBI phases using X-band telemetry or DOR tones［C］／／2009IEEE Conference on Aerospace.New York：IEEE，2009：1-7

［7］Kikuchi F，Kono Y，Ping J S.VLBI observation by receiving narrow bandwidth signal from Nozomi［R］.Tokyo：Communications Research Laboratory，2003

［8］Ichikawa R.Hayabusa VLBI observations for development of deep space tracking preliminary report［R］.Tokyo：Communications Research Laboratory，2004

［9］James N，Abello R，Lanucara M.Implementation of an ESA delta-DOR capability［J］.Acta Astronautica，2009，64（11）：1041-1049