北京九龙山不同林分树高与胸径相关生长关系分析

张连金，孙长忠，辛学兵，孔庆云

(中国林业科学研究院 华北林业实验中心，北京 102300)

北京九龙山不同林分树高与胸径相关生长关系分析

张连金，孙长忠，辛学兵，孔庆云

(中国林业科学研究院 华北林业实验中心，北京 102300)

基于幂指数H=aDb对北京九龙山不同林分的树高与胸径相关生长关系进行了分析。结果表明，在12种不同林分中，日本落叶松、栓皮栎、五角枫、糠椴及油松与阔叶树混交林等5种林分的相关生长指数支持弹性相似模型和分形网络模型的预测值2/3，仅有樟子松林及侧柏与五角枫混交林的相关生长指数支持应力相似模型的预测值1/2，无林分数据支持几何相似模型的预测值1，剩余5种林分（侧柏、油松、华北落叶松、白蜡及白蜡与华北落叶松混交林）不支持4种相关模型中的任何一种；一元和多元线性模型分析表明，各种生境因子和林分因子对树高与胸径生长关系的幂指数都没有显著影响。相对于应力相似和几何相似模型，弹性相似模型与分形网络模型更适合描述九龙山林分的树高与胸径相关生长关系。

树高；胸径；相关生长；北京九龙山

森林是陆地上结构最复杂、生物量最大、初级生产力最高的生态系统，在维护全球气候系统、减缓温室气体浓度上升及维持生态安全等方面具有不可替代的作用。个体大小是植物的重要性状之一，对植物的功能属性有着重要影响[1]，不仅决定植物个体的生理生态特征[2]，还影响着生态学各个尺度的格局和过程[3]。

相关生长（allometric scaling）又称异速生长，是描述生物体大小和其它属性之间的非线性数量关系，通常以幂指数（式1）或对数形式（式2）表示[4-5]。

式（1）和式（2）中，Y与X为研究对象的不同生物属性（如个体大小、代谢速率、生物量及元素含量等）；a与b为常数，其中b又称相关生长指数或异速生长指数[6]。相关生长指数b反映了生物体的资源分配策略[7]。自Rubner[8]和Kleiber[9]分别推导出生物的代谢速率与个体质量之间的幂指数为2/3或3/4以来，已有大量的研究表明在生物界中（生理、发育和生活史等方面）广泛存在着以1/3或1/4的倍数为指数的各种相关生长关系[10-19]，还有研究认为相关生长指数不是一个固定的值，而是介于2/3与1之间[20-21]，且有不少学者就相关生长指数b的取值进行了解释[22-29]。

植物相关生长的研究源于生物量分配，目前已广泛地应用于生态学的各个方面[30]，从基因组水平到生态系统水平[31]。其中植物树高与胸径的生长关系是森林生态系统研究和经营中最常用的相关生长关系，对于准备估算森林蓄积、生物量和碳储量具有重要而现实的意义，一直是林学研究的重点。关于树高-胸径（H-D）的相关生长关系研究存在着两种截然不同的观点。传统观点认为，H-D关系随着气候与立地等条件的变化而发生变化[32-35]。而公认的描述树木机械设计的最佳模型[36]：几何相似(Geometry similarity)模型[37-38]、弹性相似模型(Elastic similarity)[37-39]、分形网络(Fractal networks)模型[22-23]和应力相似(Stress similarity)模型[40]则认为，H-D呈不变的幂指数关系，且相关生长指数b分别为1、2/3、2/3和1/2。

本研究以九龙山12个主要林分为对象，研究了不同林分树高与胸径间的相关生长关系，探讨在相同气候条件下不同林分的幂指数的规律及受生境和林分因子的影响，为九龙山不同树种的相关生长研究提供一定的理论依据。

1 材料与方法

1.1 研究区概况

北京市西郊九龙山地区 (39°54′ ～ 39°59′ N，115°59′ ～ 116°07′ E)，属暖温带大陆东岸半湿润季风气候，年均温11.8 ℃，年均降水量623 mm，主要集中在6～9月。年均蒸发量l 870 mm，无霜期216 d。土壤类型属于山地褐土，土层普遍较薄，含石量高。在海拔100～997 m的范围内分布着典型的落叶阔叶林和温性针叶林，主要包括侧柏Platycladus orientalis、油松Pinus tabulaeformis、栓皮栎Quercus variabilis、五角枫Acer mono、白蜡树Fraxinus chinensis、糠椴Tilia mandschurica日本落叶松Larix kaempferi、樟子松Pinus sylvestris和华北落叶松Larix principis-rupprechtii等森林类型。

1.2 研究方法

1.2.1 林分调查

通过踏查，在九龙山选择具有代表性且生长良好、林相整齐的不同林分，设置12块标准样地。对其边界点进行GPS定位，并对标准地内的林分状况进行详细调查，记录样地面积、海拔、坡度、树种组成及年龄等（表1）。对每个样地内胸径1.5 cm以上所有林木编号挂牌，精确测量胸径、树高及冠幅，记录种名、病虫害情况等。

1.2.2 土壤调查

在每块标准地按照“S”型选取5个样点，采用土壤剖面法取0～10 cm，10～20 cm，20～30 cm的土壤样品。将采集的土样带回实验室自然风干、磨碎后过筛，然后装入保鲜袋，用于土壤含水率（风干法）、pH值（电位法）、总有机碳含量（重铬酸钾—外加热法）、全氮含量（半微量开氏法）与速效氮含量（碱解扩散法）的测定。

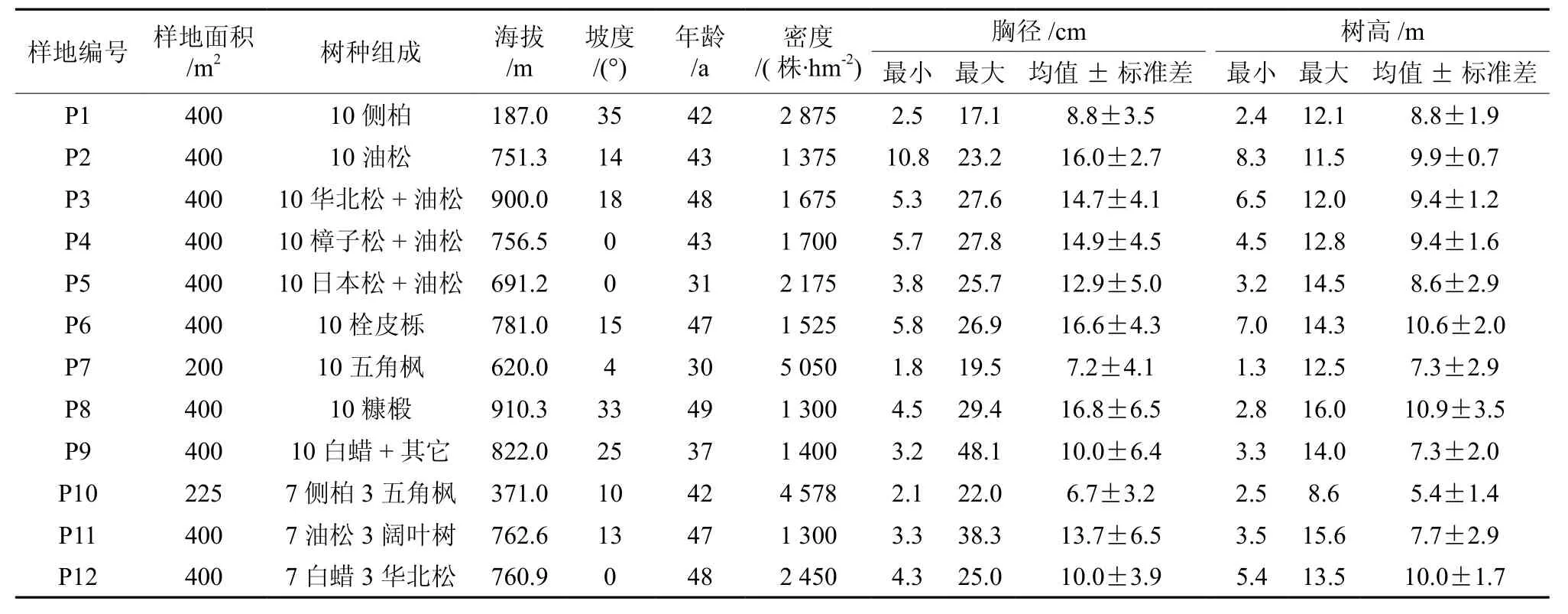
表1 样地基本情况†Table1 Basic characteristics of plots

1.3 数据处理

树高与胸径关系用式（3）表示，采用Forstat 2.0软件中的非线性回归分析进行参数估计[41]。

式（3）中，H为树高；D为树高；a、b为参数。

为研究各种因素对树高与胸径相关关系的影响，采用一元与多元线性回归对相关关系指数b与地形因子、土壤养分指标及林分因子的关系进行分析。在多元线性回归中，采用逐步回归法进行变量筛选。

2 结果与分析

2.1 树高-胸径的相关生长指数

12种不同林分的树高-胸径相关模型拟合结果见表2。从表2可知，所有林分的R2值都大于0.71，且相关生长指数b在0.35～0.73之间。在12个样地中，有5种林分（日本落叶松、栓皮栎、五角枫、糠椴及油松与杨、榆等阔叶树混交林）的相关生长指数b的95%置信区间包含2/3，即在0.05显著水平上与弹性相似和分形网络模型的预测没有显著差异。仅有2个林分（樟子松林及侧柏与五角枫混交林）的95%置信区间包含1/2，支持应力相似模型的预测，而几何相似模型的预测值1则没有任何林分的数据支持。还有5种林分（侧柏、油松、华北落叶松、白蜡及白蜡与华北落叶松混交林）的相关生长指数b的95%置信区间在0.30～0.50之间，不支持4种相关模型中的任何一种。

2.2 生境与林分因子对树高-胸径相关关系的影响

从表3可知，生境因子（海拔、坡度、土壤pH值、含水率、有机质、全氮及速效氮）和林分因子（年龄与密度）对树高与胸径相关生长指数b值的解释力很小，R2小于0.10，且p值远大于0.05，说明单个生境与林分因子本身对树高与胸径的相关生长没有明显的影响。

基于逐步回归法的多元线性回归分析表明，包含坡度、密度、有机质和全氮四个变量因子的线性模型总体的解释力较小，R2=0.33，且p=0.523远远大于0.05（表4）；就各个变量自身的解释力来看，p在0.131～0.576之间（表5），也远远大于0.05。这进一步说明无论是各单个因子、还是不同的生境与林分因子的组合对树高与胸径的相关生长指数都没有显著影响。

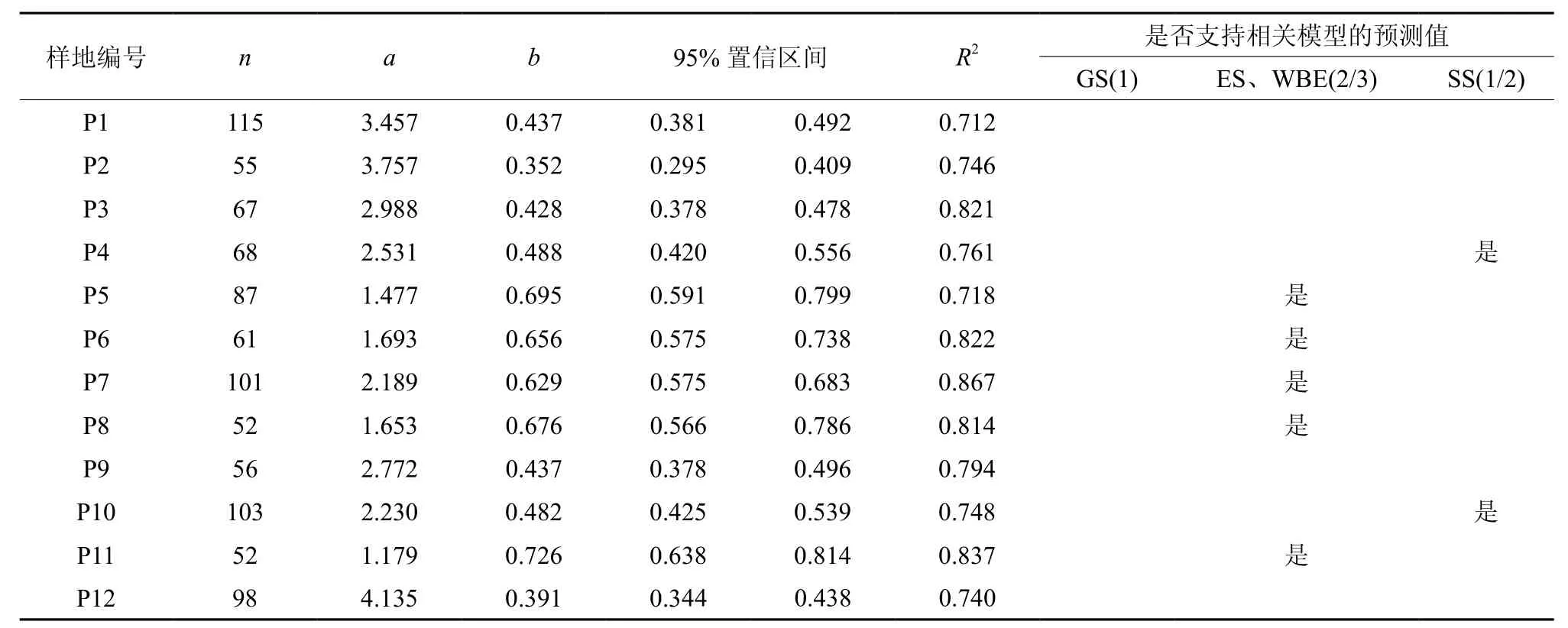
表2 各样地树高与胸径相关关系模型拟合结果†Table2 Fitting results of H-D relationship model in plots

表3 各样地的生境与林分因子对树高-胸径相关生长指数b的解释力Table3 Effects of habitat and stand factors on allometric scaling index(b) of H-D relationship in plots

3 结论与讨论

相关生长关系是基本物理和几何规律对生物体结构要求及进化对生物个体生理效率最优要求的反映，体现了有限的环境资源和生物体内传输能力对生物生长的限制，在理论研究和生产实践中均有重要意义[42]。不仅能为实现生态属性从个体到种群、群落、生态系统的尺度转换提供手段[19]，还可以解决研究中出现的无法直接测量或表征的不同属性的问题，同时还能用以从某些容易测量的指标估算较难测量的生物参数。

本研究的12种林分种，有5种林分（日本落叶松、栓皮栎、五角枫、糠椴及油松与阔叶树混交）的树高—胸径相关关系指数b支持弹性相似与分形网络模型的预测值2/3，仅有樟子松林及侧柏与五角枫混交林2种林分的相关生长指数支持应力相似模型的预测值1/2，无林分数据支持几何相似模型的预测值1，剩余5种林分（侧柏、油松、华北落叶松、白蜡及白蜡与华北落叶松混交林）不支持4种相关模型中的任何一种。这一研究结果与以往林木相关生长的一些研究一致。徐海[43]对吉林蛟河五角枫的树高与胸径相关关系指数b值为0.608 0，支持弹性相似与分形网络模型的预测值2/3；刘敏等[44]关于樟子松的树高与胸径相关关系支持应力相似模型；戴继先[45]对4种不同地位指数的华北落叶松的树高与胸径相关关系进行研究，结果表明仅在地位指数为11时支持应力相似模型的预测值1/2，其它三个地位指数级都不支持4种相关模型中的任何一种。Obrien等[39]的研究表明，大多树种的树高—胸径相关生长关系都支持弹性相似模型，而不支持应力相似和几何相似模型。还有一些研究表明，弹性相似模型更适合描述树木（包括阔叶树）的相关生长关系，而动物和小型植物则更符合几何相似模型[5,46]，这可能与树木的形成机制有关，因为它首先要能够支持自身的重量[46]。

本研究无任何林分数据支持几何相似模型的预测值1，可能与林分的年龄有关，所有林分的年龄都大于等于30 a，明显不是个体发育的早期。因为有研究表明：大部分符合几何相似模型的植物主要发生在个体发育的早期，而弹性或应力相似模型主要发生在植物的成熟阶段。

本研究结果还表明，各种环境、土壤和林分因子对不同林分的树高与胸径的相关关系指数均无显著影响，只能说明该相关生长关系在较小的空间尺度上，受小环境和生物因素的影响较小。因为有研究表明树高与胸径的相关关系在较大环境梯度时，随气候与立地条件的不同而变化[47]。

总之，本研究说明了不同植物的树高与胸径相关关系指数具有较大差异，但是大多支持弹性相似与分形网络模型的预测值2/3。在较小的空间尺度上，树高和胸径相关关系指数受树种自身的基本力学因素制约作用较大，而受环境与生物因素影响较小。

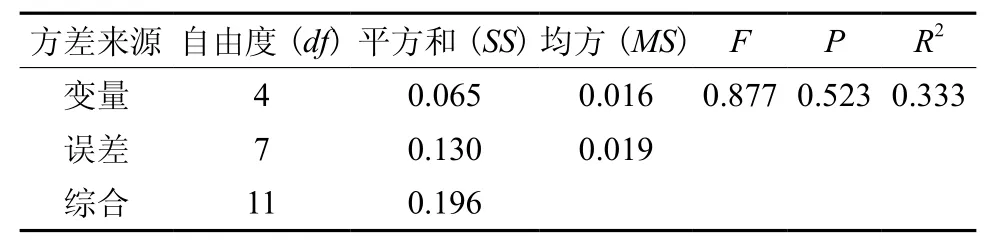
表4 各样地生境与林分因子对树高-胸径相关生长指数b影响的方差分析Table4 Variance analysis for effects of habitat and stand factors on allometric scaling index(b) of H-D relationship of plots

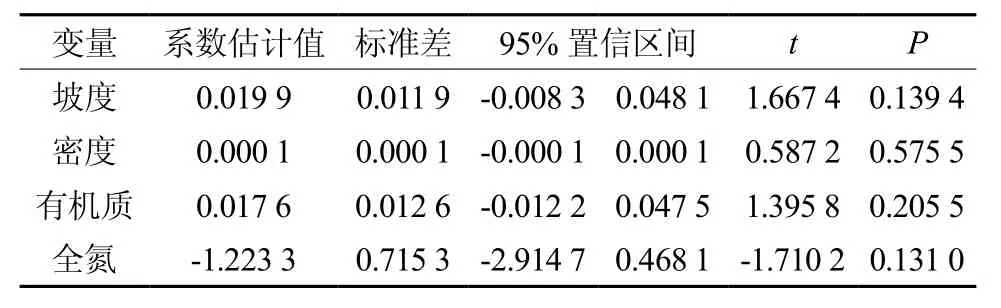
表5 各样地生境与林分因子对树高-胸径相关生长指数b影响的回归系数Table5 Regression coefficients for effects of habitat and stand factors on allometric scaling index(b) of H-D relationship of plots

[1] Makarieva A M, Gorshkov V G, Li B L, et al. Mean massspecif i c metabolic rates are strikingly similar across life`s major domains: evidence for life`s metabolic optimum[J]. Proceedings of the National Academy of Sciences,2008,105(44):16994-16999.

[2] West G B, Niklas K J. Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals[J].Proceedings of the National Academy of Sciences of the United States of America, 2002, 99: 2473-2478.

[3] Brown J H, Gillooly J F, Allen A P, et a1. Toward a metabolic theory of ecology[J]. Ecology, 2004, 85: 1771-1789.

[4] Peters R H. The ecological implications of body size[M].Cambridge University Press, Cambridge, 1983.

[5] Niklas K J. Plant Allometry: the Scaling of Form and Process[M].University of Chicago Press, Chicago, 1994a.

[6] 韩文轩,方精云.幂指数异速生长机制模型综述[J].植物生态学报,2008,32(4):951-960．

[7] Huxley J S. Problems of relative growth[M]. Methuen, London,1932.

[8] Rubner M. On the influence of body size on metabolism and energy exchange (in German)[J]. Zeitschrift für Biologie, 1883,19: 535-562.

[9] Kleiber M. Body size and metabolism[J]. Hilgardia, 1932, 6:315-353.

[10] Economos A C. Gravity, metabolic rate, and body size of mammals[J]. The Physiologist, 1979, 22: S71-S72．

[11] 刘雯雯,项文化,田大伦,等. 区域尺度杉木生物量通用相对生长方程整合分析[J].中南林业科技大学学报,2010,30(4):7-14.

[12] 曾伟生,肖前辉,胡 觉,等. 中国南方马尾松立木生物量模型研建[J]. 中国林业科技大学学报,2010,30(5):50-56.

[13] Heusner A. A size and power in mammals[J]. Journal of Experimental Biology, 1991, 160: 25-54．

[14] Niklas K J. Size-dependent variations in plant growth rates and the 3/4-power rule[J]. American Journal of Botany, 1994b, 81:134-144．

[15 Enquist B J, West G B, Charnov E L, et al. Allometric scaling of production and life-history variation in vascular plants[J]. Nature,1999, 401: 907-911.

[16] Prothero J. Scaling of tree height and trunk diameter as a function of ring number[J]. Trees: Structure and Function, 1999,14:43-48.

[17] Dodds P S, Rothman D H, Weitz J S. Re-examination of the“3/4-1aw”of metabolism[J]. Journal of Theoreticaf Biology,2001, 209: 9-27.

[18] Enquist B J, Niklas K J. Invariant scaling relations across treedominated communities[J]. Nature, 2001, 410: 655-660.

[19] 韩文轩,方精云.相关生长关系与生态学研究中的尺度转换[J].北京大学学报(自然科学版),2003,39(4):583-593.

[20] Makaf i eva A M, Gorshkov V G, Li B L. Biochemical universality of living matter and its metabolic implication[J]. Functional Ecology, 2005, 19: 547-557.

[21] Glazier D S. A unifying explanation for diverse metabolic scaling in animals and plants[J]. Biological Reviews, 2010, 85: 111-138.

[22] West G B, Brown J H, Enquist B J. A general model for the origin of allometric scaling laws in biology[J]. Science, 1997,276: 122-126.

[23] West G B, Brown J H, Enquist B J. A general model for structure and allometry of plant vascular systems[J]. Nature, 1999a, 400:664-667.

[24] West G B, Brown J H, Enquist B J. The fourth dimension of life:Fractal geometry and allometric scaling of organisms[J].Science, 1999b, 284: 1677-1679.

[25] West G B, Brown J H, Enquist B J. A general model for ontogenetic growth[J]. Nature, 2001, 413: 628-631.

[26] Banavar J R, Maritan A, Rinaldo A. Size and form in efficient transportation network[J]. Nature, 1999, 399: 130-132.

[27] Darveau C A, Suarez R K, Andrews R D, et a1. Allometric cascade as a uniting principle of body mass effects on metabolism[J]. Nature, 2002, 417: 166-170.

[28] Reich P B, Tjoelker M G, Machado J L, et al. Universal scaling of respiratory metabolism,size and nitrogen in plants[J]. Nature,2006, 439: 457-461.

[29] Enquist B J, Allen A P, Brown J H, et al. Biological scaling:Does the exception prove the rule?[J]. Nature, 2007, 445: E9-E10.

[30] 贺纪正,曹 鹏,郑袁明. 代谢异速生长理论及其在微生物生态学领域的应用[J]. 生态学报,2013,33(9):2645-2655.

[31] West G B, Brown J H. The origin of allometric scaling laws in biology from genomes to ecosystems: towards a quantitative unifying theory of biological structure and organization[J].Journal of Experimental Biology, 2005, 208: 1575-1592.

[32] Peng C, L Zhang, J Liu. Developing and validating nonlinear height-diameter models for major tree species of Ontarios boreal forests[J]. Northern Journal of Applied Forestry, 2001, 18: 87-94.

[33] Lopez-Serrano F R, A Garcia-Morote, M Andres-Abellan, et al.2005. Site and weather effects in allometries: A simple approach to climate change effect on pines[J]. Forest Ecology and Management, 2005, 215: 251-270.

[34] Feldpausch T R, L Banin, O L Phillips, et al. Height-diameter allometry of tropical forest trees[J]. Biogeosciences, 2011,8:1081-1106.

[35] Banin L, T R Feldpausch, O L Phillips, et al. What controls tropical forest architecture? Testing environmental, structural and fl oristic drivers[J]. Global Ecology and Biogeography, 2012, 21:1179-1190.

[36] Niklas K J. Size-dependent allometry of tree height, diameter and trunk-taper[J]. Annals of Botany, 1995, 75: 217-227.

[37] McMahon T A. Size and Shape in Biology[J]. Science, 1973,179: 1201-1204.

[38] Rich P M, Helenurm K, Kearns D, et a1. Height and stem diameter relationships for dicotyledonous trees and arborescent palms of Costa Rican tropical wet forest[J]. Bulletin of the Torrey Botanical Club, 1986, 113(3): 241-246.

[39] Obrien S T, S P Hubbell, P Spiro, et al. Diameter, height, crown,and age relationships in 8 Neotropical tree species[J]. Ecology,1995, 76: 1926-1939.

[40] Mcmahon T A, Kronauer R E. Trees tructures:Deducing the principle of mechanical design[J]. Journal of Theoretical Biology,1976, 59: 443-466.

[41] 唐守正,郎奎建,李海奎. 统计与生物数学模型计算(Forstat教程)[M]. 北京:科学出版社,2009.

[42] 罗 红,李百炼.异速生长模型研究概述[J].生态学杂志,2011, 30(9):2060-2065.

[43] 徐 海. 天然红松阔叶林经营可视化研究[D].北京:中国林业科学研究院,2007.

[44] 王义霞, 董海凤. 胡椒施肥技术研究进展及我国胡椒施肥现状与对策[J]. 生物灾害科学, 2012, 35(4): 443-446

[45] 井大炜,邢尚军,马丙尧, 等.土壤与植物中钙营养研究进展[J]. 生物灾害科学, 2012, 35(4): 447-451.

[46] Norberg R A. Theory of growth geometry of plants and selfthinning of plant populations: geometric similarity, elastic aimilarity, and different growth modes of plants.[J] American Naturalist, 1988, 131: 220-256.

[47] Wang X P, J Y Fang, Z Y Tang, et al. Climatic control of primary forest structure and DBH-height allometry in Northeast China[J].Forest Ecology and Management, 2006, 234: 264-274.

Allometric relationship between height and diameter at breast height of different stand in Beijing Jiulong mountain

ZHANG Lian-jin, SUN Chang-zhong, XIN Xue-bing, KONG Qing-yun
(Forestry Experiment Center of North China, CAF, Beijing 102300, China)

Based on the power function H=aDb, the allometric relationship between tree height(H) diameter at breast height(D) of different stand in Beijing Jiulong mountain was studied. The results show that, in 5 out of 12 plots (including Larix kaempferi, Quercus variabilis, Acer mono and Tilia mandschurica forest, Pinus tabulaeformis and broadleaf mixed forest), the allometric scaling index between H and D supported the predicted value (2/3) of elastic similarity(ES) and fractal network model(WBE), while only 2 plots(eg. Pinus sylvestris forest, Platycladus orientalis and Acer mono mixed forest) supported the stress similarity model (SS) and no data supported the geometry similarity model (GS). Other 5 plots (including Fraxinus chinensis, Larix principis-rupprechtii, Platycladus orientalis and Pinus tabulaeformis forest, Fraxinus chinensis and Larix principis-rupprechtii mixed forest) not supported any of four relevant models. Both univariate and multivariate linear regression analysis show that both habitat and stand factors did not have signi fi cant in fl uence on the allometric scaling index. It can be concluded that comparing with SS and GS, the ES and WBE are more suitable for describing the allometric relationship between H and D of different stand in Beijing Jiulong mountain.

tree height; diameter at breast height; allometric relationship; Jiulong mountain in Beijing

S758

A

1673-923X(2014)12-0066-05

2014-06-13

中国林科院基本科研业务费专项资金项目（CAFYBB2012004）

张连金（1980-），女，福建三明人，博士，工程师，主要研究方向：森林经营模拟；E-mail：zlianjin1102@126.com

孙长忠（1957-），男，陕西杨陵人，研究员，主要研究方向：森林培育、森林生态；E-mail：sun61@163.com

[本文编校：文凤鸣]