基于运动学的换道安全间距研究
刘艳玲,熊 辉
0 引言
车辆在道路上行驶发生最为普遍的行为一是跟驰,二是换道。换道是一个高度智能化的过程,涉及到横向和纵向的控制,虽然换道行为是一个比较复杂的过程,但国内外对换道模型的研究已经比较成熟。Gipps 模型最早建立换道决策的结构框架,具有开创性意义,为以后选择换道模型奠定了基础;Hidas 等人在Gipps 的基础上进行改进,提出SITRAS 模型,对换道可行性判断提出两个条件。将人车单元当作一个多智能体,考虑了后间距不足时,车辆的竞争合作关系及其减速让行行为,能很好地反映受事故影响的交通状况下的换道行为。之后,又有研究人员提出MITSLM模型,该模型给出了较为详细的自由换道规则,并加入了随机误差项。CORSIM 模型由FHWA(美国联邦公路局)研发,包括FRESIM 模型和NETSIM 模型,这两种模型在美国已经得到一定的应用,FRESIM 模型由动机、利益和紧急三个因素组成;NETSIM 模型中自由换道模型主要由换道动机和间隙检测两部分组成,并在车头间距小至不可忍受或实际运行速度小于给定忍受值1/2 的情况下,驾驶员将考虑换道。
对于换道模型,国内外研究已经相当成熟,以上列举了换道模型中较为经典的模型,这些模型都给以后的研究提供相当深厚的理论基础。
1 驾驶员换道行为分析
驾驶员在行驶过程进行换道选择主要基于:超越慢车、变换到排队长度短的车道及随机变换车道等等。一般情况下,通过对驾驶员换道行为的分析,可以将换道行为的判断过程分为四个阶段(见图1)。
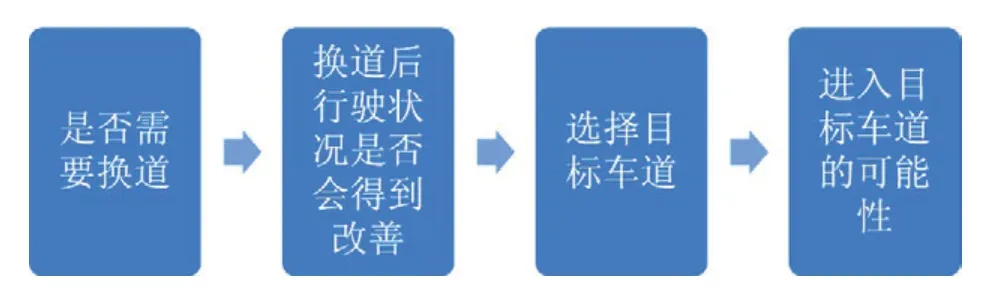
图1 换道判断过程
换道行为是驾驶员为满足自己驾驶的舒适性、驾驶意图而采取的避开本车道换入临近车道的驾驶行为。车辆是否进行车道变换取决于驾驶环境、驾驶目的地及驾驶员本身的特征。当交通流密度处于自由交通流密度及拥堵交通流密度时,车辆存在可换道的间距,因此需要快速行驶的车辆可以通过变换车道来摆脱慢速度行车的限制,从而使驾驶员的驾驶满意度得到提升。
一般情况下,驾驶员在行驶过程中的车道变换可以分为两类,即强制性换道和选择性换道。强制性换道有明确的目标车道,只要目标车道出现合适的间隙,就立即执行换道。目标车道及换道动机都不受驾驶员类型的影响。选择性换道,首先要选择是否需要换道以及需要换道后选择哪一车道作为目标车道;其次观察目标车道及当前车道前后车的运行情况,估计目标车道可接受间隙的大小是否满足换道的需求,若满足则换道,反之则继续在原车道行驶(见图2)。
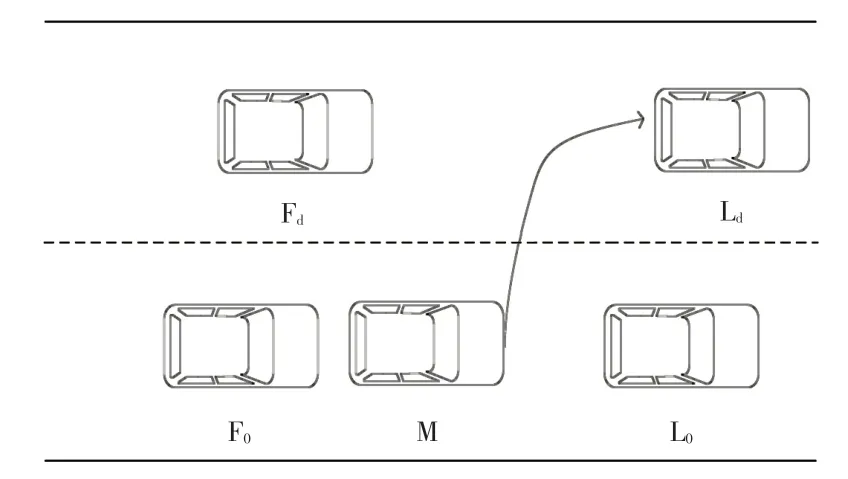
图2 M车与原车道及目标车道车辆的位置关系
2 基于运动学的换道安全间距模型
在建立模型之前强调,因为讨论换道模型,换道是已有的意图,即模型主要讨论的是强制性换道。
2.1 换道时间段的定义
驾驶员在执行换道行为时分为两步,一是反应,二是执行。换道时间段的定义见图3。
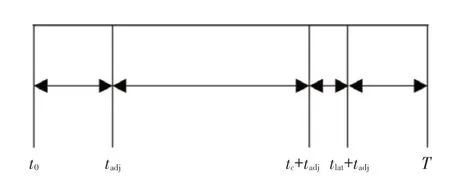
图3 换道时间区段定义
图3 中,t0为开始换道操作的时间,本文令t0=0;tadj为M 车施加横向加速度前的调整时间;tc+tadj为M车到达目标车道切线LS的时间;tlat+tadj为M 车施加横向加速度结束的时间;T为车辆完成换道的时间。
车辆施加横向加速度结束后,换道仍未结束,驾驶员根据目标车道前后车辆的速度,应迅速调整车辆速度,防止追尾事故。驾驶员选择换道(特指选择性换道),目的无非是在本车道舒适感不如目标车道,而表现舒适感的最重要因素是车辆的速度,因此,本车道的车辆在目标车道的速度应该大于在原车道的速度,且车辆在换道结束进行调整时,主车的速度因大于目标车辆后车速度,小于目标车辆前车速(理想情况下是,主车与前后车辆的速度差为零)。目标车道前车的速度为vLd,后车的速度为vFd(vLd≥vFd),假设主车在结束换道调整过程结束后,则主车的期望速度
2.2 换道过程中运动学分析及换道模型建立
换道过程中运动学分析见图4。
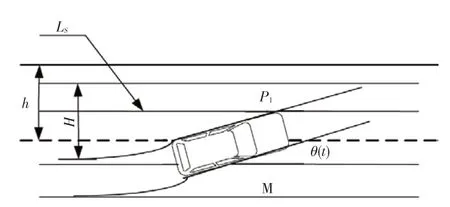
图4 换道的运动学分析
图4 中,LS为目标车道前导车右侧车道切线;P1与LS线相交点为已发生事故临界点。H为M车横向移动位移。图4描述的是主车M在换道过程的某一时刻的状态。以M 车的P1为参考点,换道的横向移动距离为H,且在H/2处,车辆的横向加速度alat(t) 达到最大。假设M 车在换道过程中运行平稳,Vlat(t)符合正弦波特性,则M 车的横向加速度alat(t) 符合余弦波特性。设:

其中,横向移动的时间到tlat+tadj截止,实际换道操作时间是tlat,则通过式(1)可以得到M 车左前角P1的横向移动位移,通过对加速度的积分可以得到:
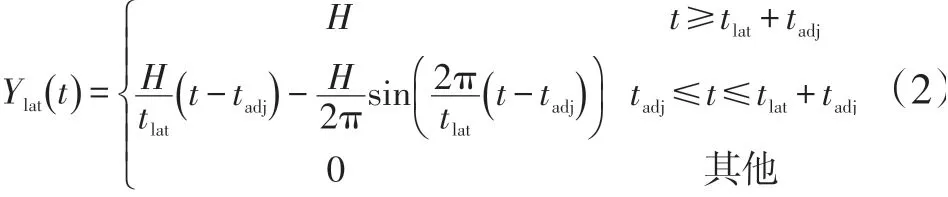
H的大小取决于驾驶员横向位置的选择,H=γh,γ值与驾驶员的特性有关。图4中θ( )
t表示主车t时刻行驶的轨迹切线方向与道路纵向的夹角,则有:
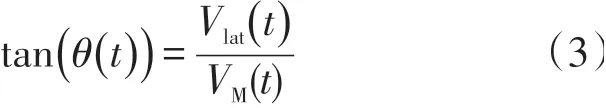
式中,Vlat(t)和VM(t)分别为车辆的横向速度和纵向速度。
对车辆换道的最小安全距离模型进行改进,主要体现车辆在采取换道行为时,并不是按照最小安全距离来进行换道,而是根据实际情况来改进模型的框架体系,使模型适应于任一道路。
M车和Ld车之间的安全距离如图5所示。
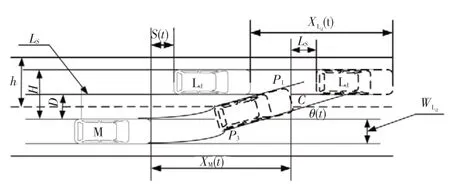
图5 M车和Ld车的安全距离示意图
根据图5,将所有形式的车辆碰撞考虑进去,要防止车辆碰撞则应满足:
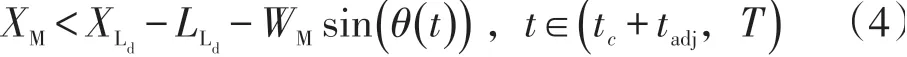
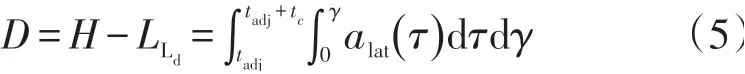
W的值能保证Ld车的P3点不被碰到。
3 换道过程中涉及的参数
根据式(4),容易得出tc+tadj>tlat2+tadj,即可得到,此时达到最大。
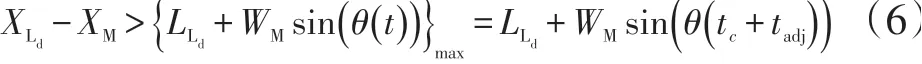
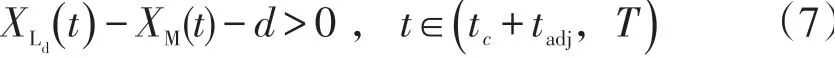
即可满足车辆不发生碰撞的可能。转化成方程:
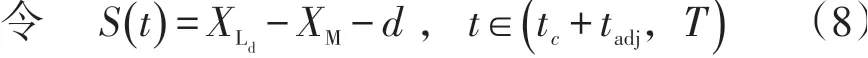
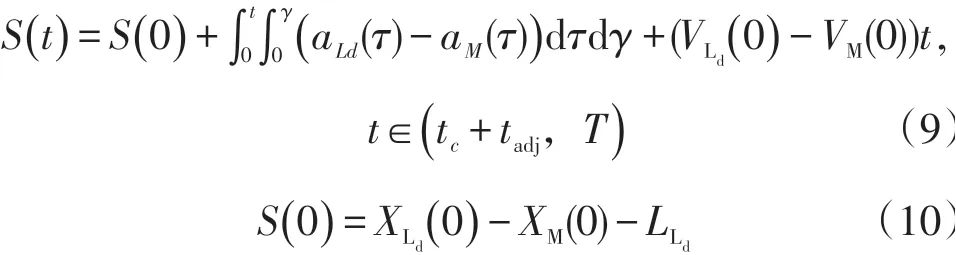
车辆平稳的换道过程对车辆、驾驶员及乘客的安全以及舒适度至关重要。车辆在换道过程所产生的曲率半径直接影响换道平稳性大小。图6 中L表示完成车道变化过程所需要的纵向距离:
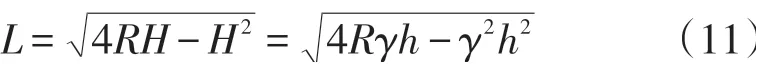
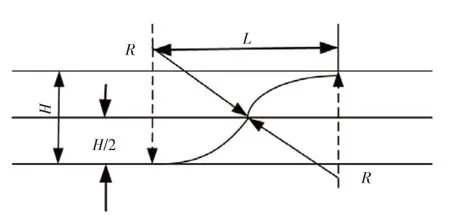
图6 换道过程的曲率半径
对于各国道路设计者而言,对R都有不同的设计标准,即车辆安全行驶时所必须满足的转弯半径。根据《公路工程技术标准》(JTG B01—2003)规定,当车速分别为120km/h、100km/h、80km/h、60km/h 时,极限最小半径分别为650m、400m、250m、125m。设Rmin为极限最小半径,则有:
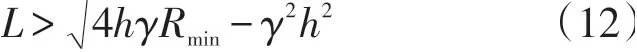
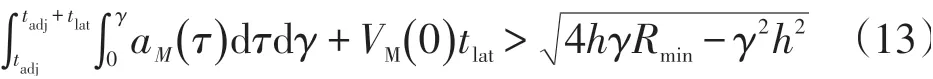
另有,Ls为换道结束后主车与前导车(跟随车)之间的距离,这与车辆之间的安全跟驰距离有关(在此不做讨论)。的大小与Ld(Fd)的速度、M 车的车速、车道横向间距H和时间tC+tadj有关。
当t=tc+tadj时,式(14)成立:
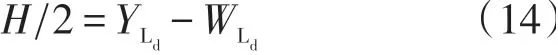
式中:YLd——前导车的横向坐标;
WLd——前导车的车宽。
结合式(2)、式(14)可以得到t1at与tc的数学关系式:
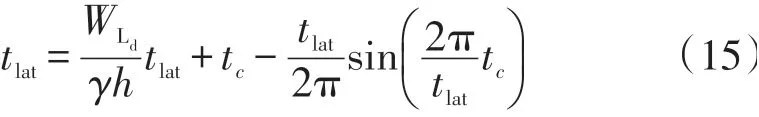
结合式(5)、(13)及式(15)可以基本上确定施加加速度tlat及tc的相对关系,并确定其与车道及车辆的宽度、主车的加速度及速度及驾驶员的特性有关系。
4 结语
本文所建立的数学模型考虑了车辆在换道过程中需要考虑车辆与本车道前车,目标车道前车、后车速度的影响,考虑了驾驶员因素、道路宽度等的影响,从本质上反映了车辆在换道过程中的驾驶行为,可为道路指路标志设计提供指导,为驾驶员在换道决策中提供参考。但是本文也有一定的局限性,实际行车过程中影响车辆车速的因素很多(简单的可以考虑车辆是匀速或者匀变速运动行驶)。而且车辆的类别多种,本文未将其区别看待。车辆在车道内行驶的横向位置一般情况下都是沿车道中心线行驶,但是实际生活中车辆在车道线内的位置一般是由驾驶员的特性决定。总的来说,该模型考虑了人、车、路环境等一系列因素,比较全面地分析了换道行为的影响因素,为换道决策提供了较为全面的理论基础。
[1] P Hidas. Modeling Lane Changing and Merging in Microscopic Traffic Simulation[J]. Transportation Research Part C,2002,(10):351-371.
[2] FHWA. FREESIM User Guide (4.5ed) [R]. Technical Report, Virginia: Federal Highway Administration, US-DOT,1994.
[3] 邓金城.汽车防撞系统中的危险估计与超车决策[J].计算机仿真,2004,(11):207-210.
[4] 王文霞.高速公路基本路段换道安全模型的研究[D].长春:吉林大学,2006.

