GM(1,1)模型在路基沉降预测中的应用

张 健

（如皋市交通投资发展有限公司，江苏 如皋226500）

（1,1）灰色模型在路基沉降预测中具有可行性。

0 引言

随着我国经济建设的蓬勃发展，普通公路已经无法满足人们出行的要求，高速公路建设日益增多。而路基沉降是影响高速公路工程质量的最重要的因素。因此，如何准确及时根据施工的实测沉降观测资料来对后期沉降进行预测，已经成为沉降动态控制的关键。

目前的沉降预测方法主要分为两种：理论法和数字方法。前者是通过土的固结理论，结合不同土的本构模型，采用一定的数值计算方法来实现的。但是，由于土体具有区域性、复杂性，工程数据不一定完全符合实际，需要的计算参数很多，一般需要通过三轴固结试验来确定，因此，很难将理论法普遍应用于实际工程中。后者利用实测工程沉降观测数据，将沉降近似看成符合某种规律变化的过程，建立与其相适应的模型，通过适当的优化方法，由此反算出计算公式所需要的参数，建立沉降与时间的关系式，再将其运用于后期的沉降预测。目前，主要的数学方法有：三点法、星野法、Asaoka 法、曲线拟合法、灰色模型法、人工神经网络法和遗传算法[1]。

由于灰色模型法需要的样本数量少，不需要有明显的规律性，计算工作量小，精确度高，因此，基于灰色理论的灰色模型在公路路基沉降预测中得到了普遍的应用。

本文运用灰色系统理论，把路基沉降过程看成是一个灰色系统，建立路基沉降的灰色模型以分析其沉降的发展变化，并结合某高速公路路基沉降观测的实测数据，用非等时距GM（1,1）灰色预测模型分析对比了实测数据与预测数据，结果表明该模型在路基沉降预测中是可行的。

1 灰色模型的建立

灰色预测模型又称GM（Gray Model）模型，它揭示了系统内部事物连续发展变化的过程。灰色模型是利用系统部分已知信息，建立起反映系统发展规律的微分数学模型，并通过建立的灰色模型来预测系统的发展。灰色系统理论的基本思路是：首先对数据进行累加处理（1-AGO），使观测数据序列的随机因素影响淡化，从而提高观测数据序列的内在规律，然后再将数据序列建成一个变量，并建立微分、差分、近似指数规律兼容的灰色模型[2]。根据预测因子的数目可细分为一阶多元预测模型GM（1，N）和一阶一元预测模型GM（1,1）。目前GM（1,1）模型应用较多，因此，下面主要讨论GM（1,1）模型的建立过程及其在工程上的应用[2-3]。

1.1 GM（1,1）模型的建立

给定原始序列，记为：

对（1）做一次累加可生成1-AGO序列：

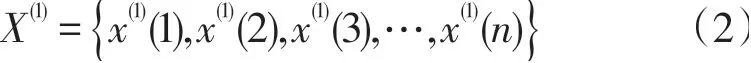
建立GM（1,1）模型的白化方程为：

式中，参数a反映了系统发展的姿态，成为发展系数；参数b是从背景值挖掘出来的数据，反映数据变化的关系，称为灰色作用量。根据最小二乘法原理，解式（1）可得发展系数

则白化方程的解为：

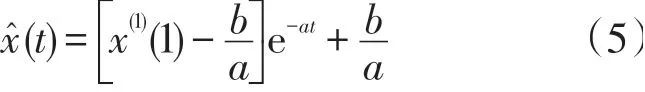
最后通过累减实现序列还原，还原值为：

1.2 模型精度的检验

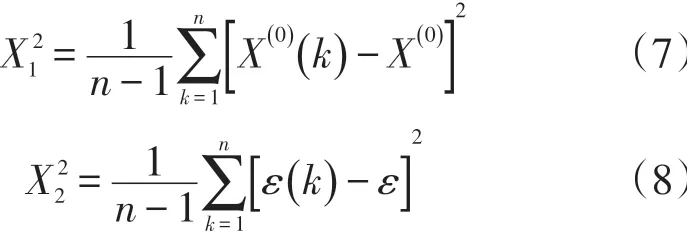
式中，σ为概率函数；ε(k)为残差序列的第k项。指标C越小，说明残差方差小，原始数据方差大，此时残差比较集中，摆动幅度小；P越大，越说明残差与残差均值差的绝对值小于给定值的点较多。所以C越小，P越大，其预测精度越高。参照P与C的大小，可将精度分为4 个等级[4]，具体如表1所示。

表1 GM（1，1）模型精度等级参照表

2 工程实例

现以某高速公路K191+240、K191+300两个断面的观测数据验证GM（1，1）模型在路基沉降预测中应用的可行性。这两个断面的实测数据见表2。

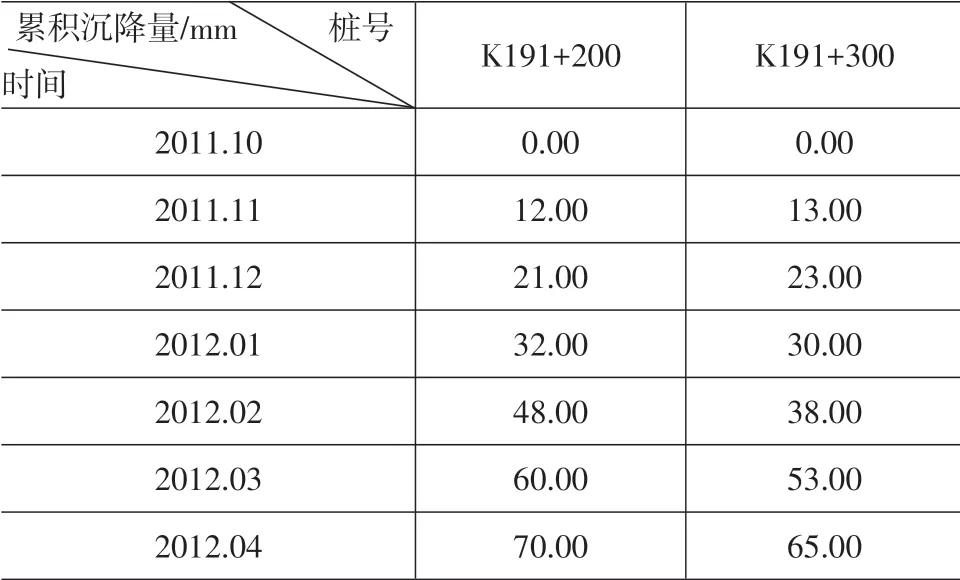
表2 沉降观测数据

根据以上实测数据，建立GM（1,1）模型。对K191+200、K191+300 断面分别进行计算和预测，结果如表3、表4所示。

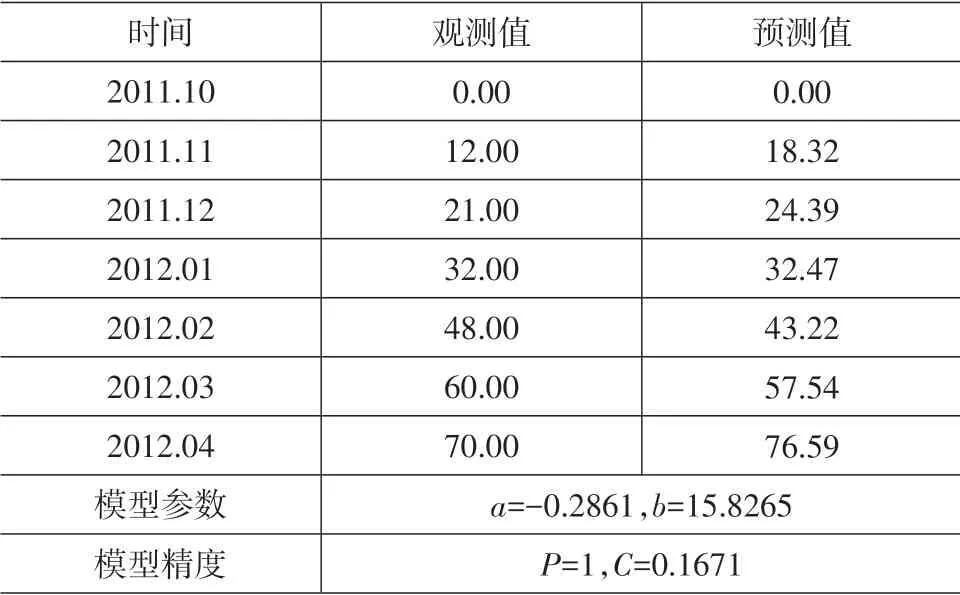
表3 K191+200断面预测结果

表4 K191+300断面预测结果

由表3、表4 可知，K191+200 断面P=1，C=0.1671；K191+300 断面P=1，C=0.081。根据模型精度等级参照表，可以看出模型精度均为良好，能够满足工程实际的需要，不需要再用残差模型进行修正。

4 结论

由上述分析得出如下结论：

（1）GM（1,1）灰色模型建模简单，所需要的数据较少，用该模型预测路基的沉降可靠性较好，预测精度高；

（2）利用GM（1,1）灰色模型对路基沉降进行预测，对路基的施工具有一定的指导意义；

（3）选择的实测数据的个数对GM（1,1）灰色模型的预测结果会造成一定的影响，还需要深入研究。

[1] 王星华，吴汉波，祝志恒.神经网络在填石路基沉降预测中的应用[J].路基工程，2008，（3）：12-14.

[2] 雷学文，白世伟，孟庆山.灰色预测在软基沉降分析中的应用[J].岩土力学，2000，21（2）：145-147.

[3] 王寒梅，唐益群，严学新，等.软土地区工程性地面沉降预测的非等时距GM（1，1）模型[J]. 工程地质学报，2006，14（3）：398-400.

[4] 李日云，王力，张双成.灰色预测模型在高层建筑物沉降预测中的应用研究[J].地球科学与环境学报，2005，27（1）：84-87.