基于层次分析法的应急救援最优路径选择分析

张 慧

（重庆交通大学交通运输学院，重庆400074）

0 引言

应急救援系统中最重要的问题之一就是如何使救援车辆在最短时间内到达事故现场，这就涉及到应急救援系统中最短路径选择问题。相关资料表明，高效的应急救援系统可以将事故损失降低到无应急系统的6%[1]。而最短路径不仅仅指一般意义上的距离最短，还可以引申到其他的度量，如时间、费用、线路容量、路况等。传统的最短路径算法主要有Dijkstra算法和Floyd算法。前者用于计算一个节点到其他所有节点的最短路径，后者是用于计算所有节点之间的最短路径。但这两种算法的时间花费很大。Dijstra 算法对于有k个节点的图，计算一个节点到其余节点最短路径的算法时间复杂度是O（k2）。

由于最短路径算法的复杂性，国内外许多学者对此进行了大量的研究。文献[2]根据起始点和终止点的方向，在最短路径计算中限制了一定的方向，减少了计算时间。文献[3]以要计算的最短路径的起始点和终止点为焦点，画出一个椭圆，最短路径的计算限制在这个椭圆中。在这些算法中增加了一些约束条件，使得最短路径解并不一定是精确解。本文在传统的Dijkstra 算法基础上结合实际的交通情况提出了一种新的算法称为最优路径算法，主要思想就是应用Dijkstra 算法探索了应急救援新的路径权重计算方法，提出一套最优路径决策方法。

1 最短路径算法的实现

最短路径问题的求解方法主要有Dijkstra 标号法、灰色理论、蚁群算法、Floyd 算法、遗传算法等。本文根据解决应急救援最优路径问题的需求，应用MATLAB 仿真，以Dijkstra 标号法为基础，求解应急救援最优路径选择问题。

1.1 Dijkstra算法原理

Dijkstra 算法是图论中求解最短路径的一个著名的算法，用于求图中一个节点到其他各个节点的最短路径。将道路抽象为网络中的边，以边的权值来表示与道路相关的参数，权是广泛的，可以表示速度、天气情况、交通情况、距离等。最短路径的衡量是通过计算路径的边权来决定的，所以边的权值都是非负数。网络中所有节点初始化为未记节点，在搜索过程中和最短路径中的节点相连通的节点设置为临时标记节点，每次循环都是从临时标记节点中搜索距源点最短的路径长度的节点标记为永久标记节点，直到所有节点或目标节点都成为永久标记节点，算法结束。

1.2 Dijkstra算法的实现步骤

假设每个点都有一堆标号（dj，pj），其中dj是从起源点s到点j的最短路径的长度（从顶点到其本身的最短路径是零路（没有弧的路），其长度等于零）；pj则是从点s到点j的最短路径中点j的前一点。求解从起源点s到点j的最短路径算法的基本过程如下。

（1）初始化，起源点设置为：

①ds=0，ps为空；

②所有其他点：di=$，pi=？；

③标记起源点s，记k=s，其他所有点设为未标记的。

（2）检验从所有已标记的点k到其直接连接的未标记的点j的距离，并设置：

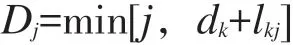
式中，lkj为从点k到j的直接连接距离。

（3）选取下一个点，从所有未标记的结点中，选取dj中最小的一个i：di=min[di，所有未标记的点j]，点i就被选为最短路径中的一点，并设为已标记的。

（4）找到点i的前一点，从已标记的点中找到直接连接点i的点j*，作为前一点。

（5）设置：i=j*，如果所有点已标记，则算法完全退出；否则，记k=i，转到第（2）步再继续。

2 建立层次模型

每个因素对寻求最优路径的影响不一样，也就是各自所占权重不一样。各层指标权重的确定是最优路径选择的关键的一个步骤，直接影响救援效率。确定指标权重的方法有很多种，包括层次分析法（AHP法）、德尔菲法、熵权法和模糊聚类分析法等。相对于其他方法，AHP 法不需要具备样本数据[4]，专家仅凭对评价指标内涵与外延的理解即可作出判断，且结合了定量分析和定性分析，可以把定性分析的结果量化。另外，AHP 法的使用范围比较广泛，且简单易行。因此，本文采用层次分析法来确定各指标的权重是比较适合的。

2.1 建立层次结构模型

AHP 法首先把问题层次化，按照问题性质和总目标将此问题分解成不同层次，构成一个多层次的分析结构模型。本文将层次结构分为三层（见图1）。目标层A计算路径权重，准则层B是影响权重的因子，方案层C是关于道路的使用功能。任务和交通量等分为5个等级，由高到低分别为道路1、道路2、道路3、道路4、道路5。

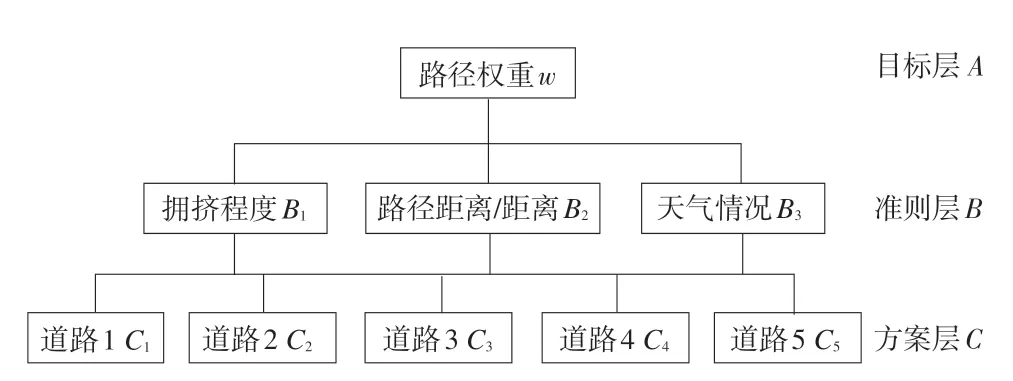
图1 路径权重层次结构模型

2.2 权重值的解算过程

先利用层次分析法对准则层各指标对于目标层的权重进行计算，再用层次分析法对方案层各指标对于准则层的权重进行计算。步骤如下：

（1）构造判断矩阵。构造下层各因素对于上一层准则的两两比较判断矩阵，依据表1 进行取值。

表1 1-9标度的含义

（2）完成所有的两两比较，计算权重，权重的计算方法有根法、合法、对数最小二乘法、特征根法。本文选用特征根法：

式中，Kmax是A 的最大特征根；W是特征向量，且归一化后就可作为权重向量。

（3）计算一致性比例CR，它表明判断矩阵偏离可靠性的程度，计算方法如下：

式中，CI为一致性指标，CI=（Kmax-n）/(n-1)；RI为平均一致性指标，取值如表2所示。

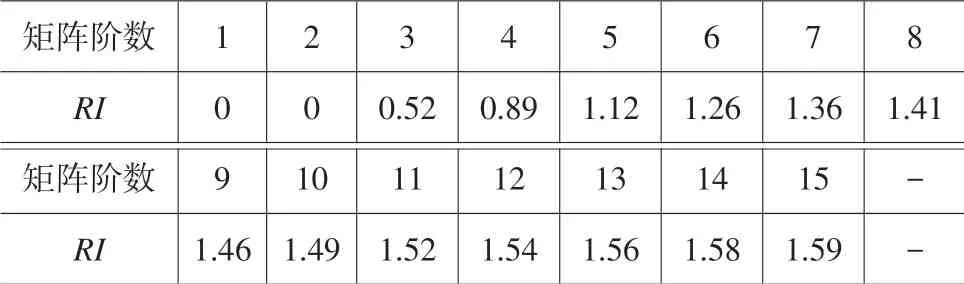
表2 平均一致性指标RI

当CR＜0.1 时，判断矩阵一致性是可靠的；当CR≥0.1时，必须对判断矩阵作修正。

（4）各层都完成第（1）、（2）、（3）步的计算。

（5）层次合层计算。

（6）整个层次进行整体一致性检验。不通过就对部分判断作适当的改善，使其满足一致性检验标准[5]。

建立各层对目标层的判断矩阵，如表3所示。

表3 准则层对目标层的判断矩阵

运用MATLAB 软件求得判断矩阵A 的最大特征值Kmax=3.0940，对应的归一化特征向量为W（2）,其值见表3。

CI（2）=0.047＜0.1；CR（2）=0.09＜0.1 满足一致性检验标准。表明A通过一致性检验，各个指标的权重系数为归一化的特征向量。

建立方案层对准则层B1的判断矩阵，如表4所示。

表4 方案层对准则层B1的判断矩阵

运用MATLAB 软件求得判断矩阵B1的最大特征值Kmax=5.0681，对应的归一化特征向量为其值见表4。性检验标准。

方案层对准则层B2的判断矩阵，如表5所示。

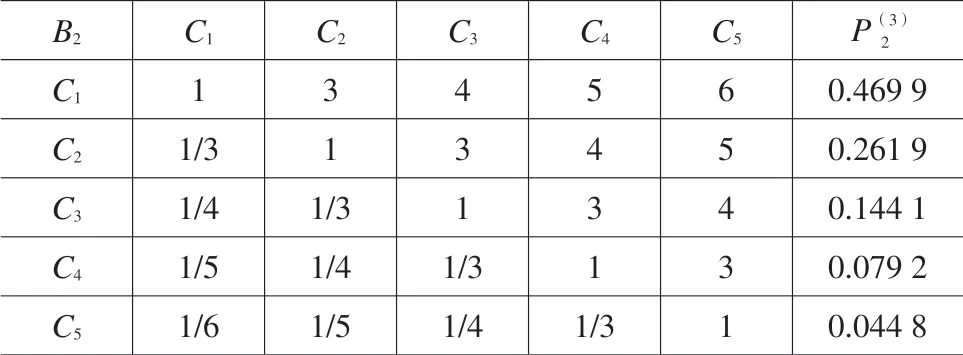
表5 方案层对准则层B2的判断矩阵

运用MATLAB 软件求得判断矩阵B2的最大特征值Kmax=5.3136，对应的归一化特征向量为其值见表5。性检验标准。

方案层对准则层B3的判断矩阵，如表6所示。

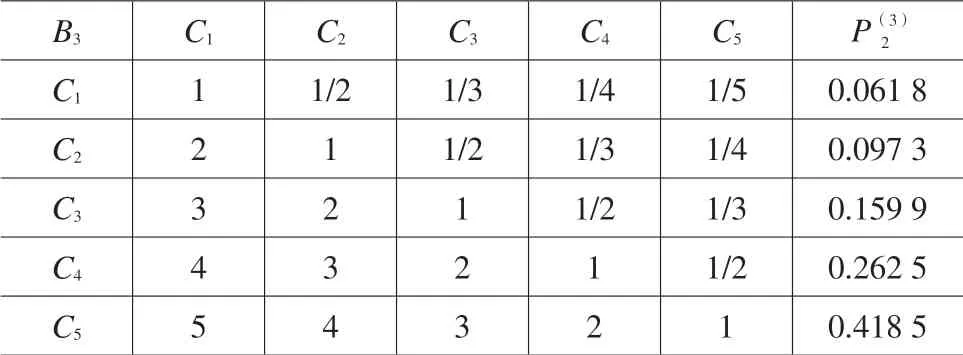
表6 方案层对准则层B3的判断矩阵

运用MATLAB 软件求得判断矩阵B3的最大特征值Kmax=5.0681，对应的归一化特征向量为其值见表6。致性检验标准。

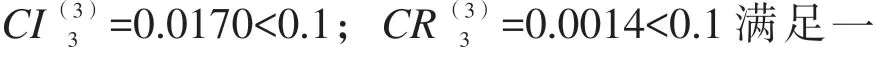
C层对A层的总排序如表7所示。

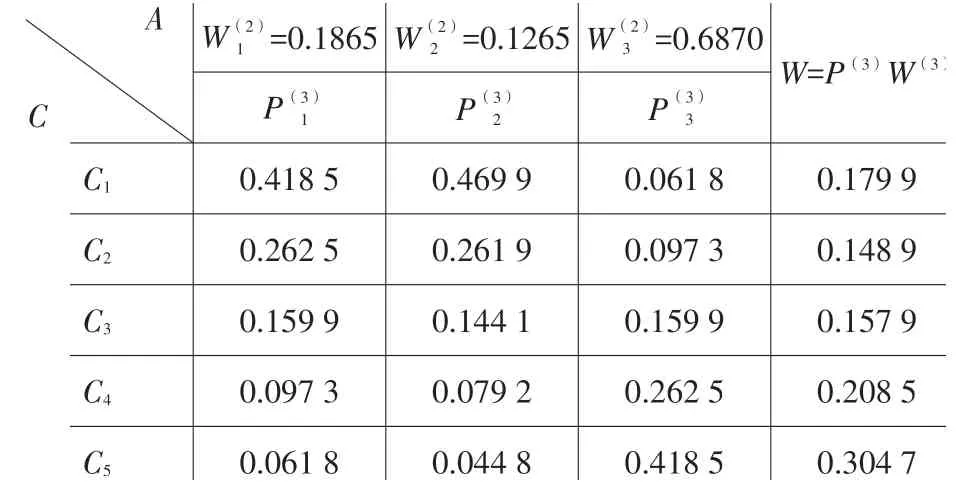
表7 C层对A层的总排序

C层对目标层的一致性检验：故满足一致性检验要求。表明C通过一致性检验，各个指标权重系数为归一化后的特征向量。

3 最优路径仿真实验

图2为某地区发生一起交通事故后，医院到救援事故点的路径情况。其中V1表示医院，V5表示事故发生点。通过上述计算，可以获得各影响因子的权重值，然后利用式（4）计算路径权值。其中整个网络图中各路径的s/v取相同单位，最终对路径权重W进行等值的无量纲处理。

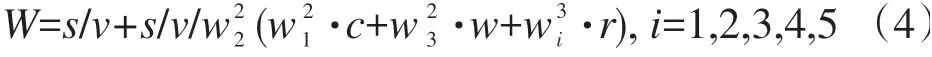
表8 该地区的各参数取值

将表8中的各数据代入式（4），可得到每个路径的取值（见图2）。

运用Dijkstra 算法在MATLAB 软件中实现，可求得医院到事故的最短路径为：V1—V2—V5，最短路径长为2.5。

4 结语

在研究各种最短路径算法的基础上，选用经典的Dijkstra 算法作为最优路径选择的基础，运用层次分析法计算应急救援道路的权值影响因子系数，提出一种路径权值的计算方法，并运用MATLAB计算仿真，验证整套方案的可行性。这个方案在一定程度上能提高应急救援决策的效率，但是该方法对各路径权重的确定的合理性仍需实践的进一步检验。

[1] 李志宪.事故应急救援预案范例精选[M].北京：煤炭工业出版社，2007.

[2] 严寒冰，刘迎春.基于GIS的城市道路网最短路径算法探讨[J].计算机学报，2000，（2）：210-215.

[3] 陆峰，施晓东，朱大奎.GIS中使用改进的Dijkstra算法实现最短路径的计算[J]. 中国图形图象学报：A 辑，1999，（10）：1019-1023.

[4] 王靖，张金锁.综合评价中确定权重向量的几种方法比较[J].河北工业大学学报，2001，30（2）：52-57.

[5] 同济大学出版社. 线性代数[M]. 成都：四川大学出版社，2003：25-29.