基于两种包络面的机械制造业技术效率评价

逄红梅，唐晓华

（1．辽宁大学 经济学院，辽宁 沈阳 110136；2．沈阳工业大学 经济学院，辽宁 沈阳 110870）

基于两种包络面的机械制造业技术效率评价

逄红梅1，2，唐晓华1

（1．辽宁大学 经济学院，辽宁 沈阳 110136；2．沈阳工业大学 经济学院，辽宁 沈阳 110870）

为更客观评价制造业的技术效率，运用最优和最劣两种包络面的数据包络分析（DEA）模型分别对选取的2012年85家机械制造业上市企业的技术效率进行了测算，并运用几何平均法组合对两种包络面结果进行了合理化排序。研究结果表明：最优效率或最劣效率与组合效率排名存在偏差，利用组合排序结果更具有客观性；投入要素总量越小、波动幅度越大或者投入变量差额比越大，组合效率相对最优效率和最劣效率的排名变化幅度越大。基于以上结论，建议上市企业应该强化要素投入的均衡性和提高要素的利用率。

技术效率；数据包络分析；最优面；最劣面；机械制造业

2010年我国在机械制造业领域超过美国，成为全球制造业第一大国。然而面对越来越激烈的市场竞争，机械制造企业生产增速在减缓［1］，成本优势逐渐弱化，而且制造业的负外部效应——能源与资源消耗逐渐显现，2011年国际统计年鉴显示，中国创造了世界9%的GDP，却消耗了世界11%的原油、62%的煤炭。因此作为我国重工业之首的机械制造业在高能耗与低效率方面矛盾突出，使投入产出达不到最优比例，鉴于此，本文从技术效率方面关注我国机械制造业。

从有关技术效率的研究动态来看，其分析方法主要有参数方法和非参数方法。常用参数方法是随机前沿分析（SFA）法，相对于数据包络分析（DEA）法，SFA方法考虑了随机误差，但是提前假设生产函数具有主观性，对效率值的评价存在影响。非参数方法最典型的是DEA法，它不用事先假设生产函数，参数估计的合理性与客观性更强，因此得到广泛应用。但是DEA方法没有考虑随机误差，另一个重要问题是无法区分有效率或完全无效率（效率值为1）决策单元的高低，即无法对有效率或完全无效率的决策单元进行充分排序。为此，国外学者衍生出多种基于最优面的 DEA 模 型，如 Super效 率 法［2－3］、Cross 效 率法［4］等，也相继提出基于最劣面的DEA效率评价方法，实现反向排序问题［5－6］。近年国内学者也尝试对DEA模型进行改进或者是采用不同的综合评价方法进行充分排序：刘永春等［7］运用DEA优势效率模型和劣势效率模型对工业生产效率进行测评，然后主观选择优势效率值与劣势效率值的权重进行综合评价与排名；汪旭晖等［8］在CCRDEA和BCC－DEA的基础上提出超效率CCRDEA模型对我国24家物流上市公司的效率进行评价，在一定程度上解决了对有效决策单元不能充分排序的问题；段婕等［9］运用改进的DEA模型评价我国2007—2009年装备制造业7大类行业的技术创新效率水平，解决了决策单元数过少而不能对其进行有效评价和区分的问题。此外，卞亦文等［10］、毕功兵等［11］、李兆琼等［12］也从理论角度探讨了基于两种包络面的DEA模型不能对决策单元充分排序的问题，并在理论支撑下提出各自的综合方法，进行合理排序。这些文献从理论研究和实际应用两个方面对有效或完全无效决策单元再排序问题进行了分析，但是当前应用基于两种包络面的DEA方法对上市机械制造业企业技术效率评价的研究还比较缺乏，特别是缺乏对制造企业的合理排序以及技术效率差异分析［13］。

本文将利用D E A最优面模型和最劣面模型分别测算8 5家机械制造业上市企业技术效率，运用几何平均法组合两种包络面的效率值，客观评价我国机械制造业上市企业的技术效率水平，分析三种效率值的差异原因及提出相应改进措施。

一、研究方法

D E A模型有多种具体应用模型，而最优面和最劣面模型属于标准模型，由于本文分别采用两种模型来计算样本数据的技术效率，因此首先介绍上述两种模型，然后介绍本文采用的最优与最劣效率值组合方法——几何平均法，为机械制造企业的技术效率进行有效排序提供理论基础。

1．最优面模型

设有n个具有可比性的决策单元（简称DMU），每个DMU有m种输入指标和s种输出指标，第j（j＝1，2，…，n）个DMU的第i（i＝1，2，…，m）种投入记为xij，第r（r＝1，2，…，s）种产出记为yrj，μr和vi是对应的产出投入指标权重，则建立基于最优面的D E A－C C R模型如下：

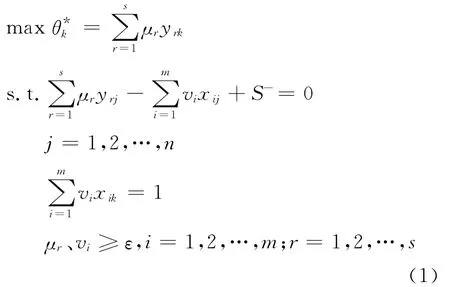
式（1）中S－为与投入指标相对应的松弛变量向量；ε是非阿基米德无穷小数①早在1 9 5 2年C h a r n e和C o o p e r研究使用单纯形法求线性规划的最优解时，在“退化”情况下可能出现“循环”现象，他们引进非阿基米德无穷小ε的概念。，决策者根据需要选取。如果存在一组非负权重使θ＊k＝1，那么定义DMUk为D E A有效，否则DMUk为非D E A有效，有效DMU构成的面为最优前沿面。

2．最劣面模型

利用式（1）进行效率测算时，对非D E A有效DMU可以充分排序，但是对于效率值为1的多个DMU视为无差异，因此无法进行有效排序，这也是传统D E A－C C R的缺陷之一。在此基础上引进了基于最劣面的D E A模型，且由完全无效DMU构成的面称为最劣前沿面。

根据以上要求，构造最劣面D E A模型如下：

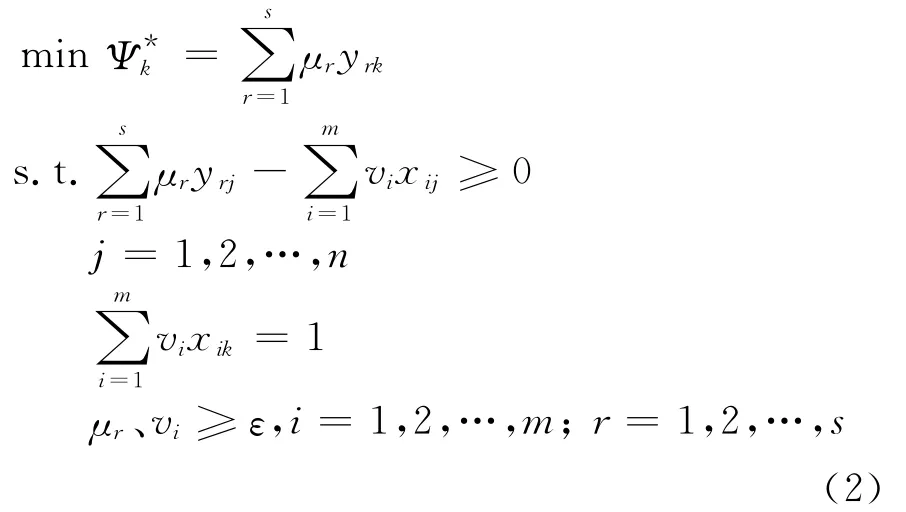
如果存在一组非负权重使＝1，那么称DMUk为完全无效，表明DMUk已处在最劣前沿面上，是最无效的。若≠1，则称DMUk为非完全无效。值越大说明DMUk离最劣前沿面越远，表明该DMUk越有效。与式（1）相反，式（2）可以有效地区分有效DMU，但却不能区分完全无效DMU。

3．最优面与最劣面相结合

基于式（1）和式（2）不能对DMU进行充分排序的缺陷，本文综合考虑两种包络面结果，使DMU能充分排序，在实际应用中更具有说服力。本文选取W a n g提出的几何平均法进行组合［14］。

对于第k个决策单元DMUk的最终效率值为：

二、指标选取与数据收集

1．指标选取

“十二五”规划中明确指出发展现代产业体系，促进我国制造业由大变强，使其高端化。虽然我国目前是全球第二大经济体，但是作为国民经济的重要支柱性产业，制造业存在投入冗余、产出不足、资源利用和技术创新等诸多低效率问题。鉴于此，本文选择评价我国机械制造业上市企业的技术效率水平，以达到在现有技术水平下，获得最大产出或最小投入的能力，从而正确认识各企业利用现有资源和技术的有效程度。

在利用DEA方法评价技术效率时，投入产出指标多数依照Solow余值法，选取以价值衡量的总产值（或增加值）为产出指标，以价值表示的资本和以人数表示的劳动力作为要素投入指标［15－22］。指标选取是否合理直接影响测算结果，所以要求指标必须能客观真实地表述研究样本的特点和技术效率评价要求。本文样本数据是上市公司数据，考虑到上市公司披露的基本都是财务数据，并结合我国制造业上市公司投入和产出特征以及现有数据的可获得性，选取如下投入指标。①计算投入变量差额比时投入产出指标原始数据中负值已作相应处理，即各DMU的同一指标数据同时加上或者减去相应的正数来抵消负数，DMU的有效性不变。总资产：表示公司的总体经营规模，是实现经济效益的物质保障，也是提高公司产出规模的关键要素，侧面反映上市公司的成长速度。②因投入变量均采用统一计量单位（人民币：百万元），所以采用均值可以解释企业投入变量冗余的总体情况。经营活动产生的现金流量净额：是公司是否具有扩大再生产的能力和是否值得投资的重要标杆。③最优效率值全部小于或等于1，最劣效率值全部大于或等于1，这是式（1）和式（2）的自身结构特点决定的，式（1）是在保证产出不变时，尽量减少投入，使效率值尽量接近有效单元（效率值为1），因此效率值小于1；式（2）是在保证产出不变，投入尽量减少，使效率值远离最劣面上的无效单元（效率值为1），因此效率值大于1。营业总成本：是反映公司利润增长和对资产利用水平的主要因素。本文选取如下产出指标。①营业总收入：代表上市公司产出规模，与营业总成本相匹配，反映公司是否具有可持续发展的能力。②净利润：是反映公司绩效的重要指标，也从侧面体现公司管理水平的高低和发展潜力。

由于数据限制，难以找到与劳动力人数相匹配的指标数据，所以本文只从实际数据可获得性考虑，采用上述投入产出指标，前人相关文献［23－26］也验证了上述指标使用的可行性和研究结果的可靠性。

2．数据收集

本文按照中国证监会的行业分类标准，选择在沪深两市A、B股上市的普通机械制造业企业为研究对象，2012年末共涉及86家企业，本文剔除数据不全的东方锅炉，最终采用85家企业对其分析。利用CSMAR数据库收集指标数据，表1列出了各变量的描述性统计特性。

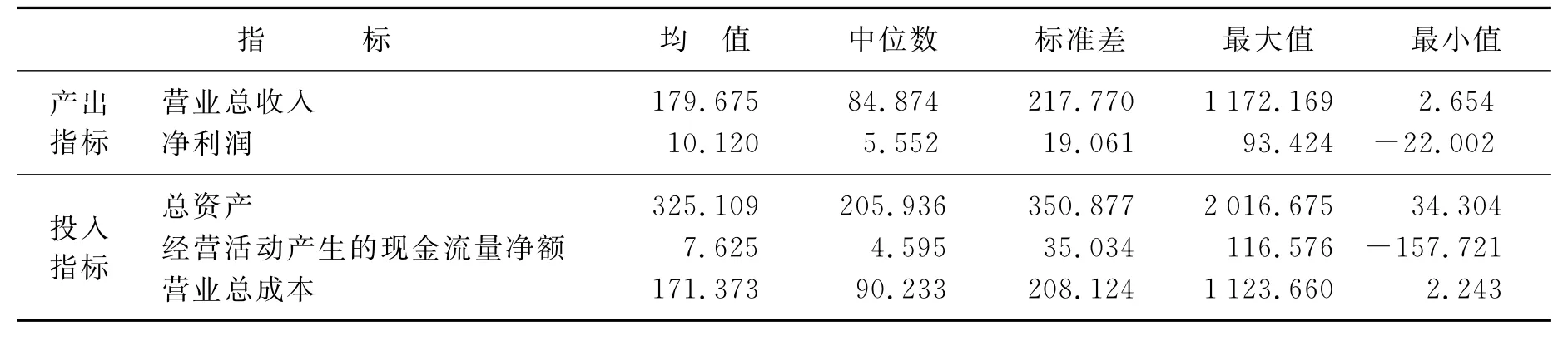
表1 各变量的描述性统计特性 单位：百万元

三、实证结果与分析

1．实证结果

本文采用Matlab软件为数据分析工具，将85家上市公司的投入产出原始数据利用式（1）和式（2），分别计算出各个上市公司的最优效率值、最劣效率值，然后通过几何平均法得到组合效率值与排名，同时列出利用式（1）计算的各投入变量差额比①，因篇幅所限，仅列出投入变量差额比的均值②，如表2所示。

2．基本结果分析

从表2的最优效率均值（0．886）和最劣效率均值（1．417）来看③，85家企业中分别有46家和42家企业处于相应均值之上，说明利用最优面模型和最劣面模型评价技术效率存在不一致性。首先，通过最优面模型计算的最优效率值可以对无效的DMU进行排序，其中银星能源、东力传动、洪城股份、新筑股份和华东数控5家企业排名最差，对沈阳机床、开山股份、日发精机、杭锅股份、汉钟精机、汇通能源等13家效率值为1的企业不能进一步排序，因此无法区分有效企业孰优孰劣。其次，通过最劣效率值同样可以发现对效率值较高的开山股份、日发精机、龙源技术、隆华节能等企业可以排序，而对效率值为1的＊ST天一、廊坊发展、湘电股份和华东数控4家企业无法排序。最后，应用式（3）组合式（1）和式（2）的结果，发现同时考虑最优和最劣两个效率值可以对各企业进行充分排序，结果表明开山股份效率最高，其次是日发精机、龙源技术和汉钟精机，效率最差是洪城股份、新筑股份和华东数控等企业。

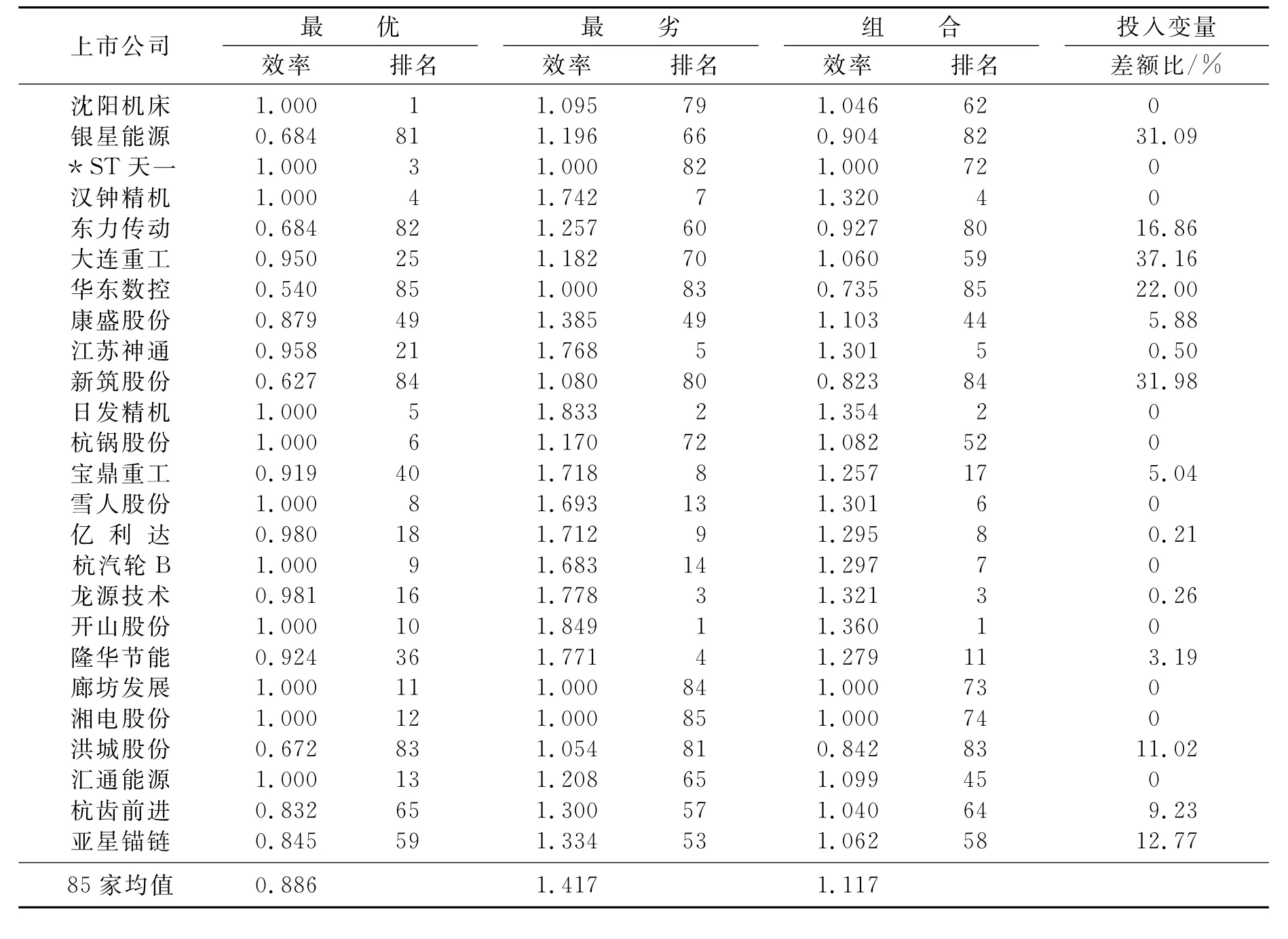
表2 技术效率测算结果与投入变量差额比均值

然而从各企业三种效率排名上看，组合排名结果与最优效率、最劣效率排名相比，存在较大偏差。利用式（1）计算最优效率值时，沈阳机床、＊ST天一、杭锅股份、廊坊发展与湘电股份排名并列第1（效率值均为1），但是组合效率分别排第62、72、52、73和74名；相反龙源技术、隆华节能、江苏神通与宝鼎重工最优效率排名分别为第16、36、21和40，而组合排名上升至第3、11、5、17名。这种情况表现一个共同特征是：同一企业的优势效率与劣势效率排名差距很大，即该企业优势突出，劣势也同样明显，或者优势不明显，劣势也不突出，说明单一从某一角度均不能准确评价企业技术效率水平，此时组合效率值更具有说服力。若企业最优效率与最劣效率排名比较接近，组合后的排名变化幅度也不大，如康盛股份、亚星锚链、杭齿前进等企业的最优效率值和最劣效率值能相对准确反映其投入产出水平。经分析，组合效率可比性大大增强。

3．组合技术效率差异性分析

通过以上分析可知，采用组合效率结果评价企业利用资源水平具有相对合理性，但是85家上市企业中有39家企业处于组合效率均值（1．117）之上，技术效率最高与最低的企业之间相差62．5个百分点，这种差异性是由多方面决定，一方面体现在如政府政策、经济环境、地域优势、资源优势等外在因素上，另一方面体现在企业自身投入与资源利用效率等方面。针对本文的研究内容，为更好解释最优效率、最劣效率与组合效率的差异性，从而更详尽分析技术效率差异，这里仅从投入资源利用率（用投入变量差额比来表示）和原始投入总量来具体分析①由于篇幅限制，本文分析所采用的三种投入变量差额比与原始投入总量不具体列出。这里差额比只列出平均值，可以解释总体冗余情况。，见图1。

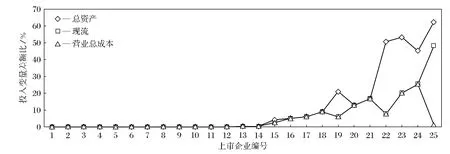
图1 上市公司三种投入要素冗余情况

图1显示的是85家上市企业①图1只显示85家上市企业中的25家企业，与表2中的企业对应，其中编排序号按照其投入变量差额比均值由低到高排列。中25家企业的总资产、经营活动产生的现金流量净额、营业总成本三种投入要素冗余情况，总体来看，总资产投入冗余最高，经营活动产生的现金流量净额与营业总成本投入冗余情况相当。85家上市企业存在三种状态：第一种是三种投入要素均不存在冗余，有18家企业，如开山股份等；第二种是三种投入要素冗余幅度一致，要素投入较为均衡，涉及36家，如龙源技术等；第三种是存在投入要素冗余且冗余幅度不一致，表现最明显的企业——大连重工。

这些不同状态从某种程度上表现出最优效率、最劣效率和组合效率值的变化差异，具体从表2和图1中的投入变量差额比均值来看，每个企业对资源利用水平存在较大差异，华东数控、银星能源、新筑股份与大连重工的投入变量差额比均值在20%以上，前三者无论最优效率排名、最劣效率排名还是组合效率排名均靠后，而大连重工因最优效率与最劣效率排名差异巨大，组合效率排名也较靠后，位列第59名，这说明投入变量差额比越大，组合效率水平越低下。相反，投入变量差额比越小，组合效率水平相对越高，如雪人股份、杭汽轮B、亿利达等企业。但是仅从投入变量差额比分析技术效率差异性，会存在一些企业即使投入变量差额比较小，甚至是0时，组合技术效率水平也不高，比如沈阳机床、杭锅股份、湘电股份、汇通能源、＊ST天一、廊坊发展，造成这种差异除了外在的最优效率和最劣效率排名巨大差异外，主要原因在：一是原始投入总量波动幅度较大，也就是说某一企业三种投入指标上相对来说存在较大波动性。例如沈阳机床在85家企业中“资产”、“营业总成本”两项投入指标均占第3名，但是“经营活动产生的现金流量净额”投入指标却占第84名，杭锅股份、湘电股份与汇通能源也存在类似情况。这是因为既定产出下，该DMU消耗的投入呈不均衡状态，形成评价最优效率时强调生产性能优势的一面，评价最劣效率时强调生产性能劣势的一面，各占优势的情况下，造成组合效率不高。二是原始投入总量均较小，即相对排名比较落后。代表性的企业如廊坊发展在85家企业中“资产”、“经营活动产生的现金流量净额”两项投入指标排名均倒数第1名，“营业总成本”投入指标也仅占第65名，＊ST天一也同理，因此组合效率水平也较低。

通过以上分析可以发现，无论是在投入要素利用水平，还是在原始投入总量及波动幅度上，都会影响最优效率和最劣效率的组合结果，所以防止单纯使用最优效率或最劣效率评价企业的片面性，利用组合效率能更客观地评价机械制造业上市公司的技术效率水平，便于决策者从多角度出发提升企业管理水平和经济效益，从而带动整个行业健康发展，像类似开山股份这样能达到最优的投入产出比和发展平衡的企业，可作为机械制造业的典范，而其他投入产出机制不合理的企业，需要适当调整资源投入总量和资源利用水平。

四、结论与启示

本文应用DEA两种包络面方法来测算85家机械制造企业的技术效率水平，为克服两种模型评价与排序缺陷，采用几何平均法组合两类效率值，使其决策单元充分排序与评价结果更符合实际。通过实证分析，得出以下基本结论：

第一，单纯利用DEA最优面模型或最劣面模型评价企业技术效率，都产生较大偏差，而利用组合效率值评价更能贴合实际，实证中有39家企业组合效率水平超过其均值，比超过最优效率均值的46家和最劣效率均值的42家少，表明了三种效率值之间的排序存在差异性，结果显示同一企业的优势效率与劣势效率排名差距越大，组合效率排名越靠后，反之，组合效率排名变化幅度越小。这说明上市公司可通过调整要素投入水平来改善资源配置，防止因要素“短板效应”而引起的组合技术效率低下，使其技术水平和资源利用得到充分发挥。

第二，从投入变量差额比、原始投入总量与波动幅度方面分析了组合技术效率内在差异性。结果显示：①投入变量差额比均值越大，组合效率越低，相反，组合效率越高。这说明上市公司应该加强投入要素转化实际生产力的能力，例如把相对较高总资产冗余转化为流动性较强的现金，可以通过固定资产处理、租赁等途径，提高资产使用效率，进而提升技术效率水平；另外可通过调整组织结构来提升管理能力，发挥隐性知识的重要作用来保证效率提升。②不符合上述判断标准的组合效率差异原因在于原始投入总量及波动幅度上，原始投入总量越小或者波动幅度越大，组合效率水平越低，反之，组合效率越高。这说明公司可以加大投入要素水平，进而增加产出规模，并保证投入要素在同行业中处于相对平衡的位置，使其最优效率与最劣效率评价都能达到自身最优水平，提高组合效率水平；或者上市公司进行产业转型升级，寻求创新发展，提升企业市场价值与资源利用水平。

通过利用几何平均法对最优效率和最劣效率的组合与排序、组合效率的差异原因分析，为提高技术效率，企业不仅应考虑在现有技术条件下的资源利用水平，还应考虑原始投入总量与投入平衡，才会利用最优效率或最劣效率相对准确地反映企业技术效率水平。另外还可结合制造业的实际情况，进一步挖掘影响企业技术效率的深层次原因，从而提供更有价值的参考对策。

［1］ 苏生荣．我国机械制造业现状与发展前景［J］．中国科技信息，2009（15）：155－158．

［2］ Andersen P，Petersen N C．A Procedure for Ranking Efficient Units in Data Envelopment Analysis［J］．Management Science，1993，39：1261－1294．

［3］ Tone K．A Slacks－based Measure of Super－efficiency in Data Envelopment Analysis［J］．European Journal of Operational Research，2002，143：32－41．

［4］ Sexton T R，Silkman R H，Hogan A．Data Envelopment Analysis：Critique and Extensions［C］∥Silkman R H．Measuring Efficiency：An Assessment of Data Envelopment Analysis．San Francisco：Jossey Bass，1986：73－105．

［5］ Jahanshahloo G R，Afzalinejad M ．A Ranking Method Based on a Full Inefficient Frontier ［J］． Applied Mathematical Modeling，2006，30：248－260．

［6］ Wang Y M，Yang J B．Measuring the Performances of Decision Making Units Using Interval Efficiencies［J］．Journal of Computational and Applied Mathematics，2007，198：253－267．

［7］ 刘永春，袁茂．基于DEA方法的中国工业效率研究［J］．生产力研究，2007（18）：103－105．

［8］ 汪旭晖，徐健．基于超效率CCR－DEA模型的我国物流上市公司效率评价［J］．财贸研究，2009（6）：117－124．

［9］ 段婕，刘勇，王艳红．基于DEA改进模型的装备制造业技术创新效率实证研究［J］．科技进步与对策，2012，29（6）：65－69．

［10］ 卞亦文，许皓．基于虚拟包络面和TOPSIS的DEA排序方法［J］．系统工程理论与实践，2013，33（2）：482－488．

［11］ 毕功兵，陶成，梁樑，等．基于权重集合的决策单元排序方法［J］．系统工程理论与实践，2010，30（12）：2237－2243．

［12］ 李兆琼，梁樑，夏琼，等．考虑两种包络面的熵DEA效率评价模型［J］．系统工程，2010，28（4）：68－73．

［13］ 王丽丽，赵勇．基于DEA的中国制造业效率评估［J］．山东大学学报：哲学社会科学版，2010（1）：32－39．

［14］ Wang Y M，Chin K S，Yang J B．Measuring the Performances of Decision－making Units Using Geometric Average Efficiency ［J］．Journal of the Operational Research Society，2007，58：929－937．

［15］ 叶振宇，叶素云．东北地区制造业生产率变动分析：1993—2007年［J］．财经问题研究，2010（5）：30－35．

［16］ 徐盈之，赵豫．中国信息制造业全要素生产率变动、区域差异与影响因素研究［J］．中国工业经济，2007（10）：45－52．

［17］ 任娟，陈圻．中国制造业上市公司创新行为对企业技术效率的影响研究［J］．科技进步与对策，2011，21（28）：80－86．

［18］ 李春顶．中国制造业行业生产率的变动及影响因素——基于DEA技术的1998—2007年行业面板数据分析［J］．数量经济技术经济研究，2009（12）：58－69．

［19］ 任娟．IT投资对我国机械制造业上市公司技术效率的影响分析［J］．技术经济，2011（5）：69－76．

［20］ 叶振宇，叶素云．要素价格与中国制造业技术效率［J］．中国工业经济，2010（11）：47－57．

［21］ 杨桂元，王莉莉．我国制造业技术进步、技术效率及区域差异——基于 DEA方法的实证研究［J］．技术经济，2008，27（1）：110－115．

［22］ 张庆芝，何枫，雷家骕．环境约束下的我国钢铁企业技术效率研究［J］．科学学与科学技术管理，2013，34（10）：103－111．

［23］ 赵旭．我国制造业上市公司技术效率与技术进步实证研究［J］．当代经济管理，2008，30（1）：60－67．

［24］ 路世昌，关娜．基于DEA－Tobit的装备制造业上市公司经营绩效研究——来自2005—2010年装备制造业的经验数据分析［J］．工业技术经济，2012（2）：108－115．

［25］ 苗敬毅，蔡呈伟．我国煤炭行业上市公司技术效率及其影响因素——基于Tobit－DEA模型［J］．技术经济，2012，31（7）：55－58．

［26］ 陈冰，吉生保．中国医药行业上市公司的绩效评价及影响因素——基于面板数据的DEA－Tobit实证研究［J］．中央财经大学学报，2013（8）：62－68．

Technical Efficiency Evaluation of Machinery Manufacturing Based on Two Envelopment Frontiers

PANGHong－mei1，2，TANGXiao－hua1
（1．School of Economics，Liaoning University，Shenyang 110136，China；2．School of Economics，Shenyang University of Technology，Shenyang 110870，China）

In order to more objectively evaluate the technical efficiency of machinery manufacturing，two data envelopment analysis（DEA）models（both the optimal and the worst）were applied for the first time to estimate the technical efficiency of 85listed machinery manufacturing companies of 2012，and by means of the geometric method the two envelopment frontiers results were reasonably sorted．The findings indicate that the optimal or the worst efficiency deviates from the combined efficiency in ranking，and the results are more objective when it comes to the combined efficiency；the fewer the input factors，the greater the volatility，or the more different the input variables are，the more differently the combined efficiency ranks as opposed to the optimal and the worst efficiency．Based on the above conclusions，listed companies are recommended to strengthen the balance of input factors and improve the efficiency of these factors．

technical efficiency；data envelopment analysis（DEA）；optimal frontier；worst frontier；machinery manufacturing

F 407

A

1008－3758（2014）01－0045－07

2013－08－10

国家社会科学基金重大资助项目（08＆ZD040）。

逄红梅（1978－），女（满族），辽宁岫岩人，辽宁大学博士研究生，沈阳工业大学讲师，主要从事产业经济及组织理论研究；唐晓华（1956－），男，广西桂林人，辽宁大学教授，博士生导师，主要从事产业经济研究。

王 薇）