基于卡尔曼滤波的轴向加速度动态误差补偿方法

杨慧娟，黄 铮，霍鹏飞，王 超

（1.中北大学 仪器科学与动态测试重点实验室，太原030051；2中北大学 信息与通信工程学院，太原030051；3.西安机电动态控制重点实验室，西安710065）

弹丸轴向加速度的精确测量在旋转稳定弹自主式射程修正引信研究中是一项关键技术，提高弹丸轴向加速度的测量精度对加速我国灵巧弹药技术的发展具有非常重要的意义。1982年Merhav S J研究了借助于旋转或振动加速度计三元组组成无陀螺的惯性测量组件，论述了从加速度计的输出信号中分离线加速度和角速度的方法［1］。1994年Chen发表了一种使用6个加速度计进行测量的新颖设计［2］。国内最早的报道见于文献［3］。

对于旋转稳定弹轴向加速度测量，由于弹丸在高速旋转时传感器具有横感特性，要求加速度传感器安装在弹丸对称轴，但安装误差总是存在的，微小的安装误差与弹丸的高转速环境相结合会导致很大的有害加速度输出。为了减小该项有害加速度，美国陆军研究实验室基于高速转台（300r／s）对加速度传感器进行标定，以得到转速与有害加速度之间的曲线关系，作为误差补偿的依据［4－5］。目前，在我国加速度计测量组合被广泛应用于常规火炮弹药的测速中，但在现有的文献中几乎都是理想条件下的测试，或者是没有考虑加速度传感器的安装误差及横感效应等对测试参数的影响，对加速度的动态补偿更是很少。

作者已有的研究成果［6］从理论上分析了弹载加速度传感器的输出与其在弹上的安装位置之间的关系，并在改进的质点弹道模型的基础上建立了弹丸轴向加速度模型，通过仿真验证了该模型的正确性。本文将在上述研究内容的基础上，通过卡尔曼滤波对轴向加速度进行动态误差补偿，以此减小加速度传感器在测量过程中输出的有害加速度，从而提高测量精度，实现旋转稳定弹轴向加速度的比较精确的测量。

1 动态补偿的基本问题

对于某一发确定产品，当弹丸上的加速度传感器安装好后，其安装位置引起的安装误差以及该加速度传感器本身引起的横轴灵敏度不再会发生变化。根据作者已有的研究成果［6］，轴向加速度的测量误差表达式为

从上述表达式可以看出，轴向加速度的测量误差与弹丸转速ω的平方成正比，且比例系数C是一个常数。当转速的测量精度比较高时，动态补偿就可以较好实现。

2 动态标定卡尔曼滤波算法

2.1 滤波状态方程

由于弹上标定环境特殊复杂，且要求实时性强，因此选取改进的质点弹道方程作为标定算法的状态方程［6－8］。

状态方程为

式中：v为速度，θ为弹道倾角，p为大气压强，ω为转速，c为弹道系数，C为需要估计的常数，Hτ（y）为空气密度函数，G（vτ）为阻力函数。

选取y，v，θ，ω，p，C为 状态变量，即：x＝（x1x2x3x4x5x6）T＝（yvθωpC）T。

则方程（1）可以写为

为了补偿线性方程（2）对炮弹质心运动的近似描述造成的误差，在此引入一个零均值高斯白噪声V，且V～N（0，Q′）。

状态变量的初值为

在具体仿真过程中某次状态变量的初值选取与本次改进的质点外弹道方程解算的初值相同，其中常数C0为一个确定的初值。

2.2 滤波量测方程

基于旋转稳定弹的改进的质点外弹道方程，结合轴向加速度的输出模型，仿真得到的加速度传感器输出值作为滤波过称中加速度传感器的量测值aact，通过仿真得到的转速作为滤波转速的量测值。

量测方程为

式中：Bs为加速度传感器的零点漂移。

在量测方程基础上加入量测噪声d，且d～N（0，R′）。

2.3 动态补偿滤波算法

卡尔曼滤波只适用于线性系统，而式（1）、式（4）都是非线性的，因此需要对非线性状态方程（1）、量测方程（4）进行线性化、离散化，由此得到卡尔曼滤波弹道方程［9］。

预测一步预测方程：

量测量的一步预测方程：

一步预测均方误差方程：

最优滤波增益方程：

估计均方误差方程：

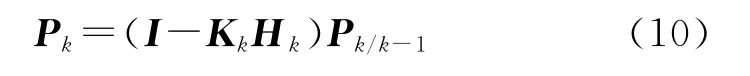
式中：P，Q表示状态方程的误差；R表示量测方程的误差，φ为一步转移矩阵，H为量测矩阵。

状态方程的误差和量测方程的误差在仿真过程中的初值是根据硬件组成及外场测量结果得到的，即将场外实测数据在实验室的处理结果与雷达测量数据进行比较。

滤波初值：

3 仿真结果分析

在卡尔曼滤波动态补偿的仿真过程中，结合旋转稳定弹的改进的质点弹道方程，考虑传感器的零位偏移、安装误差、横轴灵敏度等，得到卡尔曼滤波的量测值，仿真量测量系统如图1所示。

图1 仿真量测量系统

在仿真过程中，弹道系数、射角、初速的初始条件为：c0～N（0.475 0，0.002 6），θ0～N（47，0.682 3）（°），v0～N（850，2.34）（m／s）。

在标准大气模型下某次仿真结果如图2～图7所示。图中，aa为轴向加速度误差，ac为弹丸质心绝对加速度，abc为补偿后轴向加速度，aa，bc为轴向加速度补偿后误差。

图2 转速随时间变化曲线

图3 轴向加速度传感器的实际输出曲线

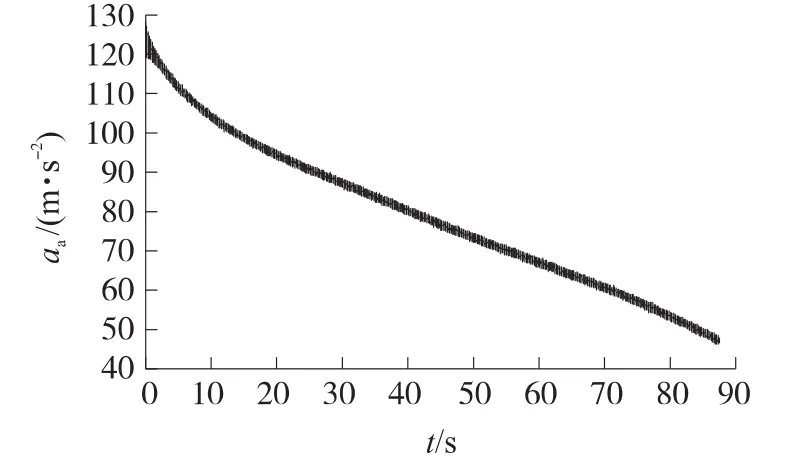
图4 轴向加速度误差曲线

图5 补偿后轴向加速度与弹丸质心绝对加速度曲线

图6 轴向加速度补偿后误差曲线

图7 动态补偿估计出的比例系数曲线

从仿真结果可以看出，补偿后的加速度误差非常小，且全弹道估计出的比例系数近似为一常数。

4 靶场试验结果分析

针对某次靶场试验的加速度传感器测量的数据，用上述的动态补偿算法对试验数据进行补偿。其中每一发产品一前一后安装2个加速度传感器，结合雷达外测数据，得到补偿误差的统计结果，见表1，表中，μa为均值，σa为均方差。其中某一次标定结果如图8和图9所示，图中，a为轴向加速度。

表1 试验数据标定结果统计

图8 靶场试验轴向加速度传感器输出曲线

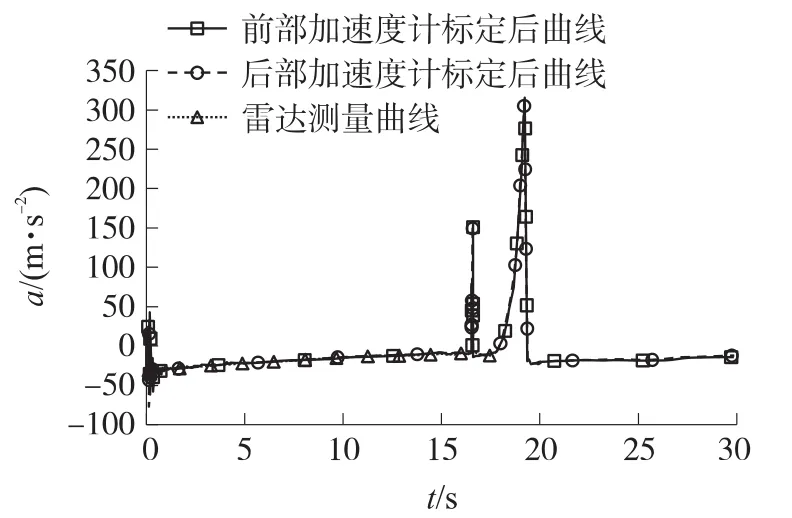
图9 轴向加速度标定曲线与雷达测量曲线

对6个加速度传感器的补偿数据进行统计。

6次补偿误差均方差为0.197 0m／s2，均值为－0.032 9m／s2。6次补偿后均方差为2.012 5m／s2，综合概率误差为2.022 1m／s2。

综上所述，针对同一发产品，由于2个加速度传感器的安装位置不同（安装在弹丸轴线上2个加速计），其测量结果差别非常大，但对传感器的测量值进行补偿后，与雷达测量值比较误差非常小，而且2个传感器补偿后结果也很一致，补偿后的加速度测量误差均值小于0.05g，均方差小于0.32g。实际加速度传感器测量值与雷达测量值的误差补偿前均值为5g左右，而补偿后测量误差均值小于0.05g，轴向加速度测量误差的均值由0.1g降低到0.01g的量级，大幅度地提高了轴向加速度测量精度，在一定程度上说明了补偿算法具有一定的的准确性和有效性。

5 结论

本文通过卡尔曼滤波对弹丸轴向加速度输出误差表达式当中的比例系数C进行估计，从而对加速度传感器的输出值进行补偿，以此得到弹丸的实际轴向加速度。蒙特卡洛模拟仿真和外场试验证实了文中理论分析的正确性和误差减小方法的有效性。

［1］MERHAV S J.A no gyroscopic inertial measurement unit［J］.Journal of Guidance，1982，5（3）：227－235.

［2］殷栩.基于加速度计的炮弹惯性测量硬件系统设计［D］.哈尔滨：哈尔滨工业大学，2006：3－4.YIN Xu.Hardware system design of shells inertial measurement based on accelerometer［D］.Harbin：Harbin Institute of Technology，2006：3－4.（in Chinese）

［3］孙志明.硅加速度计在末制导炮弹测试中的应用［J］.弹箭与制导学报，2003，23（1）：91－93.SUN Zhi－ming.Applications of silicon accelerometer in guided projectile test［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2003，23（1）：91－93.（in Chinese）

［4］FLECK V，SOMMER E.Study of real－time filtering for an inertial measurement unit with magnetometer in a 155mm projectile［C］／／IEEE／ION Position，Location and Navigation Symposium.Coronado，USA：IEEE，2006：83－87.

［5］BROWN T G.Harsh military environments and microelectromechanical devices［C］／／The Second IEEE International Conference on Sensors.Toronto：IEEE，2003：753－760.

［6］杨慧娟.旋转稳定弹轴向加速度测量误差模型分析［J］.弹道学报，2013，25（4）：48－52.YANG Hui－juan.Measnrement error model analysis of axial acceleration for rotational stability bomb［J］.Journal of Ballistics，2013，25（4）：48－52.（in Chinese）

［7］CRASSIDIS J L，MARKLEY F L.Unscented filtering for spacecraft attitude estimation［J］.Journal of Guidance，Control，and Dynamics，2003，26（4）：536－542.

［8］SIMON H.Kalman filtering and neural networks［M］.New York：John Wiley ＆ Sons，Inc，2001：215－218.

［9］LEONARD C.Modified projectile linear theory for rapid trajectory prediction［J］.Journal of Guidance，Control，and Dynamics.2005，28（5）：375－377.