导电纤维丝团空中展开与飘落运动特性
张广华,冯顺山,葛 超,王 超,方国燚
(北京理工大学 爆炸科学与技术国家重点实验室,北京100081)
导电纤维丝团是导电纤维弹中的有效装填物,用于毁伤目标。丝团一般以子母弹的形式装填在母弹当中,根据母弹弹体结构的不同,装填丝团的个数一般为几十个到上百个不等。每个丝团上都缠绕有几十m长的导电丝束,用于搭挂于目标上并引发短路效应。
丝团被抛出后,在运动惯性力、重力及气动阻力的联合作用下,一边向下运动一边展开;展开后的丝束在空中飘移下落一段距离后以一定的概率搭挂于变电站或高压线等供电设施上,通过其短路引弧效应导致目标乃至整个区域内的电力系统瘫痪。
丝团空中展开及飘落的运动规律直接影响到展开后的丝束能否准确地搭落到被攻击的目标之上,并对其进行有效的毁伤,并且可以对导电纤维弹的终端弹道设计(抛丝团高度、速度等)提供依据。目前,国内外关于丝团及导电丝束空中运动规律的研究不多[1-3],因此,本文建立了一种用于描述丝团空中运动的弹道模型,阐述其空中运动特性。
1 丝团运动模型
1.1 假设条件
导电纤维丝团的结构如图1所示。
丝团从母弹中被抛出时的运动姿态及空中运动时受到的风力影响是不确定的,如果考虑所有因素,将会给研究带来较大的困难。因此,为了便于建立空中运动模型,特做如下假设:①丝团被抛出母弹时的运动姿态为水平运动;②丝束展开过程中只考虑丝轴绕丝束的旋转运动而忽略其它运动;③丝轴及丝束受到的风力及风向固定不变,风向为水平方向;④不考虑丝束在展开过程中的弯曲;⑤忽略阻力叶片绕丝束的转动。

图1 导电纤维丝团结构图
1.2 丝团展开模型
以大地坐标系为基准坐标系,丝团展开过程示意图如图2所示。

图2 丝团展开过程示意图
丝束展开长度随时间的变化规律:

式中:l为丝束展开长度为丝束展开速度,R为丝团的半径为丝轴旋转角速度。
丝轴旋转时的角速度及角加速度的变化规律如下:

式中:y为丝轴(丝轴连同未展开的丝束)在竖直方向的运动距离,yc为已展开丝束在竖直方向的运动距离,θ为丝束与y轴间的夹角。
丝团运动过程中,随着丝束的不断展开,缠绕在丝轴上的丝团半径R也在不断变化,R的变化规律为
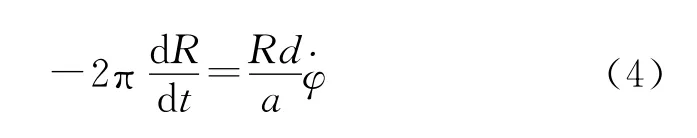
式中:a为丝轴的长度,一般取为1.5~2cm,d为单根丝束的直径,一般取为0.2~0.5mm。
1.3 未展开丝团的运动模型
未展开丝团包括丝轴及缠绕在丝轴上的未展开的丝束,其受力情况如图3所示。

图3 未展开丝团受力图
图3 中,F1x,F1y分别为丝团受到的水平方向和竖直方向的空气阻力;G1,G2分别为丝轴及未展开丝束所受到的重力;FT为已展开丝束对丝团的拉力;Ff1为丝团受到的风动力。根据图3所示未展开丝团的受力情况,建立其运动方程:

式中:x,y分别为丝团在基准坐标系下的水平运动距离和竖直运动距离;J为丝轴旋转时的转动惯量;m为丝轴及未展开丝束的质量和,m=mz-lρl,其中,mz为丝团初始质量,ρl为丝束线密度。
1.4 已展开丝束的运动模型
已展开丝束的受力情况如图4所示。

图4 已展开丝束受力图
图4 中,F2x和F2y分别为已展开丝束受到的水平方向和竖直方向的空气阻力;F3x,F3y分别为阻力叶片受到的水平方向和竖直方向的空气阻力;Ff2和Ff3分别为已展开丝束及阻力叶片受到的风的作用力;G3为已展开丝束受到的重力。A点为已展开丝束与丝轴的交点,C点为已展开丝束的中心点,B点为阻力叶片与丝束的交点。
根据图4所示已展开丝束的受力分析,建立其运动方程:

式中:xc为已展开丝束的水平运动距离;mc为已展开丝束的质量,mc=lρl;J1为已展开丝束绕丝束与丝轴的接触点A转动时的转动惯量。
1.5 丝团展开及飘落运动方程组
联立式(1)~式(10),辅以丝团运动过程中运动距离、速度之间的微分关系式,得到了基于假设条件下的丝团空中展开与飘落外弹道模型:

本文以MATLAB软件为基础,以四阶龙格-库塔算法为求解方法,编制了相应的程序对方程组(11)进行数值求解[4]。结合相关试验(地面抛撒试验、靶场飞行试验)结果及方程组(11)反推出了方程组(11)中的相关气动参数,并根据文献[5-6]提供的方法对丝团及丝束所受气动力进行计算;转动惯量根据文献[7]提供的方法计算。
2 试验研究
为了对本文所建立模型的合理性进行验证,进行了单个丝团的定向抛撒试验及靶场飞行试验。其中,抛撒试验主要用于研究丝团的空中展开规律,靶场飞行试验主要用于研究丝团的空中飘落规律。
2.1 试验丝团的技术状态
试验丝团的技术状态如表1所示,表中,la和lb分别为阻力叶片的长度和宽度,lss为缠绕在丝轴上的丝束长度。

表1 试验丝团的技术状态
2.2 地面抛撒试验
地面抛撒试验的现场布局如图5所示。

图5 地面抛撒试验布局示意图
地面发射装置将丝团发射出去后,通过高速摄像设备记录其空中运动状态;将高速摄像设备拍摄的结果导入到与之配套的后台软件上,并对其进行相应的后处理,即可得到丝团空中展开时的运动参数随时间的变化情况。
2.3 靶场试验
2012年6月28日于某靶场进行了导电纤维丝团空中抛撒的飞行试验。
试验丝团装填于特定的抛撒装置中进行发射;抛撒装置运动到一定高度后将丝团从空中进行抛撒,并通过三坐标跟踪雷达测量得到了丝团空中运动时的各项参数。
3 结果分析
根据抛撒试验及靶场飞行试验的试验条件对方程组(11)中的各个变量赋予如表2所示的初始值。

表2 方程组(11)变量初始值
3.1 丝束展开规律
选取典型时刻的丝束展开长度值为分析对象,将数值计算结果与抛撒试验结果进行对比,对模型进行验证。因为地面抛撒试验的发射装置距离地面较低,试验时丝团在空中运动0.48s后便已着地,所以只能对0.48s之前的相关数据进行对比分析。试验及数值计算的结果如表3所示,表中,le为试验值,ls为计算值,Δl为绝对误差,Δl/le为相对误差。

表3 丝束展开长度随时间变化值
通过表3可以看出,采用方程组(11)求解出的结果与实验值之间的绝对误差在0.03~0.09m之间,相对误差在1.96%~4.66%之间,二者吻合情况较好。
当抛撒速度为38m/s,风力条件为无风时,对方程组(11)进行求解,求解时间设定为20s,得出丝束展开长度l随时间t的变化情况如图6所示。

图6 丝束展开长度-时间关系
通过图6可以看出,运动初期,丝束以接近均匀速度展开,展开速度为4.5~5m/s,运动到4.5s左右时完全展开。
3.2 丝团飘落规律
由于靶场试验时测试雷达距离抛撒装置较远,加之丝团体积很小,想要对丝团空中运动的全过程进行跟踪测试具有比较大的难度,所以只对其空中抛出位置及落地后的位置进行了测量,由此可以确定丝团在给定抛撒高度下的水平飘移距离。试验及数值计算的相关数据如表4所示,表中,yp为抛丝团高度;xe,xs分别为丝团飘移距离试验值和计算值,Δx为绝对误差,Δx/xe为相对误差。

表4 丝团飘移距离
通过表4可以看出,丝团飘移距离的计算值与试验值之间的绝对误差在2.7~5.4m/s之间,相对误差在4.48%~6%之间,二者吻合程度较好。
当抛撒速度为139.9m/s,风力条件为无风时,对方程组(11)进行求解,求解时间设定为20s,得出丝团的飘落规律如图7、图8所示。丝团空中全展后的丝束长度有几十m,其运动状态为丝轴连带着已展开的丝束共同飘落。因此,丝轴的飘落状态可以反映出丝束的飘落状态,为了便于对丝团的飘落规律进行分析,下文中以丝轴的水平及竖直运动距离为研究对象,对其飘落规律进行研究。
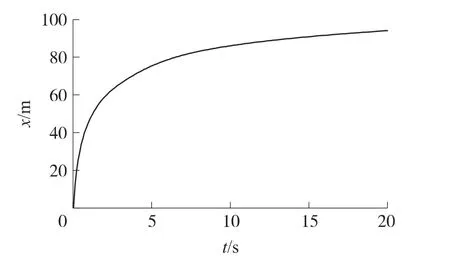
图7 丝轴水平运动距离-时间关系

图8 丝轴竖直运动距离-时间关系
通过图7可以看出,丝轴在水平方向是以减速度状态运动的,这是由空气阻力及已展开丝束对丝轴的拉力作用造成的;运动到10s左右时丝轴的水平运动距离变化越来越缓慢,说明在10s左右时其水平方向的运动速度已经衰减到了接近于0的状态。在20s的时间内,丝轴在水平方向共运动了92.3m。
通过图8可以看出,在运动初期3~4s的时间内,丝轴在竖直方向是以加速状态运动的,这是由其自身重力大于竖直方向的空气阻力所造成的;随着竖直方向运动速度的不断增大,丝轴所受空气阻力也逐渐增大,最后,其自身重力与阻力达到平衡的状态。所以,在4s过后,丝轴以接近匀速的状态下落,下落速度为8.5~9m/s。在20s的时间内,丝轴在竖直方向共下落了195.5m。
根据图7、图8所示内容,绘制丝轴的运动轨迹,如图9所示,图9所示内容与试验时观测到的丝轴运动轨迹吻合。

图9 丝轴空中运动轨迹
4 结论
①通过对导电纤维丝团空中展开与飘落过程中的受力情况进行分析,建立了基于一定假设条件下的丝团空中运动外弹道模型。此模型可以对丝团在不同抛撒条件(风速、抛撒丝团高度、抛撒速度等)下的展开及飘落情况进行预测。
②为了验证模型的合理性,进行了单个丝团的定向抛撒试验及靶场飞行试验,计算结果与试验结果吻合较好,表明本文所建立的丝团弹道模型合理。
[1]COSTELLO M F,FROST G W.Simulation of projectiles connected by a flexible tether,ARL-CR-456[R].2000.
[2]张国伟,冯顺山,孙学清,等.导电丝束空中展开规律[J].弹道学报,2006,18(1):48-50.ZHANG Guo-wei,FENG Shun-shan,SUN Xue-qing,et al.The spreading law of conductive fiber in the air[J].Journal of Ballistics,2006,18(1):48-50.(in Chinese)
[3]刘显江,孙旭,赵非玉,等.美军CBU-94型断电弹药投放落点分析[J].光电技术应用,2007,22(3):21-23.LIU Xian-jiang,SUN Xu,ZHAO Fei-yu,et al.Analysis of the point fall of CBU-94blackout bomb[J].Electro-Optic Technology Application,2007,22(3):21-23.(in Chinese)
[4]张德丰.MATLAB数值计算方法[M].北京:机械工业出版社,2010:225-229.ZHANG De-feng.Numerical computation method of MATLAB[M].Beijing:China Machine Press,2010:225-229.(in Chinese)
[5]浦发.外弹道学[M].北京:国防工业出版社,1980:21-22.PU Fa.External ballistics[M].Beijing:National Defense Industry Press,1980:21-22.(in Chinese)
[6]杨启仁.子母弹飞行动力学[M].北京:国防工业出版社,1999:20-24.YANG Qi-ren.Flight dynamics of cluster bomb[M].Beijing:National Defense Industry Press,1999:20-24.(in Chinese)
[7]梅凤祥,周际平,水小平.工程力学(下册)[M].北京:高等教育出版社,2003:412-416.MEI Feng-xiang,ZHOU Ji-ping,SHUI Xiao-ping.Engineering mechanics(Volume Two)[M].Beijing:High Education Press,2003:412-416.(in Chinese)

