基于遗传算法的复合推进剂粘弹性本构参数研究
郑 健,韩 波,周长省
(南京理工大学 机械工程学院,南京210094)
端羟基聚丁二烯(hydroxyl terminated polybutadiene,HTPB)推进剂是一种常用的复合推进剂,其力学行为十分复杂,其性能依赖于温度和应变率,为了能够准确地描述出该种推进剂装药在受力状态下的力学行为,需要使用粘弹性本构模型。粘弹性本构参数获取的准确性影响仿真分析的准确性,而常规粘弹性实验参数的获取方法均存在较大的实验误差。为了解决这一问题,Zapas-Phillips和Sorvaris等人[1-2]在研究了由试验机加载产生的误差问题之后,分别使用近似积分处理的方法来获取较为准确的松弛模量数据。Zapas-Phillips法使用积分中值定理来获得修正的松弛模量数据,但是仅能得到t≥t1/2时刻的松弛模量数据,其中,t为松弛时间,t1为达到恒应变的时间。Sorvaris法在此基础上进一步研究、推导出了t≥0时刻的松弛模量数据。孟红磊等人[3]在Sorvari方法的基础上提出了改进型的Sorvari方法,即引入修正因子α来更加精确地近似积分过程。许进升等人[4]基于直接积分方法来获取复合HTPB推进剂的松弛模量数据。
本文提出了一种基于遗传算法的HTPB复合推进剂粘弹性本构参数获取方法,为固体火箭发动机装药结构完整性分析提供准确的本构参数。
1 本构参数获取
1.1 问题描述
HTPB推进剂是一种典型的粘弹性材料,其力学特性呈现出弹性固体和粘性流体的性质,在固体火箭发动机装药完整性分析中常使用线粘弹性本构模型来表征推进剂的力学行为。三维积分型的各向同性线粘弹性材料应力-应变关系可以表示为
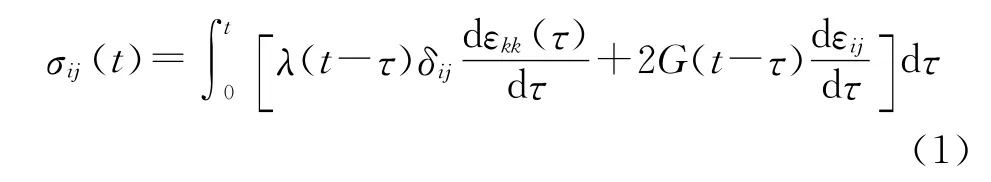
应力-应变关系的应力偏量部分sij和体变部分σkk分别为
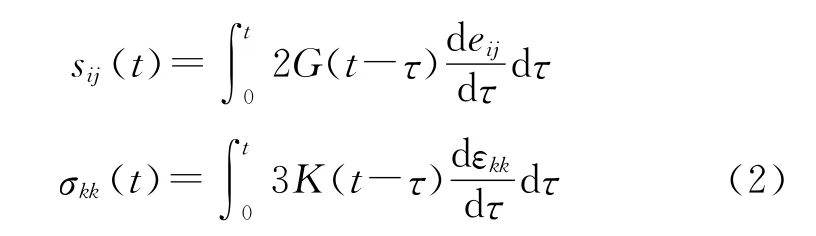
式中:λ(t),G(t),K(t)分别为拉梅常数对应的松弛函数、剪切松弛函数和体积松弛函数;δij为位移分量,eij为偏应变张量,εkk为应变偏量。对于各向同性线粘弹性材料,必须具备2种材料函数才能准确描述其应力-应变特性。但是通过实验直接获得粘弹性材料的材料函数G(t)和K(t)比较困难,而材料的松弛模量E(t)较容易获得。因此,如果获得了材料函数之间的转化关系,就可以通过较容易测量的材料函数来表征线粘弹性材料的力学行为。
将式(2)进行Laplace变换,得到:
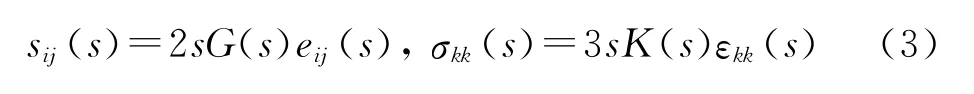
式中:s为Laplace变换的复变量。弹性力学中材料常数存在以下关系:
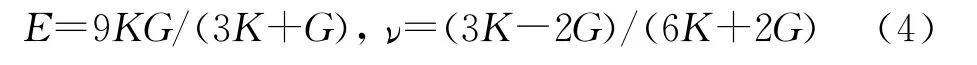
式中:E为松弛模量,ν为泊松比。
将式(4)中的参数进行Laplace变换,得到:
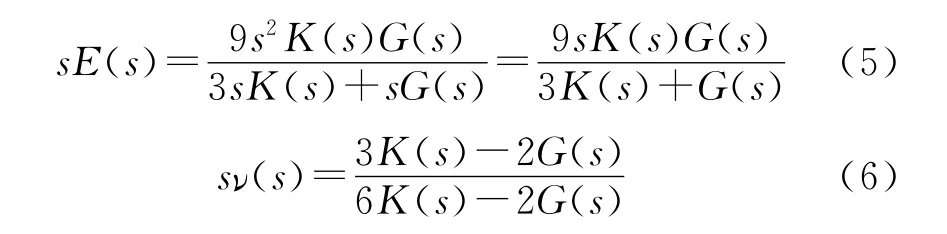
对式(5)、式(6)进行Laplace逆变换可以得到线粘弹性材料中E(t),ν(t)和G(t),K(t)之间的关系。实际工程应用中,可以根据实际情况简化材料函数之间的变化关系。在固体推进剂有限元计算中经常采用下列假设:由于泊松比ν(t)随时间变化很小,故假设泊松比为常数,则根据松弛模量E(t)可以得到剪切松弛模量G(t)和体积松弛模量K(t):
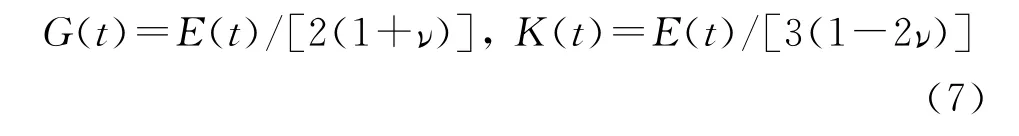
因此,如何准确地获得推进剂的松弛模量对结构完整性分析十分重要。
1.2 传统实验方法
现行的复合推进剂松弛模量测定方法是使用拉伸试验机快速地将推进剂试样拉至某一恒定应变,同时测量出推进剂的松弛应力,从而拟合出该推进剂材料的静态松弛模量[1-2]。
图1给出了阶跃位移和加载示意图。
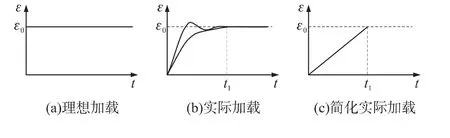
图1 阶跃位移加载示意图
图1 (a)表示试验机系统的理想加载过程,即不考虑加载历程。但真实情况下试验机通过调节控制系统的PID参数,实际的上升阶段可能存在超调、缓慢爬坡等现象,即存在加载历程,如图1(b)所示。且HTPB推进剂的松弛响应较快,因此采用图1(a)这种数据处理方法会造成实验获得的静态松弛模量数据偏小。为了解决这一问题,很多研究学者提出了各种数据处理方法,但这些方法均假设试验机的加载阶段近似为一个直线上升的阶段,即如图1(c)中所示的加载历程。国外Zapas-Phillips采用积分中值定理获得修正的t≥t1/2时刻的松弛模量数据,其计算式如下:
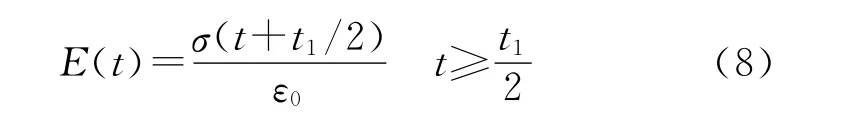
Sorvaris[1-2]在 Zapas-Phillips的研究基础上,推导出了t≥0时刻的松弛模量数据表达式:
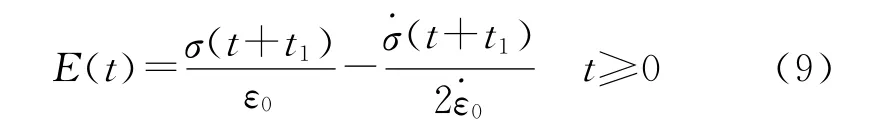
式中 :σ为应力为应力变化率 ,ε为应变为应变变化率。
国内孟红磊[3]在Sorvari方法的基础上提出了改进型的Sorvari方法,即引入修正因子α来更加精确地近似积分过程:
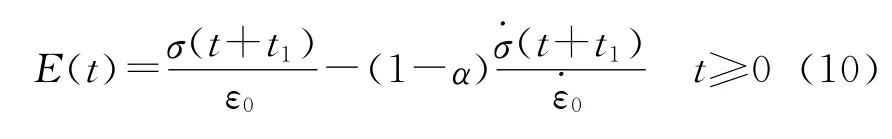
许进升等人[4]基于直接积分方法来获取复合HTPB推进剂的松弛模量数据,即通过理论推导出Prony级数形式的松弛函数在图1(c)加载条件下松弛应力的显式表达式,再通过最小二乘法来获得静态松弛模量。
虽然这些方法在一定程度上提高了实验数据的准确性,但是与实验过程中真实的加载过程仍存在一定的差异。
1.3 基于遗传算法的松弛模量获取
使用基于遗传算法的全阶段松弛模量数据拟合方法解决实验系统和数据处理带来的松弛数据不准确问题。遗传算法(genetic algorithm,GA)是由美国Michgan大学的Holland J教授于1975年最早提出,它是一种借鉴了生物学进化规律的算法,该算法模拟了生物学的遗传、突变、自然选择和杂交等现象。对于一个优化问题,首先从解空间中随机抽取一定数量的候选解形成一个初始种群,使用一种编码方法对初始种群进行编码。上一代种群内部通过遗传、变异、杂交等过程形成新一代种群,通过算法的适应度函数来判断新种群的优劣,通过这一过程来模拟自然界的优胜劣汰。经过若干代的优胜劣汰获得最优的种群,即最优解。
遗传算法的基本步骤如下:
①编码。使用某种编码方式将解空间映射到遗传算法的编码空间中。
②产生初始种群。在编码空间中随机产生一定数量的码形成初始种群,这些初始种群对应着一组初始解。
③适应度评估。使用适应度函数来判断种群中个体的优劣。
④遗传算子的确定。遗传算子中确定了选择、交叉、变异的整个过程。
⑤算法的终止条件。确定遗传算法的终止条件。
使用MATLAB编制了拟合HTPB推进剂松弛曲线的计算程序,以拟合函数和实验曲线的重合度作为遗传算法中的目标函数,目标函数的表达式为
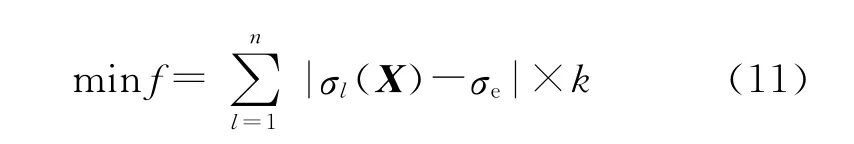
式中:f为适应度,n为计算过程中的迭代次数,即种群繁衍的代数;σl(X)代表优化过程中解空间内某一个体在给定载荷作用下得到的应力值;σe为实验获得的应力值。使目标函数表达式获得最小值的X即为最优解,即为所需要的松弛模量拟合参数。为避免目标函数在寻优过程中数值过小影响计算精度,将式(11)乘以一个较大的系数k可以将目标函数适当放大(此处k取10 000)。
2 实验方法和结果处理
为了获得准确的推进剂松弛模量数据,使用美国BOSS动态力学实验机进行实验,该实验机具有加载速度快、采集系统精度高等特点。为了能够满足动态力学实验机的材料安装要求,参照文献[5]中的单轴拉伸实验方法设计了单轴应力松弛试样。
图2为松弛实验的试样示意图。使用刀片将HTPB推进剂切割成长条形试样,试样尺寸B=5mm,W=5mm,H=30mm。使用改性丙烯酸胶粘剂将HTPB推进剂试样上下两端和木质接头粘接,试样制作完成后放入密封干燥箱中在室温下静置24h进行固化。实验设备如图3所示,整个实验系统由控制柜、动态力学分析仪DMA、保温箱、液氮罐和非接触式应变测量系统组成。HTPB推进剂模量较低且容易造成损伤,不宜直接使用引伸计来测量拉伸应变。直接使用实验机的加载位移来反推试样应变存在较大的误差,因此实验中采用基于数字图像相关性的非接触式应变测量系统来测量拉伸过程中推进剂的应变。
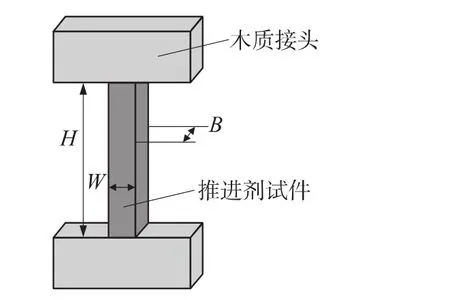
图2 松弛试样示意图

图3 DMA实验系统
以松弛实验过程中的实际位移变化曲线作为输入条件开始遗传算法的计算,图4给出了优化计算过程中的优化历程,图中,n为计算过程中种群繁衍的代数,f为种群在优化过程中的适应度。图中给出了适应度的最优值和平均值。从图中可以看出,在种群的繁衍过程中种群的适应度不断下降,这表明种群的质量在逐步提高,经过292代之后种群的最佳适应度之间达到一个稳定值,并认为第292代中的最优个体即为最优解。计算结果如表1所示。表中,E0=8MPa(瞬态松弛模量),N为Prony级数的阶数,EN,tN分别为各阶松弛模量、松弛时间。
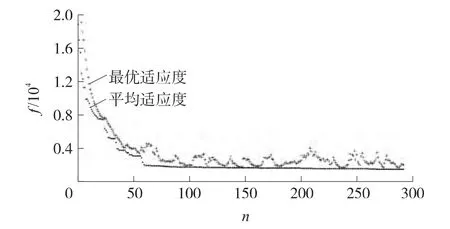
图4 遗传算法计算过程中适应度最优值和平均值变化情况
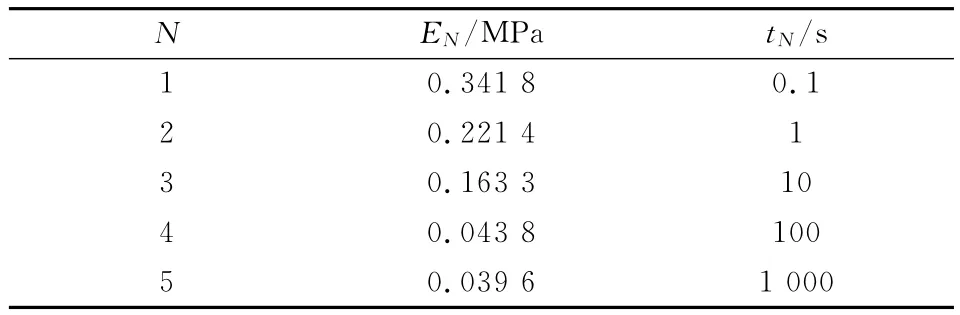
表1 松弛实验数据
分别使用传统计算方法和遗传算法获得了HTPB推进剂的松弛模量数据,将该结果应用于真实松弛实验的加载过程中,所得的应力σ随时间变化结果如图5所示。从图中可以看出,遗传算法结果和实验结果吻合良好,而传统方法所得到的结果明显小于实验结果;随着时间的增加,传统方法和遗传算法的差距逐渐减小。由于传统方法忽略了实验过程中加载阶段对实验结果的影响,因此其获得的结果偏低。但是加载阶段对于HTPB推进剂的平衡模量的影响随着时间逐渐减小,因此传统方法和遗传算法的差距会随着时间的推移逐渐减小,直至重合。
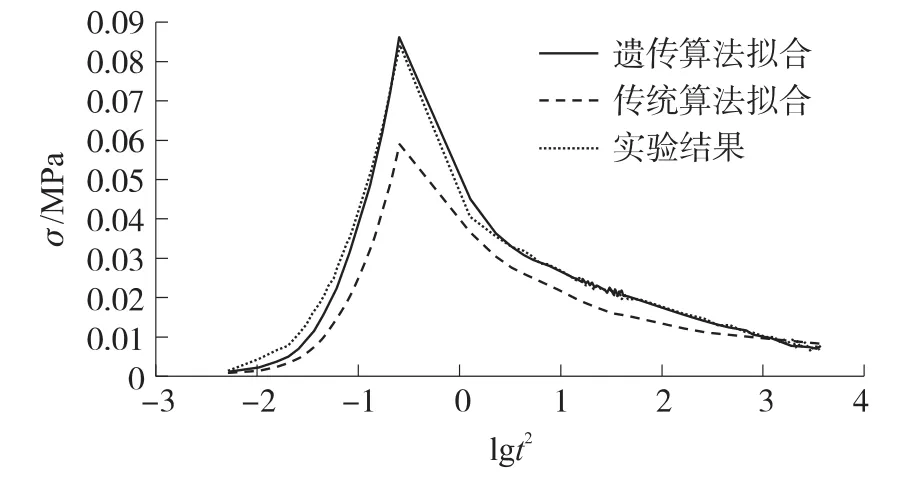
图5 遗传算法和传统算法结果对比
3 结论
本文建立了基于遗传算法的复合推进剂松弛模量获取方法,为该推进剂的粘弹性本构模型提供了较精确的本构参数,获得如下结论:①由于拉伸试验机系统存在加载历程,传统松弛模量获取方法获取的数据较真实值偏小;②基于遗传算法的松弛模量拟合方法考虑了真实实验过程中的加载历程,因此可以准确地获得复合推进剂的松弛模量。
[1]SORVARI J,MALINEN M.On the direct estimation of creep and relaxation functions[J].Mechanics of Time-dependent Materials,2007(11):143-157.
[2]SORVARI J,MALINEN M.Numerical interconversion between linear viscoelastic material function with regularization[J].Solids and Structures,2007,44:1 291-1 303.
[3]孟红磊.改性双基推进剂装药结构完整性数值仿真方法研究[D].南京:南京理工大学,2011.MENG Hong-lei.Research on numerical simulation method of structure integrity analysis for modified double base propellant grain[D].Nanjing:Nanjing University of Science and Technology,2011.(in Chinese)
[4]许进升,鞠玉涛,郑健.复合固体推进剂松弛模量的获取方法[J].火炸药学报,2011,34(5):58-62.XU Jin-sheng,JU Yu-tao,ZHENG Jian.Acquisition of the relaxation modulus of composite propellant[J].Chinese Journal of Explosive & Propellants,2011,34(5):58-62.(in Chinese)[5]JUNG G D,YOUN S K.A nonlinear viscoelastic constitutive model of solid propellant[J].International Journal of Solids and Structures,1999,36(25):3 755-3 777.

