分布式高炮火控系统空域窗射击方法

刘 恒，梅 卫，单甘霖

（军械工程学院 电子与光学工程系，石家庄050003）

高炮系统在低空近程防空反导中有着不可替代的作用［1］。传统上，高炮普遍采用集火射击方式拦截空中目标。随着空中目标机动性能的不断提高，火控系统的运动假定难以与其实际航迹精确吻合，这使得提前点的预测精度下降。为克服集火射击的缺点，20世纪80年代国外提出了一种新型火控方法——未来空域窗射击体制［2］，即在预测未来点的近旁建立弹丸或破片具有近似均匀散布特性的未来空中区域。当目标发生有限机动时，使其尽可能覆盖目标。可能因该技术尚不成熟，国外关于该技术的文献资料非常少。从20世纪90年代开始，国内南京理工大学等高等院所［3－5］也开展了相关的研究，取得了一些成果。与此同时，传统的功能集中的火控体制结构因受多种因素的影响已不能适应新的作战要求，而采用数字化节点的分布式火控体系结构得到广泛的研究和应用［6－8］。分布式火控系统是指整个系统在体系结构上实现地点上的分布、功能上的分布及控制上的分布。采用分布式体系可以提高火控系统的应变能力，使其在复杂战场环境下的生存能力和威力得以提高。可以预见，采用空域窗射击方式的分布式高炮系统定会在增大自身生存概率的同时，提高空中目标的拦截概率。

本文研究在高炮分布式配置条件下如何实现空域窗射击，解决其射击诸元解的存在性问题。

1 分布式高炮系统及空域窗射击原理

分布式火控系统的结构如图1所示，它包括1辆指挥车（记为高炮火控中心计算机）和3个实现了信息共享的子系统，每个子系统由1部火控单元和2门火力单元（高炮）组成。各子系统火控单元接收火控中心计算机转发的目标现在点坐标、射击控制指令等，自行解算下属各火力单元的射击诸元（包括射角、提前方位角和弹丸飞行时间）。关于分布式火控系统之间的信息传输、时间同步等问题可参阅文献［7］。

图1 分布式火控系统结构示意图

图2 是空域窗射击方式下窗内弹丸散布中心配置示意图（以圆形空域窗内6个弹丸散布中心为例）。其中，点O是目标预测未来点，按照传统火控系统解命中计算得到。点1～6是空域窗内弹丸散布中心，r为空域窗半径。第i个散布中心与O点的相对位置偏差量Xi（i＝1，2，…，6）为

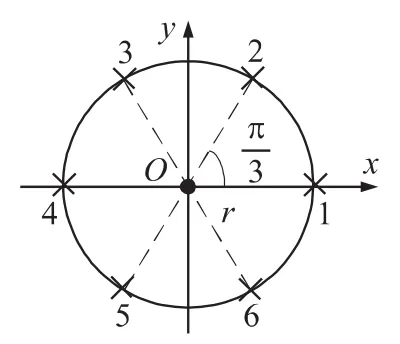
图2 未来空域窗射击弹丸散布中心配置

实现空域窗射击的约束条件：

①时间约束，弹丸同一时刻抵达各自散布中心；

②空间约束，弹丸散布中心以预测未来点为圆心呈规律性分布。

2 时空域射击窗

定义1 弹丸按照所属火力单元赋予的射击诸元，经过各自弹丸飞行时间的飞行后，于同一时刻抵达空域窗内的各预定散布中心，实现对目标同一未来点的火力包围，即在时间域和空间域上均满足空域窗约束条件，称之为时空域射击窗。其射击示意图如图3所示（以3门高炮为例）。假设共有m门高炮，与各弹丸散布中心一一对应，则时空域射击窗的流程如图4所示。其中，虚线框图1是各子系统火控机（记为高炮火控机）一次处理过程，虚线框图2是各子系统火控机二次处理过程。

与集中配置的高炮系统相比，受其空间基线的影响，各火力单元的射击诸元相差较大，尤其是射弹飞行时间大小不一致，这产生了各火力单元射击时机的协调配合问题，即分布式各火力单元弹丸飞行时间可行解是否存在的问题。在提出解决问题的方法前，先简单介绍空域窗射击方式的概念和基本原理。采用未来空域窗射击方式时，通过对射击诸元的指向点作适度的分离，可造就一个同目标预测误差分布区相重、具有近似均匀分布且具有足够毁伤能力的射弹分布区域。

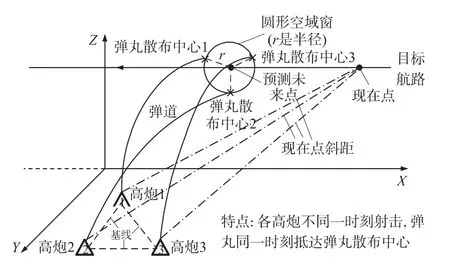
图3 分布式火控系统时空域射击示意图

图4 火控算法流程图

具体实现步骤：

①高炮火控中心计算机将当前时刻t0的目标现在点，基于目标运动假定沿时间轴外推至未来某时刻tp，然后通过基线修正，得到tp时刻各高炮目标现在点坐标。Δt＝tp－t0是完成协同需要的时间，包括高炮火控中心计算机和各高炮火控单元之间完成通信、解算，高炮随动系统完成随动等所需时间，其大小可通过离线统计分析计算［6］。

②（子系统火控机一次处理）各高炮对tp时刻的现在点解相遇得到各自的弹丸飞行时间tf，i（i＝1，2，…，m）后，高炮火控中心计算机对tf，i（i＝1，2，…，m）进行比较，选取最长弹丸飞行时间tf，max＝max｛tf，i，i＝1，2，…，m｝，并将tp＋tf，max设定为弹丸抵达各散布中心的同一时刻。

③高炮火控中心计算机将当前时刻t0的目标现在点外推至tp＋tf，max时刻，得到目标未来点Dq，然后基于未来空域窗射击原理，计算各高炮弹丸散布中心Dq，i（i＝1，2，…，m）与Dq相对位置偏差量Xi，进而求得其弹丸散布中心Dq，i（又称预设提前点）。

④（子系统火控机二次处理）各高炮根据t0时刻现在点及预设提前点，逆解出飞行时间tf，i与射击诸元方位角和射角（βqq，i，φi）。利用公式ti＝tp＋tf，max－tf，i计算出各高炮的射击时刻。当ti时刻来临时，与之对应的高炮实施射击，弹丸将在飞行tf，i后，于tp＋tf，max时刻抵达其弹丸散布中心。

⑤因为Δt经离线统计得到，对某一次射击诸元解算过程而言，若Δt取值偏小，则不能排除小概率事件t0＞ti（∀i＝1，2，…，m）发生的可能性。若此小概率事件发生，则返回到步骤①，增大Δt值，重新计算；否则，驱动高炮随动系统，等待射击时刻实施射击。

命题 各高炮若按步骤①～步骤⑤给出的射击算法依次实施射击，其弹丸可于同一时刻抵达空域窗内各弹丸散布中心，对目标形成空域窗射击。

证明 为简便并不失一般性，此处以2门高炮为例进行说明。

假设高炮1和高炮2的弹丸飞行时间分别为tf，1和tf，2，并有tf，1＞tf，2。

根据公式tj＋tf，j＝tp＋tf，max（j＝1，2）计算可得，高炮1和高炮2的射击时刻分别为t1＝tp＋tf，max－tf，1和t2＝tp＋tf，max－tf，2。因为tf，1＞tf，2，则有t1＜t2，即高炮1在t1时刻实施射击，高炮2晚于高炮1，在t2时刻实施射击。但2门高炮发射的弹丸将同时于tp＋tf，max时刻抵达各自的弹丸散布中心，满足时间约束；由目标航迹的时空唯一性可知，目标也于tp＋tf，max时刻到达其预测未来点。由于2个弹丸散布中心的位置是根据tp＋tf，max时刻目标预测未来点位置，基于空域窗射击原理得到的，故在目标到达预测未来点的同时，弹丸也将抵达以此未来点为圆心构成的空域窗内，满足空间约束，即高炮系统实现了空域窗射击。

经过以上分析可知，时空域射击窗的本质是通过牺牲射击时机，保证弹丸的同一时刻抵达，以实现空域窗的合成，提高拦截目标的概率，其可与拦阻射击体制结合使用。

3 空间域射击窗

定义2 同一时刻发射的弹丸按照所属火力单元赋予的射击诸元（基于空域窗射击原理计算），经过各自弹丸飞行时间的飞行后，抵达预定的散布中心点，称之为空间域射击窗。因为弹丸飞行时间大小不一致，同一时刻发射的弹丸将不会同时抵达各散布中心，故空间域射击窗方式仅在空间域上满足空域窗的约束条件，在时间约束上并不成立。具体实现步骤：

①高炮火控中心机基于当前时刻t0的目标现在点观测数据解相遇，得到目标预测未来点和弹丸飞行时间t′f。假设空域窗半径为r（t′f），由式（1）计算出各弹丸散布中心与预测未来点的相对位置偏差量Xi（t′f）。

②将Xi（t′f）作为对各门高炮预测未来点的修正量X′i，叠加到解相遇方程组中。

③各高炮火控机根据阵地配置情况，计算t0时刻各自的目标现在点坐标Di，并解相遇求得提前点Dq，i及射击诸元：

式中：tf，i为弹丸飞行时间，si为目标运动的提前量。

④计算出射击诸元后，各高炮即可实施射击。

⑤射击结束的高炮可立即转入下次射击准备过程中。

记τi＝tf，i－t′f表示两者的时间差，Xi（tf，i）表示与第i门高炮相对应的预测未来点修正量。在式（2）中，很显然X′i和Di与tf，i无关，但此处的X′i可记作Xi（tf，i），即Xi（tf，i）＝X′i。又根据前述实现步骤①，②可知，X′i＝Xi（t′f），则有：

成立。

式（3）表明空间域射击窗的空间约束与时间域无关，两者相互独立。

对空间域射击窗方式，给出如下数学解释。借鉴随机过程中平稳过程的思想，空域窗内的各弹丸散布中心的统计特性不随时间变化而变化。其仅与空域窗的半径有关，而与弹丸飞行时间无关，此处的统计特性是指空域窗内各弹丸散布中心与预测未来点的相对位置偏差量。其射击示意图如图5所示（以3门高炮为例）。

图5 分布式火控系统空间域射击示意图

从以上分析可知，空间域射击窗与传统的集火射击区别在于：将空域窗内各弹丸散布中心与预测未来点的相对位置偏差量作为修正量，叠加到解相遇方程组中。与时空域射击窗方式相比，空间域射击窗无需满足时间约束条件，增加了射击时机，可以实现对目标的跟踪射击。

4 仿真验证

1）对空间域射击窗数学解释的仿真验证。

仿真条件：假设在大地直角坐标系下，目标当前时刻现在点（2 000，800，500）（m），圆形空域窗半径r＝20m。目标作水平匀速直线运动，临近飞行，速度（－200，0，0）（m／s），高炮阵地配置如图6所示，图中，Z点是炮阵地中心，各子系统成边长为600m的正三角形配置，子系统内两炮呈一字线性排列，距离200m，共6门高炮。

图6 高炮配置阵地

分别计算出各高炮的弹丸散布中心点及与之对应的目标预测未来点，将其位置坐标值作差得到两者的差值（包括X轴和Y轴方向分量，分别记为d1和d2），分析各差值变化规律，即剔除时间因素后，分析各弹丸散布中心和与之对应预测未来点相对偏差量的分布规律。仿真结果见表1和图7，tf为弹丸飞行时间。

表1 仿真数据

图7中实线表示剔除时间因素后的各高炮d1和d2值，虚线是其最佳拟合曲线（圆形，半径为20.2m）。

分析图7可知，剔除时间因素后，弹丸散布中心近似均匀分布在同一个圆周上，这说明此种方法可以实现空域窗射击，是可行、有效的。

2）3种射击方式毁歼概率仿真。

图7 仿真结果

设置不同的仿真参数，通过蒙特卡罗法计算时空域射击窗、空间域射击窗和集火射击3种方式的毁歼概率，进行分析比较。

仿真条件：目标位置预测误差均方差σ、圆形空域窗半径r和每门高炮发射弹丸数n，分5组见表2；空域窗射击时弹丸散布误差均方差大小是空域窗半径大小的／2，单位m；集火射击时弹丸散布误差均方差为2m；高炮门数6门，毁歼目标所需的平均命中弹数w＝3，目标等效圆半径为5.6m，蒙特卡罗仿真次数为1 000次。

首先判断目标与弹丸是否发生碰撞，检测方法为：计算目标与弹丸的相对距离，若此距离小于目标等效圆半径，则认为弹丸命中目标。统计出所有命中的弹丸数记为N，则一次毁歼概率P计算公式为［3］仿真1 000次，然后对所有毁歼概率P取平均，即为毁歼概率值Pk。

仿真结果如表2和图8所示。

表2 3种射击方式的毁歼概率

图8（a）是在目标位置预测误差均方差为20m、圆形空域窗半径为20m时，3种射击方式的毁歼概率随弹丸数的变化规律曲线；图8（b）是在目标位置预测误差均方差为10m、每门高炮发射5发弹丸时，3种射击方式的毁歼概率随空域窗半径的变化规律曲线。

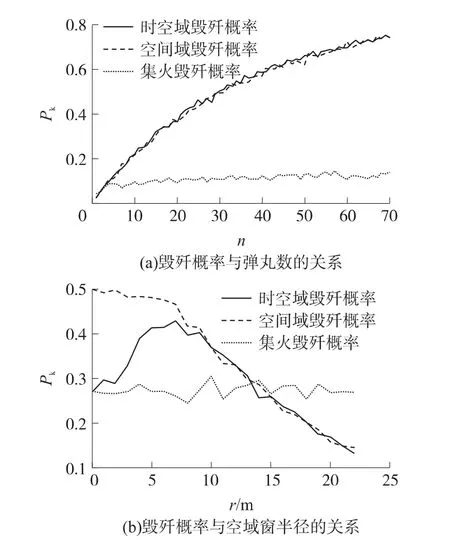
图8 仿真结果

结果分析：

①图8中的6条曲线不严格平滑是由蒙特卡罗仿真次数不够多导致的。但因为各曲线的随机波动均较小，故其对仿真结果的影响可以忽略不计。

②对比表2中第1组、第2组仿真结果及图8（a）可知，在目标位置预测误差较大时，2种空域窗射击方式的毁歼概率相差无几，均优于集火射击。其原因是：2种空域窗射击方式根据目标位置预测误差选择了合适的射击窗半径，扩大了对目标的有效拦截区域，故提高了毁歼概率。随着弹丸数的增加，集火射击毁歼概率提高的幅度有限，虽然2种空域窗射击方式也会出现毁歼概率高原现象，但其毁歼优势却更加明显。原因是：虽然增加了弹丸数，但集火射击的有效拦截区域并未增加，仅仅是在原拦截区域内的弹丸散布密度增大，这就造成了弹丸的浪费。而2种空域窗射击方式将浪费的弹丸配置到弹丸散布密度稀疏的区域，扩大了有效拦截区域，这也是空域窗射击的基本原理。

③分析表2中第3组、第4组仿真结果，在目标位置预测误差较小时，若每门高炮发射的弹丸数偏少，由于空域窗半径选择得过大，导致时空域和空间域射击窗内弹丸散布稀疏，降低了毁歼概率。而集火射击能够集中较少的弹丸数，与前者相比提高了弹丸散布密度，故其毁歼概率大于前者；但当弹丸数增加到20发，增大了射击窗内弹丸散布密度，使其毁歼概率提高幅度大于集火射击提高幅度，导致2种射击窗方式优于集火射击。这说明在弹丸充足的条件下，2种射击窗方式更适用。

④对比表2中第3组、第5组仿真结果及分析图8（b）可知，在其它条件一定的前提下，空域窗半径与目标位置预测误差存在最优匹配关系，使毁歼目标的概率最大。但在同等条件下，2种射击方式最优的空域窗半径及与之对应的毁歼概率最大值不一致；当空域窗半径取为0时，时空域射击方式毁歼概率为0.270 4，空间域射击方式为0.497 6，集火射击方式为0.271 9。此时，时空域射击方式等效为集火射击方式，故两者毁歼概率一致，细微差别是由蒙特卡罗仿真次数不够多引起的。但两者比空间域射击方式效果要差，这是由于后者部分目标预测提前点斜距离小造成的；同时可以看出，当空域窗半径大于8m时，2种射击方式的毁歼效果相差无几，这也解释了图8（a）中2种射击窗方式毁歼概率的变化规律；另外，若空域窗半径取值偏大（大于15m），则会使其毁歼概率比集火射击的还小，这是因为空域窗半径偏大使其内部弹丸散布稀疏，减小了毁歼概率。

综上所述，在本文设置的不同仿真条件下，时空域和空间域射击方式毁歼目标的概率与理论分析结果一致，是可行和有效的。

5 结论

针对高炮分布式配置条件下空域窗射击的实现问题，本文提出了时空域射击窗和空间域射击窗2种射击方式，实现了分布式高炮之间的协同射击。时空域射击窗方式通过牺牲射击时机，保证了弹丸于同一时刻抵达空域窗内各弹丸散布中心，实现了射击窗的合成，提高了拦截目标的概率，其可与拦阻射击体制结合使用；空间域射击窗计算出射击诸元后即可实施射击，不会浪费射击时机，其可与跟踪射击体制结合使用。这2种射击方式对分布式高炮系统空域窗射击方式的工程设计具有一定的参考价值。

［1］薄煜明，郭治，杜国平，等.高炮与防空导弹在近程防空反导中的互补性［J］.兵工学报，2002，23（2）：164－166.BO Yu－ming，GUO Zhi，DU Guo－ping，et al.Complementation of archibald and antiaircraft missile in low range air and antimissile defence［J］.Acta Armamentarii，2002，23（2）：164－166.（in Chinese）

［2］胡金春.未来空域窗体制下的火力控制理论［D］.南京：南京理工大学，1998.HU Jin－chun.Design theory of fire system under future airspace windows system［D］.Nanjing：Nanjing University of Science ＆ Technology，1998.（in Chinese）

［3］胡金春，郭治.未来空域窗的数学描述［J］.兵工学报，1998，19（4）：293－297.HU Jin－chun，GUO Zhi.Mathematical description of future airspace window［J］.Acta Armamentarii，1998，19（4）：293－297.（in Chinese）

［4］刘恒，梅卫，卢大庆，等.自适应射击窗火力控制技术［J］.火力与指挥控制，2012，37（10）：70－73.LIU Heng，MEI Wei，LU Da－qing，et al.Fire control technology featured on adaptive shooting window［J］.Fire Control ＆Command Control，2012，37（10）：70－73.（in Chinese）

［5］孙世岩，邱志明，王航宇，等.拦阻面弹丸散布中心配置方法［J］.弹道学报，2008，20（4）：16－19.SUN Shi－yan，QIU Zhi－ming，WANG Hang－yu，et al.Dispersion center configuraion method of barrage firing curtain［J］.Journal of Ballistics，2008，20（4）：16－19.（in Chinese）

［6］王中许，陈黎.分布式高炮火控系统3种射击方式的实现［J］.兵工学报，2011，32（7）：795－800.WANG Zhong－xu，CHEN Li.Implementation of three shooting modes for distributed fire control system of antiaircraft gun［J］.Acta Armamentarii，2011，32（7）：795－800.（in Chinese）

［7］王中许，张学彪，盛安冬.基于分布式节点的火控体系研究［J］.兵工学报，2005，26（5）：638－641.WANG Zhong－xu，ZHANG Xue－biao，SHENG An－dong.Research on fire control system based on distributed nodes［J］.Acta Armamentarii，2005，26（5）：638－641.（in Chinese）

［8］刘锐，陈枫，盛安冬.基于联邦架构的分布式火控系统拦阻射击方法［J］.火力与指挥控制，2010，35（4）：17－20.LIU Rui，CHEN Feng，SHENG An－dong.A method of barrage fire based on federated distributed antiaircraft system［J］.Fire Control ＆ Command Control，2010，35（4）：17－ 20.（in Chinese）