基于MATLAB的灰色拓扑在交通事故预测中的应用

林登科，陈伯辉，沈斐敏

（福州大学环境与资源学院，福建 福州350108）

0 引言

随着我国经济的高速发展，道路运输在综合运输体系中发挥着越来越重要的作用。在道路交通给人们的生活、经济以及社会带来便利的同时，交通事故的频繁发生也给人民生命财产造成了极大的损失，交通事故已经成为当今社会的一大公害。据统计，2011 年，我国共接报道交通事故422.4万起，比2011年增加了31.8万起，同时每一起交通事故的伤亡人数在不断增加，死亡人数占全年各类生产安全事故死亡人数的比例高达82%，交通事故的死亡率远高于一些发达国家。科学准确地预测交通事故对交通安全的管理工作具有重大的意义。

交通事故具有随机性的特点，但从整体来看，在特定的地区较长时间范围内，交通事故的发生又具有一定的规律性。目前，国内外对交通事故预测进行了很多研究，提出了较多的交通事故预测方法，如回归分析、人工神经网络预测法、灰色理论等[1-5]。本文提出了一种基于灰色拓扑的交通事故预测，灰色系统分析方法对于信息不完整或不完全的实际情况具有良好的适用性。灰色拓扑正是基于灰色理论发展起来的，GM（1，1）模型的主要优点是它能反映事物发展的变化趋势，然而由于它的形状简单，属于特定的指数曲线，当原始数据的变化较大，波形的起伏较大的时候，这种模型就不能很好地做出预测。灰色拓扑正是弥补了这个不足，它的实质是对原始数据的变化波形进行预测，所以当数据较多且波形变化较大时，利用灰色拓扑进行预测具有一定的可行性[6]。

本文根据福建省统计局网站《福建统计年鉴》中2005—2013 年各月份福建省交通事故死亡人数数据，利用灰色拓扑建立中长期的预测模型，将系统的阈值分层次地利用灰色预测模型进行预测，再将各分层的预测结果放在同一预测面上，形成预测波形，对各预测值通过理论的检验判断模型的有效性。

1 灰色拓扑的原理

灰色拓扑预测又称图形预测，是根据系统特征值分层次对原始数据的波形进行预测。将原始数据绘制成曲线，选取一组合理的阈值，在曲线上按照给定的阈值找到相应的时刻，用这些时刻的数据分别建立GM（1，1）模型，再用这些模型预测这些阈值将来出现的时刻，最后将这些预测值连成曲线，得到预测曲线，称为拓扑预测。灰色拓扑预测的具体步骤如下[7]：

（1）根据原始数据x（0）（k），以时间为横坐标轴，原始数据为纵坐标轴，利用MATLAB 绘制发展曲线；

（2）取阈值ci（i=1，2，3，…，n），且Minx（0）≤ci≤Maxx（0）；

（3）在原曲线上作高度为ci的水平线，得到交点横坐标数列

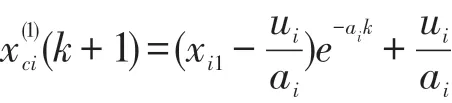
（5）检验模型的精确度，模型精确度标准见表1；

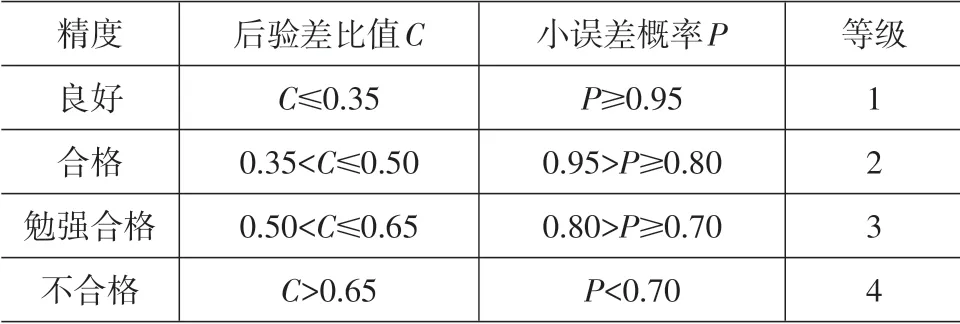
表1 精度检验等级

（6）利用模型预测各阈值将来时间的时间点。

2 灰色模型的MATLAB实现

在灰色拓扑预测中，需要用到多组的GM（1，1）模型预测，而在GM（1，1）模型预测中，要涉及到较多的数列及矩阵的计算，其计算过程较为复杂。MATLAB 是以线性代数软件包LINPACK 和特征值计算软件包EISPACK 中的子程序为基础发展起来的一种开放性程序设计语言，可以直接对各种矩阵进行计算。在交通事故死亡人数预测中引入MATLAB 编程可以实现灰色预测，大大减少了计算量以及提高计算的准确度，改善预测的质量[8-10]。

程序中涉及到的参数有：

Sr为原始数列；X1为累加数列；Z1为邻均值累加数列；B、Yn为微分方程系数矩阵；a为发展系数；b为灰作用量；sc1为预测的累加数列；sc0为预测值数列；-ε为残差平均值；-sr为原始数列平均值；S1为原始数列标准差；S2为残差标准差；C为后验差比值；P为小误差概率。

主要的程序流程图如图1所示。

3 应用实例

3.1 数据来源

本文主要的数据来自福建统计局网站《福建统计年鉴》，主要的参考数据是2005—2013年福建省交通事故死亡人数，其中各个月份交通事故死亡人数如表2所示。

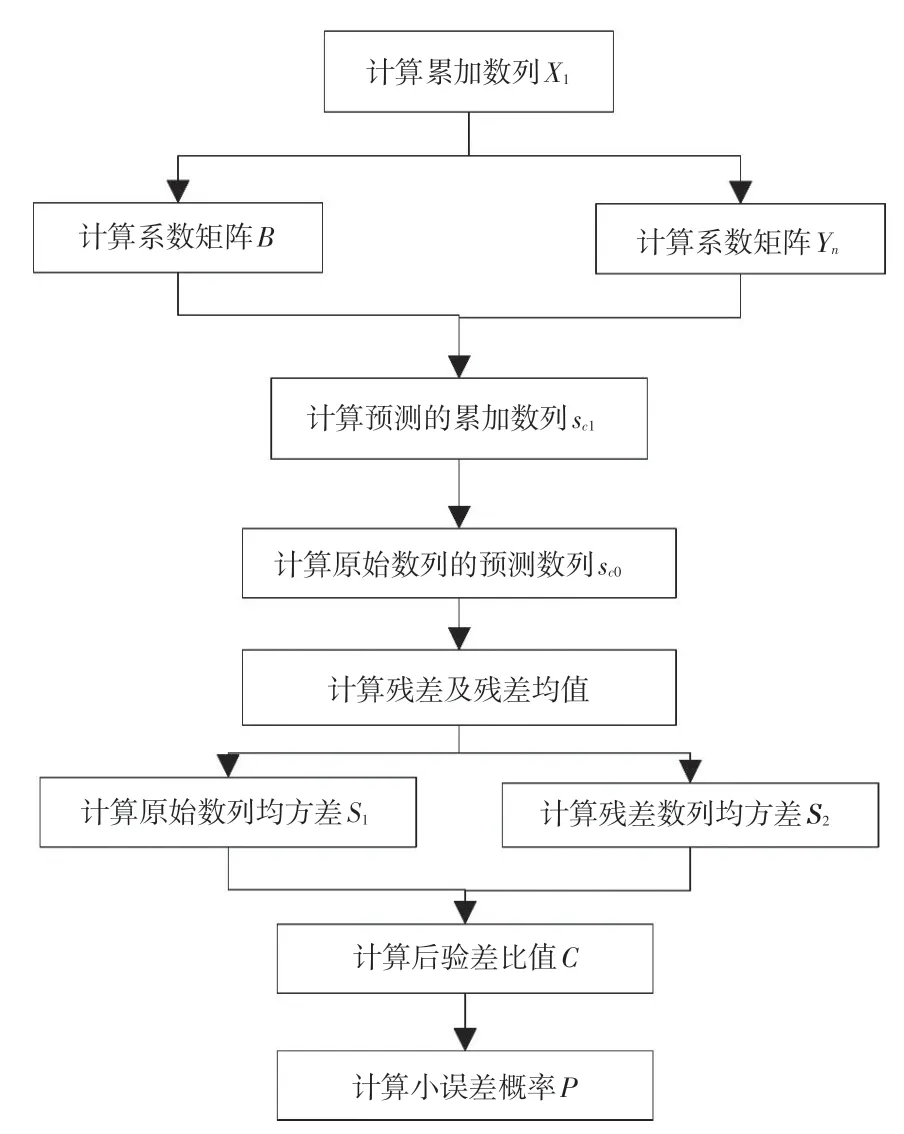
图1 MATLAB主要的程序流程

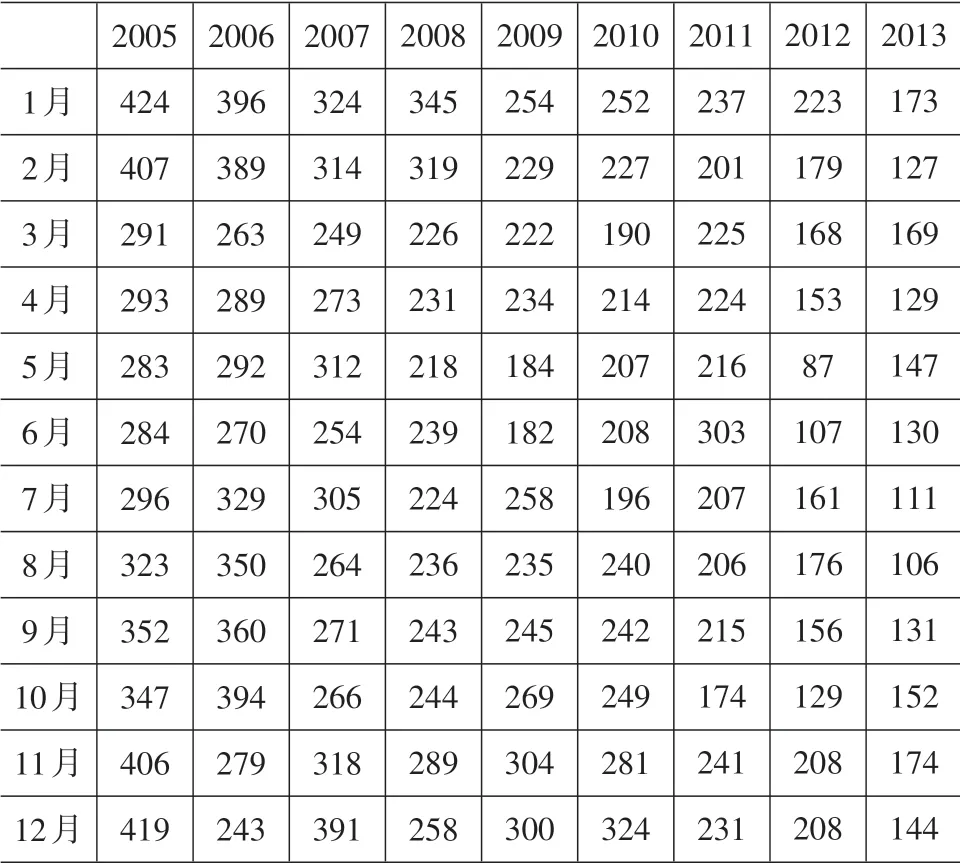
表2 福建省2005—2013年交通事故死亡人数数据统计

3.2 模型的建立

首先对原始数据进行区间的归类，分类结果如表3所示。

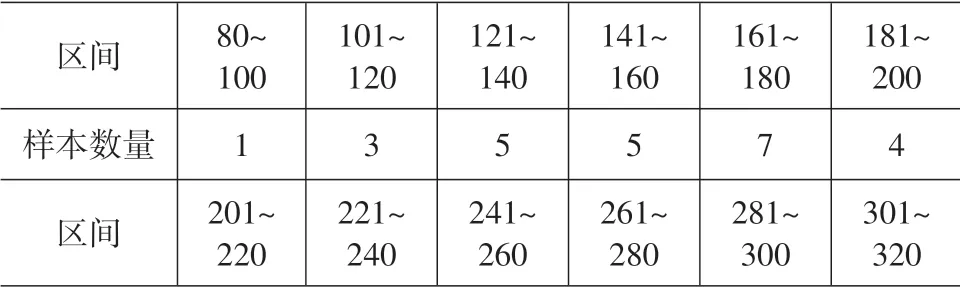
表3 数据区间归类

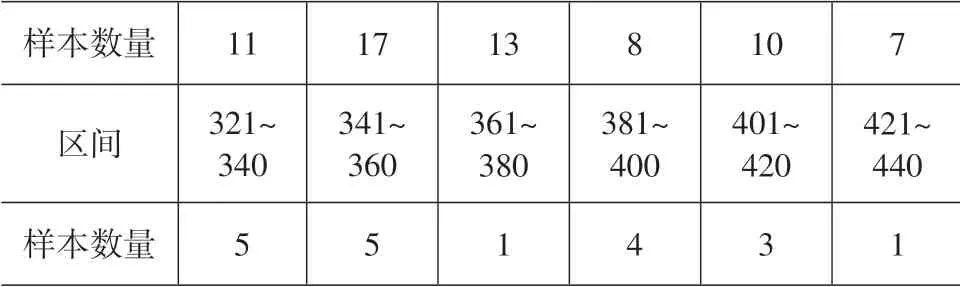
表3（续）

根据表3所呈现的区间特点，可知交通事故死亡人数主要集中在200～300之间，充分考虑这个区间特点，同时根据序列至少要有4个元素的GM（1，1）的模型要求，取下列9个阈值：

绘制原始数据的发展曲线以及各阈值的水平线，如图2所示。

图2 福建省交通事故死亡人数灰色拓扑图

3.3 数据处理

利用GM（1，1）模型的建模方法对以上的9组数据进行建模，并通过后验差法对所建的模型进行检验。这里以为例，应用灰色预测的方法进行预测。灰色预测主要借助MATLAB 语言来实现，主要的代码如下：

通过运行上面的代码，得到阈值为160时的预测模型为：

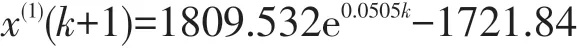
利用MATLAB 绘制原始数据与预测数据的曲线图，见图3。

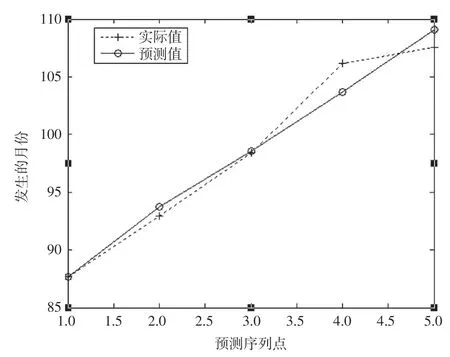
图3 阈值为160的实际值与预测值图

再利用MATLAB 对所得模型进行后验差检验，所得结果为C=0.0313，P=1，对照表1 的标准可知该模型的预测效果到达了良好的标准。

重复上述方法对其他阈值数列进行灰色预测和后验差检验，所得预测模型群及检验结果见表4。

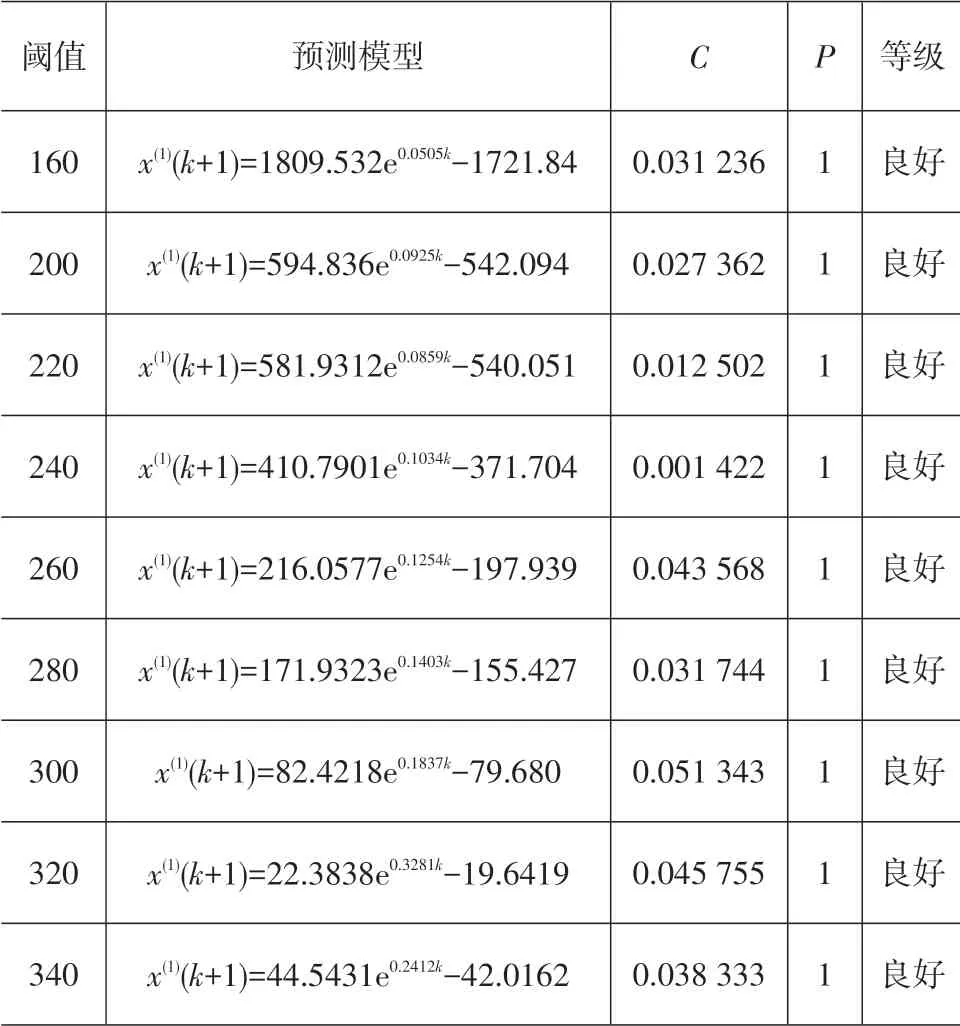
表4 灰色预测模型及后验差检验

通过表4可知，灰色预测模型的精确等级都为1级良好，表明该方法具有较高的适用性，可以直接用来对未来时刻进行预测。

利用表4的预测模型组对各阈值发生的时刻进行预测，得到的预测值如表5所示。

表5 各阈值预测模型所得到的预测结果

对表5中的数据进行处理，处理的原则主要有以下两点：

（1）在表5 的数据中，当小数部分小于0.5，则将此时刻归为当前的月份，当小数部分大于等于0.5，则将此时刻归为到下一个月。

（2）从表5可以看出，有些不同的阈值对应的预测值中出现同样的预测值，这样的点可认为是失效点，导致失效点出现的原因可能是多方面，所以对该类失效点并不能给出一个确定的预测值，只能用一个区间来描述。

通过对表5 数据的处理，得到各预测月份如表6。

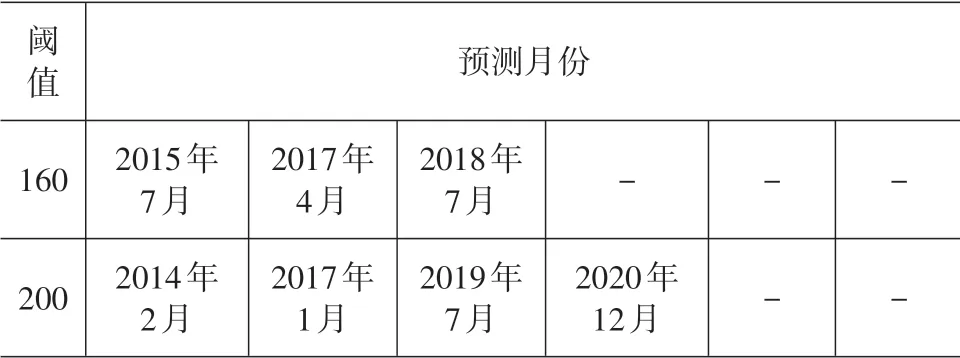
表6 各阈值预测模型所得到的预测月份

表6（续）

灰色拓扑预测在交通事故死亡人数预测中取得了较好的预测结果，通过运用MATLAB 编程使得计算过程变得更加简单，预测过程需要运用到较多的原始数据，预测结果的精确度较高，所以这种方法有较好的运用前景，对交通事故的管理以及相应的决策具有较大的意义。

4 结论

本文对福建省交通死亡人数采用了灰色拓扑的预测方法，并借助MATLAB 程序，对福建省2005—2013 年的交通事故死亡人数进行了研究。通过研究表明：福建省交通事故的死亡人数在年份上整体是呈现下降的趋势，说明近年来的交通事故得到了有效的控制，但是从月份上来看，每个月的死亡人数还是有较大的波动，灰色拓扑的预测方法有效地克服了数据波动大、没有明显的线性或曲线规律的特点。

拓扑预测是根据现有波形预测将来波形，所得到的结果也是在一定阈值内的波形，受到4个数据才能建模的条件的制约，最终得到的结果也只是在一定阈值内进行预测，不能系统地反映各个水平。灰色预测反映的结果是一种趋势，并不是特定的某个数字，交通事故的发生所涉及的因素随着时间环境的改变是动态变化的，所以在预测的时候要充分考虑到这点。

[1] 闫建华，宇仁德，汪洋.基于主成分分析的道路交通事故预测[J].交通标准化，2009（19）：86-90.

[2] 沈斐敏，陈伯辉，雷兢.基于人工神经网络的时间序列交通事故预测[J]. 福建工程学院学报，2005，3（4）：307-309.

[3] 王丽娟，查伟雄.基于支持向量回归机的道路交通事故预测模型研究[J].交通标准化，2010（11）：56-60.

[4] 房曰荣，沈斐敏.道路交通事故发展趋势分析与预测[J].中国安全生产科学技术，2012，3（8）：141-146.

[5] 胡启洲，高宁波，叶茂.基于支持向量机的道路交通事故数据统计模型研究[J].中国安全科学学报，2013，6（23）：39-44.

[6] 谢明芳，吴卢荣，许玉冬.特大交通事故动态分布拟合及灰色拓扑预测模型[J]. 延边大学学报，2013，3（39）：227-230.

[7] 姜学鹏，徐志胜.我国火灾起数的灰色拓扑预测[J].火灾科学，2006，2（6）：58-61.

[8] 石金泉，陆愈实，贾玉洁，等.基于Matlab的灰色模型在百万吨死亡率预测中的应用[J]. 安全与环境工程，2011，1（18）：77-80.

[9] 杨旭. 改进的灰色预测GM（1，1）模型的MATLAB 实现[J].江苏科技信息，2014（7）：69-70.

[10] 陈刚，于丹，吴迪. Matlab 基础与实例进阶[M]. 北京：清华大学出版社，2012.