模糊层次分析法模型在地铁区间隧道火灾风险评估中的应用

●周文科

(邵阳市消防支队，湖南邵阳 422000)

0 引言

伴随着城市化进程加快，世界各国的城市区域逐渐扩大，城市人口逐渐上升，城市在就业、环境污染、住房和交通等问题上面临严峻的挑战。为了缓解城市交通问题，我国一些大城市已经或正在着手修建地铁。地铁因其安全、舒适、载客量大、快速、准点、低耗能、少污染的特点，越来越受到人们的青睐。随着地铁的兴起以及人们对于生活质量要求的提高，地铁运营期间的消防安全也越来越受到人们的重视，尤其是地铁隧道，由于其绝大多数为建设在地下的狭长空间，一旦发生火灾，危害特别大，人们对于地铁区间隧道内的火灾危险性也越来越关注，因此迫切需要一种方法对地铁区间隧道的火灾风险进行评估。

1 模糊一致性矩阵介绍

目前针对地铁火灾风险评估的研究相对较少，由Satty［1］提出的层次分析法是风险评估最常见的一种方法，大多数从事火灾风险评估的学者的研究都是围绕着层次分析法展开的。但是在使用该方法时，存在着较多未解决的难题［2］，主要体现在以下几个方面:首先是目前普遍使用的判断标准CR＜0．1缺乏科学依据;其次是在具体计算过程中需要反复地进行调整、检验;最重要的一点是判断矩阵的一致性与人类思维的一致性有一定的差异。

国内曾有学者针对模糊一致矩阵在决策中的运用进行了大量的研究［3］，有部分学者针对模糊一致矩阵、模糊一致关系以及去模糊化进行了研究［4］，此后有学者针对模糊一致矩阵在多层次、多因素决策方案优选中的应用进行了研究［5］，并取得了一系列成果。故本文引入了模糊一致性矩阵，其中一致性矩阵满足如下条件:

模糊一致性矩阵 R=(rij)n×n满足:∀i，j，k 有:

在模糊判断矩阵中，矩阵R中的数值通过如下方式及准则来确定［6］:(1)∀i(i=1，2，…，n)，有 rii=0．5;(2)∀i，j(i，j=1，2，…，n)，有 rij+rji=1;(3)从R中划掉任意一行及其对应的列所得的子矩阵仍然是模糊一致矩阵;(4)模糊互补矩阵R是模糊一致性矩阵的充要条件是任意两行的对应元素之差为常数;(5)模糊互补矩阵R是模糊一致性矩阵的充要条件是任意指定行和其余各行对应元素之差为某一常数。

遵照以上原则构造层次分析法的判断矩阵时，可以满足层次分析法判断矩阵一致性标准，确定权重之后无需进行一致性检验。

根据文献［7-8］可知在得到模糊一致性矩阵后，根据模糊一致判断矩阵的元素与权重的关系式(2)、(3)得出各因素权重，达到去模糊化目的。

其中，a≥(n-1)/2。

2 地铁区间隧道火灾风险模型

通过对地铁相关资料的大量调查，火灾的发生及损失情况主要受地铁区间隧道的建筑特性、抗火、灭火能力，列车的抗火、灭火能力和地铁运营公司的运营管理能力及消防队的灭火能力等一系列因素的制约。

2．1 地铁火灾层次结构模型建立

通过对地铁致灾机理、灭火过程及灾后救援的研究分析，构建了地铁火灾层次分析法结构模型，如图1所示。

图1 地铁隧道火灾风险评估结构模型

2．2 基于专家评分的模糊一致性矩阵的建立

通过与专家评分过程相结合，由上至下，确定每层指标的层次分析法判断矩阵。如图1所示四层层次结构，分别有如下因素集:第一层地铁区间隧道危险性为目标层，第二层 {B1，B2，B3}为准则层，{C1，C2}为 B1的子评价指标集，{D1，D2，…，D7}为 C1的子评价指标集。其中{D1，D2，…，D19，D20}为指标层，其权重为(ω1，ω2，…，ω19，ω20)。通过专家评分及模糊矩阵的性质，获得模糊一致性矩阵。

对各个准则层和指标层进行两两比较，形成层次分析法的判断矩阵，其中专家评分标度如表1所示［9］。

表1 专家评分标度方法说明表

进行两两比较可以得到模糊一致性矩阵的对比矩阵为:

准则层模糊一致性判断矩阵

地铁隧道特性模糊一致性判断矩阵

运行列车特性模糊一致性判断矩阵

消防灭火设施模糊一致性判断矩阵

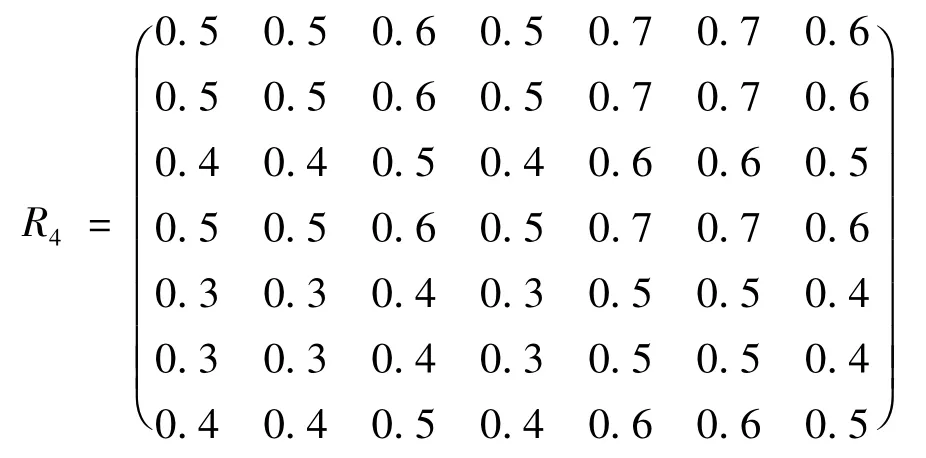
消防队灭火模糊一致性判断矩阵

2．3 地铁系统各子因素性能评价权重

对于模糊一致性矩阵R1～R5，根据模糊一致性矩阵及层次分析法的性质，可以得出各个模糊矩阵的权重，R1的权重向量为:

同理，可以得出R2～R5的权重向量为:

通过对地铁系统的模糊一致性矩阵处理及层次化分析，可以得出地铁各子因素的性能权重向量为:ω = (0．017，0．035，0．023，0．029，0．023， 0．023，0．035，0．036，0．073，0．073，0．120，0．146，0．038，0．038，0．031，0．038，0．023，0．023，0．031， 0．053，0．053，0．039)

3 某地铁火灾风险量化评估

建立模糊判断矩阵求得权重后，还不能对地铁区间隧道火灾风险进行判定，仍然需要借助风险指数法进行量化处理。结合火灾风险指数法，通过计算被评价对象的安全分，确定地铁区间隧道的安全性，具体计算如下式所示:

其中，wi为权重系数;Pi为各参数得分。

结合某地铁具体情况、相关法律法规(如《地铁设计规范》)和人员对于地铁消防安全的预期，对每个指标因素进行等级划分，每个等级体现该因素在所评价的对象中所处的安全状态，并赋予相关分值。

本文将具体的评分划分为优、良、中、差四个等级［10］，具体见表2。

表2 指标评价尺度和系统评价等级

以某地铁隧道为例，该地铁中设置了火灾自动报警系统，内部配备了完善的灭火器、消火栓、气体自动灭火装置、应急照明，通风排烟系统能够正常工作;列车的可靠性较高，列车内的座椅、线缆等采用无毒不燃材料。隧道内的疏散设施能满足人员疏散;消防配备情况良好。此外，该隧道管理公司有较严格的消防安全管理制度。

通过对地铁区间隧道消防系统各个因素的打分结果，进行火灾安全风险评价，计算出地铁区间隧道的火灾风险评估量化值为81．875分，与评价等级表对比可以看出，该隧道火灾风险等级控制在良好的范围内。

4 结论

本文针对地铁安全问题，通过对模糊一致性矩阵及层次分析法分析，建立了模糊层次分析法评估模型，确立了地铁区间隧道评价指标体系，建立了一种较合理的地铁区间隧道火灾风险评估模型;通过对地铁区间隧道火灾风险评估，可以得出如下结论及建议:

4．1 利用模糊层次分析法模型，能够有效地弥补传统的层次分析法的缺陷，为地铁建设、运营的安全提供可靠的依据;同时也能够获取地铁区间隧道中火灾安全较重要的环节，便于地铁运营时给予足够的重视。

4．2 由评估结果可以看出，地铁火灾中占据最大比重的还是地铁消防方面的硬件设施，包括隧道自身特性和消防设施;故在隧道设计、施工期间应做好地铁隧道消防安全论证。

4．3 通过对地铁区间隧道风险评估，可以看出消防安全管理所占的权重值较高;故在地铁正常运营中，不仅需要建立完善的安全管理制度，更要建立完善的巡查制度，保证安全管理制度的实施。

4．4 此模型仍然有较多的不足之处，首先是对于模糊函数去模糊化过程中有诸多不足，另外在地铁区间隧道指标体系建立过程中也存在不周到之处，需要进一步完善。

［1］ SAATY T L．The Analytic Hierarchy Process［M］．New York：McGraw-Hill，1980．

［2］张吉军．模糊层次分析法(FAHP)［J］．模糊系统与数学，2000，14(2)：80-88．

［3］姚敏，黄燕君．模糊决策方法研究［J］．系统工程理论与实践，1999，19(11)：61-64．

［4］姚敏，张森．模糊一致矩阵及其在决策分析中的应用［J］．系统工程理论与实践，1998，18(5)：78-81．

［5］黄健元．模糊一致矩阵在多层次、多因素决策方案优选中的应用［J］．河海大学学报：自然科学版，1999，(5)：84-89．

［6］蒋良奎．模糊一致矩阵在层次分析法中的应用［J］．上海海运学院学报，1998，(2)：57-62．

［7］吕跃进．基于模糊一致矩阵的模糊层次分析法的排序［J］．模糊系统与数学，2002，(2)：79-85．

［8］张吉军．模糊一致判断矩阵3种排序方法的比较研究［J］．系统工程与电子技术，2003，25(11)：1370-1372．

［9］林钧昌，徐泽水．模糊AHP中一种新的标度法［J］．运筹与管理，1998，(2)：39-42．

［10］朱祖斌，张瑞芳．层次分析法在烟草物流配送中心火灾危险性评价中的应用［J］．中国烟草科学，2013，(2)：104-107．