基于二自由度模型的无人驾驶车辆轨迹跟踪控制研究
秦万军,徐友春,李明喜,耿 帅,李欣莹
(1.军事交通学院 研究生管理大队,天津300161;2.军事交通学院 军用车辆系,天津300161)
无人驾驶车辆是轮式移动机器人的一种,在未来智能交通系统中有着广阔的应用前景。它是一个集环境感知、规划决策和多级辅助驾驶等功能于一体的综合系统,涉及信息工程、计算机科学、控制科学等诸多领域,是一个国家智能化水平的重要标志[1],已经成为当下研究的热点。其中,轨迹的跟踪控制[2]是实现无人驾驶功能的关键技术之一。本文以无人驾驶车辆线性二自由度模型为基础,对车辆轨迹的跟踪控制进行相关研究,设计并实现了轨迹的跟踪。
1 模型的建立
1.1 车辆坐标系的建立
车辆坐标系(如图1 所示),指的是固结于运动着的车辆上的动坐标系,车辆的运动多借助于此坐标系来描述。XOZ处于车辆左右对称的平面内,坐标系的原点O与质心重合,X轴平行于地面指向车辆运动方向,Y轴指向驾驶员的左侧,Z轴通过车辆质心垂直指向上方。

图1 车辆坐标系
1.2 线性二自由度模型的建立
1.2.1 模型的假设条件
(1)无人驾驶车辆的车轮、车体及道路均视为刚体。
(2)忽略悬架的作用,认为无人驾驶车辆只进行平行于地面的运动。
(3)无人驾驶车辆沿X轴的前进速度u视为不变,且侧向加速度限定在0.4g以下。
这样,把无人驾驶车辆简化成一个2 轮摩托车模型(如图2 所示)。它是一个具有侧向及横摆运动的二自由度模型。
1.2.2 轮胎侧偏力的计算
忽略轮胎的非线性(侧偏角不大于5°)因素,计算前、后轮胎受到的侧向反作用力(即侧偏力):

式中:α1、α2分别为前、后轮的侧偏角;k1、k2分别为前、后轮胎的侧偏刚度。
车辆前、后轮的侧偏角与其运动参数有关。如图2 所示,质心的侧偏角为β(β=v/u),车辆前、后轴中点速度分别为u1、u2,侧向速度为v,ξ 为u1与X轴的夹角,其值为

图2 车辆二自由度模型
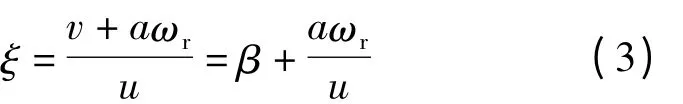
根据坐标系的规定,前、后轮的侧偏角为
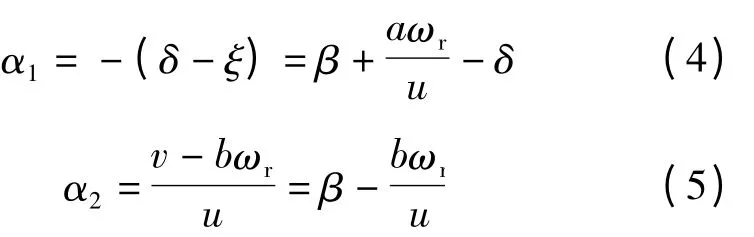
式中:a、b为质心到前、后轮的距离;ωr为车辆的横摆角速度;δ 为前轮侧偏角。
由此,得前、后轮分别受到的侧偏力为
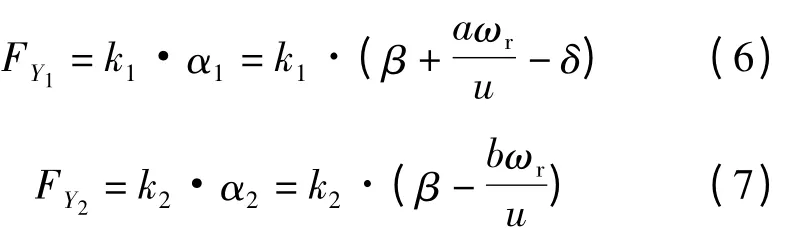
1.2.3 运动微分方程的推导
根据上述受力分析,考虑车辆的侧向和横摆2个运动,可以列出车辆受到的外力沿Y轴方向的合力与绕质心的力矩的方程:
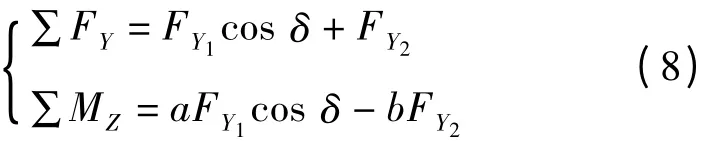
由刚体的转动定律得

式中IZ为车辆绕质心的转动惯量。
由牛顿第二定律得
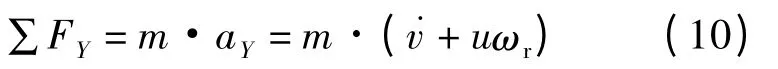
整理后可以得车辆二自由度运动微分方程:
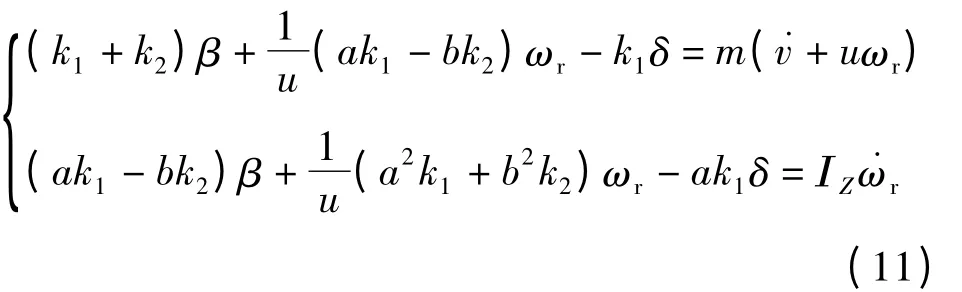
1.2.4 车辆运动方程的推导
如图3 所示,OX与OY分别为车辆坐标系的纵轴和横轴。在t时刻质心的速度v1在ox轴、oy轴的分量分别是u、v。因为车辆在转向行驶时往往伴随着平移和转动2 种动作,所以车辆坐标系中的质心速度大小与方向均发生变化,因而车辆坐标系的纵轴与横轴也随之发生变化。可以推导出车辆在绝对惯性坐标系下的运动方程:

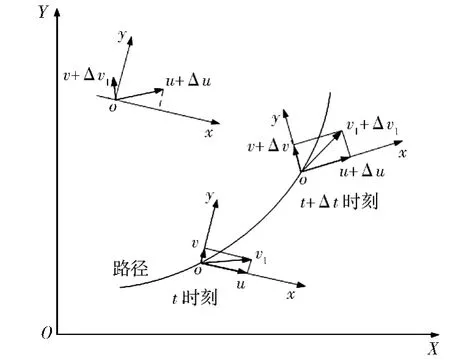
图3 车辆运动分析
2 基于二自由度模型的Matlab/Simulink 仿真
式(11)给出了车辆的二自由度运动微分方程,此方程包含了最重要的车辆轮胎侧偏刚度与质量2 个方面的参数,所以能够较好地反映车辆转向运动的最基本的特征。基于此模型,下面用Simulink 进行仿真分析。
2.1 车辆动力学模型仿真
Simulink 是Matlab 软件的扩展,它是一个实现动态系统建模和仿真的软件包,而且具有相对独立的功能和使用方法。该无人驾驶车辆系统参数见表1。把前轮转角作为输入量,可以很方便地控制车辆的运动状态,让车辆尽可能地跟随预期的轨迹行驶。由此,可以建立Simulink 仿真流程(如图4 所示)。

表1 无人驾驶车辆系统参数
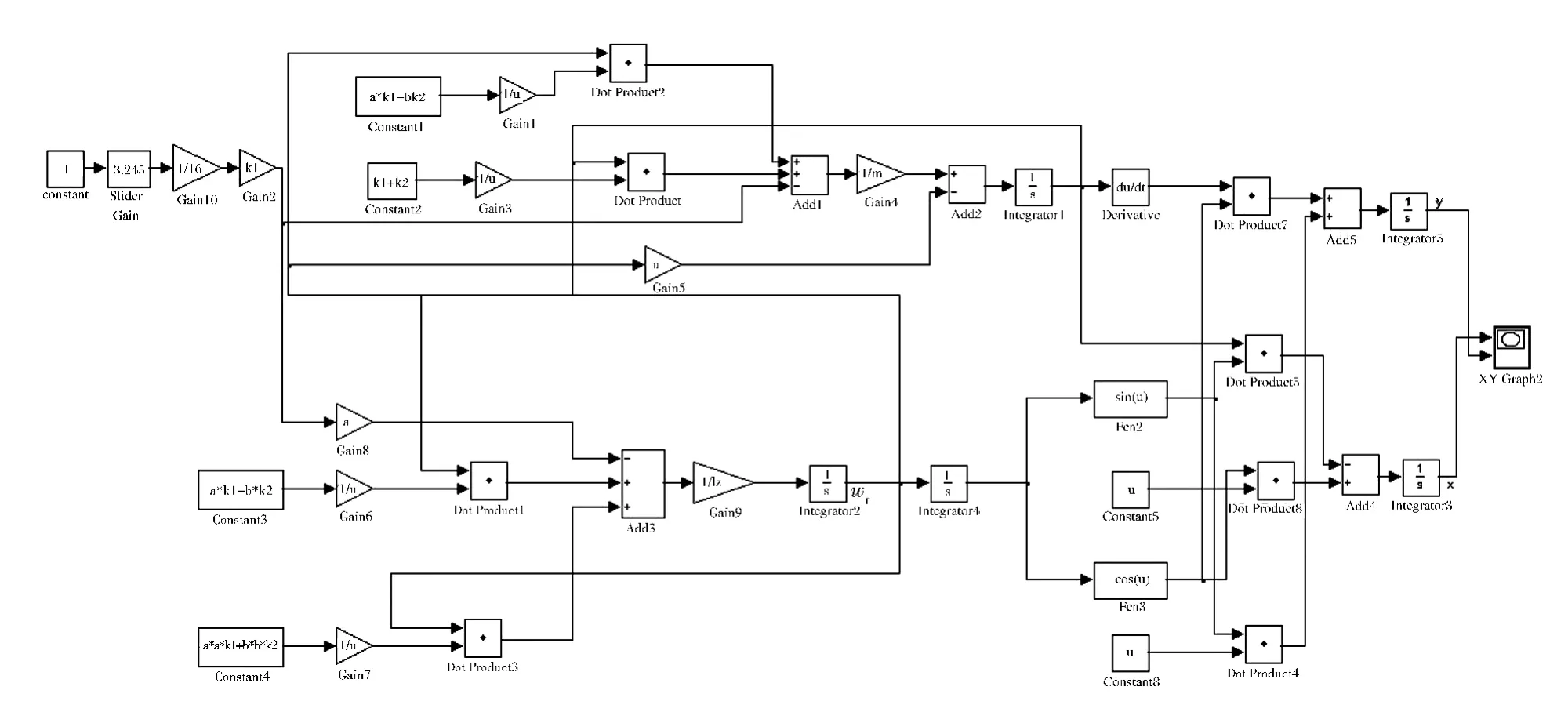
图4 车辆二自由度模型仿真流程
按图4 所示连接好模块后,按表1 设置好系统的仿真参数,运行后可以得到ωr随时间的变化曲线(如图5 所示)。
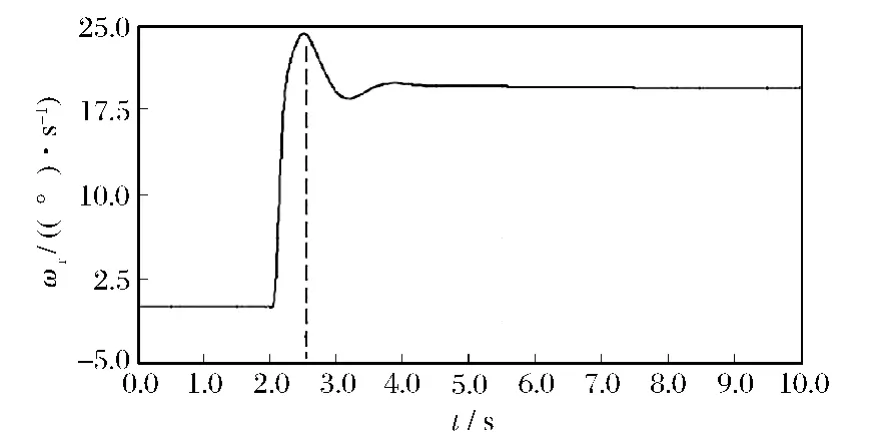
图5 横摆角速度随时间的变化曲线
本模型是以车辆横摆角速度ωr来描述车辆响应的。由图5 可以看出,在t=0 时,ωr=0,在t=2 s时,给车辆以转向盘角阶跃输入后,车辆横摆角速度经过一个过渡过程后达到稳定。
2.2 无人驾驶车辆转向仿真实例
为验证本文提出模型的有效性,利用Matlab优化工具箱对无人驾驶车辆转向动作进行仿真。
图6(a)是典型的转向动作仿真结果。可以看出,转向的轨迹具有连续的平滑轮廓。为说明转向过程中各种动力学参数,图6(b)—(d)分别给出了各种状态量的仿真结果。从这些状态量的变化情况可以看出,它们都能达到稳定状态,且具有良好的连续性,表明该模型是有效的。
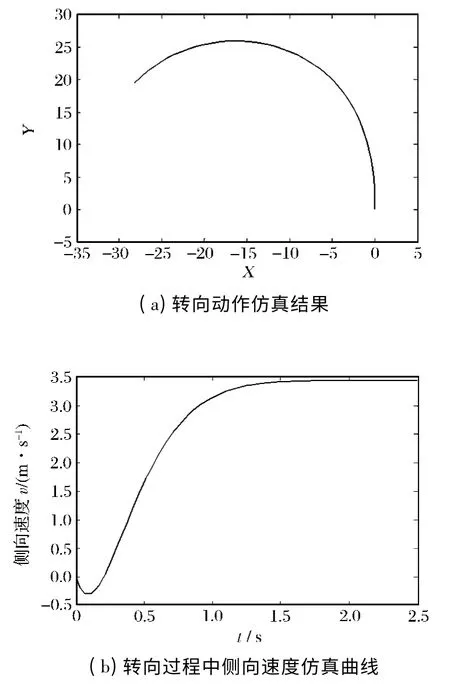
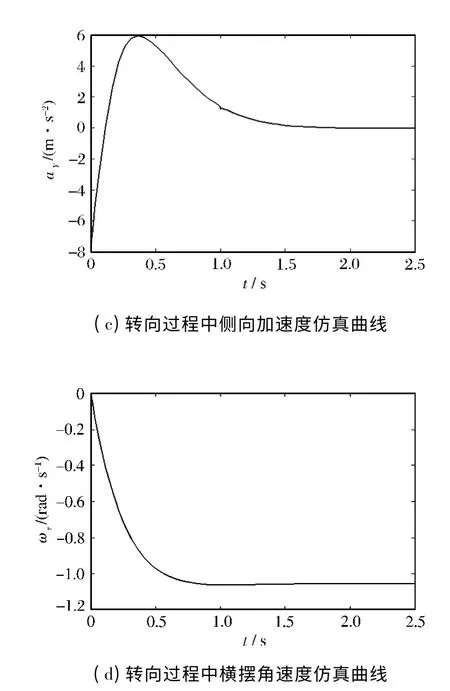
图6 无人车转向过程中各状态参量仿真结果
3 轨迹的跟踪控制
3.1 期望轨迹的生成
无人驾驶车辆研究的一个最基本的问题就是轨迹的跟踪控制问题[3],这问题解决不了,就会制约无人驾驶车辆的发展。一个工作状况良好的无人车驾驶系统,它的控制特性应该与熟练并且有高超的驾驶技术的驾驶员的操纵行为保持基本一致[4]。而轨迹的跟踪需要驾驶员对驾驶信息(如前方道路曲率等)及汽车在道路上的方位进行辨识,并以此为依据调整转向盘转角进行合适的方向控制。本文通过GPS,采集了一系列的路径集,通过Matlab 中“plot(Gps1,Gps2)”的命令,可以得到一条无人驾驶车辆的期望轨迹。
3.2 GPS 坐标与大地坐标的转换
现在GPS 所采用的是美国国防部1984 世界坐标系,简称为WGS-84,它是一个协议地球参考系,地球的质心是坐标系的原点。在本文的数据处理中,需要计算地球两点直接的精确距离(弧长),直接用经度和纬度计算两点间距离时主要考虑2 个参数,即经、纬度平均每一度的距离(弧长)[5]。纬度平均每一度的弧长大概是相等的,约为111 km,而经度平均每一度的弧长是随着纬度的变化而变化的,纬度越小经向的弧长越大,相反,纬度越大经向的弧长就越短。
每一纬度所在经向1°的弧长计算如下:
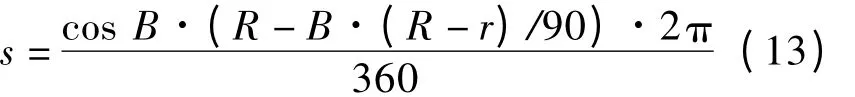
式中:B为计算点所在的纬度(取到度)值;R为赤道的半径(取R=6 378 137 m);r为极轴的半径(取r=6 356 752 m)。
3.3 GPS 坐标转换后的仿真
由上述计算可得,GPS 坐标中的1°代表实际距离约为111 km,而模型的运动是在车辆坐标系下的,把车辆坐标系的度量缩小111 000 倍,它的量纲就会与GPS 坐标系保持一致。因此,在车辆模型输出的X、Y处加入一个增益模块,让模块参数值取1/111 000,把实际的坐标转换到GPS 坐标系中。根据采集到的GPS 数据,无人驾驶车辆的起始位置为东经117.257 076°、北纬39.136 586°。由于车辆在绝对坐标系下的坐标原点为(0,0),相当于赤道中心,分别给横、纵坐标加入一个偏移量,取无人驾驶车辆起始位置的经纬度坐标值作为偏移的幅度值。如此,车辆模型的车辆坐标系的原点就会和获得的转向轨迹的起点重合。建立仿真图如图7 所示。

图7 无人车转向轨迹跟踪控制仿真
图7 仿真图中的Slider Gain2 模块的作用就相当于转向盘,通过改变它的正负及大小就可以控制车辆的转向。而人眼是最好的预瞄跟随控制器,根据已经由GPS 规划好的轨迹,慢慢改变Slider Gain2 模块的参数值,让车辆的实际运动跟随期望的轨迹运动,这样就可以很好地实现轨迹的跟踪控制。仿真结果表明(如图8 所示),通过该模型的控制,车辆的实际轨迹(实线)与期望轨迹(虚线)能够比较好地重合在一起,误差在可以接受的范围内,表明该模型是有效、可控的。

图8 无人驾驶车辆转向轨迹跟踪控制仿真结果
4 结 语
通过对车辆前、后轮胎所受的侧偏力进行分析,求解出车辆的运动微分方程,并基于此建立一个二自由度模型;用Matlab/Simulink 软件对提出的模型进行仿真,通过实例验证表明,该模型是有效性的,具有较好的鲁棒性。
本文利用GPS 采集的点建立一条预期轨迹,通过车辆的动力学模型对车辆的前轮转向角进行控制,使车辆按该期望的轨迹进行运动,初步实现了轨迹的跟踪,为无人驾驶车辆轨迹跟踪控制,尤其是基于GPS 坐标点的轨迹跟踪控制提供了理论上的支持。
[1] Morita T,Broggi A,Fascioli A,et al. An Approach to the Intelligent Vehicle[C].1993 IEEE Intelligent Vehicles Symposium,1993:426-432.
[2] 刘子辉. 军用无人驾驶车辆非结构化道路识别方法研究[D].长春:吉林大学,2007.
[3] CHRISTENSEN H I.Localization and navigation of a mobile robot using natural point landmarks extraceted from data[J]. Robotics and Autonomous Systems,2000,33(3):131-142.
[4] 高振海,管欣,郭孔辉. 预瞄跟随理论和驾驶员模型在汽车智能驾驶研究中的应用[J]. 交通运输工程学报,2002,2(2):63-66.
[5] 黎珍惜,黎家勋.基于经纬度快速计算两点间距离及测量误差[J].测绘与空间地理信息,2013,36(11):235-237.

