BP与小波神经网络短时交通流预测对比研究

王 健 孙结松

（江苏纬信工程咨询有限公司，江苏 南京 210014）

0 引言

随着经济、社会的发展，越来越多的人选择使用小汽车出行，导致城市交通压力迅速增大，许多大城市如北京、上海的交通不堪重负，好在近年来很多国内的学者开始急切关注交通问题，提出很多解决的方案。智能交通系统（intelligent transportation system，ITS）作为一种实时、高效、准确、便民的交通系统开始作为解决交通问题的新手段进入人们的视野，很多专家预言未来要想缓解城市交通压力，ITS 具有非常重要的作用。

交通流预测是城市交通控制和诱导的基础。只有在全面提前掌握城市各路段交通动向，决策人员才能据此做出准确的判断，合理调配交通流。交通流预测是指根据现有的交通流数据，预测下一时刻（最多为5min）的交通流量、交通速度、交通密度。本文重点研究如何预测下一时刻（取15min）交通流量。

短时交通流预测研究受到广泛关注，现已发展了很多成熟的理论方法。典型的预测方法是以统计分析方法为基础，但由于短时交通流往往具有迅速而剧烈波动且体现频繁的交通拥堵的特征[1]，所以短时交通流数据常常是非线性的，通过数据分析，其非线性特征在早晚高峰期尤为明显。所以这些以线性预测为基础的方法往往预测精度不高，结果不理想。为适应短时交通流变化的非线性性，出现了一些改进的模型，比较成功的是卡尔曼滤波等方法。

随着数学研究的进展，许多非线性理论方法被应用于短时交通流预测，针对短时交通流变化的随机性和非线性性，出现了以神经网络、模糊理论、混沌理论和元胞自动机等非线性系统理论为基础的非线性预测模型[2]，也有一些学者通过仿真和神经网络相结合的方法对此进行深入研究[3]。由于小波神经网络可避免BP 神经网络等结构设计上的盲目性，并且网络权系数线性分布和学习目标函数的凸性，使网络训练过程从根本上避免了局部最优等非线性优化问题，同时兼有较强的函数学习和推广能力[4]，固本文重点研究基于小波神经网络的短时交通流预测，并对比BP 神经网络，以比较两者的差异。

1 小波神经网络

1.1 小波理论

小波分析是针对傅里叶变换的不足发展而来，小波变换经常和傅里叶变换做比较，在那里信号用正弦函数的和来表示。主要的区别是小波在时域和频域都是局部的，而标准的傅里叶变换只在频域上是局部的。短时距傅里叶变换(Short-time Fourier transform)(STFT)也是时域和频域都局部化的，但有些频率和时间的分辨率问题，而小波通常通过多分辨率分析给出信号更好的表示。小波变换计算复杂度上也更小，只需要O(N)时间，而不是快速傅里叶变换的O(N log N)，N 代表数据大小[5]。

1.2 小波神经网络

1.2.1 小波函数构建

小波神经网络是一种以BP 神经网络拓扑结构为基础，把小波基函数作为隐含层节点的传递函数，信号前向传播同时误差反向传播的神经网络。设x（k）为小波神经网络的输入参数向量，Y（m）是小波神经网络预测输出向量，ωij 和ωjk 为小波神经网络权值。

则隐含层输入计算公式为：

式中h(j)为隐含层第j 个节点输出值；ωij 为输入层和隐含层连接权值；bj 为小波基函数hj 的平移因子；aj 为小波基函数hj 的伸缩因子；hj 为小波基函数。

本文采用的小波基函数为Morlet 母小波基函数，数学公式为：

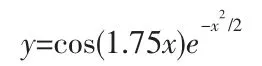
函数图形如图1：

图1

小波神经网络输出层计算公式为：

式中ωik为隐含层到输出层权值；h(i)为第i 个隐含层节点的输出；l为隐含层点数；m 为输出层节点数。

1.2.2 小波神经网络参数修正

小波神经网络权值参数修正类似于BP 神经网络权值修正算法，采用梯度修正法修正网络的权值和小波基函数参数，从而使小波神经网络预测输出不断逼近期望输出。修正过程如下：

（1）计算网络误差

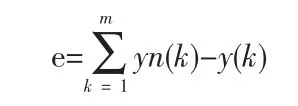
式中yn(k)为实际输出；y（k）为小波神经网络预测输出。

（2）根据预测误差e 修正小波神经网络权值和小波基函数系数

式中，η 为学习速率。

1.2.3 小波神经网络算法步骤

步骤1：网络初始化。随机初始化小波函数伸缩因子ak、平移因子bk以及网络连接权值ωij、ωjk，设置网络学习速率。

步骤2：计算预测输出、网络实际和预测误差e。

步骤3：权值修正。根据误差e 修正网络权值和小波函数参数，使网络预测值逼近实际值。

步骤4：判断算法是否结束，如果没有，返回步骤2。

1.3 小波神经网络预测短时交通流量

（1）建立如图1 所示神经网络模型。

（2）根据得到的交通流量数据样本，进行数据处理，并选择一部分作为训练样本，一部分为测试样本。

（3）利用训练样本对网络进行训练，隐含层函数采用小波函数。

（4）利用训练好的网络进行预测，并比对实际交通量。

图2 小波神经网络模型

2 实例分析

预测实例所采用的数据采自南京市交管局调查的某关键路段流量。有288+96 组数据样本。其中每组数据间隔15min，前288 组用于训练网络，后96 组用于测试网络准确性。

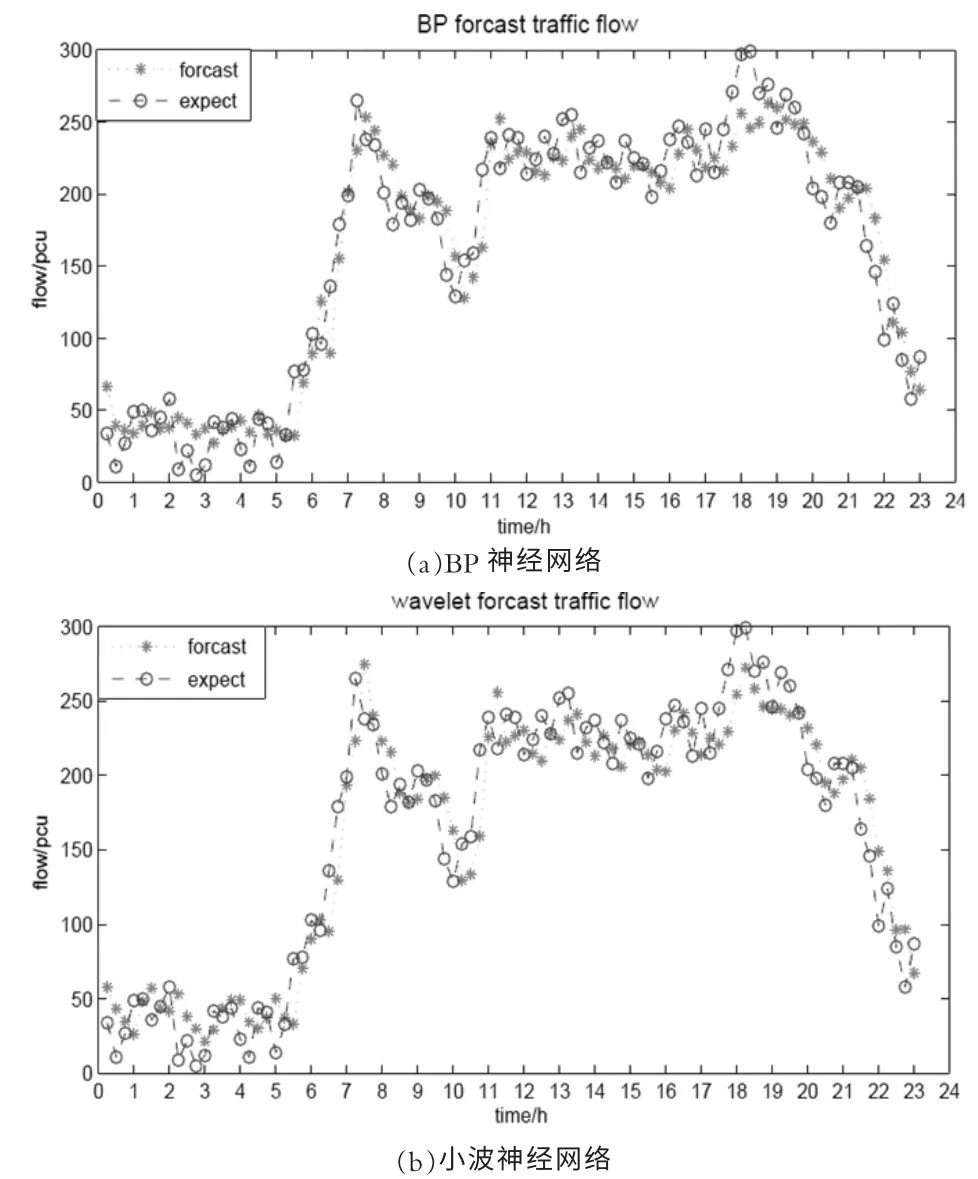
图3 神经网络预测输出

2.1 BP 与小波神经网络预测结果

传统BP 神经网络目前已较为成熟[6]，构建结构为4-5-1 的三层BP 网，利用Matlab 神经网络工具箱newff、sim、train 三个主要函数进行预测。由于是对比小波神经网络的准确性，所以并没有对这些函数的参数进行讨论和改变，均采用默认值。小波神经网络设计三层网络，分别为4 个节点的输入层、6 个节点的隐含层、一个节点的输出层。

根据上述理论，两者预测流量与实际流量如图3、预测误差如图4，误差百分如图5。

图4 神经网络预测误差

图5 神经网络预测误差百分比

2.2 预测准确性分析

由两种方法预测的流量对比实际流量分析可得，在6：00-22：00 这个时段预测较为准确，这段时期相比其他时间段交通量较大，是人们出行活动的主要时期，在这个时间段预测准确是至关重要的。夜间（22：00-6：00）这段时期可能车流较少，随机性较大，造成预测的误差加大。本文没有更多数据检验，实为一种遗憾。综上来看，神经网络在预测短时交通流时具有较高的准确性。

定性的分析预测方法的准确性还不够，为了检验各种方法的预测精度，本次案例误差结果对比指标采用平均绝对误差（mean absolute deviation，MAD，表示预测值与实测值得实际偏差绝对值的均值）、平均绝对百分比误差（mean absolute percentage error，MAPE，表示预测值与实测值得实际偏差绝对值占实测值百分比的均值）。

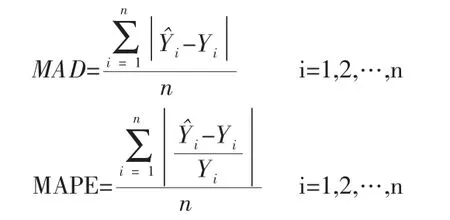
MAD 与标准偏差类似，但更容易求的。MAD 能较好的反映预测的精度，但它不容易衡量无偏性。MAD 与MAPE 常用来衡量预测误差，但单一的指标很难全面地评价一个预测模型，所以本次这2 个指标全部选用来检验预测精度。

本次BP 神经网络和小波神经网络的MAD 与MAPE 指标如表1 所示。

由表1 可以看出，两种方法预测的交通量误差在20 左右，相比人们活动时期的交通量不算太大，MAPE 如此高是由于部分时间车流较小，预测误差百分比很容易超过1。总体来说小波神经网络优于BP 神经网络，但优势不明显，可选用其他母小波做隐含层基函数或使用增加动量项修正网络参数的算法，来提高网络学习效率。

3 结论

本文主要分析了小波变换的特点、原理，并以Morlet 母小波作为神经网络隐含层基函数构建了小波神经网络，对数据进行预测分析，并比对了传统的BP 神经网络，发现神经网络作为一种新型预测技术，具有一定的准确性，但无论是BP 神经网络还是小波神经网络都不够完善[7]，短时交通流预测作为未来交通管理的基础，今后还应有越来越多的神经网络模型应用在交通流预测上，发展更适合的算法以得到更准确的预测结果。

［1］孙湘海，刘潭秋.基于非线性时间序列模型的城市道路短期交通流预测研究[J].土木工程学报，2008(1)：104-109.

［2］邵春福，熊志华，姚智胜.道路网短时交通需求预测理论、方法及应用[M].北京：清华大学出版社，2011.

［3］沈颖洁，韩宝睿，刘英丽，等.基于仿真的隧道检测器优化布设及短时交通流预测[J].公路交通科技，2014，1：124-130.

［4］蔡念，胡匡祜，李淑宇，等.小波神经网络及其应用[J].中国体视学与图像分析，2001，12(4)：239-245.

［5］侯霞.小波神经网络若干关键问题研究[D].南京航空航天大学，2006.

［6］王吉权.BP 神经网络的理论及其在农业机械化中的应用研究[D].沈阳农业大学，2011.

［7］田晶，杨玉珍，陈阳舟.短时交通流量两种预测方法的研究[J].公路交通科技，2006（4）：104-106.