2011年日本东北MW9.0地震：GPS与强震数据的比较

汪荣江 S.Parolai 葛茂荣 金明培 T.R.Walter J.Zschau

引言

地震引起的瞬时和永久地面运动，对震源定位及破裂过程的研究具有非常重要的作用。通常情况下，瞬时和动态运动由布设在全球的地震传感器测量，产生速度或加速度地震图，而永久位移则传统上通过大地测量方法测量得到。

一方面，全球定位系统（GPS）硬件的不断快速发展和GPS数据处理策略的改进，使得从高速GPS估计地震位移已成为研究课题，并称为GPS地震学（如：Larson et al，2003；Bock and Prawirodirdjo，2004；Chen et al，2004；Langbein and Bock，2004；Miyazaki et al，2004；Elósegui et al，2006；Larson，2009；Irwan et al，2011）。当前，GPS地震学的中心工作是采集高速GPS数据和改进处理方法（Smalley，2009）。另一方面，最近的研究表明，大的近源静态位移也可以从经验基线校正后的高质量加速度仪记录得到（如：Graizer，1979，1983；Iwan et al，1985；Boore，2001；Wang，Boore，et al，2003；Wu and Wu，2007；Chao et al，2009；Wang et al，2011）。因此，由于GPS和强震仪器的互补优点，联合使用二者可以改善数据覆盖，可以提高数据处理新策略的发展（Emore et al，2007；Bock et al，2012）。然而，截至目前为止，仍未实现对这种数据流系统性的测试和比较，以及它们对运动学震源模型联合影响的研究。

日本是世界上GPS观测网和地震台网分布最密集的国家之一，当前包括有1 200个GPS永久观测站的GeoNet、有84个宽带地震台站的F－Net、有1 000个强震观测台站的K－NET、有777个高灵敏度地震台站（井下安装）的 Hi－Net，以及与 Hi－Net台站同址布设的KiK－Net。在 KiK－Net的每个台站，装配有两台强震观测仪，分别装在地表和井下（见数据与来源一节）。同时对其他数据，如InSAR数据，也进行采集，但本文未作进一步的讨论。尽管如此，在2011年东北MW9.0地震发生后，从这些观测台网获得了空前数量的地震动数据，为评估不同观测仪器获得的地震动的一致性提供了理想的机会。

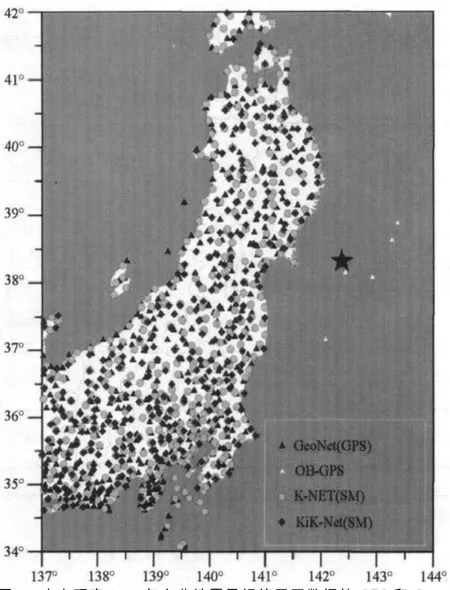
图1 本文研究2011年东北地震最初使用了数据的GPS和Geo－Net、海底GPS／声波台网、K－NET和KiK－Net的强震台站分布图。五角星为美国地质调查局确定的2011年东北地震的震中位置（38.322°N，142.369°E）。本图的彩色版只适用于电子版本

本文首先对估计的位移值的不确定性进行重点评估，从强震数据开始，研究它们对震源反演结果的影响。尤其是，我们提出了一种检测推导数据集中离群值的新方法。这使我们可以在台网分布比日本稀疏时评估两种数据集联合反演是否代表有效选项。我们还对数据覆盖远稀疏于本文实例时检验了我们结果的有效性。最后，我们对高速GPS记录和强震记录得到的位移和速度地震图进行比较，并说明它们在宽频带上如何互补。

1 强震记录与GPS记录获得的静态同震位移比较

为了得到可靠的永久位移估计值，我们首先使用Wang等（2011）提出的自动经验基线校正方法对K－NET和KiK－net这两个台网采集的全部强震数据集进行分析。经验基线校正法基于的概念与最初由Iwan等（1985）提出的相同，其中采用双线性函数描述在强震记录中由基线误差引起的速度趋势。目前，已经描述了几种人工或自动版的方法（见Wang et al，2011及其内的参考文献）。它们之间唯一的差别在于双线性校正两个时间参数的选择。在Wang等（2011）的方法中，时间参数确定的方式确保了校正的位移时程最拟合阶梯函数。基线校正后，通过时间上的积分，获得速度和位移地震图。永久位移通常也称为同震位移，从校正过的位移时程的事件后平稳估计出。尽管后者在这个过程中可能未被充分体现，但正如下文所述，强震数据可提供有关初始形变的重要信息。

图1为研究区内GeoNet、K－NET和KiK－Net台站的位置图。同震位移是分别由K－NET、KiK－Net－SF（地表传感器）和 KiKNet－BH（井下传感器）获得的，并在图2给出，其中画出高精度的GPS解作为参考。一般来说，KiK－Net－BH数据集获得的位移值最稳定（具有相干空间可变性），也与GPS观测结果最接近。其位移矢量集中指向震源矩心（如后面所述）。GPS观测站和KiK－Net台站都在仙台附近海岸观测到约5m的最大位移。K－NET数据集显示出位移空间变化很大，也在相互靠近的两个台站之间。实际上，由于K－NET被设计的是主要为了快速响应，其台站大都布设在公共办公场所、学校、公园和比KiK－Net台站更松软的沉积物自由面上（Tsuda et al，2006；Aoi et al，2011）。可能这些台站下方松软的土质会放大响应，从而使加速度仪产生大的瞬态倾斜（Graizer 2005，2010）。因此，由K－NET数据得到的同震位移本文将不再作进一步的讨论。KiK－NeT有几台地表传感器也观测到一些孤立的异常位移值，与邻近台站测得的位移值不相干。这种异常的一个 例 子 由 KiK－Net的 FKSH18台 站（37.4894°N，140.5380°E）的传感器给出，甚至显示出东西向的位移也与恢复的总体趋势不符（图3）。我们推测认为，这种异常现象的产生主要是因为非线性基线偏移影响了强震记录，采用双线性校正方法并不能适当地计及这种情况。理论上讲，地面倾斜对垂直分量的影响不大。本文实例也验证了这一点。从K－NET和KiK－Net数据集导出的垂直位移中未出现极端异常值。

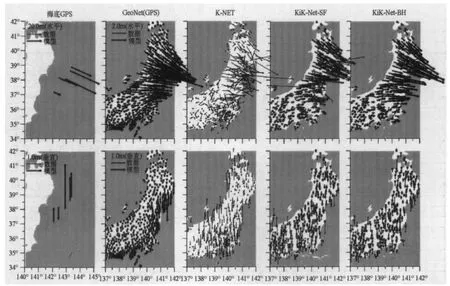
图2 由不同GPS和强震台网观测的2011年东北地震的同震位移数据与由模型1～3（图4）通过相应数据集反演预测的值的比较。因为K－NET存在较大的不确定性，所以未由其得出模型。海岸和近海的GPS数据集的模型均为联合反演的结果。本图的彩色版只适用于电子版本

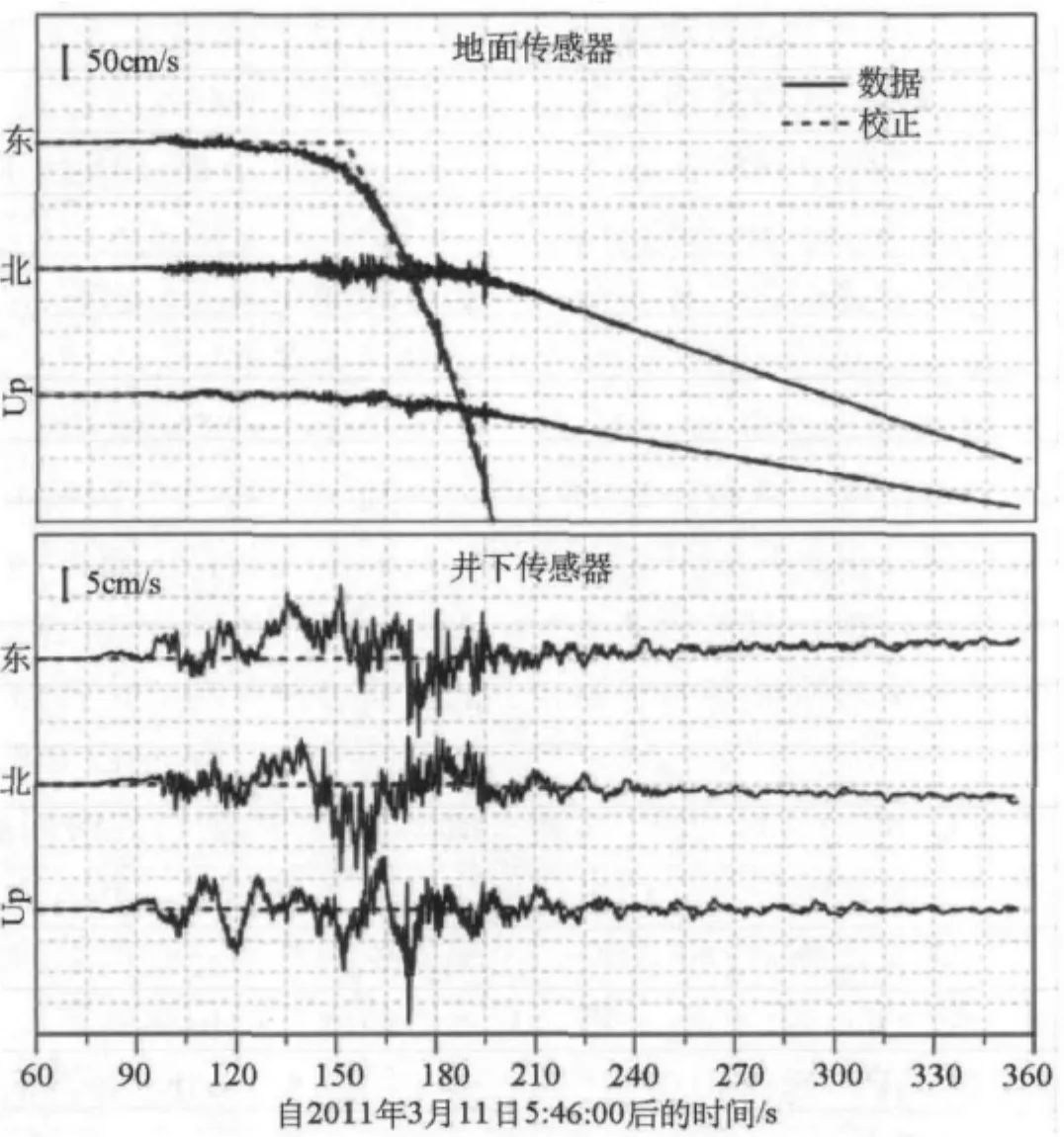
图3 由KiK－Net的FKSH18台站（37.4894°N，140.5380°E）地表和井下加速度仪的记录获得的地面速度。基线校正采用Wang等（2011）的自动经验方法估计。本图的彩色版只适用于电子版本

在下一节比较震源模型之前，我们先对KiK－Net－BH数据得到的与GPS内插的同震位移进行比较。这两种数据集之间偏差位移矢量的均方根为0.47m，相当于KiKNet－BH 绝对位移矢量（1.25m）均方根的37%。因此，假设大的同震位移与MW9.0东北地震有关，这两种数据集就会非常相似，并提供独立的观测点，这可能对下面介绍的震源模型有影响。

2 GPS和强震同震位移数据得到的震源模型间的比较

为了评估强震记录得到的同震位移数据的最大不确定性对震源模拟的影响，我们分别根据KiK－Net的两个数据集反演静态滑动分布，并将反演所获结果与由高精度GPS数据获得的结果进行对比。

反演用自展软件（由R.Wang编写的FORTRAN “SDM”）基于约束最小二乘法进行，已经广泛用于大地测量滑动模型的近期 研 究 中 （Motagh et al，2008，2010；Wang et al，2009，2011；Diao et al，2010，2011；Xu et al，2010）。为了简化数值分析过程，断层面选择由数个滑动均匀的矩形小位错片区组成。观测的位移数据通过地球模型的格林函数与离散的断层滑动相关，并用线弹性位错理论计算。为了使离散的滑动充分代表真实连续的滑动分布，片区的尺度必须合理地小些（Segall and Harris，1987）。事实上，如果得到的数据未包括确定理想分辨率的滑动分布所需要的足够信息，该反演系统则成为欠定系统。为了克服这种欠定系统固有的非唯一性和不稳定性问题，考虑了先验条件（固定断层几何形状并限制滑动角变化范围）和物理约束（滑动的平滑空间分布或应力降。见Du et al，1998）。

本研究中，我们选择一个稍弯曲的断层面，与假设的俯冲板块平行。倾角从顶部（海底）10°线性地增加到约80km深度的20°，这与Pollitz等（2011）提出的情况一致。为了避免任何人为限定因素干扰，选择了足够大的潜在破裂区（约650km×300km）。断层的上边缘位于日本以东的海沟，在太平洋板块与欧亚板块的交界处。片区的尺度约为10km×10km。确定每个断层片区滑动方向的滑动角可在90°±20°之间变化，相当于远震震源机制解的不确定性上限。基于多层弹性半空间模型计算格林函数（Wang， Lorenzo－Martin， Roth，2003；Wang et al，2006）。从CRUST2.0模型数据库（Bassin et al，2000）中选择模型参数。平滑项的加权因子（也称平滑因子）首先考虑满足全部GPS数据的反演进行优化，包括采自Sato等（2011）的近海观测数据，然后对全部其他反演进行固定。

反演结果如图4所示。由于所用台网的台站密度高，我们假设结果的差异是由于反演所用数据的质量不同所致。分辨最好的滑动模型假设为由高精度GPS数据得到的模型，包括海岸和近海的观测数据。实际上，该模型显示的地震峰值同震滑动达到约50m，与此前由Simons等（2011）通过联合反演岸上GPS和深海海啸数据得到的结果一致，但是却比Pollitz等（2011）得到的33m滑动峰值大，后者也同样采用海岸和近海的GPS数据，只是断层几何稍有不同（三个连接的矩形体），通过解析埃尔米特—高斯函数近似滑动分布。其他一些近年来发布的仅根据岸上GPS数据反演的滑动模型，其滑动峰值均低于35m（如，Iinuma et al，2011；Ozawa et al，2011），而根据远震波形数据的滑动模型显示出有大的散射，介于30m与60m之间（如，Ammon et al，2011；Lay et al，2011）。计算出的矩震级为8.90，与全球地震台网GEOFON给出的值相吻合。需要注意的是，在计算地震矩时，我们采用通用的恒定剪切模量μo＝30GPa，代替由地球模型给出的取决于深度的剪切模量。如果采用后者，得出的矩震级将达到9.01。选择恒定剪切模量的原因，是我们想要根据滑移量（而不是地震矩）来比较不同的滑动模型。因此这里所用的剪切模量只起标度因子的作用。

用最好的大地测量滑动模型作为参考，由KiK－Net－BH数据集导出的模型3（见图4）非常令人满意，并可认为优于由KiKNet－SF数据集导出的模型（图4模型2），后者大大低估了地震的震级。值得注意的是，50m的滑动峰值只有在使用海底GPS数据时才能获得。没有这种数据，由GPS导出的滑动模型（模型4）与KiK－Net－BH数据集得到的模型（模型3）近乎相同，二者波形相似，滑动峰值均小于25m。模型3与岸上GPS数据的拟合与模型1的拟合同等好。

3 检测强震所得同震位移离群值的基于模型的方法

在上两节中我们指出，与先前其他地方的研究一致，2011年日本东北地震期间的大同震位移也可使用经验基线校正工具由强震记录可靠地恢复。虽然在个别台站获得的位移值会有较大的不确定性，然而，只要传感器安装在井下或至少安装在硬质地面上，考虑整个密集的台网时仍能得到稳健的震源机制解。实际上，这种理想的安装条件并非总能满足，不但由于经费和后勤方面的限制，而且因为许多强震台站为了工程目的而有意安装在松软沉积层上和城区内。因此，很可能由放大效应和瞬时倾斜效应产生大的基线误差，而且采用经验双线性校正法也很难充分加以校正。结果是，在强震得到的位移数据中就出现了明显的离群值（见图2）。因为这些离群值可能会影响滑动反演的结果，我们提出了一种基于模型的方法对这些离群值进行检测。

例如，我们首先对全部的KiK－Net－SF数据集进行反演，得到初步的滑动模型。在输入的数据集中如果某一观测的地表位移值与预测值失配超过一定阈值则定为离群值。作为例子，图5显示了去除与模型偏差超过15°的离群值矢量后的KiK－Net两个数据集。这里选择15°作为方向阀值，使得滤波后的KiK－Net－SF数据仍然表现出空间变化的合理相干性。我们没有根据矢量幅度对离群位移值滤波，因为它对约束震源定位影响不大。对离群值滤波后，与GPS数据相比，KiK－Net－BH数据集的统计偏差由之前的37%降至20%。

一线教师的付出是辛劳的，不仅仅是脑力劳动，同时还有体力劳动，费心费力。备课、上课、批改作业和试卷，还要反思教学，针对个别学生补缺补差，很少有休息时间。可是，作为一名教师，只有用心教学才能赢得家长的尊重和理解，在工作中，只有家长和学校相互配合，教师和家长之间互相理解和尊重，才能共同的把孩子教育好。应该说，我们需要家长的配合，理解和支持，让学生学好是共同的期待，这需要我们用心与家长沟通、交流，做家长的朋友。得到了家长的理解和支持，我们才能教出成绩，从而收获快乐，提升幸福感。

在台站密集的地区，通过相邻台站之间的对比也很容易发现离群值，但这种基于模型的检测方法也可用于台网分布不均匀的地区。值得注意的是，使用滤波后的数据时，我们可显著地改善滑动模型，特别是用KiK－Net－SF数据集反演的矩震级（图4模型5）。由于振幅相对小，大多数垂直分量都处于该方法的偏差范围之内。

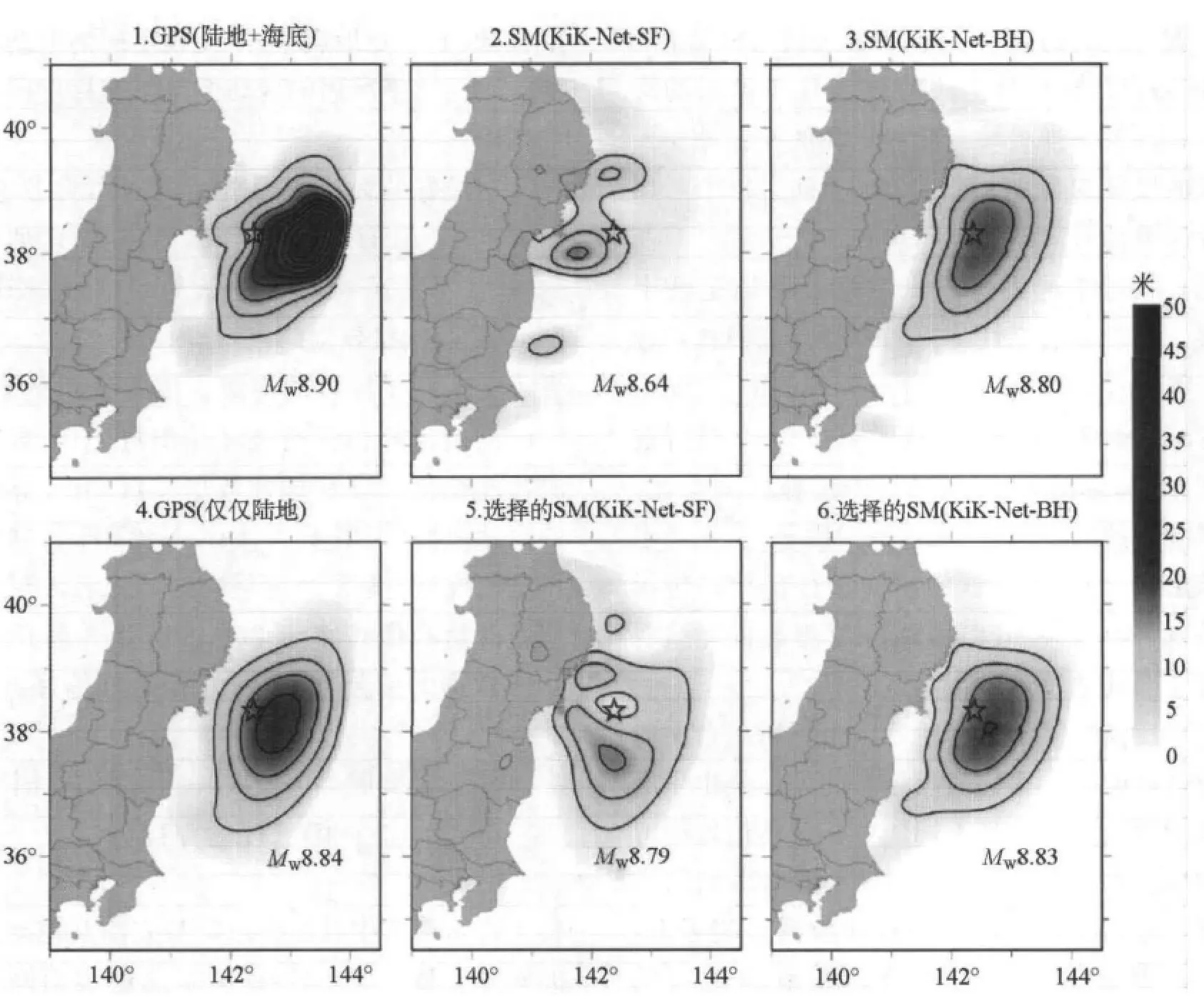
图4 由不同同震位移数据集反演的滑动模型（OB：海底；SM，强震得到的；SF，地表传感器；BH，井下传感器）。数据在图2给出。选择的KiK－Net地表和井下数据在图5给出。反演使用了水平和垂直两种分量。等值线间距为5m。本图的彩色版只适用于电子版本

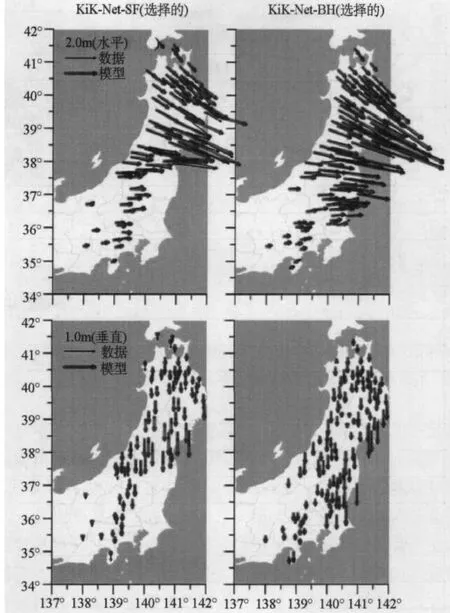
图5 由KiK－Net所选台站的强震记录得到的同震位移数据，其中观测的三维位移矢量与图4中的模型2和模型3分别预测的偏差均小于15°。本图的彩色版只适用于电子版本

在全球的大部分其他地区，不论是大地测量台网还是地震台网的分布一般都比在日本稀疏。因为我们已经说明与GPS直接测量的数据相比，由强震数据得到的位移有可接受的质量，将各个测量系统组合起来就可提高这些地区的数据覆盖，因而可以降低单独使用GPS数据时震源反演的不确定性。为了模拟这种情况，我们做了一个测试，从GPS数据集和 KiK－Net－SF数据集（没有离群值）分别随机选择25个位移矢量。如图6所示，尽管只使用了约10%的原始数据，但可以得到令人满意的震源。我们将这一结果归因于过滤掉离群值后数据的剩余方位角覆盖和数据质量的提高。

4 GPS与强震记录时间序列的比较

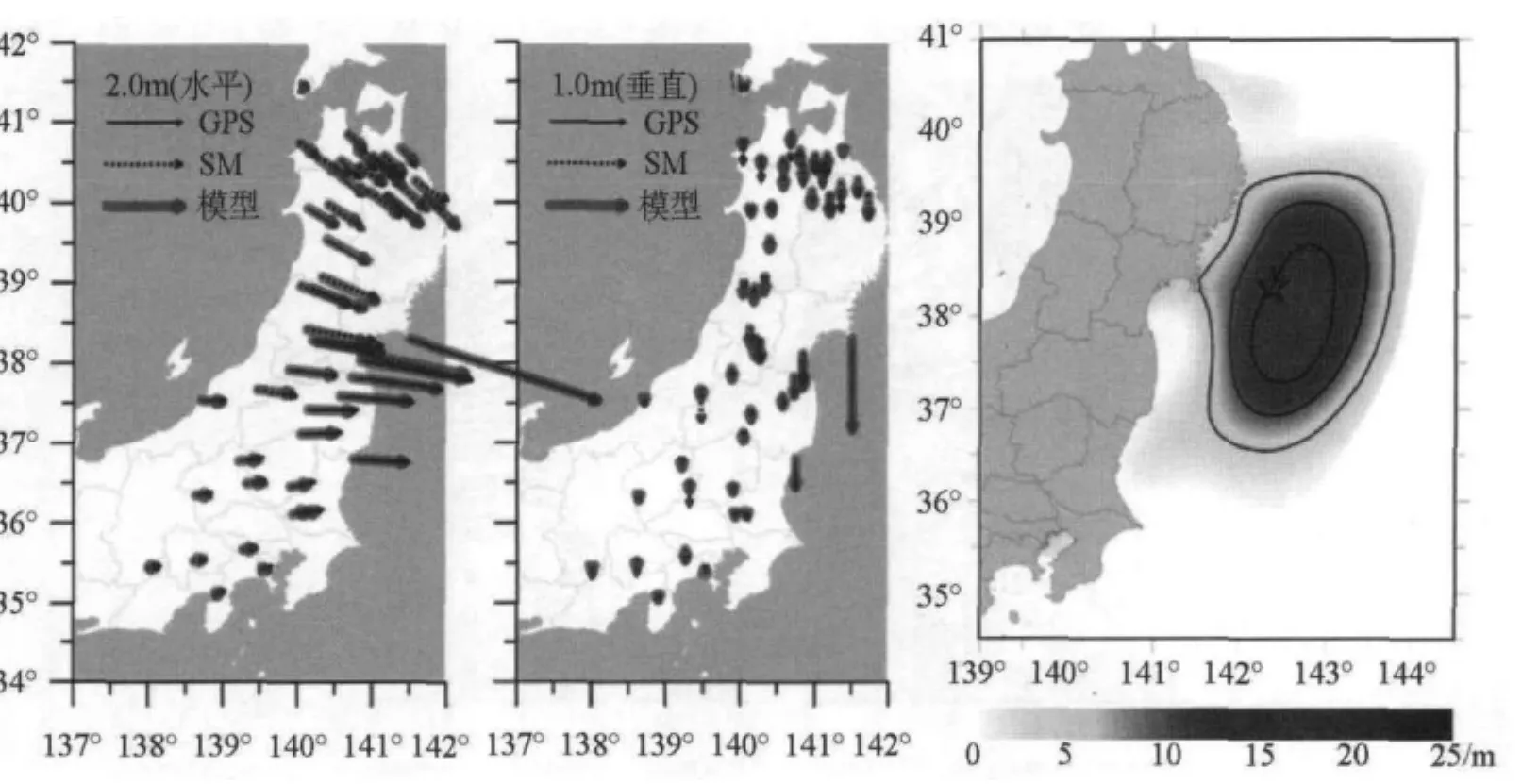
图6 从GPS和KiK－Net－SF数据集随机选择的同震位移数据（图2）以及由联合反演得到的相关滑动模型。本图的彩色版只适用于电子版本

高速GPS和强震台网的另一个重要用途是提供近场地震波形数据，而这种数据对约束运动学震源过程有用。实际上，低频带的波形信息对反演震源时间函数特别有用。因此，我们需要通过强震记录得到速度或位移地震图，这对经验基线校正方法也是必要的。不进行基线校正，就需要对强震记录进行高通或者带通滤波，从而导致低频和静态地面形变信息的丢失，而这些信息对估计矩震级非常重要。

强震得到的速度或位移地震图的不确定性可用同时安装的高速GPS作为参照得到最好的评估。尽管日本有全球最密集的GPS和强震台网，但将两种仪器同时安装的台站却很少。尽管如此，我们还是发现12对以上同时安装（近似配置）GeoNet和KiK－Net台站的台站对。采用由 Wang等（2011）提出的自动基线校正方法，我们从强震记录得到了速度和位移地震图，并将它们与全部14对间距≤4km的台站对的GPS数据进行比较（图7）。只有少数案例中的强震位移地震图与高速GPS数据相差较大，大多数在永久位移到达之后的周期内。KiK－Net的FKSH07台站井下传感器结果最差（图7中的14号），其中东西向位移收敛于GPS相反的最终值。此情况的部分原因是，强震记录不允许我们选择足够的事件前和事件后的时间，而这对使用自动方法进行成功经验基线校正是必要的。然而，在所有其他情况下，由高速GPS和强震记录得出的速度地震图令人满意地彼此一致，佐证了前面的观测结果，即经验基线校正的不确定性可对得到的速度地震图有影响，但没有对位移地震图的影响那样大（Boore，2001）。

5 高速GPS记录和强震记录的联合使用

在先前探讨其他大地震，如1999年集集（中国台湾）、2007年托科皮亚（智利）和2008年汶川（中国）地震的研究中（Wu and Wu，2007；Wang et al，2011），固定台站的高速GPS数据不能得到，但根据临时GPS台网或InSAR观测记录，很好估计出了强震台站的静态同震位移。因此，将已知的同震位移作为参考，研究经验基线校正是否能够得到改进是令人感兴趣的。我们建议对选择时间参数的判据做修定，以便最终的位移与GPS参考值最接近。我们的结果表明，使用GPS参考值可明显改善由强震记录恢复位移过程（图8），为研究地震破裂过程提供更精确的有用低频波形数据。

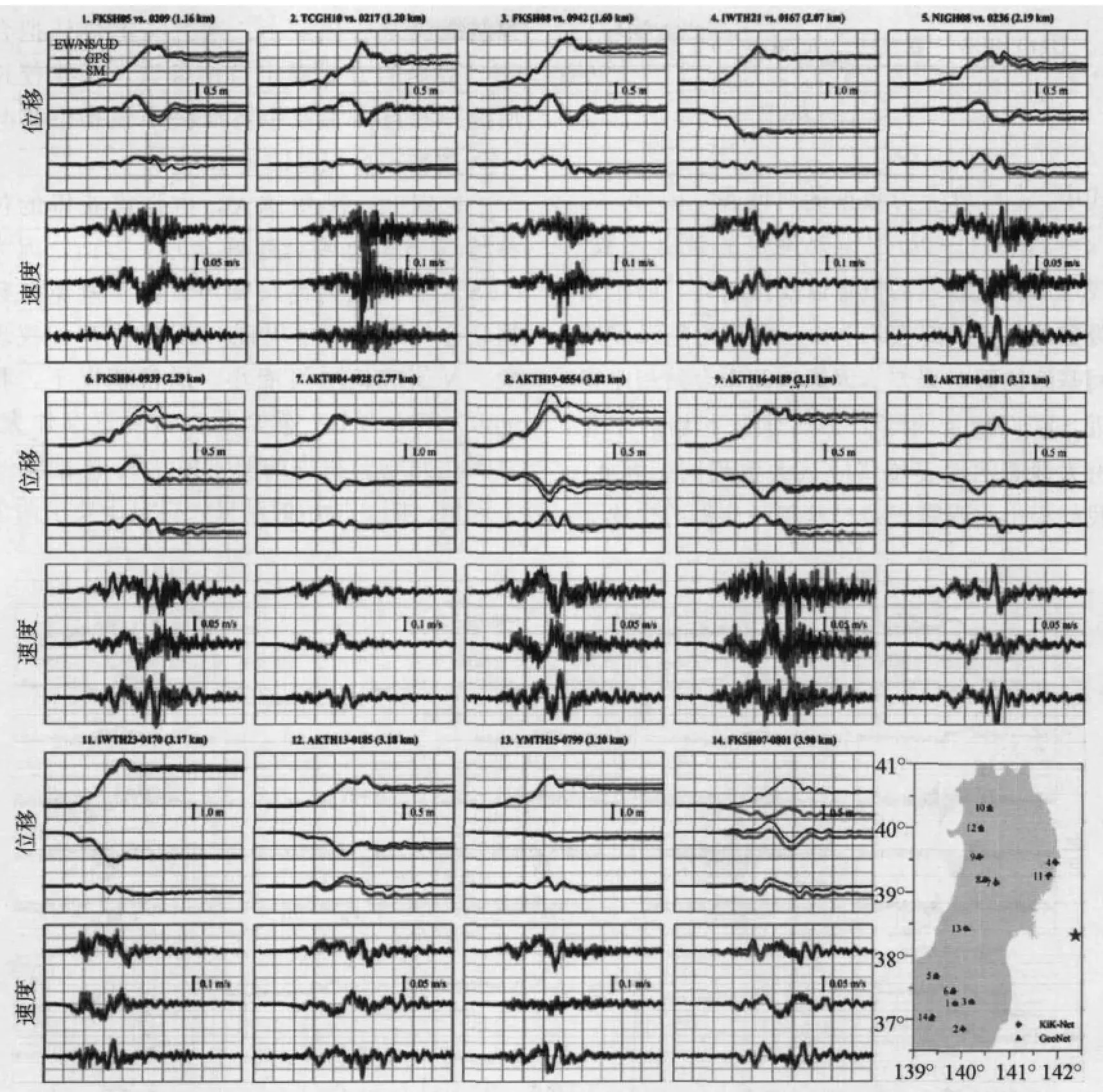
图7 采用Wang等（2011）的自动基线校正工具从KiK－Net井下台站强震记录得到的2011年东北地震的位移地震图和速度地震图与相邻GPS观测图的对比。台站对的编号与台站分布图中的编号相对应。时间窗一律为250s。本图的彩色版只适用于电子版本

对于近同时安装的GPS和强震台站，通过联合使用两种仪器可以得到宽频带的真实地震动信息。作为例子，我们选择了强震台网与GPS台网之间相距最近的台站对，即 K－NET 的台站 AKT006（40.2152°N，140.7873°E）和 GeoNet 的 台 站 0183（40.2154°N，140.7873°E）， 二 者 相 距20m。图9清晰地显示出了两种观测方法出现的问题。地面倾斜致使由强震记录二重积分得到的水平位移分量有大的误差趋势，而GPS位移进行二重求导后，地面加速度被大大低估。由于GPS采样率低（1Hz），二重差分之后高频成分丢失了，而且还可能会出现混淆效应。下面我们提出联合使用GPS和强震记录的简单方法。

我们首先从GPS数据中去除事件前的偏移。然后我们假设加速度仪每个分量的基线误差是时间的函数，并一般可用线性函数结合正弦函数表示：

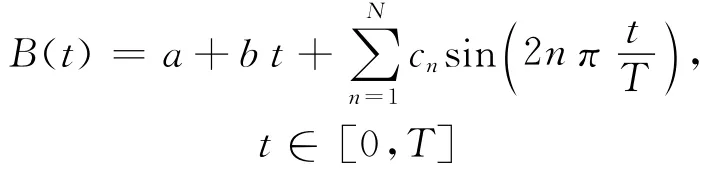
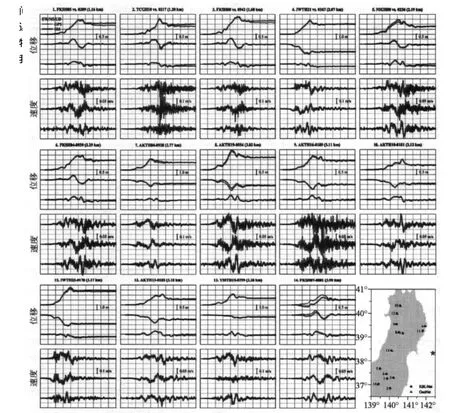
图8 同图7，只是在强震记录的基线校正过程中用GPS永久位移作为参考。本图的彩色版只适用于电子版本

原则上，N值越大，由强震获得的位移与GPS数据吻合越好。另一方面，因为GPS含有较大的高频噪声，为了避免在数据联合处理过程中出现GPS数据超加权现象，N值应该尽可能小。通常情况下，我们以N＝0开始，然后根据需要逐渐加大，直到达到吻合程度的要求或达到N的某一上限值。图9所示的结果，得自于要求两个水平分量的拟合误差不大于±1cm，垂直分量不大于±2cm，基本与GPS的测量误差相符合。得到的结果是N值在东、北和垂直分量分别为5、8和0。尽管基线校正所用的函数（图9c右上图的灰色粗曲线）非常平滑，但基于强震的位移与GPS数据（图9c右下图的灰色粗曲线）之间的不吻合可能与高频地震信号无关。因此，这些不吻合可能是由强震和GPS两种数据中的随机观测噪声引起的，但也不排除两种观测设备安装条件差异的影响。图9也给出了联合使用GPS和强震数据所恢复的地面速度（右边中间图），为获取宽频带地震数据打下了基础。在此基础上，人们就可以通过积分获得地面位移（右下图），通过微分获得地面加速度（右上图），两者的分辨率比单独采用大地测量和地震观测得出的结果要高许多。

6 讨论与结论

日本具有世界上最密集的大地测量和地震台网。一旦发生大地震，就可通过这些台网近实时地获得地震动的信息。采用自动经验基线校正方法，我们对K－NET和KiKNet强震台网记录的2011年东北地震的加速度图进行了分析。由KiK－Net井下数据集得到的同震位移与高精度GPS解最接近。相比之下，KiK－Net的地表台站数据集显示出较大的不确定性，但就其整个台网数据而言，其结果还是稳健的。由K－NET数据集得到的同震位移结果置信度较差，表现出大的空间可变性。可能强放大土壤响应，包括地表倾斜（Bonilla et al，2011），导致大部分K－NET传感器以及一些KiK－Net的地表传感器出现了复杂、多重的基线漂移，使得简单的双线性校正方法未能有效。

我们分别用KiK－Net的两个数据集反演了静态滑动分布，并将其与高精度GPS数据获得的结果作了对比。当选择常用的恒定剪切模量μo＝30GPa将滑动转换成地震矩时，根据强震或由GPS同震位移场得到的该地震的矩震级大约为8.8到8.9，稍小于美国地质调查局（USGS）提供的最终矩心矩张量解9.0，但与GEOFON台网的值一致。目前，由近场大地测量数据反演得到的滑动模型多数都基于均匀弹性半空间，其主要原因是可以用闭解析式计算格林函数。众所周知，在均匀弹性半空间由位错源引起的静态位移取决于泊松比，但与介质的剪切模量绝对值无关。这可能对层状结构无效，而忽略这一点可能会造成地表静态位移高达20%的误差（Pollitz，1996）。此外，最新的研究表明，当反演基于的模型结合了随深度而变的剪切模量时，得到的地震矩由于震源位置较深而比基于均匀半空间模型得到的可能 会 高 出 40% （Hearn and Bürgmann，2005）。因此，为了独立地确定矩震级，在反演大地测量数据时应考虑分层地壳构造的影响。我们注意到，复杂的断层几何形状可能对数据的解释有影响。

基线误差通过经验校正后，通过时间积分，从强震记录得出了地面速度和位移时程。一般情况下，由KiK－Net数据反演得到的滑动模型结果与由高速GPS观测所得结果的吻合效果，比由K－NET数据得到的结果吻合效果好。K－NET数据似乎受场地效应影响很大（记录中的强非线性趋势，应该归咎于布设在松软地面上传感器的瞬时较大倾斜），因此在找到有效的方法对这种效应加以校正之前不可使用。由KiK－Net井下记录得到的速度时程几乎不受经过经验基线校正后仍然存在的残余不确定性的影响，并且由于其较高的采样率（100Hz），可以提供比1Hz的GPS数据更多用速度乃至能量表征地震动的信息。

地震动数据覆盖的频带越宽越好，以满足地球物理及工程研究等各方面的需要。为了验证考虑强震和GPS数据时情况是否如此，我们对数据集在地面形变信息不同频带占优势的加速度、速度和位移域进行了对比。一方面，我们对KiK－Net－BH强震记录经过经验基线校正后进行积分，获得速度和位移地震图。另一方面，我们对高速GPS时间序列进行微分以获得速度地震图，但不导出加速度地震图，这是因为1Hz的GPS采样率较低，只能与低通滤波的加速度图进行对比。尽管在理论上目前GPS接收器的最高采样率可达50Hz，然而预计由此获得的加速度可能会有很强的噪声，而且不能有任何实际把握用来替代强震记录。

我们也试图对由 Wang（2011）提出的强震记录基线校正是否在用GPS同震位移作为参考时可得到改善进行了评估和验证。我们得出的结果在分别由GPS和强震数据估计的速度和位移时程的互换性方面是成功的。此外，我们还说明了一个例子，其中将来自同时安装两种仪器测点的高速GPS和强震数据进行组合来恢复宽频带（0～100Hz）的地震动信息。预计将来同时安装高速GPS和强震仪的台站会越来越多，联合使用这两种数据进行处理将有助于近实时反演运动学震源过程，因而会对地震和海啸的早期预警具有重大影响。

数据与来源

K－NET和KiK－net强震数据由日本国家地球科学与防灾研究所（NIED）提供并分别从 http：／／www.k－net.bosai.go.jp／和http：／／www.kik.bosai.go.jp／（最后访问时间2011年6月）得到。所有原始GeoNet GPS数据由地球空间信息管理局（GSI）提供。GPS同震位移数据由喷气推进实验室和加州理工学院的ARIA团队得到，下载自ftp：／／sideshow.jpl.nasa.gov／pub／usrs／ARIA／（最后访问时间2011年3月）。1Hz GPS数据（地球空间信息管理局所有，经由日本GPS数据服务公司得到）下载自http：／／rtgps.com／rtnet＿dl＿eq.php（最后访问时间2011年4月）。2011年东北地震的远震 震 源 机 制 解 选 自：http：／／geofon.gfzpotsdam.de／data／alerts／2011／gfz2011ewla／mt.txt（最后访问时间2011年3月）。CRUST2.0模型下载自http：／／igppweb.ucsd.edu／～gabi／crust2.html（最后访问时间2011年3）。