断层阶跃对地震动的影响

J.C.Lozos D.D.Oglesby J.N.Brune

引言

真实的断层很少有完全光滑的平面特征。无论断层滑动面形貌的规模还是整个标绘的断层迹线的尺度，几何复杂性才是多数断层的实际特征。由于弯曲、分支和阶跃在自然界中普遍存在，因此考虑这些断层的特征对破裂扩展进而对地震动的影响，对风险评估及更好地了解地震过程极其重要。本研究特别重点研究两个不相连阶跃的情况——走滑断层中两个相隔一定距离的平行的断层段和它们是如何影响地震动的分布和强度的。

几何复杂性对地震的许多方面产生影响：破裂速度、滑动速率、滑动总体分布以及破裂从一个断层线开始又从另一个断层线启动的情况下，破裂在第一段停止和在第二段开始之间的时间。这些因素影响着真实地震的地震动分布和强度；Wald和Heaton（1994）对破裂几何形状非常复杂的1992年加利福尼亚兰德斯地震描述了这些影响。当地和区域强震传感器记录显示，兰德斯地区非均匀的滑动、滑动速率和破裂速度导致了断层面周围强震动的不规则分布。Brune（2002）提出了另一种意见，认为几何复杂性可通过这些复杂性改变与破裂有关的地震动的分布。他发现，在圣哈辛托和埃尔西诺断层的重叠段附近有几组不稳定平衡的岩体，这可能说明，通过重叠区本身的破裂可能产生比平面断层上连续破裂预期的更低的地震动。这些例子突显了系统研究破裂通过几何不连续性对地震动影响的重要性，而作者认为本研究便是其第一个例子。

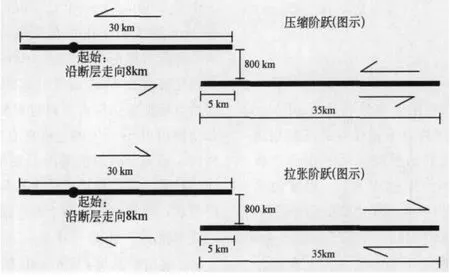
图1 断层几何图。黑线代表两个平行的断层段，长度固定。所有模型中两个断层段之间的起始点和重叠量也固定。两断层段间的间距是唯一的几何变量。阶跃是压缩的还是拉张的由断层系上的剪切方向确定

关于阶跃是如何影响地震破裂过程的已进行了一些研究（例如，Harris et al，1991；Harris and Day，1993；Kase and Kuge，1998，2001；Oglesby et al，2003；Duan and Oglesby，2006；Oglesby，2008；Lozos et al，2011）。这些模式地震显示了与实际观测相同类型的几何形状引起的属性：破裂速度的不均匀性、滑动速率和滑动的总体分布。它们还表明，破裂之所以能重新在第二断层段发生是由于破裂扩展到第一个破裂段末端时能量释放停止期导致的；这一通过期被认为足以将第二段的剪切应力提高至破裂点。因此，不管两个破裂段之间有多少重叠，破裂很少在第二段上形成，除非它到达第一段的末端（Duan and Oglesby，2006）。Harris等（1991）以及 Harris和 Day（1993）的研究对本研究特别重要。这些研究使用了几种不同区域应力状态下走滑断层中不相连阶跃的动态模型来确定允许破裂在第二断层段再次起始的阶跃的最大宽度。他们发现，在他们特定的物理和计算参数中，最宽可跳跃的阶跃是拉张情况下两个断层段之间相隔5km；破裂跨越如此宽的阶跃，要求断层系非常接近破裂点，导致超剪切破裂速度。为了延续以往的研究并进行对比，我们用这些研究中的许多参数作为我们自己研究的开始点。

现实中的断层也很少存在于完全均质的材料背景中。已有许多为调查材料性质和界面对破裂扩展影响的模拟研究（例如，Andrews and Ben Zion，1997；Harris and Day，1997；Cochard and Rice，2000；Shi and Ben Zion，2006；Ma and Beroza，2008；Dalguer and Day，2009）。然而，这些研究都集中在平面断层，没有扩大范围讨论地震动。

1 方法

1.1 计算方法

我们用三维有限元方法软件FaultMod（Barall，2009）对具有不相连阶跃的断层进行动态模拟。我们的模型采用了库仑摩擦（t≤μσn，其中t为摩擦应力，μ为摩擦系数，σn为正应力）和滑动弱化摩擦定律（Ida，1972；Palmer and Rice，1973；Andrews，1976）。将所有断层的临界滑动弱化距离定为0.4m的恒定值。

为了确保模型在计算上的可行性，使用的单元尺寸为200m。使用这一离散化，模型并没有分辨现实情况中对破坏性地震动有作用的高频信号。我们模拟的最大频率在固体花岗岩中为1.29Hz，材料越松软值越低；已知对结构极具破坏性的频率属于1～10Hz之列。我们以100m离散化进行了一些初步的模拟，以证实我们较好地判定滑动弱化参数；我们甚至在最慢的材料背景中该离散尺寸之间也没看到破裂行为和最终的地震动分布有任何差异，证明我们的结果对网格没有依赖性。使用100m的单元尺寸仍未产生足够高频的地震动以获得整个破坏性频率范围，所以为了计算效率我们选用了200m的单元尺寸，这就允许我们进行更多的模拟。本研究的重点是对具有不相连阶跃的走滑断层上与破裂有关的地震动的分布和模式进行定性描述。较之其他断层而言，这种走滑断层的几何形状和破裂速度能够产生更多或更少的地震动。为了准确模拟这些更高频的运动——从工程的角度来看，它们对结构具有较大的破坏性——我们需要使用动态模型的滑动分布进行更多数值上有效的运动学模拟。我们正在为未来的研究开发这种方法。

如图1所示，本研究中所有模型采用的断层都有简化的阶跃几何形状。该系统由两个平行的垂直地面破裂的走滑断层段组成，一个长30km，另一个长35km，两者之间有5km的重叠，在垂直于走向间距不同。这两个断层段的深度均为16km。通过人工干预使破裂在8km深度处起始，方法是在起始点施加剪切应力至超过屈服应力10%，并使破裂以3km／s的速度在直径为6km的片区，即大于破裂扩展所需要的临界尺度，向外扩展。我们模拟了拉张和压缩这两种几何形状；这通过改变两个断层段上剪切应力的符号完成。作为对比点，我们也模拟了30km（起始段长度）和60km（整个阶跃断层系的长度）的平面断层。

1.2 阶跃宽度、应力降和获得的破裂速度

为了检查断层段之间间距对地震动分布的影响，我们选用基于Harris和Day（1993；以下简称HD93）相关研究的断层间距、区域应力组态和破裂速度模拟阶跃。他们使用了应力状态下1，2，3和4km的断层间距，使得破裂速度低于剪切波的传播速度（亚剪切）也高于剪切波的传播速度（超剪切）。所施加的应力状态直接影响破裂速度；应力越接近破裂点，断层就越容易继续再次破裂，这就产生能够通过更宽几何间断区扩展的更高能、更快速的破裂前沿。我们模型中的应力状态也是基于HD93中的这些因素。HD93亚剪切情况下的应力产生3MPa的应力降，该应力降在我们的模型中不能使破裂跳跃到第二断层段。因为我们更想看到通过阶跃的扩展对地震动的影响，而不是阶跃的宽度对破裂的延滞，我们将HD93应力增加一倍，产生的应力降为6MPa，以保证破裂扩展。HD93的超剪切情况应力降为10MPa，比推断的平均走滑地震的应力降高。我们取用了这些应力并将它们降低到其初始值的60%以产生6MPa的应力降，这与我们亚剪切情况下的应力降一致，也更属于走滑型地震推断的应力降范围之列。表1列出了本研究中使用的应力组态。

表1 应力情况

表2 模型材料性质

与HD93类似，我们在断层段之间选择间距为1，2，3和4km的模拟阶跃。当使用超剪切破裂速度应力设置时，破裂通过所有这些宽度扩展，反射它们的结果。然而，我们的初步模型表明，亚剪切破裂没有跳跃到阶跃大于1km的第二断层段。因此在亚剪切情况下我们用间隔600m、800m和1 000m模拟阶跃。我们的网格尺寸太大了而不能有效地模拟小于600m的阶跃。

本节中所有的模型均假设断层是嵌于均匀的花岗岩中。表2列出了所用材料的性质。

1.3 材料对比

由于很少有断层在完全均质的岩石中存在，我们选择在几种合理的现实材质位置模拟阶跃系统，并观察材料、界面和阶跃之间的相互作用对地震动分布的影响。以下对这些情况做更详细的描述，并在表2给出所有模型材料的物理性质。

丁小强上了车，看了杜一朵一眼，说一朵啊，你看好了，别让你叔叔缴公粮，要缴也要让他回家缴。杜一朵也喝了不少，乜斜了丁小强一眼，主席的酒肠子长着呢，一时半会缴不了。丁小强系安全带的时候看见了什么，他说，老杜，你的手哪里不好放？要放在美女的大腿上。老杜嘟哝一句说，今天不放，以后哪还有我的机会。身子故意一软斜刺里歪倒下去，丁小强惊呼，小心他吐。

第一种材料变化情况模拟拉张阶跃中充填软沉积物的拉分盆地。这类盆地的深度受周围断层上滑动量的控制，所以我们模拟了两种不同端元深度的情况。可以分辨的最浅的盆地确定的单元尺寸大约为600m。较深的情况为2km，是由圣哈辛托断层的克莱尔蒙特和卡萨洛马段之间的大拉张盆地产生的（Langenheimet al，2004）。图2显示了该模型的几何形状。

接下来的情况是超过一半的空间层模型，在以花岗岩为基底的砂岩层跨越整个模型区域。我们模拟了1km和5km两种不同厚度的砂岩层。更深的情况由洛杉矶盆地产生，尽管实际的盆地在一些地方甚至延伸得更深（Komatitsch et al，2004）。该模型的几何形状如图3所示。

最后一种物质变化情况引入了断层周围的破坏区。尽管断层在该区的几何形状可能很复杂，但为了简单起见，我们使用了一个矩形框，在断层带周围蔓延1km并延伸到该断层系的全部孕震深度。破坏区的密度与围岩花岗岩的密度相等，但波速在破坏的材料中减少了17%，与Harris和Day（1997）关于破坏区如何影响破裂扩展行为的研究相同。该模型几何形状在图4中给出。

我们对所有不同材料的这些模型选用亚剪切破裂速度和800m的断层段间距。虽然超剪切破裂可以跳跃更宽的阶跃，但实际地震观测表明持续的超剪切破裂是极其罕见的。由于需要从现实的材料对比方案确定地震动，我们对该研究部分选择了最可能和最现实的应力状态。

2 结果

2.1 平面断层

60km长的平面断层较拉张和压缩阶跃具有更高的地震动峰值和更宽的高地震动分布。亚剪切和超剪切破裂情况下也如此。60km平面断层的地震动峰值比30km平面断层的高。相比之下，30km的平面断层与相同应力范围内任何阶跃情况下的地震动峰值相同，不论其阶跃宽度多大或其是拉张的还是压缩的。平面断层地震动模式如图5所示。除非另有说明，图5和本文中其他图的比色刻度尺均设置为特定应力情况下均匀花岗岩中阶跃模型得到的地震动峰值。这种比色刻度尺的一致性有利于对比不同模型的结果。

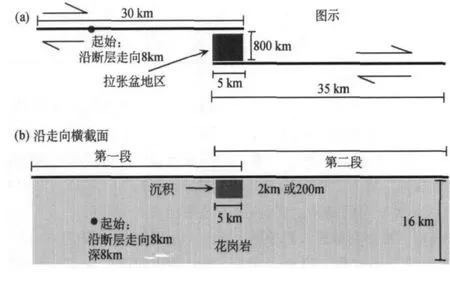
图2 断层之间区域有沉积盆地的拉张阶跃图（不按比例）。（a）模型图示，（b）沿整个断层系走向的横截面。这种几何形状意在模拟拉张沉积盆地。除了盆地的深度，这个几何体的所有其他方面在各个模型中都固定不变

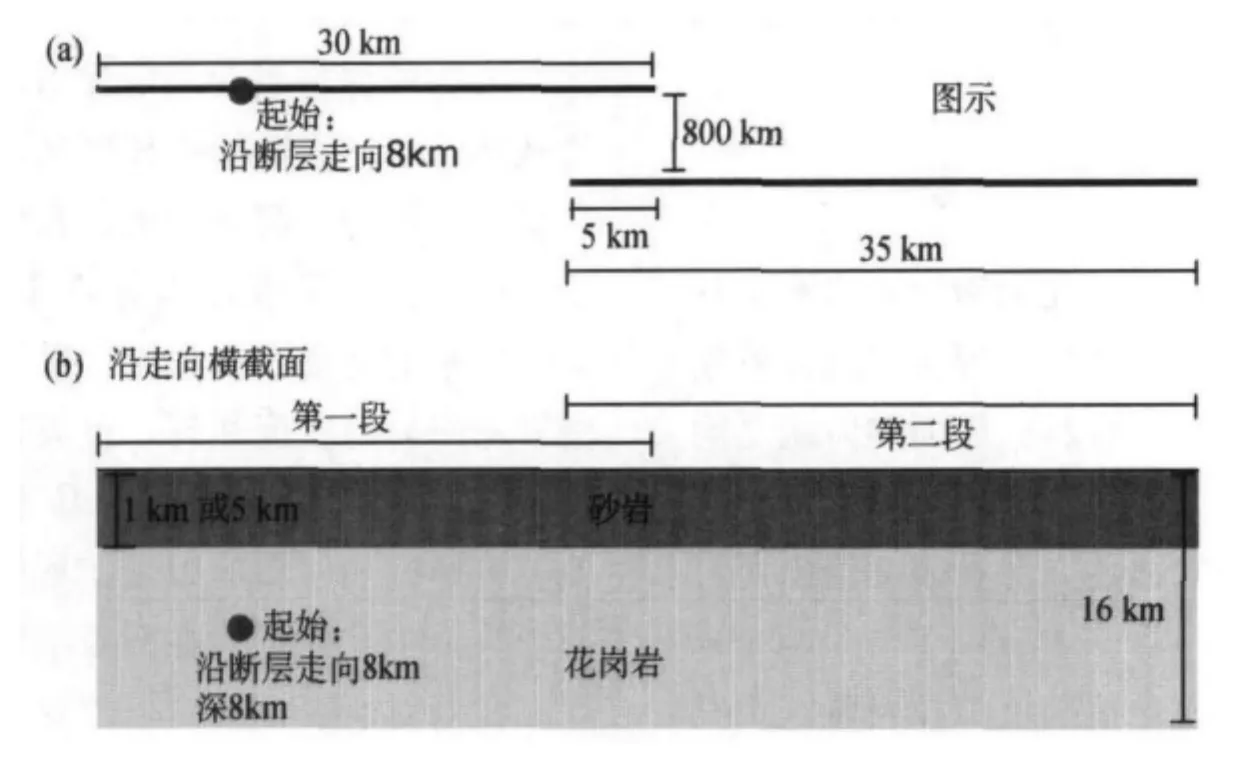
图3 嵌入花岗岩基底上面砂岩层中的断层模型几何图。（a）模型的图示，（b）沿整个断层系走向的横截面。除了砂岩层的厚度，这个几何体的所有其他方面在各个模型中都固定不变

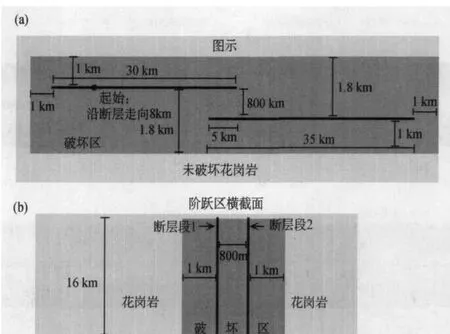
图4 断层周围有破坏区的模型几何图（不按比例）。（a）模型图示，（b）阶跃区横截面

2.2 拉张与压缩阶跃

图6 显示了应力降为6MPa的亚剪切压缩和拉张阶跃模型的地震动图。拉张与压缩情况下地震动的模式相似：地震动减少区正好出现在第一断层段的末端，地震动沿第二断层段的走向增加。在亚剪切情况下，拉张与压缩阶跃具有相同的地震动峰值，两种情况下峰值均发生在起始段，但拉张情况下均出现稍宽的较高地震动分布。在最宽的亚剪切压缩阶跃模型中，断层段间距为1km，破裂根本不会跳跃到第二段。这一结果与早期的研究相一致，表明破裂能够跳过比压缩阶跃更宽的拉张阶跃。

拉张和压缩阶跃间的差异在超剪切应力情况下更加明显。地震动的分布（图7）保持了亚剪切分布的诸多特征：在第一断层段末端地震动减少，沿第二断层段走向地震动增加。地震动峰值在超剪切模型中也发生在起始段。第二断层段地震动分布的变化取决于压缩而非拉张。在拉张阶跃中，在第二段沿走向的稍远处，有一比第一段端点地震动更强的区，但地震动再次下降并占用数千米区域重新建立更广泛的较强运动分布。第二段周围的地震动强度随阶跃的增宽而降低，但沿断层走向的整体模式和位置未发生明显变化。在压缩阶跃中，起始点没有较强震动区，只有沿第二段的走向，从较窄的较低地震动分布扩展到较宽的更高地震动分布。该区域不太对称，沿阶跃内断层的一侧运动较低。更宽的阶跃，在第二段达到最强地震动的点沿第二段断层走向移动到更远的地方。

无论破裂速度如何，阶跃的宽度均不影响任何模型的地震动峰值，这是因为峰值总是发生在第一断层段沿断层走向从起始点长约5km的地方。在所有破裂速度情况下，第二段的运动强度随阶跃宽度的增加而降低。在亚剪切破裂速度模型中，无论段之间的间距如何，拉张阶跃比压缩阶跃在第二断层段始终有更宽的较高运动分布，如图6所示。然而在超剪切情况下，对于1km的间距，压缩阶跃在第二段具有较宽的的较高运动分布，但拉张阶跃在2、3、4km阶跃宽度有更宽的较高运动分布。图7显示了超剪切破裂速度情况下1、2、3、4km宽度的拉张和压缩阶跃的地震动峰值图。阶跃宽度的地震动空间模式变化不明显，与经历较高地震动的拉张情况相对应。

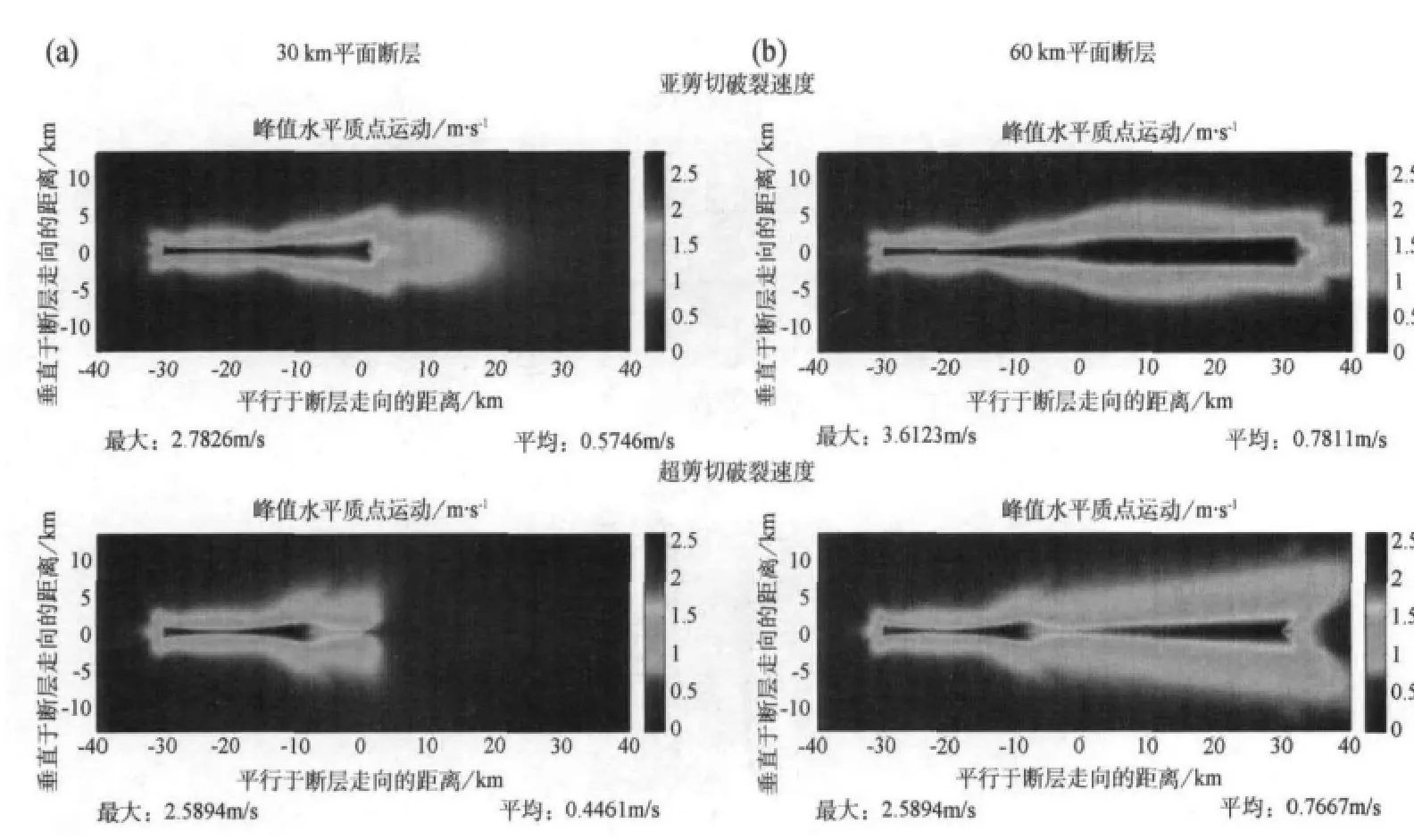
图5 峰值水平质点运动的分布。（a）30km平面断层，（b）60km平面断层。这些断层嵌于均匀花岗岩中，上图为亚剪切破裂速度，下图为超剪切破裂速度。设定这些图的颜色刻度，使得最大值与相应应力情况和介质的阶跃模型产生的最大地震动相对应（如图6）。注意，亚剪切情况下较高运动的分布仍旧比超剪切情况接近断层

2.3 材料对比

将充满沉积物的拉分盆地引入拉张阶跃模型并未显著改变地震动的整体分布，见图8。沉积盆地区域有一个具有极高地震动的局部区域。破裂在第二段起始的较高运动脉冲比在均匀花岗岩情况中更强烈。然而，总的来说，远离断层系与均匀情况下地震动的强度和分布差异可以忽略不计。

与花岗岩基底上面砂岩层有关的地震动的分布和强度对砂岩层的厚度有强烈的依赖性。图9比较了薄厚砂岩层情况下地震动的分布。对于1km的砂岩层，拉张和压缩阶跃之间在运动强度和模式上的差异可忽略不计。这里的模式不同于均匀花岗岩情况下，其中在第二段上的运动增加，又略有下降，随后沿断层走向再次增加，而不是仅仅沿断层走向在强度和分布宽度上增加。然而，对于5km厚的砂岩层，压缩情况显示出了与拉张情况截然不同的模式，拉张情况仍然有与1km沉积层模式类似的模式。5km层的压缩模型有地震动较高的广阔地区，始于沿断层走向约15km处，不同于拉张（或1km层）情况下高地震动的渐缓蔓延。

在断层系周围引入破坏区，提高了整个断层系的地震动峰值。与均匀花岗岩相比，破坏区也改变了两个断层段附近地震动的分布。这种模式如图10所示。随着破裂前沿扩展得离强制起始区更远，起始段运动的强度降低，而在花岗岩情况下该强度是增加、降低，随后再次增加。尽管断层周围运动的整体模式更对称，在拉张和压缩这两种情况下第二段上最强运动的总体分布却极不均匀。

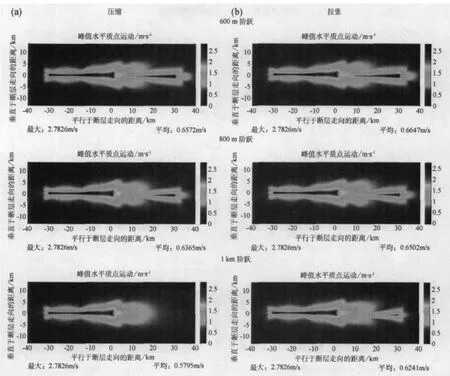
图6 峰值水平质点运动的分布：嵌于均匀花岗岩中亚剪切破裂速度的（a）压缩阶跃和（b）拉张阶跃，阶跃宽度600m、800m和1km。所有亚剪切图的颜色刻度最大值与这些模型中的最大地震动相对应。注意，压缩和拉张情况下运动的分布非常类似，但拉张情况下均有较高的平均地震动。还应注意1km压缩情况下的破裂未能跳过阶跃

3 讨论

3.1 阶跃与平面

阶跃断层比等长度的平面断层具有更低的地震动峰值，这是因为破裂在第一断层段末端停止，然后必定在第二段再次起始。假如没有几何复杂性，导致新起始所需的能量可以以更高的滑动速率和不断增加的方向性保持更高能和连贯的破裂前沿。事实上，单段长度的平面断层具有与任何阶跃情况相同的地震动峰值，表明第一段的破裂占地震动分布的主导地位，而且在第二断层段再次起始的破裂不能达到当前研究模型空间内初始破裂前沿的能量水平。破裂在第二断层段需要再次起始也打破了破裂的方向性；即使阶跃情况断层滑动的长度与平面断层完全相同，阶跃也会将滑动分布在两个（平行）方向，与平面断层的单一方向不同。

3.2 拉张与压缩阶跃

第二断层段上拉张和压缩阶跃间地震动峰值分布的主要差异与第二断层段的动态夹紧和松开有关（Harris and Day，1993）。

图7 嵌于均匀花岗岩中超剪切破裂速度的1km、2km、3km和4km阶跃峰值水平质点运动分布。（a）压缩阶跃，（b）拉张阶跃。颜色刻度的最大值与这些模型中的最大地震动相对应。1km的压缩情况平均地震动较高，但2km、3km和4km的拉张情况平均地震动较高。还应注意第二段的破裂在拉张情况总是在第一段末端起始，而在压缩情况阶跃宽度增加时，起始点迁移至沿第二段断层走向更深的地方

在压缩阶跃中，第二段的末端被第一段上的滑动引起的法向应力模式夹紧。这一位置点上法向应力的增加对破裂有障碍的作用；第二段上新的破裂前沿必定沿断层走向更远一点的地方起始以绕过这个障碍。阶跃越宽这种效应越明显，因为动态夹紧影响了沿断层走向更宽的范围。因此，两个断层段之间的间距更宽时，破裂沿第二段走向更远一点的地方起始。在拉张阶跃中，第二段的末端通过第一段的运动逐渐松开；这种局部法向应力的减少使得破裂在第二段更容易再次起始。沿断层走向（因此还有阶跃的宽度）松开的程度不影响新破裂在何处起始；它总是在沿断层走向的第一段结束的点开始，因为那里的松开最明显。这种效应说明了超剪切情况中第二段上起始点周围有较高运动区的原因：如果该段不受前一段影响或被前一段夹紧，其起始则需要更少的能量，因此更多的能量可以进入波的辐射。这一脉冲之后运动的减少或许是由于破裂前沿移出了断层松开的部分；一些能量需要返回以维持破裂直到获得足够的高能触发更高的地震动。

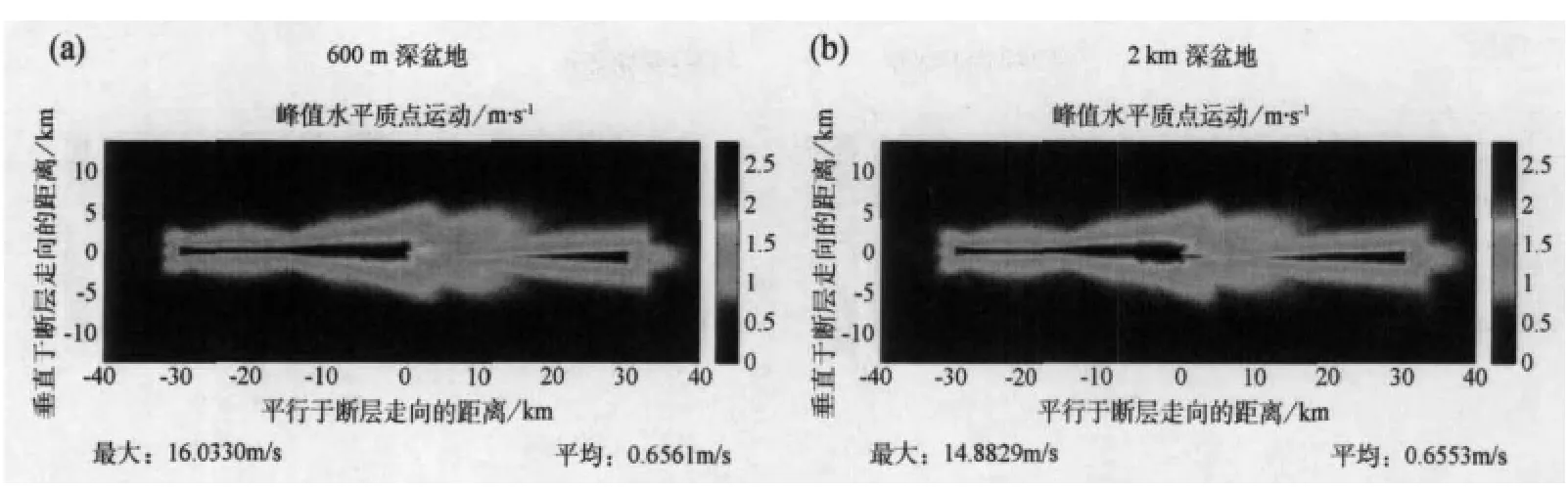
图8 断层段之间有沉积盆的亚剪切破裂速度800m拉张阶跃峰值水平质点运动的分布。（a）600m深盆地的结果，（b）2km深盆地的结果。该图设置的颜色条，使其最大值与嵌入均匀花岗岩中具有相同几何形状和应力状态的阶跃的峰值质点运动相对应。这些情况中的地震动峰值主要集中在盆地自身区域，在两个断层段之间。尽管这一地区受运动强度的影响，但盆地的存在并不对断层周围运动的分布有很大影响

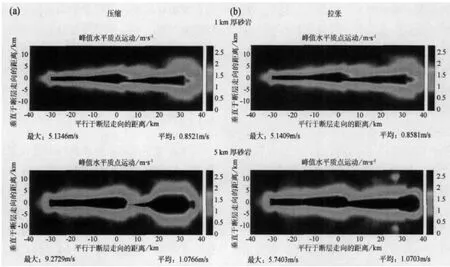
图9 嵌入花岗岩基底半空间之上砂岩层区域亚剪切破裂速度800m阶跃的峰值水平质点运动分布。（a）压缩阶跃，（b）拉张阶跃。上图为1km厚的砂岩层结果，下图为5km厚的砂岩层结果。图上设置的颜色条，使其最大值与嵌入均匀花岗岩具有相同几何形状和应力状态的阶跃的峰值质点运动相对应。在1km砂岩层的模型中，拉张和压缩阶跃之间地震动强度和分布的差异可以忽略不计，但阶跃类型的差异在5km厚砂岩层模型中极为明显

总之，动态夹紧和松开影响了沿第二断层段走向起始的位置。这反过来又导致了简单的方向性效应：破裂扩展的距离越远能量越高，同时引发更高的地震动。因为再次起始总是出现在拉张阶跃的同一位置，但在压缩阶跃中沿断层走向移动得越来越远，这种方向性效应有利于较高地震动在拉张阶跃中有更宽的分布。

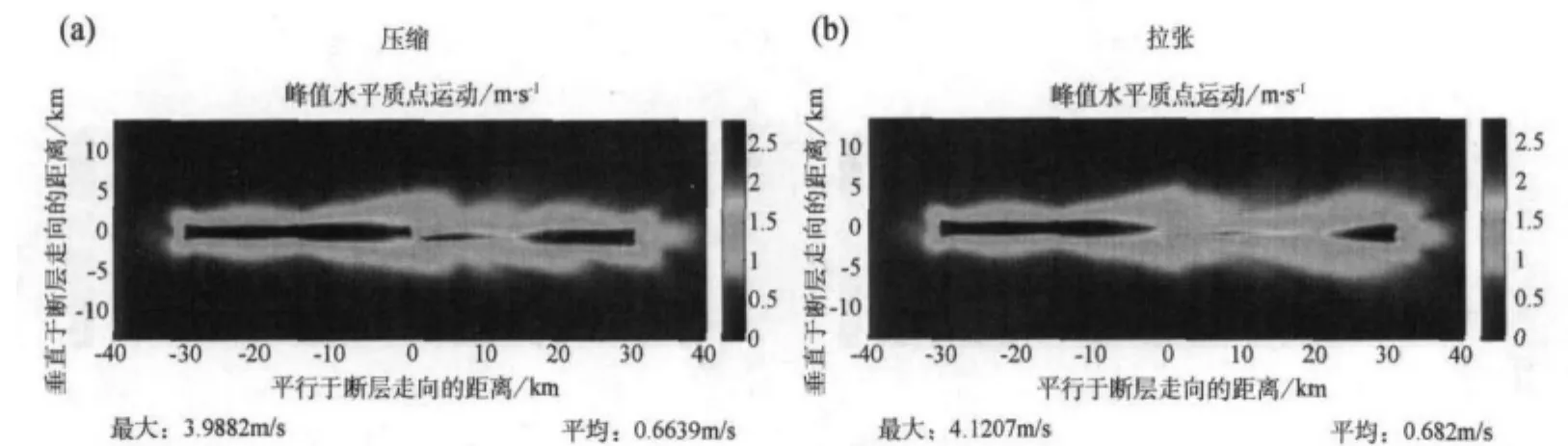
图10 由破坏区包围的亚剪切破裂速度800m阶跃的峰值水平质点运动分布。（a）压缩阶跃，（b）拉张阶跃。图上颜色条的设置，使其最大值与嵌入均匀花岗岩中具有相同几何形状和应力状态的阶跃的最大质点速度相对应。注意，压缩和拉张情况第二断层段周围运动的分布都不对称

对于亚剪切破裂速度的情况，这个主要的方向性效应内部及其自身就足以解释为什么拉张阶跃始终如一地产生比压缩阶跃更宽的强地震动分布。然而，仅仅这一效应无法解释所有超剪切破裂速度模型中第二段在拉张或压缩情况下是否有更高地震动之间的交叉。这种交叉行为由与再次起始破裂前沿是否与第一断层段停止阶段的通过一致有关的第二个方向性效应得到了解释。图11显示了超剪切破裂情况应力在起始时间在第二断层段上的快照。红线代表屈服应力，蓝线代表剪切应力；两条线的交叉点便是破裂前沿。值得注意的是，在压缩情况下，破裂前沿正好在表示停止阶段的剪应力峰值上，而在拉张情况下，破裂前沿稍落后于停止阶段。对于1km的阶跃宽度，压缩和拉张情况下破裂均大致在沿断层走向相同的点上起始。停止阶段因此可以为压缩情况下的破裂前沿提供足够的能量，与整个断层段下面扩展引起的方向性结合，就能够释放比拉张情况更高的地震动，这个拉张情况仅有断层破裂引起的方向性效应。然而，对4km的阶跃，破裂在压缩的情况下沿断层走向起始的距离这么远以至于在方向性之前断层端部就可重建起来，而且来自停止期的能量增加没有为破裂提供足够的能量，使得该破裂引发比拉张阶跃更高的运动。这个第二方向性效应在亚剪切破裂速度模型中未起作用。亚剪切破裂情况下第一断层段破裂末端与第二段破裂再次起始之间的时间比在超剪切破裂的情况下更滞后，这使得停止阶段在新的破裂前沿形成前就超过了次级起始点。

3.3 材料的对比

地震动在所有非均质材料设置模型中的分布，都由滑动深度和破裂前沿的连贯性控制。在均匀花岗岩中，第二断层段上的破裂在约2.5km的下倾处起始，无论阶跃是拉张还是压缩。这个结果也适用于拉分盆地拉张阶跃模型；盆地表观太小或太浅，就不能对破裂起始的地方产生显著的影响。在以花岗岩为基底的1km砂岩层模型中，拉张和压缩情况下破裂均正好在花岗岩和砂岩之间的交界面起始，导致几乎具有相同地震动模式的两个阶跃类型。然而，在5km的砂岩层模型中，拉张情况下的破裂在砂岩—花岗岩交界面起始并向上扩展，直到跨越孕震层的最大深度，而在压缩情况下破裂恰好在表面起始并向下扩展。这又凸显了另一个方向性效应：在深处起始的破裂向上扩展并同时沿断层走向扩展，向表面集中能量，导致更强烈的运动。在表面起始的破裂虽然表面震动强烈，但这种破裂的能量实际上是向下传播的。在这点上，我们不能解释材料的对比是如何控制第二断层段起始深度的。

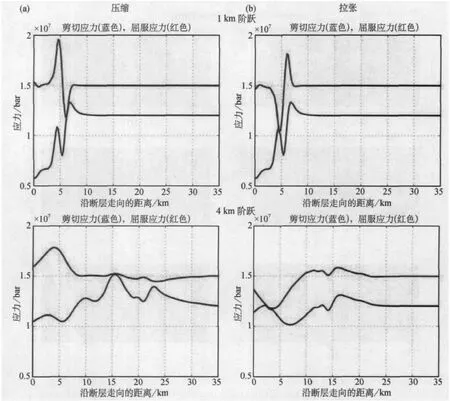
图11 嵌入均匀花岗岩中超剪切破裂速度的阶跃在破裂起始时刻第二断层段上8km深度的应力快照。上图为1km阶跃，下图为4km阶跃，（a）压缩情况，（b）拉张情况。红色曲线（原图为彩色图——译注）代表屈服应力，蓝色曲线代表剪切应力；这两条曲线的交汇处为破裂前沿。在1km的阶跃，破裂在拉张和压缩的情况下沿断层走向大致相同的点起始，但需要注意，压缩情况下破裂的前沿恰好与代表第一断层段停止阶段的剪切应力峰值一致，而拉张情况下破裂前沿在停止阶段之后才起始。在4km阶跃，破裂前沿在拉张和压缩的情况下都不与停止阶段相对应，破裂在压缩情况下比在拉张情况下在沿断层走向更远的地方起始

破坏区模型特别强调了最高滑动发生的深度对表面运动的影响。图12显示了拉张破坏区情况的快照，表明了破裂前沿从一组断开的小破裂前沿到单一连贯破裂前沿随时间而发生的演变。在压缩模型中，破裂在表面正下方起始，但在拉张模型中，主要的起始发生在约5km的深度，表面正下方和断层底部正上方有较小的次级前沿。我们对这种多重起始现象没有作明确的解释，虽然我们猜想，第一断层段周围的破坏区产生了足够异构的破裂以至于导致第二段上松开的分布不均匀。如果强应力扰动袭击第二段，而第二段对破裂足够有利，起始就没有理由不发生在多个点。另一个可能的解释是，波陷于破坏区并进一步放大，导致了次级断层上复杂的应力模式。深处滑动速率较高的地区，在空间上对应表面较高的地震动，而表面上较高的滑动速率却转化为较低的地震动。这种效应发生在破裂前沿仍互不连贯的情况下；一种可能的解释是，破裂前沿混乱的自然属性致使波能量在不同的时间到达且无助于地震动峰值。一般情况下峰值滑动速率越向表面集中破裂前沿在深部越不连贯。破裂最终合并成连贯的前沿，并覆盖第二断层段上沿走向约15km的孕震层绝大部分深度；正是在这一点上，地震动随传播距离增加而加强，如在均匀花岗岩模型中。

图12 被破坏区包围的亚剪切破裂速度800m拉张阶跃第二断层段深处滑动速率的快照。注意前5个快照破裂前沿的不规则形状以及其形态随时间演变的情况。断层前沿的形状和滑动速率分布在第六个快照中已大大稳定。破裂前沿的这种不对称性归因于断层周围地震动的不规则分布，如图10所示

在所有这些情况下，密度较低或波速较低的材料，正如预期导致了较高的地震动值。在破坏区和以花岗岩为基底的砂岩的情况下，地震动的空间模式不同于均匀花岗岩情况，表明材料间的界面对这个模式有影响。如果界面不参与对破裂行为的影响，地震动的分布会出现与在均匀情况下相同的情况，虽然更兼容的材料会导致向上扩展的情况。

4 总结和结论

有阶跃的断层有不寻常的地震动分布模式，不同于与平面断层破裂有关的沿断层走向运动分布范围越来越宽。压缩与拉张阶跃引起的运动的分布之间存在一些共同特征：峰值运动与第一断层段上的起始有关，运动减少区在第一段的末端，第二段上再次起始后沿断层走向强运动再次增大分布。这些特征在大小应力降和超剪切及亚剪切破裂速度时仍保持一致。在拉张与压缩情况之间地震动分布的差异在超剪切破裂速度的情况下变得更明显：第二段上的拉张阶跃在沿断层走向第一段末端的点有一较高运动的小区，压缩阶跃沿第二段有不对称运动的分布和阶跃外侧有更强的运动。断层段之间间距的增大减小了第二断层段周围运动的强度和分布。应力降的增加提高了两个断层段运动的强度，但不能定性地改变断层周围地震动的模式。

在亚剪切破裂速度的模型中，拉张阶跃比压缩阶跃始终有更高的地震动峰值和更宽的较高运动分布。这样的结果归因于简单的方向性效应，而这个效应反过来受阶跃的动态夹紧和松开的控制。拉张阶跃中的松开可使破裂总是在沿断层走向第二段上的第一段结束点上起始。拉张阶跃中的夹紧导致第二段上的起始点沿断层走向随断层段之间的间距变宽而移动到更远处。因为拉张情况下的破裂沿断层的走向扩展更大的距离，这就比在压缩情况下形成了更多方向性且产生更高的地震动。然而，在有超剪切破裂速度的情况中，压缩阶跃宽度越窄，地震动越高，拉张阶跃宽度越宽，地震动越高。该转变由第二方向性效应控制：第二断层段上破裂的起始是否与第一段的停止期巧合一致。这种一致仅发生在压缩阶跃；当压缩情况的起始点接近沿断层走向拉张情况的起始点时，由停止期提供给破裂前沿的额外能量使压缩情况比拉张情况有更高的运动，但是如果破裂沿断层走向起始太远，这种效应就不会成为地震动的主要因素。

虽然材料性质确实能够直接影响运动的强度，但用比较快波速的较硬材料与较慢波速的较软材料之间简单的标度关系更复杂的方式，介绍沿断层阶跃现实材料的对比改变了地震动的分布。在这些情况中，材料性质和界面影响了第二断层段上破裂起始的深度。在深部起始的破裂比在表面起始的破裂在表面产生更高的运动，这归因于破裂前沿沿断层走向扩展的同时也向上扩展的方向性效应。在整个破裂过程中下倾滑动速率的分布对地震动产生影响：如果最高滑动速率的深度随破裂扩展发生变化，表面运动的分布将会不对称，但一旦破裂在横跨断层大部分孕震深度的连贯前沿中稳定，表面上的运动在断层的任何一侧都会呈对称分布而且更强烈。

数据与来源

本文没有使用外来数据。所有结果使用FaultMod（Barall，2009）产生，所有图件使用MATLAB或Adobe插图软件生成。