利用地震波干涉法探求衰减结构的理论背景

中原 恒

引言

基于地震波干涉法并利用振幅信息来推定介质衰减构造是否可行，已成为近年来的重大课题。回顾该课题截止到目前的研究，首先是理论探讨：Snieder（2007）对衰减波动方程的相反定理进行证明，揭示了在非均匀介质中，噪声源只有在补偿衰减效果后分布的情况下地震波干涉法才严密成立这一结果。Weavers（2008）应用量子场论中的Ward恒等式与地震波干涉法的等价性，揭示了对于含有波动方程的一般线性微分方程，从场的相互作用中提取格林函数的方法。Margerin和Sato（2011）揭示了若要在非均匀的衰减性介质中使地震波干涉法成立，那么也必须使广义光学定理成立。不论哪一种理论都揭示出，只要满足特定的条件，即使在衰减性介质中，地震波干涉法也能成立。

此外，还通过数值计算进行了检验。例如，Cupillard和Capdeville（2010）揭示出：在考虑球状地壳构造的情况下，当噪声源在地表呈空间均匀分布时，就可以正确推定其衰减，但当噪声源为局部存在时，就无法进行正确推定了。相同的数值验证也经Weaver（2011）得出了结论。

在实际数据分析中，Snieder和Safak（2006）通过对同一建筑物内不同楼层的地震记录进行反褶积，把在建筑物内呈上下传播的波分离，由振幅比成功推定出了建筑物的Q值。另一方面，Prieto等（2009）基于地震波干涉法，推定了南加利福尼亚地区的衰减结构。更严谨地说，他是以物理性的直观，根据Aki（1957）提出的非衰减性介质中空间自相关法公式，提出了噪声源在衰减性介质中扩散的公式，并以此作为基础。Tsai（2011）对其公式进行了理论上的探讨，但这个公式是严密解还是近似解，仍未可知。最近，Nakahara（2012）针对一维、二维和三维的均质衰减性介质，已将空间自相关法的公式成功定式化。特别是基于针对二维的结果，Prieto等（2009）的公式并非严密解，但其在衰减较弱的情况下基本接近真实解，这已在理论上明确。在证明过程中，由于空间自相关法与地震波干涉法的理论关系起到了重要的作用，所以这部分不仅引用以往的论文，还向大家说明问题存在的客观性。

本论文在重视理论连贯性的前提下，将采用地震波干涉法推定地下衰减构造这一目标的理论背景进行明确。首先详细证明衰减性介质中的空间自相关法和地震波干涉法的理论关系式，在此基础上，揭示了Prieto等（2009）提出的利用两者之间关系推定衰减构造的具体方法。

1 衰减性非均匀介质中地震波干涉法的证明

首先对衰减性非均匀介质中地震波干涉法进行证明。同时，采用以下的衰减波动方程：

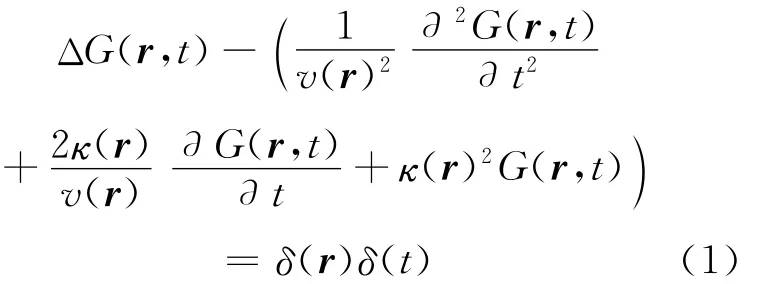
式中，G是衰减波动方程式的格林函数，r是空间，t代表时间，v（r）代表速度，κ（r）代表衰减，考虑到了非均匀介质的情况。这一方程，先被Margerin和Sato（2011）采用，然后既作为波动方程中的一例（今村，1978），又作为电报方程（Courant and Hilbert，1962）中的一例被研究。关于此方程各项物理意义，今村（1978）利用橡胶涂层包裹琴弦的振动进行了说明。根据这一说明，左边第3项是与速度成正比的摩擦力，左边第4项是由橡胶弹性决定的复原力。下面，证明的过程与Snieder（2007）相同，只是采用的衰减波动方程在形式上略有差异。本论文采用（1）的衰减波动方程的理由，也将在后面进行讨论。Q值与频率成正比，衰减时波形形状不变，只有振幅发生变化，因此方程相对简单。

将（1）式从空间—时间域变换到空间—频率域，可得出下面的亥姆霍兹方程：

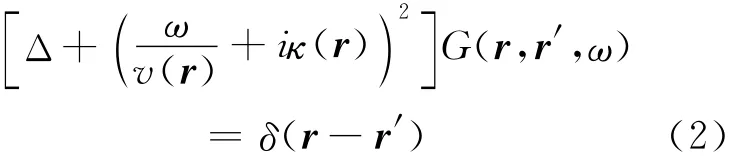
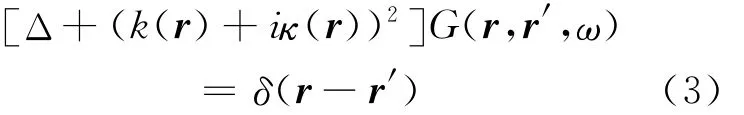
设震源为r1时，方程如下：

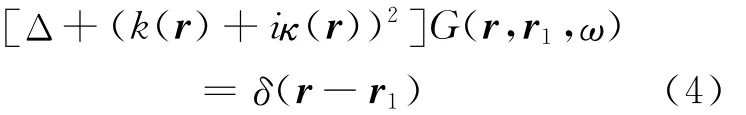
在频率域采用的复共轭与时间域中的时间反转相对应。对于时间反转场，若震源为r2时，

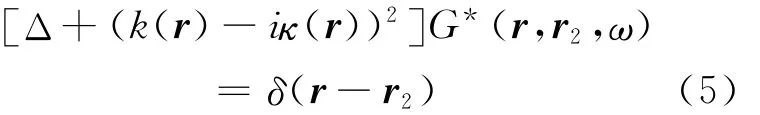
成立，其中＊代表复共轭。将（4）式与G＊的乘积和（5）式与G的乘积进行减法运算，并体积分，结果如下：

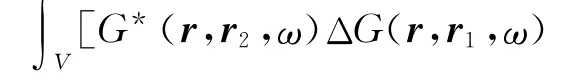
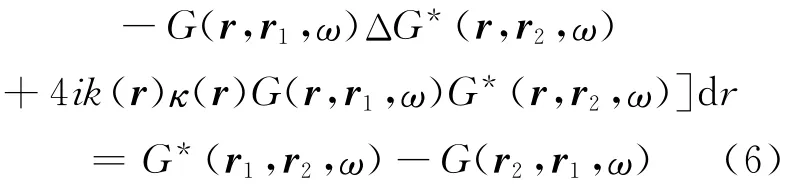
V表示体积分的积分域，对于左边的第1项与第2项，还可以采用高斯散度定理将体积分转变成面积分：

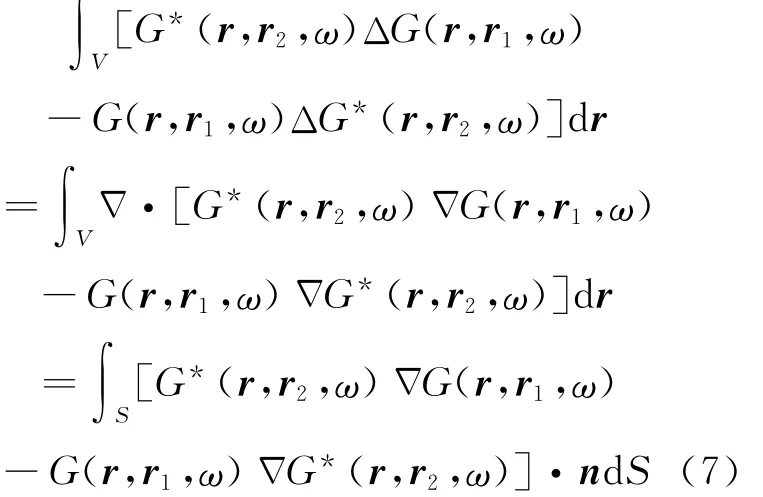
S为面积分的积分域，n为S的单位外法向量。综上所述，可得出：

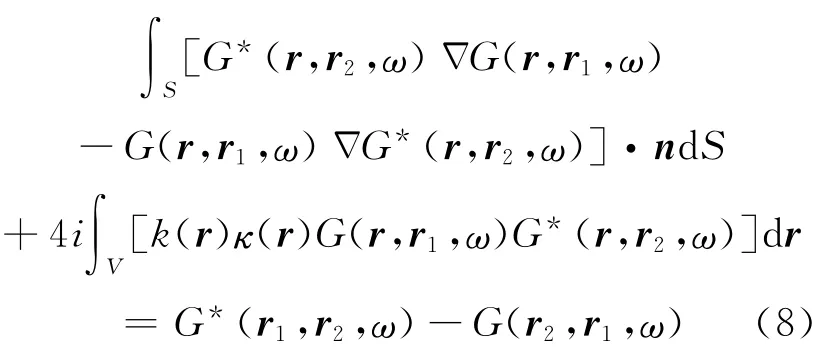
整理后如下式：

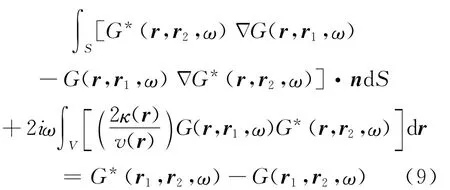
方程右边，有关格林函数的方程，是利用了震源和观测点可以互为替换的特性。鉴于无限介质在放射条件下无限远传播的波动场为零，因面积分的影响可以忽略，仅用体积分就可以表示如下：

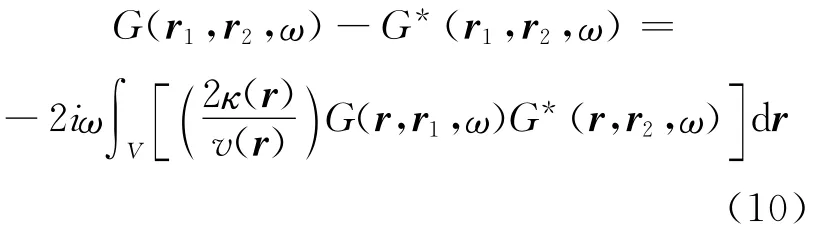
公式中，右边的－iω表示与时间微分对应，左边还可以进一步替换，如下表示：

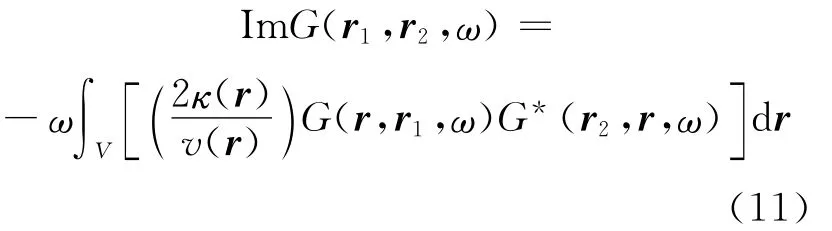
Im表示的是虚数部分，右边再次将震源和观测点进行替换。右边的格林函数与其复共轭的积，是与位置r的脉冲震源观测点r1，r2处波动场互相关的计算结果相对应的。由公式可知，为使地震波干涉法成立（从互相关提取格林函数），在取得右边互相关的同时，也要考虑对速度和衰减依存程度。也就是说，噪声源的分布为2κ（r）／v（r），就是对衰减影响进行的适度补偿。这在Snieder（2007）中最早被提出来。但是，在实际操作中，这种绝佳的平衡是很难达到的。特别在介质构造不均匀的情况下，复杂的噪声源分布客观存在，地震波干涉法能否严密地成立，还应认真慎重地研究。

2 空间自相关法与地震波干涉法的理论关系

前面已经对非均匀衰减性介质中采用的地波干涉法进行了证明，接下来要探讨空间自相关法与地震波干涉法之间的关系。这个问题的设立如图1所示。首先，选取衰减性无限介质中的两个观测点（三角形标记），假设噪声源（星形标记）在介质中呈体积分布。在这种情况下，可以对两点间的波动场进行标准化的交叉谱分析，明确其与格林函数之间的理论关系。此外，在无衰减的情况下，由于假设平面波向观测点各向同性入射（例如，Nakahara，2006；Sanchez－Sesma and Campillo，2006），因此必须注意条件的变化。

假设两个观测点的位置分别为r1、r2，这时频率域的波动场用u（r1，ω）、u（r2，ω）表示。这两点的波动场的标准化交叉谱C1，2（r，ω）可定义如下：

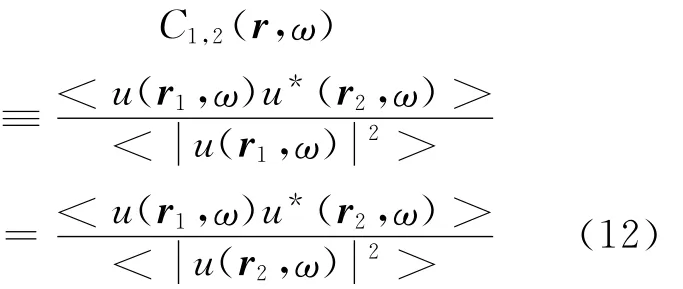
式中＜＞是样本平均，用r＝r2－r1表示。在（12）式中取等号时，假设波动场的空间稳定：

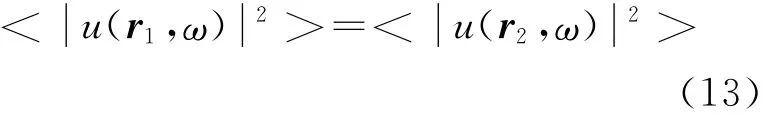
接下来分析由噪声源生成的波动所构成的波动场，可通过噪声源光谱N（r，ω）与格林函数表示如下：

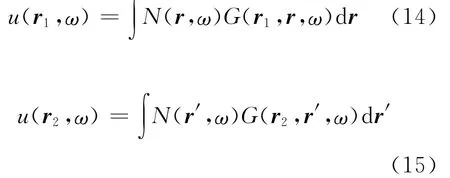
假设不同情况下的噪声源无相关性，那么

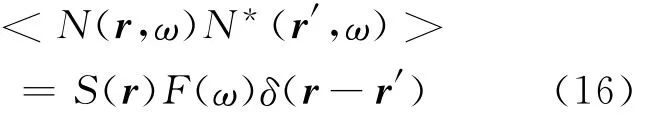
式中，S（r）是噪声源的分布强度，F（ω）是功率谱。假设所有噪声源都具有共性，那么通过以上讨论可得出：

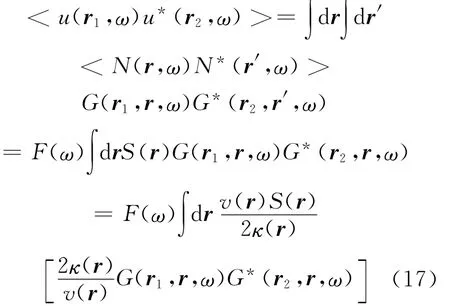
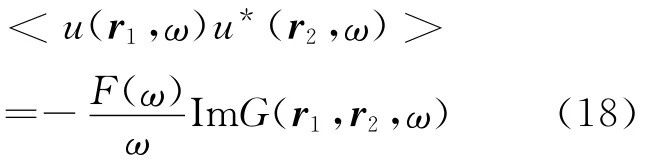
虽然格林函数在频率域略有扭曲，但由于SPAC法中（12）式的分母和分子可以约分，所以代入后可导出：

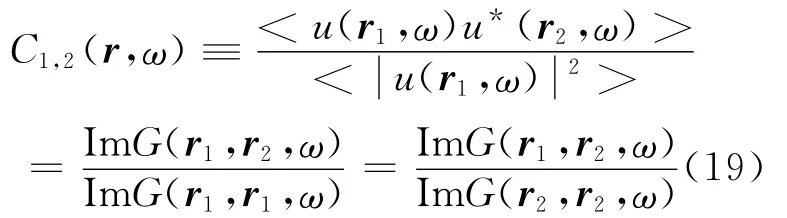
这就是空间自相关法与地震波干涉法相互关联的理论关系式。也就是说，当（18）式成立时，（19）关系式也成立，但由于空间自相关法是对各频率独立进行计算，所以格式函数在频率稍有扭曲也不构成问题，与地震波干涉法相比，对条件的要求能略有宽容。另外，空间自相关法与地震波干涉法相互关联的关系式在非衰减性介质的情况下，已由Nakahara（2006）针对纯量波以及 Sanchez－Sesma与Campillo（2006）和 Yokoi与 Margaryan（2008）针对向量波推导出来了。本研究的创新点在于，（19）关系式对于衰减性介质也成立。这里特别需要强调的是有关噪声源的分布。在非衰减性介质中，必须是Aki（1957）中阐述的平面波入射（即远处某噪声源呈观测点围绕分布）；在衰减性介质中，噪声源必须呈体积分布。

3 关于Prieto等（2009）中算式的理解

前一节中针对非均匀的衰减性无限介质，导出了空间自相关法和地震波干涉法的理论关系式。本节将基于上述结果来了解Prieto等（2009）中的算式。

目标确立，就必须要有附加条件。首先讨论均匀的衰减性介质（速度、衰减以及空间分布均匀的状态下）。从（11）式可知，地震波干涉法严密成立时，要求噪声源呈空间均匀分布状态。也就是说κ、v都是不变的。在Nakahara（2012）中，（19）式对于均匀的衰减性无限介质成立，已众所周知。将（1）式的波动方程中的格林函数（参见今村，1978）代入（19）式后，就能成功地将空间自相关法扩展应用到衰减性介质。虽然其中包括一维、二维和三维不同情况下的特定应用，但由于本文的目的是了解Prieto等（2009）的算式，所以仅针对二维情况下的结果进行简单的讨论。

在二维情况下，格式函数用0次的第1种汉克尔函数H（1）0（x）表示。将其带入（19）式后，可导出以下严密式：

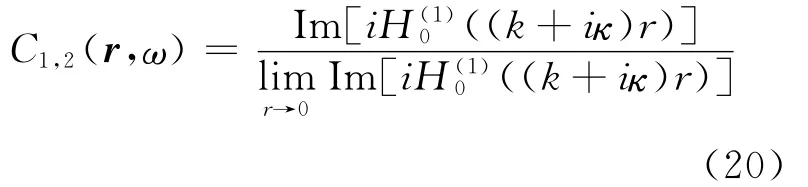
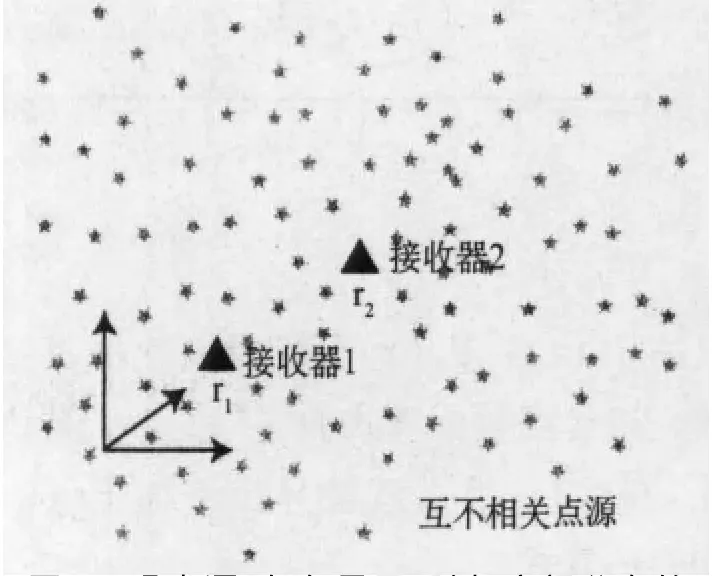
图1 噪声源（灰色星号）随机空间分布的衰减性介质模型设置。两个台站用实心三角表示。示意说明了三维坐标系

该算式可以进行定量评价，但很难进行深入分析。因此，要附加两个条件：衰减要小（κ／k≪1）；观测点之间的距离要远大于波长（kr≫1）。首先，格林函数的远场近似如下：

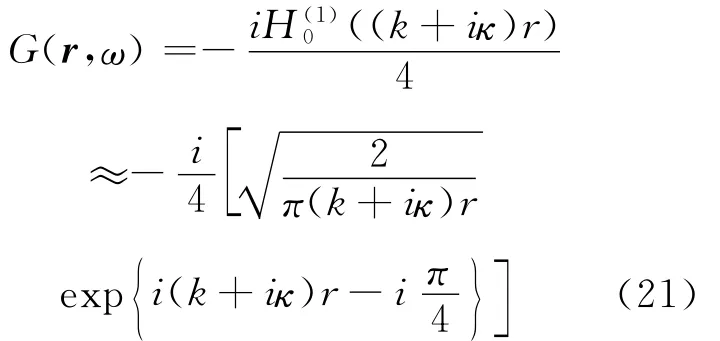
而且（20）式的分母计算要使用到下面的关系式：

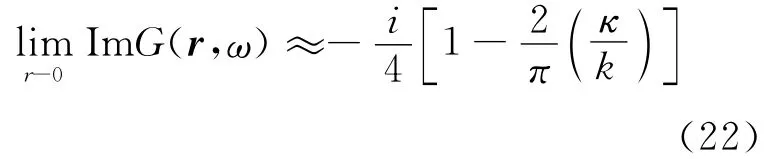
这与Nakahara（2012）的（27）式相对应，但在弱衰减的近似计算中，格林函数要展开到κ／k的一次项为止，而且要取0次贝塞尔函数与一次纽曼函数参数设为零时的极限。利用以上算法，当只剩下κ／k的一次项后，由（20）可导出：

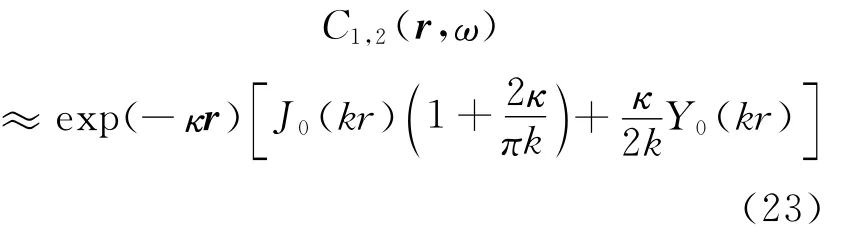
这里的J0（x）、Y0（x）分别是0次的贝塞尔函数、纽曼函数。算式的 ［ ］中，若满足条件κ／k≪1，那么就能导出下面Prieto等（2009）的算式：

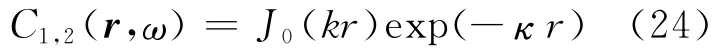
综上所述，对于（20）式的严密解来说，只要满足衰减小、观测点间距远远大于波长这两个假设条件，理论上就能够导出Prieto等（2009）的算式。

4 讨论

首先，要讨论本研究的理论制约条件。空间自相关法与地震波干涉法的理论关系式（19），是在设定（1）式的衰减波动方程后，针对非均匀衰减性无限介质导出的结果。要使这一结果成立，地震波干涉法也必须成立，要求噪声源的分布能够满足较好补偿衰减影响这一条件。当这一条件无法满足时，就会出现假象。事实上，噪声源的分布与所要探知的地下构造有着复杂的联系，由此可见，确认噪声源分布的有效性并非易事。当然，噪声源的分布要针对衰减性介质和非衰减性介质分情况考虑。但是，对于非衰减性介质，我们都知道，像Aki（1957）那样利用圆排列来计算方位角平均，就能够消除假象。但是，对于衰减性介质，即使利用圆排列也无法消除噪声源分布的不均匀性。这就是（11）式有必要对噪声源进行体积分的原因，因为通过方位角平均可以除去方位角方向的非均匀介质，却无法去除径向方向的非均匀介质。

接下来，（20）关系式是针对均匀衰减性介质，由假定的衰减波动方程（1）推导出来的。（1）式只是衰减波动方程的形式之一，Snieder（2007）和 Tsai（2011）中所采用的波动方程去掉了（1）式的左边最后一项。这种不同取决于Q值与频率之间的依赖关系（Nakahara，2012）。算式（1）中，Q 值与频率成正比，波形无变化，只有振幅有变化，所以是最简单的情况。Snieder（2007）中采用的减衰波动方程式，由于Q值与频率之间的依赖关系较复杂，所以解析起来很难。仅当衰减κ很小时，两者的差异由于与κ2成正比，所以可以忽略不计。若能将衰减波动方程顺利地转换成线形微分方程，如Sato等（2012）所指出的那样，利用Resalvent公式就可证明地震波干涉法的成立，但是若一般情况下Q值与频率之间的依存关系无规律可循时，证明起来就会相当麻烦。

在本研究中，针对均匀衰减性介质，在假设衰减很弱且观测点间距远远大于波长的基础上就能够推导出Prieto等（2009）的算式。Nakahara（2012）针对衰减κ＝0.01k（Q＝50）和κ＝0.1k（Q＝5）两种情况，在0≤kr≤10的范围内，对三个算式（20）、（23）、（24）对行了比较。确定了不论哪种情况下，当kr≠0时，三个算式在5%范围内均存在一致性。也就是说，当衰减很弱时（κ≤0.1k），Prieto等（2009）的算式结果是十分接近的。Prieto等（2009）利用周期在7.5s到20s区间，观测点间距在500km以内的数据进行了解析。相关参数如表1所示，kr的最大值为45～140，衰减系数与κ＝0.002k—0.01k相对应。图2是当κ＝0.01k和κ＝0.1k时，将（20）、（23）、（24）式的极小值（负值）绝对值与极大值用直线连结的包络线用对数表示后的结果。这与Prieto等（2009）的图6相对应。由此可见，衰减的大小在kr≫1的范围内可通过曲线的斜率进行推断。此外，通过图2的双图可知，3个公式几乎一致。通过表1我们能够确定，在左图κ＝0.01k且逐渐减少的情况下，Prieto等（2009）的解析可以在近似成立的范围内进行。

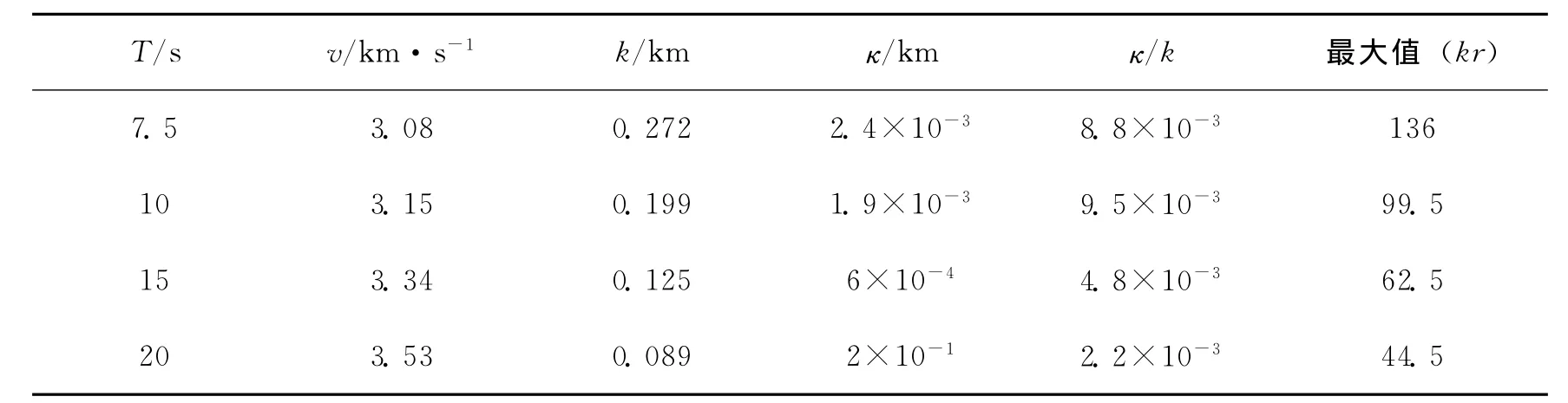
表1 Prieto等（2009）使用的参数

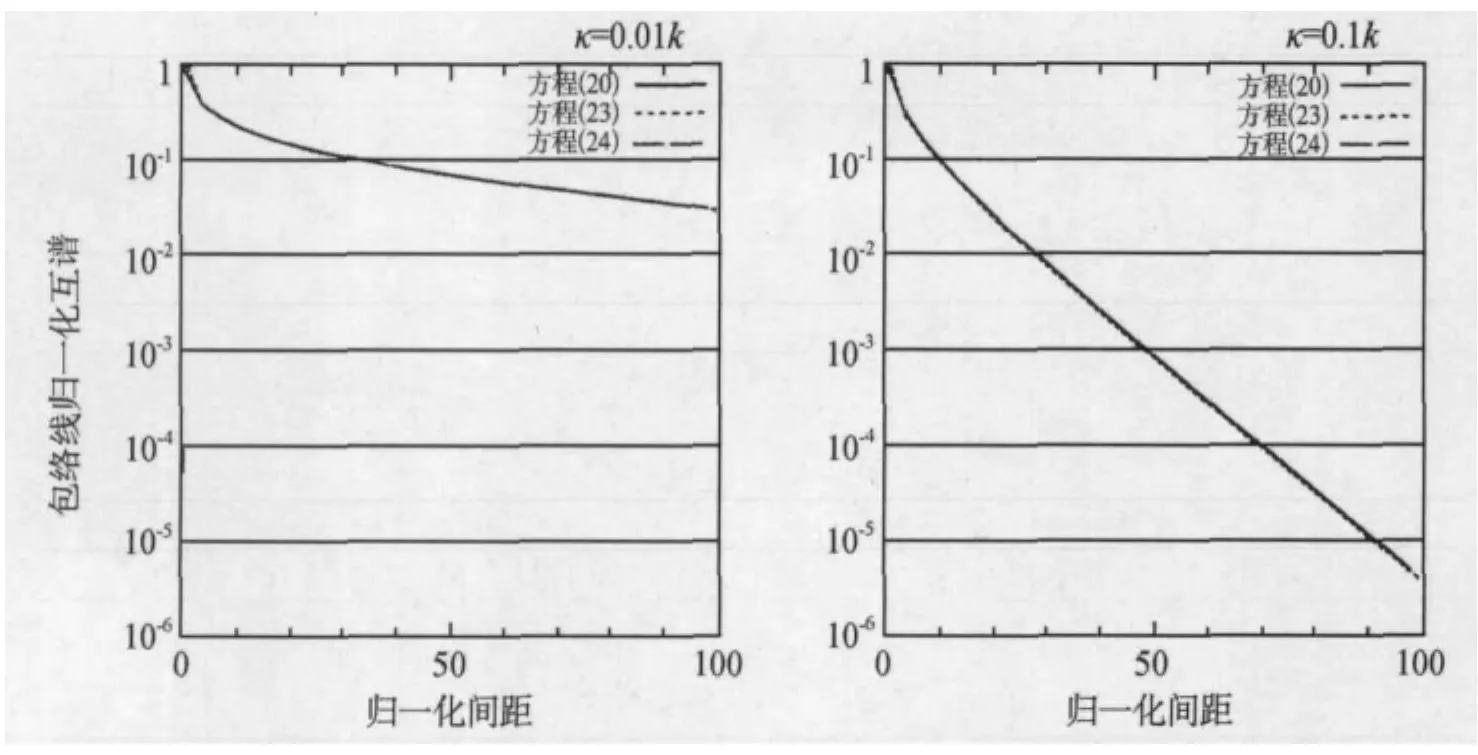
图2 包络线归一化互谱与归一化台站间距kr关系。方程（20）、（23）和（24）的包络线分别用实线、点线和虚线表示。к＝0.01k（左图）和к＝0.1k（右图）

另一方面，近期Lawrence和Prieto（2011）基于Prieto等（2009）的算式，在美国西部对衰减构造进行了层析成像研究。但是，一定要注意，采用的公式是针对均质构造进行理论推导的结果。在非均质构造情况下，不能采用（20）式，要在（19）式中针对非均质构造使用格林函数进行计算，但现在这方面的理论研究还不是很充分。也就是说，针对非均匀介质的衰减构造，基于（24）式进行衰减成像的合理性，今后还有必要进一步验证。

5 结论

本论文对利用地震波干涉法推定衰减构造的理论背景进行了考察。针对非均匀衰减性介质的地震波干涉法进行了探讨，证明了地震波干涉法在仅当噪声源的分布能很好补偿衰减时严密成立。进一步导出了空间自相关法与地震波干涉法的理论关系。在那之后，为进一步理解Prieto等（2009）的内容，近来对采用空间自相关法推定衰减构造的方法进行了检查。其结果是：这一公式是针对均匀衰减性介质，在衰减小且观测点间距远远大于波长的情况下导出的是近似式。这一结果对空间自相关法和地震波干涉法的理论关系影响重大。基于这一结果，Prieto等（2009）的公式也应该适用于相对均匀的介质。在非均质领域中，层析成像的合理性还未明确，今后还要进行必要的理论探讨。