基于序列的地震危险性概率分析

I.Iervolino M.Giorgio B.Polidoro

引言

地震危险性概率分析（PSHA，如McGuire，2004）是评估特定区域地震危险性的综合过程。地震危险性概率分析，在传统模式中一般只涉及主震的发生。这些显著震级的事件是在时空上集中的事件序列内鉴别。

另一方面，地震序列中的余震可看作是由主震触发的。每个序列的特征被认为只依赖于触发事件的震级和位置，是有条件地与过去的历史无关（随机意义上）。在这些前提下，Yeo和Cornell（2009）发展了余震地震危险性概率分析（APSHA）来表示类似于主震的余震危险性。事实上，余震地震危险性概率分析结果是用地震动强度测度（IM）阈值的超越概率表示。这对于主震后的应急期是很有用的，见 Yeo和Cornell（2005）的讨论。

地震丛集的发生被概率性地描述为与计算主震事件采用的相同随机过程可能会引起争议。本文中假定每个丛集的发生时间与触发地震的发生时间一致。事实上，从Toro与Silva（2001）和Boyd（2012）的研究开始，将地震危险性概率分析扩展到主震发生概率与序列期间至少超越一次地震动强度测度阈值的概率相乘看来都是可能的。这意味着只保留地震丛集中导致超越的事件而过滤掉其他事件。

从工程的观点，计算在地震序列发生期间涉及到超越地震动强度水平的地震事件（例如对结构关键的）发生率，实际上意味着也考虑余震引起结构破坏而主震没有引起结构破坏的概率。这就导致出了基于序列的地震危险性概率分析（SPSHA）方法，对基于性能的抗震设计是适合的。它允许确定设计强度的超越概率以考虑余震的潜在威胁（Iervolin，Giorgio and Polidoro，2013）。对于当前抗震规范的每次普通实践，忽略了对结构的累积损伤，而它可能对短期风险管理有意义；这一研究方向的某些结果参见Yeo与Cornell（2005）及Iervolino，Giorgio和Chioccarelli（2013）。

在下面的研究中，从对上述研究的直觉开始，导出基于序列的地震危险性概率分析的解析表达式，在地震危险性整体中包含了余震，而这在Toro与Silva（2001）和Boyd（2012）的研究中未包括。该方法基于的假设是，主震的发生由均匀泊松过程（HPP）调节，而余震的发生由有条件的非均匀泊松过程（NHPP）调节。假定属于一个给定序列的余震的发生率，其震级的范围和它们的空间丛集仅依赖于触发主震的震级和位置。在本文中，前震因为数量非常有限而予以忽略（Yeo and Cornell，2009）。

如下所述，余震的模型基于的是修订的大森定律（Utsu，1961）；因此，本研究可以视为是模拟主要余震。事实上，其他模型如传染型余震序列（ETAS；如，Ogata，1988）实际上能够模拟地震丛集，其中每个事件都能够产生它自己的序列。

这项研究不直接涉及有关地震去丛集的问题，而只依据主震最后的发生率和作为建议模型输入数据的修订大森定律的参数。另一方面，应该想到的是主震和余震获得的结果都与模型有关。这是因为，给定的原始地震目录中，丛集是在传统的规则基础上进行的，这是通过采用描述地震发生的模型来定义的。

本文的结构为首先对地震危险性概率分析和余震地震危险性概率分析方法的原理进行简要回顾。然后，解析性地讨论二者的结合，用一个地震危险性积分形式说明整个地震序列的影响。应用实例中考虑了一般的震源，使用基于序列的地震危险性概率分析方法对不同强度测度水平的年超越率进行计算，并对忽略了余震影响的传统地震危险性分析的相对差异的显著性进行评估。

1 主震、余震和地震动强度

本节简要地回顾用于评估主震和条件余震危险性、均以地震动强度阈值超越率表达的随机处理和解析公式。

1.1 主震危险性概率分析

地震危险性概率分析通常采用均匀伯松过程概率性地模拟在震源区产生的地震数量。均匀伯松过程是一个独立且稳定的增量（即，无记忆）过程，完全由一个参数即发生率νE描述。根据均匀伯松过程，发生在所关注时间间隔（t，t＋ΔT）的事件数NE与过去的历史地震无关，并具有泊松概率质量函数如式（1）：

对均匀伯松过程也自然得出，主震的到达间隔时间分布是指数分布，其中两者间平均到达时间为发生率的倒数。

在地震危险性概率分析中，对所关注区域，强度测度阈值的超越数im也由均匀伯松过程概率性地给出（Cornell，1968）。im的超越率λim，E由νE通过方程（2）得到，其中项地震动预测方程（GMPE）提供，表示对于一个给定震级为ME＝x和震中距范围RE＝y的地震强度阈值被超越的概率：

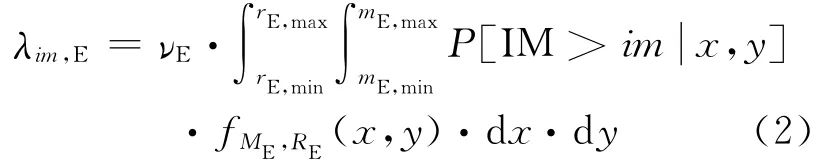
项fME，RE是主震震级和距离随机变量（RV）的联合概率密度函数（PDF）。在单个震源情况下，如果这两个随机变量可被认为是随机独立的，fME通常由古登堡—里克特（GR）关系式（Gutenberg and Richter，1944）给出，而fRE是基于震源—场地几何组构获得。积分限是由古登堡—里克特关系式约束的震级和确定可能RE值域的距离（Reiter，1990）。

1.2 余震地震危险性概率分析

余震地震危险性概率分析也由所关注区域超越地震动强度测度阈值的事件发生率来表示。与地震危险性概率分析的主要不同是该发生率是随时间变化的。自触发主震发生以来，每单位时间预期的事件数随时间的流逝而减少。这种意义上，描述余震发生的过程对于主震的发生和特征而言是必要条件。

用于构建余震地震危险性概率分析的非均匀伯松过程基于的假设是余震的日发生率νA｜mE（t）可以用方程（3）来表示，其中t为触发主震发生后消逝的时间，这里采用的时间轴为主震发生时t＝0。这个模型同样假设余震的震级在有意义的最小震级mmin与触发主震的震级之间。对于所考虑的地震序列，系数a和b来自适合的古登堡—里克特关系式，而参数c和p由修订的大森定律（Utsu，1961）给出。最后，给定触发主震的强度，序列中余震的强度都被假设为随机独立的随机变量：

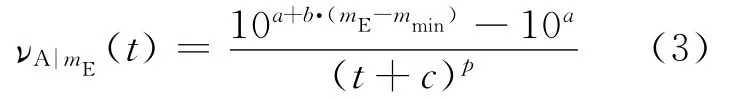
由式（3）可得，在时间间隔（t，t＋ΔTA）内余震的预期数量由方程（4）给出：

与地震危险性概率分析类似，余震地震危险性概率分析也通过事件的发生率与关注区域强度测度超越阈值的概率（时间的不变量）相乘来过滤地震过程的强度，减少事件的发生率。这使非均匀伯松过程的发生率λim，A｜mE（t）如方程（5），其中fMA，RA是一般余震震级和震源—场地距离的联合概率密度函数：

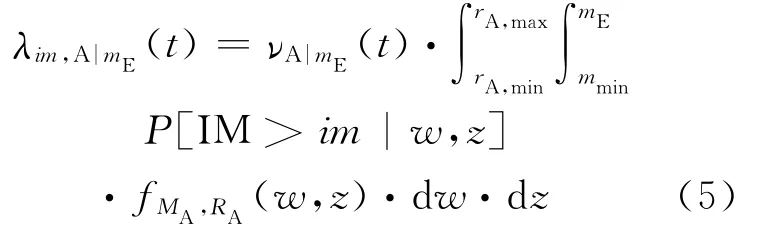
在上一节对fME，RE的考虑也同样适用于fMA，RA。余震的位置、震源距及其限定值｛rA，min，rA，max｝将在后面讨论。实际上，虽然在式（5）中的符号与Yeo和Cornell（2009）研究中的一致，但强度测度的超越率也依赖于主震的位置。

2 主震和余震随机过程的联合

在本节中，考虑主震和余震影响的地震危险性概率分析均用公式表示。序列的发生被描述成一个均匀伯松过程，而在一序列内，余震的发生被描述成非均匀伯松过程，其发生率函数对于触发事件的震级是必要条件。其目标还是评估地震动强度测度的年超越率（λim）。这里，这个考虑地震事件发生的发生率被定义为在序列内至少一次强度测度阈值的超越数，如式（6）：

式中强度测度是这个丛集内所有事件中地震动强度的最大值，IME是主震的强度测度，而IM∪A为余震中的最大强度。实际上，如果出现至少一次一个余震引起的强度高于这个场地的阈值，IM∪A就超过阈值。

根据余震地震危险性概率分析，余震序列的特征完全依赖于主震的特征。事件的数量、震级和位置是序列触发地震的大小和位置的函数。因此，对于主震的震级和位置的条件，定义为强度测度阈值的两个事件没有被超越：（1）在主震和（2）在任何余震中均是随机独立的，见方程（7）。（注意，它是由地震危险性概率分析和余震地震危险性概率分析模型得出的，与Boyd，2012的研究一致）

余震序列期间未超越阈值的概率已经公式化了，考虑了这种序列是由事件的随机数NA组成的情况。根据非均匀伯松过程假设，这种随机变量符合泊松分布，如式（1），还有式（4）给出的平均数。因此，将全概率理论应用于方程（7）中的项，方程（8）给出结果：

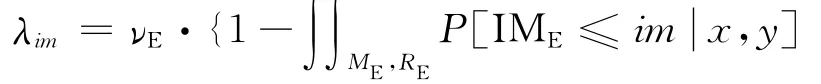
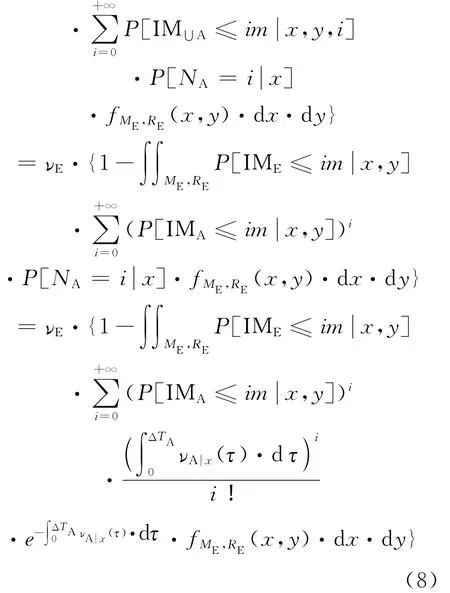
式中在i＝0时，P ［IMUA≤im｜x，y，i］＝1。νA｜x实际上反映的是该发生率依赖于主震震级，而ΔTA是余震序列的持续时间（该参数设定值会影响基于序列的地震危险性概率分析结果，因为ΔTA越大，NA的随机变量平均数越大，所以，强度测度超越率也越大）。每次余震地震危险性概率分析所有余震都相等（Yeo and Cornell，2009），是一般余震强度阈值的非超越概率，与其可能震级和位置相关，还是主震给定的震级和位置。

给定余震的震级和位置，强度测度阈值的非超越概率有条件地与主震无关。然后，根据全概率理论，对方程（8）中P ［IMA≤项重列公式，如方程（9）结果：

式中P ［IMA≤im｜w，z］项是已知震级和位置的一般余震的im非超越概率，而fMA，RA｜ME，RE是余震震级和震中距的联合概率密度函数，与主震的特征相关。这个概率密度函数对触发主震（下同）的震级和位置考虑了余震震级和余震孕震区的大小／位置的相关性。积分限分别对主震和余震在式（2）和式（5）中给出。

更简洁的地震危险性积分表达式如式（10）给出：

实际上，式（10）是使用式（11）等式得到的。

要注意的是，方程（10）的结果也能直接得到，在式（5）中通过发生率的非均匀伯松过程计算零级余震在（0，ΔTA）区间导致超越的概率。然而，给出公式的来源可以更深入了解在地震危险性积分中余震过程假设的含义。

用公式表示出单个震源情况下地震丛集的地震危险性积分后，就可能值得简要讨论对关注区地震危险性有贡献的多个震源（相互独立）的一般情况。在任一主震发生通过均匀伯松过程来模拟的情况下，对于所有震源，从式（9）得出的结果值只需求和。如果主震的发生在概率上用其他过程描述，例如更新过程，那么这个超越率值可能不是非时变的（讨论见Polidoro et al，2013）。这种情况下，如果修订的大森定律仍然适用于余震，那么就能够写出类似本研究中地震丛集的超越概率方程，然而得出的公式肯定不同。

推荐的这一方法也可以扩展应用到其他情况，在考虑地震丛集中任何地震产生其自己序列的可能性时用其他模型，如传染型余震序列模型（Ogata，1988），替代修订的大森定律来描述地震序列。这些模型会引起余震发生率的改变，而且可能影响主震的发生率。

3 应用实例

作为一个基于序列的地震危险性概率分析应用实例，计算了一般震源区中间的地震危险性，该区域大小是30×100km2（图1）。

3.1 主震和条件余震序列的特征

图1 主震震源、主震震中周围一般余震的网格及所关注场地

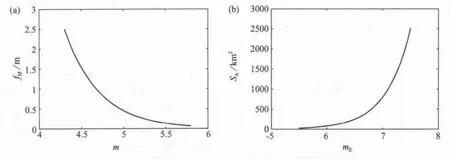
图2 （a）主震震级分布。（b）余震震源区面积与主震震级的关系

主震震中假定为在如图1所示的地震震源区均匀分布。为计算目的将图1划分成5×5km2的网格。主震发生率任意设为νE＝0.054个事件／年。主震的震级分布也任意设定为在4.3～5.8级区间范围的指数形式，如图2a。古登堡—里克特关系式的b值主震为1.056。在应用中，震级和震源距视为独立的随机变量。

假定每个主震都有由震中周围区域约束的余震。用平方千米表示的余震孕震区尺度SA通过式（12）由主震震级给出（Utsu，1970），如图2b。

在这个区域，任意指定一个方形区，划分成121个节点，震中均匀分布（见图1）。实际上，对地震危险性分析建议的方法可以处理任何形状的余震区（常用的如椭圆形）。另外，代表这个区域每个网格单元概率的任意函数都可以视为一个余震的位置（例如，概率密度函数有从主震的位置起的钟形径向衰减，如见Zhuang et al，2002）。然而，这个问题没有显著影响我们研究的结论，因此为简单起见考虑了在方形区的均匀分布。

在修订的大森定律和古登堡—里克特关系式中余震使用的参数，即式（3）中的参数，取自Lolli和Gasperini（2003）：a＝－1.66，b＝0.96，c＝0.03（天），p＝0.93，Mmin＝4.2。这些参数应用于意大利一般的余震序列；例如，Yeo和Cornell（2009）用另一组参数表示等价的加利福尼亚模型。

为了估算P ［IME≤im｜m，r］和P［IMA≤im｜m，r］项，使用了Ambraseys等（1996）的地震动预测方程；因此，要考虑的震级标度是该地震动预测方程的标度。Ambraseys等（1996）使用的是Rjb距离度量，指到震源地表投影的距离（Joyner and Boore，1981）。另一方面，由于图1中的点被看作主震的震中，由Gruppo di Lavoro（2004）给出的式（13）用于得到需要在地震动预测方程中插入的从震中距R转换的Rjb（km）值，其在前面地震危险性积分中用RE或RA表示。

3.2 案例和结果

给定为应用所做的工作假设，基于序列的地震危险性概率分析根据式（10）进行计算。首先的实践执行中，强度测度视为地面基岩的地震动峰值加速度（PGA）。而且，按Yeo和Cornell（2009），余震序列的持续时间（ΔTA）任意视为等同于从主震发生后的90天（Yeo，私人通讯，2013）。

图3a按照不同的地震动峰值加速度阈值的年超越率，比较了基于序列的地震危险性概率分析的结果和使用式（2）由地震危险性概率分析得到的只考虑主震的结果。当然，图3b中也用发生率显示了基于序列的地震危险性概率分析和地震危险性概率分析的相对差异。尽管危险性曲线很接近，但可观察到发生率高达30%的差异。

因为5%阻尼伪谱加速度SA（T）是一般地震工程意义的强度测度，基于序列的地震危险性概率分析也依靠这个强度测度计算，其T（结构周期）在0～2s范围变化。这种进一步分析的结果用均匀危险性谱（UHS）表示，即，频谱纵轴在给定时间框架内都有相同的超越概率，或等效的相同重现周期（如Reiter，1990）。在图4a，将表示普通结构典型生命安全相关设计重现周期475年的均匀危险性谱与其地震危险性概率分析的相应参数作对比。图4b显示分别采用基于序列的地震危险性概率分析和地震危险性概率分析计算的频谱的相对差异。注意，在此情况中，比较依据的是给定重现周期的强度测度（而不是前例中的发生率），发现有高达10%的变化。

这些结果，根据发生率和加速度的变化，与Boyd（2012）得到的结果相差不大，尽管在两个研究和应用实例中存在差异（Boyd，私人通讯，2013）。

4 结论

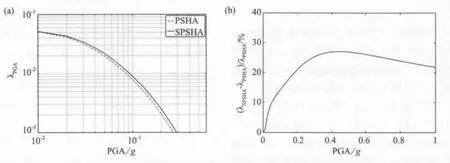
图3 （a）应用实例中用地震动峰值加速度（PGA）表示的地震危险性概率分析（PSHA）和基于序列的地震危险性概率分析（SPSHA）的结果。（b）应用实例中用地震动峰值加速度（PGA）表示的地震危险性概率分析与基于序列的地震危险性概率分析的差异

图4 （a）用475年均匀危险性谱表示的地震危险性概率分析（PSHA）和基于序列的地震危险性概率分析（SPSHA）应用实例结果，即5%阻尼伪谱加速度与震荡周期的关系，其中所有坐标都有相同的10%的50年超越概率。（b）应用实例用475年均匀危险性谱表示的地震危险性概率分析和基于序列的地震危险性概率分析的差异

这篇短文的研究目的在于帮助在地震危险性分析中用地震动强度测度的超越率表示，将大森型余震也纳入主震事件来考虑。重点是对危险性积分在概率上一致形式化，着眼于在地震序列期间至少一次超越强度阈值的事件。

由于地震丛集中的任何地震都可超越所关注结构的临界强度，在超越率的估算中直接扩展包含余震潜在威胁的地震危险性对于基于性能的设计可能有用。

对主震—余震地震序列的地震危险性概率分析基于的是主震发生的均匀伯松过程假设和余震发生的条件非均匀伯松过程。后者依赖于通过修订的大森定律得出的主震特征和主震特征与余震震源区之间的半经验关系。

用解析公式进行基于序列的地震危险性概率分析考虑的是，在给定触发主震震级和位置的情况下，余震的影响（即地震动强度）有条件地与这个丛集之外发生的任何事情无关。

应用实例指的是主震的一般震源区和一般余震序列。对基于序列的地震危险性概率分析结果与经典的地震危险性概率分析结果进行了比较，二者用的是给定强度测度阈值的发生率和给定重现周期的强度测度。结果至少对设置的案例显示，对应475年重现周期的地震动峰值加速度发生率有高达约30%的变化，伪谱加速度值有高达约10%的变化。

相信导出的公式会对地震工程有意义，特别是对长期基于性能的结构设计和评估。

数据与来源

本研究使用的所有数据均来自参考文献中列出的公开出版资料。Toro和Silva（2001）的报告来自 http：／／www.riskeng.com／downloads／scen－ceus－rept（最后访问时间2013年7月）。Gruppo di Lavoro（2004）的报告来自 http：／／zonesismiche.mi.ingv.it／documenti／rapporto－conclusivo.pdf（意大利文，最后访问时间2013年7月）。