MSATSI：结合可靠经典方法的新简化用户处理及可视化工具的应力反演MATLAB软件包

P.Martínez－Garzón G.Kwiatek M.Ickrath M.Bohnhoff

引言

根据地震震源机制估计应力场方向是理解地壳力学以及地震物理现象的一个相关方法。在全球地震学中，法向应力反演（FSI）是研究与大地震发生相关的构造过程的一个较为成熟的技术（如 Hardebeck and Michael，2004；Yoshida et al，2012）。应力场方向的信息也与碳氢化合物和地热资源的开发有关。最大水平应力（σHmax）方向的信息对油藏开发，如钻井和泄露的风险评估（Terakawa et al，2012； Martínez－Garzón et al，2013），至关重要。此外，法向应力反演技术对于在实验室的岩石变形实验框架下的微观尺度上理解破裂物理进程是有用的。

在地震学的实践中，应力张量要么根据地震震源机制反演得到，要么直接根据初动极性得到。大多数成熟的法向应力反演技术有两个主要的假设：

（1）在考虑的岩石范围内，应力场是均匀的。

（2）断层的滑动平行于牵引力的切线方向（Wallace，1951；Bott，1959）。

估计应力场方向是非线性反演问题，可以采用直接求解，也可以采用线性化求解。在求解非线性反演问题时，使用网格搜索法（Gephart and Forsyth，1984；Gephart，1990；Arnold and Townend，2007）或基于采样优化的蒙特卡罗方法（Angelier，1984；Xu，2004）得到一组与震源机制达到最优拟合的应力张量。线性反演策略是通过计算量小、被广泛应用的最小二乘法求得（Michael，1984； Hardebeck and Michael，2006）。

由于反演问题的具体特点，不确定度的评定通常是法向应力反演的必要组成部分。以下专题特别重要：

1.由于不同取向的一组断层能被同一应力状态活化（McKenzie，1969），一个单一的震源机制仅能将应力场方向约束在相应的膨胀象限内。因此，震源机制数据必须包含一定的多样性来约束反演问题的解。

2.反演应力张量时，要明确知道滑动发生的断层面。然而，根据地震双力偶源模型的概念，存在两个可能的断层面：真正的断层面和辅助断层面（Aki and Richards，2002）。当缺乏其他信息时，两个断层面具有相同的可能性。

本文讨论一个程序包，即 MSATSI，它允许法向应力反演（FSI）在MATLAB环境中使用（http：／／www.mathworks.com／products／matlab／；2014年5月查询）。新的算法根据SATSI算法（Hardebeck and Michael，2006）重新设计。在该程序包中，我们采用各种图表示0D～3D的法向应力反演结果，使其可视化。我们采用具有不同特性的数据集对MASTSI进行测试，测试法向应力反演以及0D～3D不同范围输入数据的可视化工具的有效性。这个软件包得到了GNU通用公共许可证（GPL）并对所有用户免费使用。

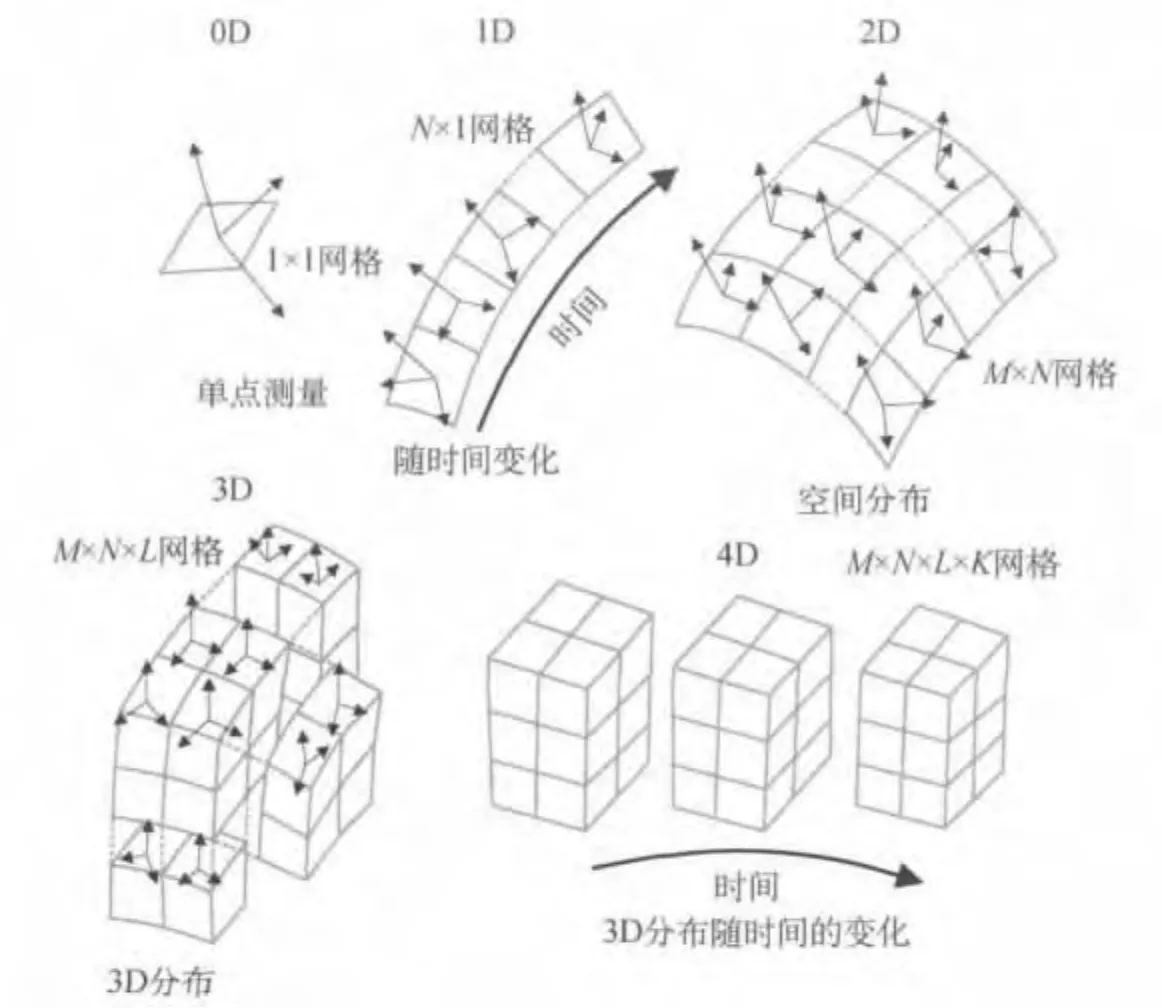
图1 用SATSI和MSATSI进行法向应力反演的可能维度说明。0D为单一的静态应力场。1D为一个坐标分布（如，随时间分布）的一系列应力张量。2D生成在两个坐标变化的应力张量结果图（如：表面分布的应力）。3D为三维应力分布，如应力场的空间分布。4D生成在时间和空间变化的应力张量方向分布

1 SATSI应力反演

自然界中，两个不同应力状态之间的过度一定是连续的。然而，在调查研究应力场方向的分布时，所获得的应力张量解也许取决于输入数据被约束的方式（Hardebeck and Michael，2004；Townend and Zoback，2004）。SATSI算 法 （Hardebeck and Michael，2006）就是为处理此问题而创建的。程序中，输入震源机制在反演之前可被分到按一定维度分布的许多子区（我们称之为网格点）上，维度从0D（一个网格点的单一法向应力反演运行）到1D（应力场随时间变化）再上升到4D（时空分布），4D是把时间作为一个额外的坐标。然后，采用阻尼最小二乘反演同时得到每个网格点的应力张量并进行平滑。由于SATSI的法向应力反演的稳健性，再结合阻尼最小二乘法优化策略（Menke，1989）及良好的计算性能，我们采用了该软件。对于SATSI的完整描述，请参考Hardebeck和 Michael（2006）及 Michael（1984，1987）。

反演提供了3个主应力轴方向和一个反映相对应力大小R值的量（φ）：

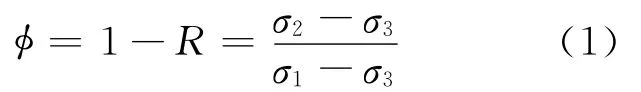
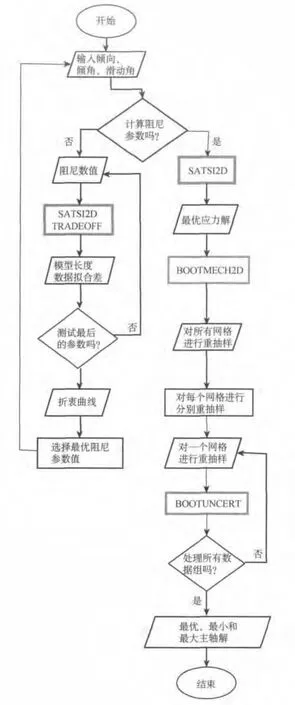
图2 描述SATSI处理工作流程的流程图。灰色的矩形是SATSI软件包中提供的程序

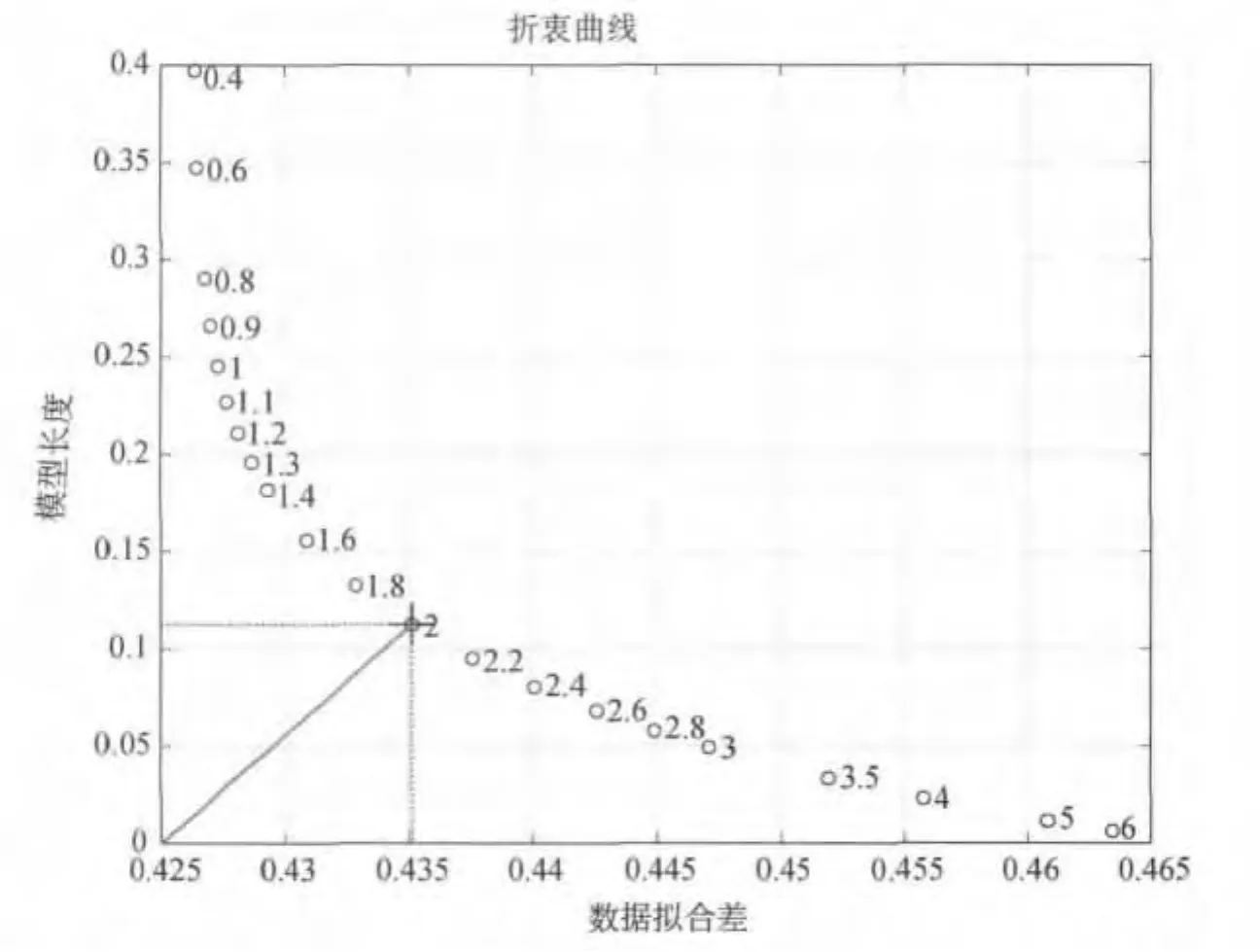
图3 从一组估计的阻尼参数计算的数据拟合差与模型长度的依赖关系（阻尼参数值标在每个点的旁边）。所选择的阻尼参数用十字表示

式中σ1－σ3是从偏应力张量中得到的3个主应力大小的度量。相对应力大小是中间主应力σ2的值更接近于最大压缩轴σ1的大小还是最小压缩主应力轴σ3的大小的度量。采用重采样法进行震源机制数据的输入，从而得到应力轴方向和应力相对大小的不确定性。

图2展示了SATSI的流程图，按照通常叙述忽略了网格点分布的维度数量。然而，事实上对于0D／1D／2D和3D／4D的不同情况，法向应力反演实际调用的程序均不相同。使用SATSI计算应力场方向的最主要步骤如下：

1.定义反演中的最优阻尼参数。该步骤是多次调用子程序satsi＿tradeoff.exe实现的，该步骤给出描述数据拟合差与模型长度相互依赖的函数。综合考虑数据拟合差和模型长度，使其最小化，则得到了这两个值的估计。

2.阻尼法向应力反演采用程序satsi.exe对所有网格点同时进行反演，确定每个网格点的最优应力张量方向和应力相对大小。

3.通过对每个网格点的原始输入数据重取样，多次反演完成不确定性的评定。该步骤通过程序bootmech.exe完成，通过对原始数据随机采样建立新的数据子集代替原来的数据集，并执行法向应力反演确定应力参数。

4.最后，子程序bootuncert.exe在特定的置信区间内选择重取样数据子集。

SATSI程序包的源代码用C程序语言编写。因为程序必须按特定顺序调用（与图2相比较），Hardebeck和 Michael（2006）提供了另外的Perl脚本，实现了半自动化的计算流程。然而，基于程序的工作流程，还可以对不同输入数据类型的均质化和最优化方面进行显著改善，更有效和更便于用户输入输出数据处理，扩展功能。

2 MSATSI程序包

MSATSI由两个程序组成。第一个（msatsi.m）覆盖整个法向应力反演工作流程（与图2比较）。它处理原始SATSI软件包程序之间的数据交换并提供良好的结构输出。第二个（msatsi＿plot.m）是将法向应力反演结果图形化的程序。这个程序能够处理高达3D的法向应力反演解，生成若干不同的图形。

给定法向应力反演的初始参数，并使用MATLAB的特性（属性名—属性值对）及图形输出属性进行设置。在这里，我们论述两个子程序的最重要的特性，其他特性的完整描述可以在程序包的说明书中查到。

2.1 msatsi.m

Msatsi.m程序根据震源机制计算应力方向并提供自助重采样得到的不确定度估计（与图2对照）。相对SATSI，该程序增加或修改了几个方面，最相关的如下：

1.msatsi.m能够运行0D情况下的法向应力反演，也就是说，可计算单一网格点的应力场方向（根据提供的数据计算没有空间和时间变化的静态应力场）。

2.对于任何要处理结果的维度，程序以同样的方式处理常规输入／输出数据。所以，相同的程序能应用于任何维度。

3.mastsi.m从给定震源机制中计算P轴和T轴的分布。这对于直观检查震源机制数据的多样性是否足以进行法向应力反演是有用的。

4.程序可根据输入的数据自动估计合适的阻尼参数，并产生相应的折衷曲线（图3）。需要注意的是，阻尼参数值的微小变化不会对结果产生重大影响。

5.mastsi.m处理由SATSI可执行程序在法向应力反演和输入／输出中出现的错误。

6.为了便于用户，所有相关的法向应力反演结果聚集在一起输出，也包括与重采样数据相关的、在选择的置信区间含有的附加信息。

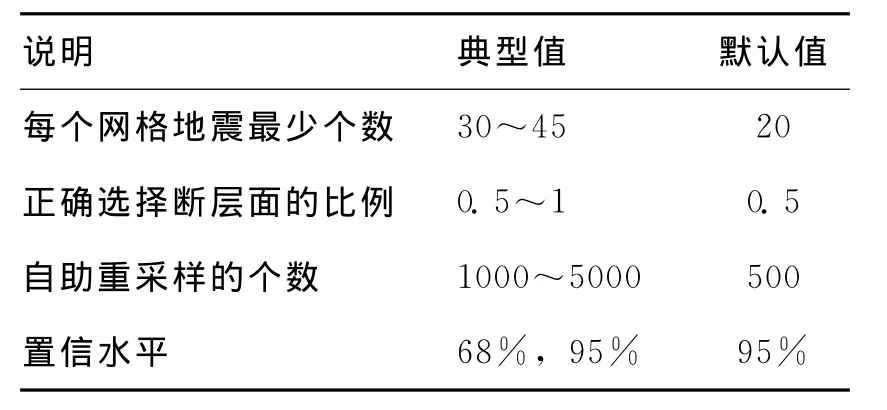
表1 用MSATSI控制法向应力反演的默认值及典型值

表1列出了控制法向应力反演程序的最重要参数及建议的区间和默认参数值。每个网格点地震事件的最小数目是约束法向应力反演所必需的（见引言）。如果没有达到最小数目，则不会进行相应网格点的反演。从地震数据中正确地选择断层面的比例F处理断层面的模糊性问题。使用MSATSI，用户可以明确指定每个输入断层面为真实断层面的概率。这是非常有用的，例如，如果输入的断层面来自于直接地质测量（在这种情况下F＝1）。重采样的迭代次数对于不确定度评定是很重要的。经验数值大约为输入数据的数量的20倍（Efron and Tibshirani，1986）。最后，应该给出不确定度的预想置信水平，通常使用的默认值为95%。

2.2 msatsi＿plot.m

msatsi＿plot程序的目的是提供各种各样的msatsi.m计算应力场反演结果的图形表示。该程序能够显示所有0D～3D应力反演的输出数据。该程序也能给出法向应力反演的维度减少的结果的表示，即所谓的切片图。例如，一个3D分布图可以沿任意坐标方向切片成为2D图。该特性极大地简化了法向应力反演结果的分析。

该程序包括5个基本类型的图。通常情况下，这些图显示主应力方向、应力相对大小（R）及它们的不确定度。不确定度可以表示为置信区间或者散乱分布的自助重取样解。能够得到的5种图如下：

1.球面投影网图。适合用来表示0D～1D的法向应力反演结果（如仅一个法向应力反演结果／暂时变化）。采用球面投影网及下半球等面积／等角度投影法绘制主应力轴的方向（图4a），每个网格点的R值绘制在另外的图中。

2.剖面图。适合表示1D的法向应力反演结果。该图是由3部分组成，分别展示主应力轴的走向和倾角的变化以及每个网格点R值的变化（图4b）。

3.球面投影图（stereomap）。适合2D法向应力反演结果可视化（例如：平面分布）。每个网格点的主应力轴方向采用球面投影网绘制在一幅图中（图5b）。R值的2D分布展示在另外的图中。

4.WSM（全球应力图）。产生与全球应力图项目（Heidbach et al，2010）兼容的2D图形。该图根据适用于最优应力反演解、由Lund和Townend（2007）提出的最大水平应力估计校正的相应应力断层体系分类判据（Zoback，1992）展示出最大水平应力轴方向（图5a）。该估计采用主代码 masti＿plot.m内部子程序SH.m（公用可得到）运行。

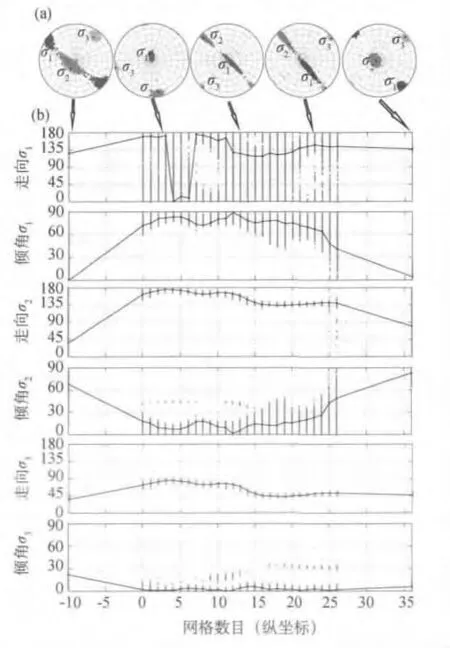
图4 与伊兹米特地震相关的应力场随时间变化。（a）特定时间周期上的结果表示（球面投影网）。（黑色十字为最优解；灰色点为95%的置信区间）。（b）应力场方向随时间的变化（剖面图）。分别绘出了σ1、σ2和σ3的走向及倾角的最优解。置信界限95%用灰点标绘

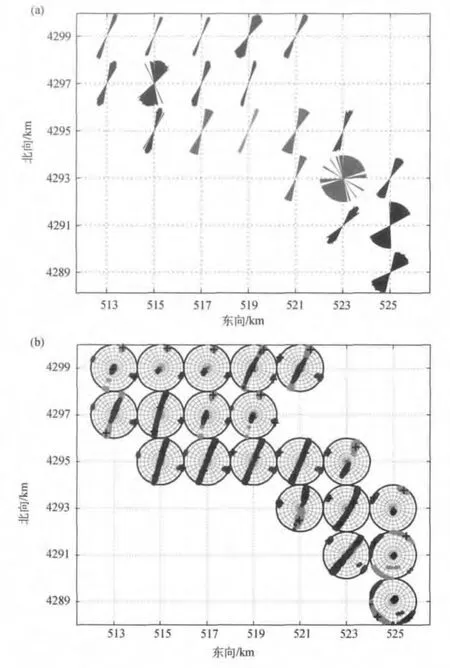
图5 盖瑟地区应力场方向的平面分布。（a）用全球应力图（WSM）的结果。每个网格点都绘出最大水平应力［根据最优解，红色（原图为彩色图——译注）表示正断层作用体系，绿色表示走滑断层体系，灰色表示斜滑断层体系］。（b）用球面投影图表示的结果。红色表示σ1，绿色表示σ2，蓝色表示σ3，黑色十字表示最优解，彩色点表示95%的置信区间。图中坐标采用全球通用横轴墨卡托投影（UTM）坐标表示

5.三维立体图（stereovolume）。适合表示3D法向应力反演结果。图中，主应力方向根据走向和倾角绘制成3D表示。该思路与球面投影图类似，但扩展到了3D（图6）。

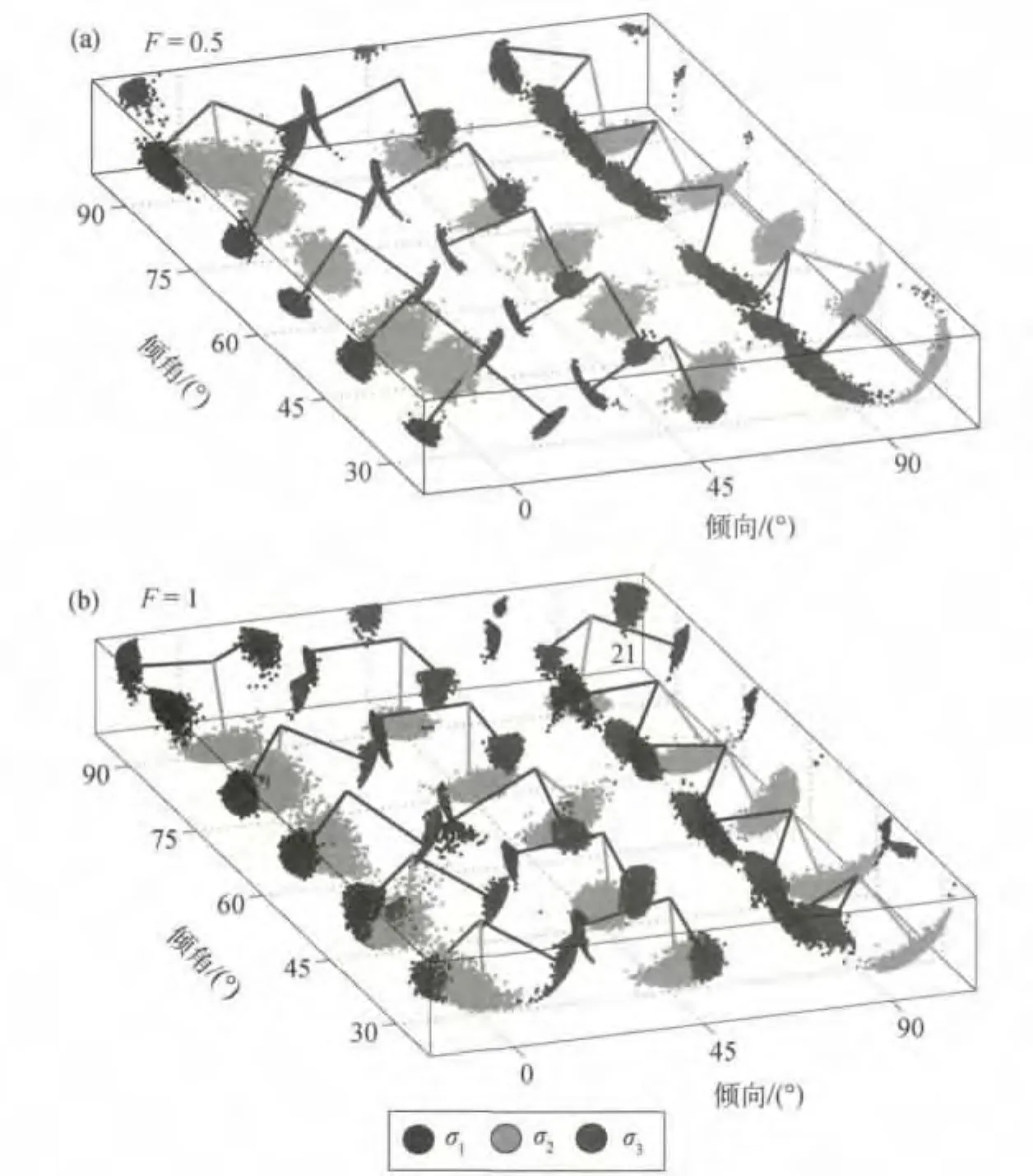
图6 用三维立体图并仅选择λ＝0°的数据对合成数据子集进行法向应力反演（FSI）的结果。采用了两个正确选择断层面的比例进行尝试。红色（原图为彩色图——译注）表示σ1，绿色表示σ2，蓝色表示σ3，实线表示最优解。用相同的对应颜色绘制不确定的点

绘出的图可以根据用户的偏爱采用30多个属性对用户参数设置进行修改来调整图形。在MSATSI文档中提供了完整的属性列表，并提供了大量代码例子，还有将得到的结果图形化表示的详细说明。

2.3 MSATSI软件包的内容

MSATSI软件包由以下部分组成：

1.根目录包括msatsi.m和msatsi＿plot.m，还有在Microsoft Windows平台下改进并编译的SATSI可执行文件。

2.／bin文件夹含有为Windows、Linux和Mac平台编辑而改进的SATSI可执行文件。

3.／example目录包含 MSATSI软件包的使用说明，覆盖了本文给出的1D到3D的例子。0D的例子给出的另一个实例研究不再这里描述。

4.／src包括根据原始SATSI软件包修改的C代码，也提供了在不同的平台打包编译指令。

3 MSATSI应用的不同案例

3.1 北安纳托利亚断层带应力场方向随时间的变化（1D）

北安纳托利亚断层带是安纳托利亚板块与欧亚大陆板块的边界，同时也是世界上转换断层研究最为成熟的地区之一。它从安纳托利亚东部延伸到北爱琴海，长度超过1 200km。

我们的研究旨在更好地理解应力场的局部旋转是否可以作为一个指标来描述在地震周期内沿单一断层段的地震构造背景。为达到此目的，我们应用MSATSI调查与土耳其西北部北安纳托利亚断层带上1999年伊兹米特MW7.4地震相关（Bohnhoff et al，2006；Ickrath et al，2014）的应力场随时间的变化。

这里使用的数据涵盖了1999年伊兹米特MW7.4地震震前、余震序列以及震后的数据。该地震破裂的140km长的断层段上显示了右旋走滑断层机制。我们编辑了根据不同地方及区域地震台网记录确定的（Bulut et al，2007；Görgün et al，2010；Örgülü，2011）、分布在北安纳托利亚断层伊兹米特段震级在0.8到7.4之间的989个地震事件的断层面解。地震活动时间跨距从1943年到2007年。

将输入数据集划分为不同时间段：伊兹米特地震前时间段、伊兹米特余震的两个月和震后时间段。余震时间段包含更多的震源机制，又进一步按照伊兹米特地震的分段，用20个重叠事件的包含70个事件的移动时间窗进行了划分。用MSATSI反演了子集的应力张量。我们使用有阻尼的法向应力反演，对原始数据集进行2 000次自助重采样。不确定度假定为95%置信水平的置信区间。

图4展示了用球面投影网和剖面图绘制的法向应力反演的结果。我们发现主应力轴方向随时间有明显变化。伊兹米特地震之前和之后3个月地震序列的区域应力场为约N130°E走向的最大水平主应力（σ1）的稳定走滑体系，这与右旋东西走向的北安纳托利亚断层一致。相对而言，同震早期被NE—SW向拉张的正断层体系控制。这些结果的详细描述和解释参见Ickrath等（2014）。

3.2 盖瑟地热场的应力场方向平面分布（2D）

加利福尼亚北部的盖瑟（TG）地热场是世界上最大的产热地区，覆盖了280km2的面积，拥有约70个回注井和350个蒸汽井。在2007至2012年间，记录到由于注水和蒸汽开采而产生的16 800多次M≥1的微震活动（Martínez－Garzón et al，2013）。

我们通过北加利福尼亚地震数据中心，得到了分布在整个地热场的4 859个地震震源机制（MD1～4.5），以此来分析蓄水深度面上的应力场分布（平均在2到2.5km之间）。将盖瑟（20km×14km）划分为2km×2km面积的网格。对多于30个微震机制的网格进行2D阻尼法向应力反演。不确定度的评估是由2 000次输入数据的重采样完成的，其置信度设置为95%。

图5a展示了使用 WSM（全球应力图）绘制的每次法向应力反演的最大水平应力方向。对于大多数网格点，σHmax的方向与加利福尼亚北部区域应力场（Provost and Houston，2003）一致。虽然在蓄水区的局部应力状态通常为正断或张扭性的，但坐标为东向515km、北向4 295km的网格点符合走滑标准。

图5b显示的是用球面投影图绘制的主应力轴分布图。本例中重取样得到的结果占了较大面积（如，北向4 295km得到的σ1和σ2应力轴），采用重取样选项给出的置信区间表示可能提供了更真实的表示。对于图5a中显示为走滑的网格点，我们看到σ1和σ2倾角的不确定度很大。连同较低的R值，这个事实说明这些轴的应力大小是相似的。该区域南部（东向525km的反演结果），自助重采样结果的σ2和σ3轴走向具有较大范围，表明这些轴的应力值相对于σ1较小，因此，σHmax走向的不确定度更大。这些观测得到了每个网格点R值的分布的支持。

从全局来看，盖瑟地热场区可能与蓄水区的体积收缩导致蓄水区内水平应力的减小相关。然而，在一些热田开发相对较新的特定区域观察到正应力体系，或许与拉张新鲜破裂的增多增加了地热系统蓄水区的渗透性有关。

3.3 合成检验（3D）

我们以研究断层几何如何影响最终法向应力反演结果并检查3D程序的正确表现为目标，生成了一个合成震源机制目录。我们通过改变3个断层面参数：倾向φ＝ ｛0°，45°，90°｝、倾角δ＝ ｛30°，45°，60°，75°，90°｝和滑动角λ＝ ｛－90°，－45°，0°，45°，90°｝来生成一个3D的格状网（3×5×5）。所以，这些参数的不同组合覆盖了所有的断层模式，从纯走滑经过斜滑再到纯逆断或正断。每个网格点产生了100个震源机制。对于序号为i，j，k的网格点第m个随机产生的断层面可以描述为断层面参数的组合 ｛N （φi，σφ），N （δj，σδ），N （λk，σk）｝（m），这里 N（·）为根据平均值等于给定倾向、倾角和滑动角值的正态分布抽取的随机数，σφ、σδ和σλ是震源机制抽样的标准差。

图7 展示倾向φ＝0°的合成数据检验结果的球面投影图。该图采用切片属性绘制，颜色代码与图5描述相同

在这项检验中，所有标准差均设置为σφ＝σδ＝σλ＝35°。选择这个数是为了确保数据中正确的可变性。其他采用均匀分布的合成数据检验表明，为合理约束应力张量，断层面解必须有30°的最小可变性（Hardebeck and Hauksson，2001）。结果是，断层面解的张轴T和压轴P在最优取向周围震荡。所以，最大压缩主应力轴（σ1）和最小压缩主应力轴（σ3）的取向应该分别对应于P轴和T轴的平均取向。这在大多数地震发生在相对于应力场的最优取向断层的例子中均能看到。

在本次分析中，我们没有使用阻尼方案，因为我们不想得到的受周围网格点影响的结果。不确定度的估计通过2 000次初始输入数据的自助重采样计算。

虽然我们先验地知道这里指定的断层面是适宜反演的，但是，我们对正确地选择断层面的比例尝试了两个值。在第一种情况下，我们假设所有指定断层面是正确的，这与反演地质擦痕（F＝1）的情况相似；而在第二种情况下，我们从两种可能选项中随机选择其一（F＝0.5）。当不能获得额外信息时，这是地震学中最普通的情况。所以，我们可以检验随机选择断层面得到的解有怎样的不同。

对于两个参数的反演实例的可视化采用三维立体图绘制，并可从本文的电子补充材料获得。为了方便可视化，图6展示了检验用的两个F值和滑动角λ＝0°的纯走滑情况的应力反演结果。两种情况得到的结果极其相似，说明随机选择断层面也会提供有效解。然而，对于F＝0.5的情况，水平轴引入了一定斜度，因为反演能够很好区分某些成对坐标轴，在这种情况下，不确定度与F＝1的情况相比略有减小。

正如所料，控制应力状态的最不重要的参数是倾向，因为该参数沿走向围绕3个主应力轴的最优解系统地旋转。

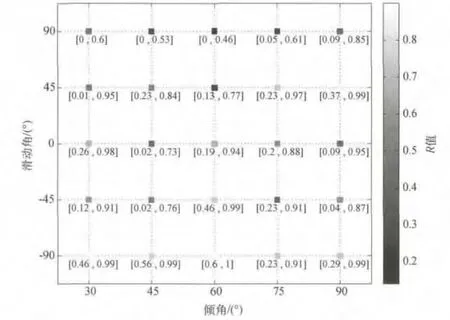
图8 与图7球面投影图对应的R值分布。每个网格点的最优解用颜色编码显示，不确定度的区间标在最优解的下方

一旦正确断层面的比例变化确定且倾向也经过检验，为了更容易地显示其他两个参数，我们去除倾向将初始的3D网格降至2D。图7展示了φ＝0°和F＝1的数据切片。根据Anderson（1951）定义的3个主要断层体系及过渡状态均清晰可见。正如所预期，纯正断层作用（σ1垂直）在δ＝45°，λ＝90°出现；纯走滑断层（σ2垂直）机制在δ＝90°，λ＝0°出现；纯逆冲断层（σ3垂直）在δ＝45°，λ＝－90°出现。对于相同值的滑动角，倾角的变化将会引起应力轴取向产生一定的倾斜度变化，这将使最大倾角增加。然而，确定应力体系的主要影响为滑动角。

该切片中对应于反演结果的R值分布绘于图8。我们注意到应力体系越接近纯正断层，R值越趋近于1；应力体系越接近纯逆断层，R值越趋近于0。这可以用纯断层滑动（倾斜度更小）情况下水平应力量值相比于垂直应力量值更相似的观测事实来解释。这种差别对于F＝1的情况更加明显（见电子补充材料）。

4 结论

MSATSI软件包基于SATSI算法（Hardebeck and Michael，2006）在 MATLAB环境下可以进行完全的应力反演。在MSATSI内部，整个法向应力反演程序得到改善，程序自动执行，并且更加用户友好。第二个程序对适当可视化的应力张量反演结果及其置信区间提供了整套法向应力反演输出数据的图形表示。MSATSI程序包已得到通用公共许可证并可免费获得。

MASTSI已用于不同的数据集，在各种不同环境下检验了所开发程序的性能。对于沿土耳其东北部北安纳托利亚断层的天然地震活动和在加利福尼亚盖瑟地热区诱发地震活动的分析，反演结果与其他研究和／或实地考察相一致，表明MSATSI的性能是正确的。此外，我们还通过合成震源机制数据验证了3D的法向应力反演。

在众多已经存在的法向应力反演软件包中，MSATSI有使大部分潜在合理环境相统一的优势。它不但可以使用不同网格点分析应力场取向的变化，也可能对输入数据进行单一的应力反演。另外，这个程序可以阻尼（平滑）地从天然观测中得到更真实的结果，但对想要的情况也可能无效（如本文的合成例子）。最后我们说明，无论输入地震的大小或性质如何，该方法均能正确表现。