基于组合核函数KPCA的人脸识别研究

赵剑华，王顺芳，张飞龙

（云南大学 信息学院，云南 昆明650091）

0 引 言

基于核主成分分析 （KPCA）［1］的人脸识别方法能够提取出人脸信息中PCA［2］（主成分分析）等线性分析方法不能够提取但有利于人脸识别的高维非线性信息，表现出优越的分类性能，是机器学习和模式识别领域的研究热点。现有的KPCA人脸识别方法大多是基于单核函数的研究，具有很大的局限性。鉴于不同的单核函数具有不同的特性并对应着不同的高维特征空间，拟合理组合几个不同的单核函数形成新的组合核函数［3］，在一定意义上综合各单核的优点，提高识别的整体性能。具体将学习能力强的高斯核函数分别与泛化能力强的多项式核函数和线性核函数组合，形成新的核函数应用于KPCA人脸识别。通过序列实验证明该组合核函数兼有良好的学习能力和泛化能力，识别效果和整体性能比基于单核函数的KPCA方法和PCA方法优越。

1 基于KPCA的人脸识别方法

基于KPCA［1］的人脸识别方法是通过一个非线性映射，将训练集的数据隐式的从一个低维的特征空间映射到一个高维的特征空间中，并且在新的高维特征空间构造了一个最优分类面，从而解决线性不可分数据的提取和分析等问题。该方法是在一个相对较小的高维线性子空间中进行运算，避免了在整个高维空间中进行大量复杂、繁琐的运算，它的维数最多等于样本的数量；同时映射过程通过核函数来实现，不需要知道非线性映射的确切表达式。

设输入训练样本数据Xk（k ＝1，2，……N）被映射为（Xk）。

即：Xk→（Xk），且变换后的数据已经被中心化，即满足。则变换后的训练样本（Xk）的总体散步矩阵C 为

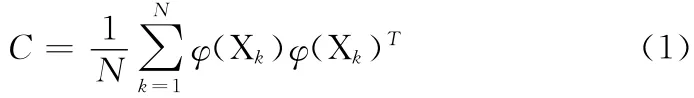
求解特征方程

其中V 为特征向量。根据再生核理论［4］：特征向量V 一定位于由（X1）（X2）…（XN）组成的空间内，即V 可以由（X1）（X2）…（XN）来表示即

其中α1、α2、…αN为常数。

定义一个N×N 且满足Mercer条件的矩阵K［5］

K 称为核矩阵，将式 （1）、式 （3）、式 （4）代入 （2）中得

这样求式 （2）特征向量V 的问题就转换为求解式 （5）的特征向量α。通过求解特征方程 （5）得到一组非零特征值λi以及对应的满足归一化条件：λi（αi，αi）＝1的特征向量αi（i＝1，2，…N′，N′≤N）。根据式 （3）得到特征空间上的投影主分量Vj（j＝1，2，…，N），设X 为一测试样本，则其在Vj上的投影为

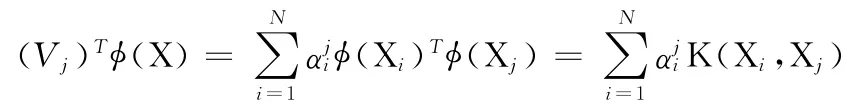
这样就可以得出原始图像经过变换后的投影特征向量，在求解过程中始终不需要知道映射函数（X）的确切表达式，而只需要知道核函数K（x，y）＝（（x）T（y））的表达式即可。核变换并不能保证，因此要对变换后得到的核矩阵K 进行中心化

2 多核函数组合的分析方法

每一类核函数都有自身的特性，有自己的适用范围，对应着不同的映射和高维特征空间，同时不同的核函数会产生不同的分类效果［6］。因而根据核函数对数据的作用范围将核函数大体分为两类：全局核函数和局部核函数［7］。目前常用的核函数有高斯核函数、多项式核函数、线性核函数、Sigmoid核函数 （Sigmoid核函数的适用范围比较小，它只在某些特殊核参数值的条件下才满足Mercer条件［8］），像高斯核函数这个类型的径向基核函数其径向作用范围是由核函数的宽度参数来控制的它只允许相近的数据点对核函数的值产生影响，插值能力很强，比较善于提取样本的局部信息，具有很强的学习能力；而多项式这一类型的核函数却允许相距较远的数据点都可以对核函数的值产生影响，插值能力相对较弱，但比较善于提取样本的全局特性，具有很强的泛化能力。

首先介绍几个定理［9，10］：

定理1 K（θ，θ′）是Rl×Rl的核，若θ（X）是从XRn到Rl的映射，则K（X，Z）＝K（θ（X），θ（Z））是Rn×Rn上 的核。特别的，若n阶矩阵B是半正定的，则K（x，z）＝xTBz是Rn×Rn的核。

定理2 设K1和K2是X×X 上的核，且XRn，则下面的函数均是核

根据定理1和定理2分析，构造形如

的函数组合依然还是核函数。所以，如果适当选择具有不同性质的单核函数，根据式 （6）将学习能力较强的局部核函数和泛化能力较强的全局核函数进行合理的组合，组合后的核函数将同时汲取局部核函数和全局核函数的优点，使组合核函数整体的学习、泛化性能得到大大提升，将其应用于人脸识别方法的讨论、研究就能保证在进行图像特征提取时既能保留图像的整体信息，又能突出不同图像类别的局特征，其性能将优于基于单核函数的KPCA 及PCA 方法。

基于多核函数组合的KPCA 人脸识别方法的基本步骤：

（1）输入训练图像集Xk（k＝1，2，……，N）

（2）计算核矩阵：K

（3）求中心化核矩阵：K′

（4）计算K′的特征值λ和特征向量α。

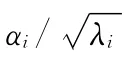
（6）对计算所得的特征值进行降序排列。

（7）根据累积贡献率提取前i个特征值及其对应的前i个特征向量，构成训练图像集的主成分方向。（前i个特征值的贡献率一般占所有特征值总和的80%以上，或根据具体问题来定）。

（8）将训练图像集投影到第 （7）步求得的主成分方向上，提取出训练图像的特征脸集。

（9）输入测试图像并进行相应的核变换得到核矩阵，然后将该核矩阵投影到 （7）步求得的主成分方向上得到相应测试图像的特征脸集，并将其与训练图像的特征脸集进行比较分类。

3 实验及结果分析

本文分别采用ORL标准人脸库［11］和YALE 人脸库［12］进行实验，其中ORL 标准人脸库由40个人在不同的拍摄时间拍摄的有姿态、角度、尺度、表情和眼睛等变化的图像，每个人的人脸由10幅112×92的图像组成。实验首先选取每个人的5张图像作为训练样本，然后随机选取其它5幅图像作为测试样本。

为了验证本文方法的识别效果，将分别比较PCA、单核函数KPCA、多核函数组合KPCA 方法在两个人脸数据库中的识别效率。其中单核函数采用的是高斯核函数式（7）；而多核函数组合KPCA 使用式 （6）组合，且组合核函数为：

组合一：式 （7）和式 （8）（多项式核函数）组合，组合二：式 （7）和式 （9）（线性核函数）组合

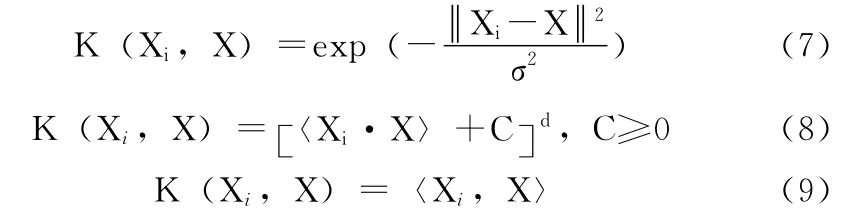
核函数的参数变化会隐式地改变从输入空间到特征空间的映射，进而对特征空间的性质产生影响，最终改变各种核函数的性能，即核函数与非线性映射不是一一对应的，核函数参数一旦改变它所对应的非线性映射和高维特征空间就会发生改变。然而核函数参数的选择还没有比较好的固定取值方法。在实验中用到的核函数涉及的参数比较多，本实验通过先确定单核函数KPCA 的近似最优参数，再将其作为一个参考值以选取组合核函数KPCA 中的参数。实验结果如图1和图2所示。

图1 ORL数据库实验结果

图2 Yale人脸数据库实验结果

实验结果中还发现组合核函数中的组合系数a，b 数值差别很大，说明高斯核函数和多项式核函数对组合核函数的贡献有很大不同。主要原因在于人脸识别是一个比较复杂的过程既要考虑人脸的全局特征，但更主要的是考虑其局部特征，即学习出每个人脸区别于其他人脸的局部特征而不是共性特征，高斯核函数具有很强的局部学习能力，其在组合核函数中对局部信息的学习方面发挥着重要的作用，其权值也相对较大。但也不能忽略权重较小的单核函数的作用，组合后的核函数是一个有机的整体，每一个单核函数在组合核函数整体中都发挥着不可缺少的作用。一般而言，选择合适的单核函数是构造新核函数的关键问题，充分考虑各单核函数的性能组合后的核函数才会更完整，更全面。

实验还研究了两个不同组合核函数的时间效率，在其它条件相同情况下，测试组合一和组合二在不同累积贡献率下的运行时间，结果见表1和表2。

表1和表2的实验结果表明在相同的条件下组合二运行花费的时间比组合一少，其时间效率要比组合一要高。原因是组合二的核函数所涉及的参数比组合一要少，其函数模型要比组合一的函数模型要简单。这也从另一个方面证明了单核函数的选择是构造新核函数的关键。核函数参数的数量会直接影响到函数模型的复杂程度，从而影响到算法的效率。

表1 ORL人脸数据库实验结果

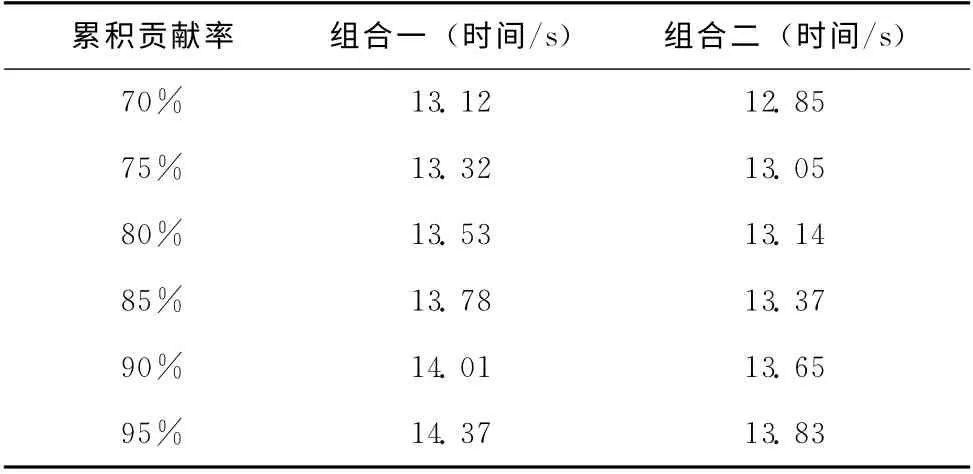
表2 YALE人脸数据库实验结果

为了研究单个核函数与组合核函数参数间的关系，通过使用相同核参数取值 （σ2取值）的情况下实验基于单核函数的KPCA 和基于组合核函数的KPCA 方法的识别率来分析单个核函数的参数取值和该对应的核参数在组合函数中的取值之间的关系，结果见表3。

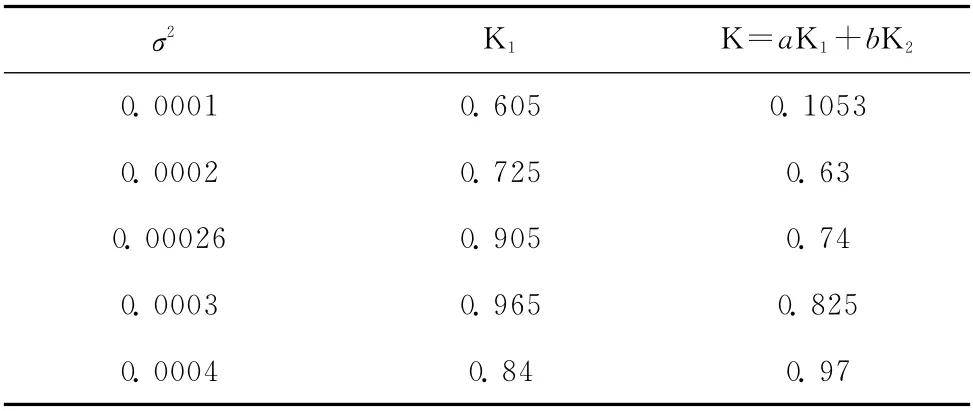
表3 相同参数值下单核和组合核的识别率比较

表3表示综合了核函数参数一般取值情况的条件下，核参数σ2取一些比较有代表性的参数值情况下单核函数K1（高斯核函数）和组合核函数 （高斯核函数 （K1）和线性核函数组合 （K2）组合）的识别率。由实验结果所示同一个核参数在某一取值下使单核函数取得了很高的识别效果，但组合核函数产生的识别效果却很低；而有的核参数值使得组合核函数取得很高的识别效果，但却使得单核核函数发挥的性能一般。说明在实际应用中不能直接将单核函数的参数值直接应用到组合核函数中，两者间对应参数的取值没有必然的联系。而且由实验结果可以看出核函数对于参数的选择非常敏感，核参数一点点的改变会使结果产生很大的改变。因此，组合核函数参数的选择和确定也是基于组合核方法的机器学习和模式识别的核心，在进行单核函数组合时，单核函数参数的取值只能作为组合核函数参数选择的一个参考值，不能直接将单核函数的参数值应用在组合核函数中。

4 结束语

由于每一个单核函数都有自己的特性和最佳的适用范围，不能同时具备良好的全局性和局部性。因而，通过每个单核函数所提取的数据特征的侧重面也不一样，利用单核函数性质间的互补特性，通过将多个具有不同特性的单核函数合理的组合起来分析问题，组合形成的核函数将兼备各个单核函数的特性，并使其整体性能进一步提升，从而组合后的核函数能将问题中不同侧面的特征都提取出来，达到了比单核函数分析问题更全面，更完整的效果。

［1］Hofmann T，Scholkopf B，Smola A J.Kernel methods in machine learning［J］.Annals of Statistics，2008，36 （3）：1171－1220.

［2］Zhuang J，Tsang I W，Hoi S C H.SimpleNPKL：Simple nonparametric kernel learning ［C］／／Proceedings of Interational Conference on Machine Learning，2009.

［3］Gonen M，Alpaydin E.Localized multiple kernel learning［C］／／Proceedings of International Conference on Machine Learning，2008：352－359.

［4］Hoi S C H，Jin R.Active kernel learning［C］／／Proceedings of International Conference on Machine Learning，2008：400－407.

［5］Ying Y，Campbell C，Girolami M.Analysis of SVM with indefinite kernels［C］／／Advances in Neural Information Processing Systems，2010.

［6］Li F，Fu Y，Dai Y H，et al.Kernel learning by unconstrained optimization［C］／／Proceedings of International Conference on Artificial Intelligence and Statistics，2009.

［7］Sonnenburg S，Ratsch G，Schafer C.A general and efficient multiple kernel learning algorithm ［C］／／Advances in Neural Information Processing Systems，2006.

［8］Gonen M，Alpaydin E.Localized multiple kernel learning［C］／／Proceedings of International Conference on Machine Learning，2008：352－359.

［9］Sonnenburg S，Ratsch G，Schafer C，et al.Large scale multiple kernel learning ［J］.Journal of Machine Learning Research，2006 （7）：1531－1565.

［10］Varma M，Babu B R.More generality in efficient multiple kernel learning［C］／／Proceedings of Interational Conference on Machine Learning，2009.

［11］Xu Z，Jin R，King I，et al.An extended level method for effi－cient multiple kernel learning［C］／／Advances in Neural Information Processing Systems，2008：1825－1832.

［12］Vedaldi A，Gulshan V，Varma M，et al.Multiple kernels for object detection ［C］／／Proceedings of IEEE International Conference on Computer Vision，2009.